Математика для блондинок
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
четверг, 14 марта 2013 г.
Куб и угол между прямыми
Сейчас решим задачу про куб и угол между прямыми. Задача звучит так:
Точка Е – середина ребра АА1 куба ABCDA1B1C1D1. Найдите угол между прямыми DE и BD1.
Для начала нужно соорудить конструкцию куба и разукрасить её буквами обозначений. Затем попробуем разобраться, чего надобно этим старцам от математики. Рисуем куб и прямые линии.
Получилось, что одна прямая линия совпадает с диагональю куба, вторая прямая линия проходит через боковую грань куба. Математики такие лини называют скрещивающиеся прямые. Угол между скрещивающимися прямыми определяется (не в смысле математическое определение типа “бла-бла-бла”, а когда конкретное дело делается) как угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым. Это не я такой умный, это у меня книжка умная есть, там и вычитал.
Возьмем ту прямую, которая на боковой грани и проведем параллельную ей прямую линию, проходящую через вершину D1. В этом случае мы получили две пересекающиеся прямые, для которых уже можно определить угол.
| Скрещивающиеся и пересекающиеся прямые |
Для определения угла нам нужны размеры куба. Без этого математика бессильна. Поскольку, по условию задачи, размеры куба нам не заданы, мы можем сами выбрать любой, благо все три размера у куба одинаковы. Примем длину ребра нашего куба за единицу. Получился куб в собственном соку, то есть в собственных единицах измерения. Весь этот математический фокус заключается в том, что угол между заданными нам прямыми совершенно не зависит от размеров куба. И в большом кубе, и в маленьком кубике углы между этими прямыми будут одинаковы.
Дальше всё просто, как в реанимации. Назначаем пациенту, то есть кубу:
1. Две теоремы Пифагора для двухмерного пространства.
2. Одну теорему Пифагора для трехмерного пространства.
3. Одну теорему косинусов.
4. Одну таблицу косинусов.
Теперь разберемся, к каким местам на теле куба всё это нужно прикладывать.
| Два прямоугольных треугольника, диагональ куба, искомый угол в треугольнике |
Рассуждаем от конца к началу. По таблице косинусов мы можем найти значение угла в градусах. Значение косинуса угла можно найти по теореме косинусов, если знать размеры сторон синенького треугольника из рисунка выше. По теореме Пифагора для трехмерного пространства мы можем найти диагональ куба – это одна из сторон треугольника. Две другие стороны треугольника можно найти на гранях куба по обычной (двухмерной) теореме Пифагора. А вот для применения теоремы Пифагора нам необходимы числовые размеры куба. Ведь просто слово “ребро” во вторую степень возвести не возможно. Вот для этого мы и приняли в самом начале размер ребра равным единице.
Мы проутюжили наше решение от начала к концу и от конца к началу. Лично у меня оно где-то по середине и срослось, на теореме Пифагора. Что бы там не утверждали наши современные математики, а математических инструментов мощнее тригонометрии и теоремы Пифагора они так и не создали.
Для полного счастья нам нужно ещё рассмотреть теорему косинусов. Ведь тупо записать её могут многие, а вот применять на практике этот калейдоскоп символов нужно ещё уметь. Посмотрите, как буковки в формулах переливаются! Это и есть первозданная красота математики.
Что такое математическая функция арккосинус? Это очень умное выражение, которым нас пугают математики. А фактически это наша голова и таблица косинусов перед глазами. Или специальная кнопочка на калькуляторе. Только вместо команды “Бобик, фас!” ( косинус – найти число по значению угла), нужно выполнять команду “Фас, покусай Бобика!” (арккосинус – найти значение угла по числовому значению косинуса).
Пусть у нас неизвестный угол будет по кличке “гамма”, а диагональку куба мы обзовем “а”. Отрезок прямой, что расположен на грани куба прямо перед нами, будет именоваться “с”, а на грани слева – “b”. Вот теперь можно погонять циферки и получить числовое решение задачи.
Угол между скрещивающимися прямыми : определение, примеры нахождения
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.

В трехмерном пространстве имеются скрещивающиеся прямые a и b . Проведем прямые а 1 и b 1 параллельные скрещивающимся a и b . Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b 1 являются пересекающимися прямыми.
Обозначим угол между a 1 и b 1 равным значению α . Построение прямых a 2 и b 2 параллельно скрещивающимися относительно a и b в точке М 2 отличной от М 1 приводит к тому, что значение угла между ними обозначим как α . То есть угол между прямыми a 1 и b 1 равен углу между a 2 и b 2 . В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М 1 и М 2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.

Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат О х у z . Имеется задача, в которой необходимой найти угол α , образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M , что дает понять, через нее проходят прямые a 1 и b 1 , которые параллельны скрещивающимся a и b . Угол α , образованными прямыми a и b , из этого определения получится равным пересекающимся a 1 и b 1 .
Для нахождения искомого угла между a 1 и b 1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a 1 и b 1 .
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) .
Векторы a → и b → имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α = a r c cos a → , b → a → · b → = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 , а a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α = a → , b → a → · b → = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 .
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α = 1 – cos 2 α .
Найти угол между скрещивающимися прямыми a и b , которые заданы уравнениями x 2 = y – 4 0 = z + 1 – 3 и x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R и определяются в системе координат О х у z .
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a → = ( 2 , 0 , – 3 ) является направляющим вектором прямой x 2 = y – 4 0 = z + 1 – 3 . При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b → = ( 1 , – 1 , 4 ) является направляющим вектором для прямой вида x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R .
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 = a r c cos 2 · 1 + 0 · ( – 1 ) + ( – 3 ) · 4 2 2 + 0 2 + ( – 3 ) 2 · 1 2 + ( – 1 ) 2 + 4 2 = = a r c cos 10 13 · 18 = a r c cos 10 3 26
Ответ: угол между скрещивающимися прямыми равен a r c cos 10 3 26 .
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра A D и В С , принадлежащие пирамиде A B C D , с известными вершинами с координатами A ( 0 , 0 , – 1 ) , B ( 5 , 7 , – 5 ) , C ( 3 , 7 , – 5 ) , D ( 1 , 3 , 1 ) .
A D → и B C → являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что A D → = ( 1 – 0 , 3 – 0 , 1 – ( – 1 ) ) ⇔ A D → = ( 1 , 3 , 2 ) B C → = ( 3 – 5 , 7 – 7 , – 5 – ( – 3 ) ) ⇔ B C → = ( – 2 , 0 , – 2 )
Из формулы cos α = a r c cos A D → , B C → A D → · B C → находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α = 1 · ( – 2 ) + 3 · 0 + 2 · ( – 2 ) 1 2 + 3 2 + 2 2 · ( – 2 ) 2 + 0 2 + ( – 2 ) 2 = 6 14 · 8 = 3 2 7
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α = 1 – cos 2 α = 1 – 3 2 7 2 = 19 2 7 .
Ответ: sin α = 19 2 7 , cos α = 3 2 7 .
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
Имеется прямоугольный параллелепипед A B C D A 1 B 1 C 1 D 1 со сторонами А В = 3 , А D = 2 и A A 1 = 7 единиц. Точка E делит прямую А А 1 как 5 : 2 . Определить угол между скрещивающимися прямыми В Е и А 1 С .
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат О х у z . Получаем, что начало координат является совпадающим с вершиной A , а О х совпадает с прямой A D , О у с A B , а О z с А А 1 . Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что точка B с координатами ( 0 , 3 , 0 ) , E – ( 0 , 0 , 5 ) , A А – ( 0 , 0 , 7 ) , C – ( 2 , 3 , 0 ) . Исходя из координат, мы можем получить координаты векторов B E → и A 1 C → , необходимые для дальнейшего решения задачи. Получаем, что B E → = ( 0 , – 3 , 5 ) , A 1 C → = ( 2 , 3 , – 7 ) .
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α = a r c cos B E → , A 1 C → B E → · A 1 C → = a r c cos 0 · 2 + ( – 3 ) · 3 + 5 · ( – 7 ) 0 2 + ( – 3 ) 2 + 5 2 · 2 2 + 3 2 + ( – 7 ) 2 = = a r c cos 44 34 · 62 = a r c cos 22 527
Угол между прямыми в пространстве
Пусть в пространстве заданы прямые l и m. Через некоторую точку А пространства проведем прямые l1 || l и m1 || m (рис. 138).
Заметим, что точка А может быть выбрана произвольно, в частности она может лежать на одной из данных прямых. Если прямые l и m пересекаются, то за А можно взять точку пересечения этих прямых (l1 = l и m1 = m).
Углом между непараллельными прямыми l и m называется величина наименьшего из смежных углов, образованных пересекающимися прямыми l1 и m1 ( l1 || l , m1 || m). Угол между параллельными прямыми считается равным нулю.
Угол между прямыми l и m обозначается ( widehat <(l;m)>). Из определения следует, что если он измеряется в градусах, то 0° π /2 .
Найти угол между прямыми АВ и DС1.
Прямые АВ и DС1 скрещивающиеся. Так как прямая DC параллельна прямой АВ, то угол между прямыми АВ и DС1, согласно определению, равен (widehatDC>).
Следовательно, (widehat<(AB;DC_1)>) = 45°.
Прямые l и m называются перпендикулярными, если ( widehat <(l;m)>) = π /2. Например, в кубе
(см. рис. 139) прямая A1D1перпендикулярна прямым DC, DC1, СС1 .
Вычисление угла между прямыми.
Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости. Обозначим через φ величину угла между прямыми l1 и l2, а через ψ – величину угла между направляющими векторами а и b этих прямых.
ψ 90° (рис. 206,6), то φ = 180° – ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин) имеем
Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).
Задача 1. Вычислить угол между прямыми
Направляющие векторы прямых имеют координаты:
По формуле (1) находим
Следовательно, угол между данными прямыми равен 60°.
Задача 2. Вычислить угол между прямыми
За направляющий вектор а первой прямой возьмем векторное произведение нормальных векторов n1 = (3; 0; -12) и n2 = (1; 1; -3) плоскостей, задающих эту прямую. По формуле ( [a; b]=begin i & j & k \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 end ) получаем
$$ a=[n_1; n_2]=begin i & j & k \ 3 & 0 & -12 \ 1 & 1 & -3 end=12i-3i+3k $$
Аналогично находим направляющий вектор второй прямой:
$$ b=begin i & j & k \ 4 & -1 & 1 \ 0 & 1 & 1 end=-2i-4i+4k $$
Но формуле (1) вычисляем косинус искомого угла:
Следовательно, угол между данными прямыми равен 90°.
Задача 3. В треугольной пирамиде МАВС ребра MA, MB и МС взаимно перпендикулярны, (рис. 207);
их длины соответственно равны 4, 3, 6. Точка D – середина [МА]. Найти угол φ между прямыми СА и DB.
Пусть СА и DB – направляющие векторы прямых СА и DB.
Примем точку М за начало координат. По условию зядачи имеем А (4; 0; 0), В(0; 0; 3), С(0; 6; 0), D (2; 0; 0). Поэтому (overrightarrow) = (4; – 6;0), (overrightarrow)= (-2; 0; 3). Воспользуемся формулой (1):
По таблице косинусов находим, что угол между прямыми СА и DB равен приблизительно 72°.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/ugol-mezhdu-skreschivajuschimisja-prjamymi/
http://razdupli.ru/teor/84_ugol-mezhdu-pryamymi-v-prostranstve.php
[/spoiler]
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
-
Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.

- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
![]()
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
![]()
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
![]()
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
![]()
Объем
Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
![]()
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
![]()
Тема 2.
Геометрия в пространстве (стереометрия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
Решаем задачи
Дан куб . Найдите угол между прямыми
и
. Ответ дайте в
градусах.
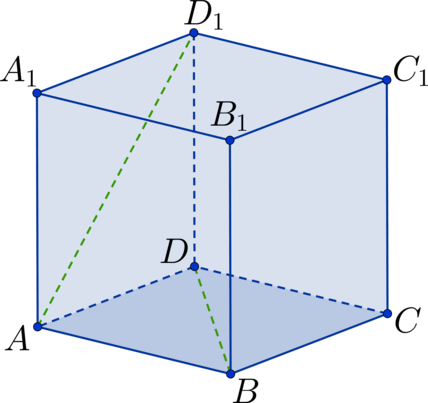
Показать ответ и решение
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота
падает в точку пересечения медиан основания.
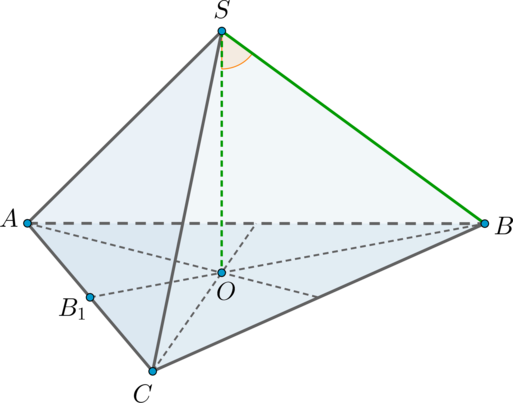
Пусть – медиана, а значит, и высота. По теореме Пифагора
так
как медианы точкой пересечения делятся в отношении , считая от вершины.
Следовательно, прямоугольный является равнобедренным (
), значит, острые
углы равны по .
Показать ответ и решение
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные правильные
треугольники, то есть также является и медианой, значит,
. Также у правильного
тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот)
противоположной грани. Следовательно, если – высота, то
– точка пересечения медиан
треугольника , а значит и высот, так как
правильный. Следовательно,
— медиана
и высота.
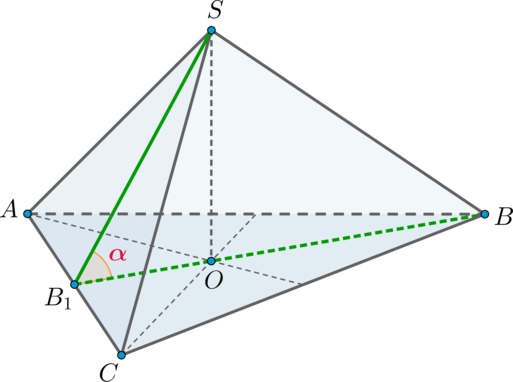
Таким образом, необходимо найти .
Пусть – ребро тетраэдра. Тогда
, следовательно, по теореме Пифагора
Так
как – точка пересечения медиан, а медианы точкой пересечения делятся в отношении
, считая
от вершины, то .
Так как , то
. Следовательно, из прямоугольного
:
Показать ответ и решение
Докажем, что содержит биссектрису угла
. Выберем на
точку
, а на
точку
так, чтобы . Построим прямую, проходящую через точку
и точку
– середину
.
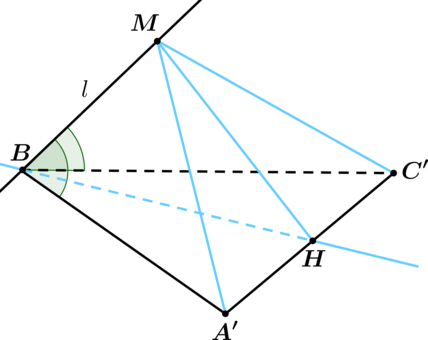
Отметим на точку
. Треугольник
– равнобедренный, тогда
– высота.
Рассмотрим треугольники и
: они равны по двум сторонам и углу между ними, тогда
и треугольник
– равнобедренный, тогда
– его высота.
В итоге и
, следовательно,
. Если предположить, что
–
проекция точки на
, не попадает на прямую, содержащую
, то получим, что
и
, откуда следует, что
. Но тогда плоскости
и
перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не
может.
Таким образом, лежит на прямой, содержащей
, но тогда
совпадает с прямой,
содержащей . В итоге,
.
Показать ответ и решение
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные
правильные треугольники, то есть также является и медианой, значит,
. Также у
правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис,
высот) противоположной грани. Следовательно, если – высота, то
– точка пересечения медиан
треугольника , а значит и высот, так как
правильный. Следовательно,
медиана и
высота.
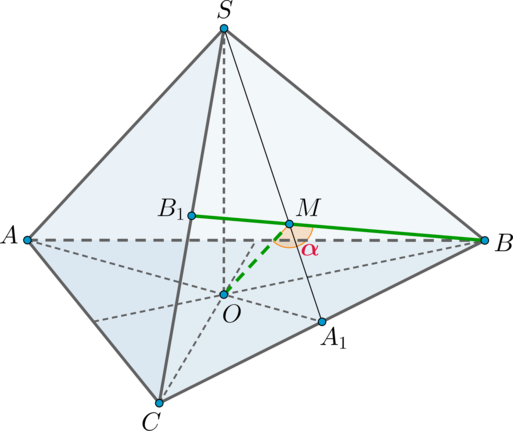
Рассмотрим . Проведем
, следовательно,
.
Заметим также, что будет лежать на
.
Действительно, так как медианы точкой пересечения делятся в отношении , считая от вершины, то
. Следовательно,
(по теореме Фалеса, так как
). Но
и – медианы в
, следовательно, они пересекаются и точкой пересечения тоже делятся в
отношении . А так как
делит
в отношении
, считая от вершины
, то
и есть
точка пересечения медиан и
.
Таким образом, нужно найти .
Пусть – ребро тетраэдра. Тогда
По
теореме Пифагора
Так
как грани тетраэдра равны, то
Следовательно, по теореме косинусов из :
Каталог заданий.
5. Вычисление углов между элементами куба
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 8 № 214 

В кубе найдите угол между прямой
и гранью
Аналоги к заданию № 214: 215 Все
Решение
·
Помощь
2
Тип 8 № 215 

В кубе найдите угол между прямой AB и гранью
Аналоги к заданию № 214: 215 Все
Решение
·
Помощь
3
Тип 8 № 216 

В кубе найдите угол между прямой
и плоскостью
Аналоги к заданию № 216: 217 Все
Решение
·
Помощь
4
Тип 8 № 217 

В кубе найдите угол между прямой
и плоскостью
Аналоги к заданию № 216: 217 Все
Решение
·
Помощь
5
Тип 8 № 218 

В кубе найдите угол между прямой
и плоскостью
Аналоги к заданию № 218: 219 Все
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
![]()
Перед вами очередная статья с параллелепипедами. Представленные задания просты, вычислений никаких нет или их минимум. Рассматриваются кубы и прямоугольные параллелепипеды. Важно грамотно выполнить построения и знать элементарные свойства. Например, в данных заданиях используются:
1. В равностороннем треугольнике все его углы равны 60 градусам.
2. Диагонали граней куба равны.
3. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
4. Необходимо понимание понятия — скрещивающиеся прямые.
Напомню какая призма является правильной.
Правильная призма – это призма основания которой – правильные многоугольники, боковые рёбра расположены под прямым углом к основаниям. Например, правильная треугольная призма – это прямая призма, основания которой равносторонние треугольники.
Правильная четырёхугольная призма – это прямая призма, основания которой являются квадратами. Понятно, что такая призма является прямоугольным параллелепипедом.
Правильная шестиугольная призма – это прямая призма, основания которой являются правильными шестиугольниками. Рассмотрим задачи:

315130. В кубе ABCDA1B1C1D1 точка К — середина ребра АA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Построим куб, обозначим его вершины и точки K, M и L.

Так как данные точки являются серединами ребёр, то отрезки KM, ML, KL будут равны между собой. Это означает, что треугольник KML равносторонний. Известно, что в равностороннем треугольнике его углы равны по 60 градусов. Таким образом, угол MLK равен 600.
Ответ: 60

316554. В кубе ABCDA1B1C1D1 найдите угол между прямыми АD1 и B1D1. Ответ дайте в градусах.
Построим куб, обозначим вершины и данные отрезки, также построим отрезок АВ1.

Отрезки АD1, B1D1 и АD1 являются диагоналями граней куба, то есть все они равны, значит треугольник АD1B1 является равносторонним. Известно, что в равностороннем треугольнике его углы равны по 60 градусов.
Таким образом, угол между прямыми АD1 и B1D1 равен 600.
Ответ: 60

318474. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1.

Построим отрезки CD и A1C1:

В данной задаче имеем скрещивающиеся прямые, то есть сами они не имеют общей точки пересечения. Но этот угол между скрещивающимся прямыми определяется. Как?
Простыми словами: если вы мысленно представите в пространстве две непараллельные прямые, то всегда существует такой перпендикуляр, который их соединяет. Так вот, если мы параллельным переносом сдвинем одну прямую к другой по этому перпендикуляру до пересечения этих прямых, то полученный между ними угол и будет тем самым искомым углом.
В кубах и параллелепипедах, где прямые проходят через рёбра и диагонали такие углы определить несложно. А вот в части С присутствуют задания со скрещивающимися прямыми на порядок сложнее.
Вернёмся к нашей задаче.
Мысленно сдвинем отрезок CD вдоль перпендикуляра СC1 до пересечения с прямой A1C1. Получается, что необходимо найти синус угла между A1C1 и C1D1. Это мы можем сделать воспользовавшись определением синуса в прямоугольном треугольнике А1C1D1. Найдём:
![]()
По определению синуса:

Ответ: 0,6

318475. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что AC1 = 2BC. Найдите острый угол между диагоналями BD1 и CA1. Ответ дайте в градусах.
Построим правильную четырёхугольную призму, обозначим вершины, построим диагонали BD1 и CA1:

Сразу отметим, что диагонали BD1 и CA1 являются диагоналями прямоугольника A1BCD1, то есть они равны между собой и равны диагонали AC1 (так как призма правильная четырехугольная).
Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, то есть:
A1С = D1B
A1O = ОС и D1O = ОB
A1O = ОС = D1O = ОB
В условии сказано, что AC1 = 2BC, значит имеем BD1 = CA1 = 2BC. На основании изложенного можем сделать вывод о том, что:
BO = ОС = BC и A1O = ОD1 = A1D1
то есть треугольники BОС и A1OD1 равносторонние.
Таким образом, угол острый между диагоналями равен 600.
Ответ: 60
![]()
В данных заданиях используется теорема Пифагора, для нахождения углов необходимо владеть понятиями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике.
245359. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.

Посмотреть решение
245360. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.

Посмотреть решение
245361. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.

Посмотреть решение
245362. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.

Посмотреть решение
245363. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.

Посмотреть решение
284357. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 3, CD = 2, AD = 2. Найдите длину ребра AA1.

Посмотреть решение
284363. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.

Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
