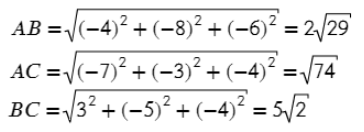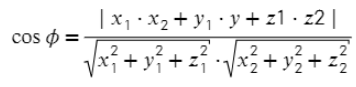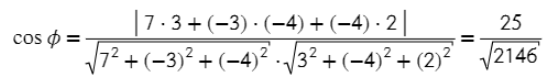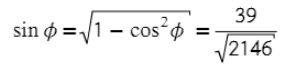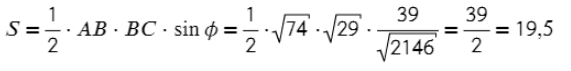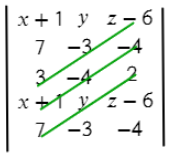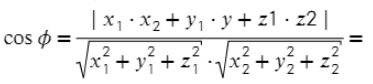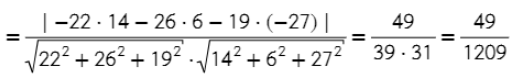Угол между векторами
Определение
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
(left(widehat{overrightarrow a;overrightarrow b}right))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
Острый:
Тупой:
Прямой:
С величиной (0^circ) (то есть, векторы сонаправлены):
С величиной (180^circ) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Определение
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.
В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Расчет угла, если вектор задан координатами
В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Если же координаты находятся в трехмерном пространстве и заданы в виде:
(overrightarrow a=left(a_x;a_y;a_zright))
( overrightarrow b=left(b_x;b_y;b_zright))
то формула принимает такой вид:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).
Решение
Для начала найдем их координаты по известным координатам заданных точек:
(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))
(overrightarrow{BC}=(6-2, -1-1)=(4,-2))
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})
Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.
Решение
Применим формулу:
( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Подставим известные значения:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)
Далее найдем угол между данными векторами:
(arccosleft(-frac12right)=frac{3pi}4)
Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)
Задача 2
В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Подставляем значения и получаем:
(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})
Теперь находим угол α:
(alpha=arccosleft(frac2{sqrt2}right)=45^circ)
Ответ: (45^circ).
Задача 3
Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.
Решение
Для расчета используем формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Подставим известные значения и получим:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})
Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})
eigenbasis
Гуру
(3250)
1 год назад
1. находим вектора, образующие угол (BA и BC):
BA = A – B = (-1, 1)
BC = C – B = (-1, -1)
2. находим скалярное произведение этих векторов
⟨BA, BC⟩ = (-1)*(-1) + 1*(-1) = 0
3. находим длины этих векторов (конкретно здесь уже ясно, что угол 90 градусов, но для других координат точек этот шаг надо было бы сделать)
|BA| = √((-1)² + (1)²) = √2
|BC| = √((-1)² + (-1)²) = √2
4. косинус угла между векторами равен их скалярному произведению, делённому на произведение длин этих векторов, то есть
cos(ABC) = ⟨BA, BC⟩ / (|BA| * |BC|) = 0 / 2 = 0
Поэтому угол ABC = 90 градусов
Альтернативный способ (если вы знаете, что такое определитель матрицы 2х2).
1. опять находим координаты образующих векторов
BA = (-1, 1) и BC = (-1, -1)
2. составляем из них матрицу и находим её определитель
| -1 -1 |
| 1 -1 | = (-1)*(-1) – (-1)*1 = 2
из геометрического смысла определителя он равен удвоенной площади треугольника, то есть 2*S(ABC) = 2
3. делим определитель на произведение длин векторов и из формулы площади треугольника через синус получаем синус нашего угла
sin(ABC) = 2 / (√2 * √2) = 2 / 2 = 1
отсюда аналогично заключаем, что угол 90 градусов
eigenbasisГуру (3250)
1 год назад
Из ответа ниже правда стоило бы считать не определитель, а его модуль (ориентация площади нам правда здесь не очень инетесна)
Тадасана
Просветленный
(32166)
1 год назад
Применяем оба способа 1 и 2
Площадь параллелограмма-то ориентированная, это ж симплектическое скалярное пргизведение, согласованное с евклидовым скалярыным произведением в E2, оно называется псевдокакое-то.
Зная синус и косинус угла, найдем и угол с т. до 2пи, если считать, что он гткладывается против часовй
Имеем три точки с координатами – A, B и C, точки образуют отрезки AB и AC, необходимо определить угол α между этими отрезками:
1
PHP-функция
$x1, $y1 – координаты точки A,
$x2, $y2 – координаты точки B,
$x3, $y3 – координаты точки C.
function getAnglePoints($x1, $y1, $x2, $y2, $x3, $y3)
{
return rad2deg(atan2($y3 - $y1, $x3 - $x1) - atan2($y2 - $y1, $x2 - $x1));
}PHP
2
JS-функция
function getAnglePoints(x1, y1, x2, y2, x3, y3)
{
return (Math.atan2(y3 - y1, x3 - x1) - Math.atan2(y2 - y1, x2 - x1)) * 180 / Math.PI;
}JS
3
Угол между тремя точками по координатам онлайн
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a→ и b→ , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы OA→=b→ и OB→=b→
Углом между векторами a→ и b→ называется угол между лучами ОА и ОВ.
Полученный угол будем обозначать следующим образом: a→,b→^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a→,b→^=0, когда векторы являются сонаправленными и a→,b→^=π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π2 радиан.
Если хотя бы один из векторов является нулевым, то угол a→,b→^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a→, b→=a→·b→·cosa→,b→^.
Если заданные векторы a→ и b→ ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cosa→,b→^=a→,b→a→·b→
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a→ и b→ . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно -9. Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cosa→,b→^=-93·6=-12 ,
Теперь определим угол между векторами: a→,b→^=arccos (-12)=3π4
Ответ: cosa→,b→^=-12, a→,b→^=3π4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a→=(ax, ay), b→=(bx, by) выглядит так:
cosa→,b→^=ax·bx+ay·byax2+ay2·bx2+by2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a→=(ax, ay, az), b→=(bx, by, bz) будет иметь вид: cosa→,b→^=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
Исходные данные: векторы a→=(2, 0, -1), b→=(1, 2, 3) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cosa→,b→^=2·1+0·2+(-1)·322+02+(-1)2·12+22+32=-170⇒a→,b→^=arccos(-170)=-arccos170
- Также можно определить угол по формуле:
cosa→,b→^=(a→, b→)a→·b→,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a→=22+02+(-1)2=5b→=12+22+32=14a→,b→^=2·1+0·2+(-1)·3=-1cosa→,b→^=a→,b→^a→·b→=-15·14=-170⇒a→,b→^=-arccos170
Ответ: a→,b→^=-arccos170
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A(2, -1), B(3, 2), C(7, -2). Необходимо определить косинус угла между векторами AC→ и BC→.
Решение
Найдем координаты векторов по координатам заданных точек AC→=(7-2, -2-(-1))=(5, -1)BC→=(7-3, -2-2)=(4, -4)
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cosAC→, BC→^=(AC→, BC→)AC→·BC→=5·4+(-1)·(-4)52+(-1)2·42+(-4)2=2426·32=313
Ответ: cosAC→, BC→^=313
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы OA→=a→ и OB→=b→ , тогда, согласно теореме косинусов в треугольнике ОАВ, будет верным равенство:
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) ,
что равносильно:
b→-a→2=a→+b→-2·a→·b→·cos(a→, b→)^
и отсюда выведем формулу косинуса угла:
cos(a→, b→)^=12·a→2+b→2-b→-a→2a→·b→
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
cos(a→, b→)^=a→, b→a→·b→
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Метод координат (углы между векторами и плоскостями)
Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.
Решение задач с доказательством.
Для того, чтобы успешно решать задачи методом координат, полезно помнить:
Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.
Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.
Задача. Найти координаты и длины векторов AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).
AB = (1−5; 0-8; −3−3) = (−4; −8; −6)
AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)
BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)
Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):
Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Вычисляем косинус угла между векторами.
- Через основное тригометрическое тождество получаем синус.
- Подставляем в формулу площади.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Задаем матрицу плоскости.
- Вычисляем ее определитель, это и есть уравнение плоскости.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
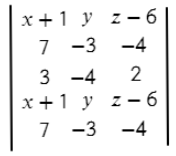
Вторая строчка – координаты первого вектора.
Третья строчка – координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).
Четвертая заполняется аналогично первой.
Пятая – аналогично второй.
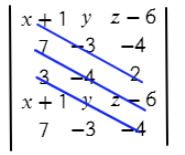
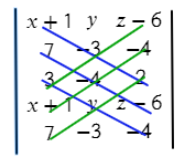
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)
Аналогично делаем с зелеными отрезками:
(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7
Осталось из значений синих отрезков вычесть значения зеленых отрезков:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =
= −22х −26y −19z + 92
−22х −26y −19z + 92 – искомое уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета – это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.
Задача. Найдите угол между плоскостью, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением
14x + 6y −27z + 51 = 0.
- Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
- Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).
Будь в курсе новых статеек, видео и легкого математического юмора.