Как найти угол между вектором и плоскостью
Вектор – направленный отрезок прямой, имеющий определенную длину. В пространстве он задается тремя проекциями на соответствующие оси. Можно найти угол между вектором и плоскостью, если она представлена координатами своей нормали, т.е. общим уравнением.

Инструкция
Плоскость – это основная пространственная фигура геометрии, которая участвует в построении всех двухмерных и трехмерных форм, таких как треугольник, квадрат, параллелепипед, призма, окружность, эллипс и т.д. В каждом конкретном случае она ограничивается определенным набором линий, которые, пересекаясь, образуют замкнутую фигуру.
В общем же виде плоскость не ограничивается ничем, она простирается по разные стороны от своей образующей прямой. Это плоская бесконечная фигура, которая, тем не менее, может быть задана уравнением, т.е. конечными числами, которые являются координатами ее нормального вектора.
Исходя из вышесказанного, можно найти угол между любым вектором и плоскостью, используя формулу косинуса угла между двумя векторами. Направленные отрезки могут быть расположены в пространстве как угодно, однако каждый вектор обладает таким свойством, что его можно перемещать без потери основных характеристик, направления и длины. Этим и нужно воспользоваться, чтобы рассчитать угол между отстоящими векторами, поместив их зрительно в одну начальную точку.
Итак, пусть задан вектор V = (а, b, с) и плоскость А•x + В•y + C•z = 0, где А, В и C – координаты нормали N. Тогда косинус угла α между векторами V и N равен:сos α = (а•А + b•В + с•C)/(√(а² + b² + с²)•√(А² + В² + C²)).
Чтобы вычислить величину угла в градусах или радианах, нужно от получившегося выражения рассчитать функцию, обратную к косинусу, т.е. арккосинус:α = аrссos ((а•А + b•В + с•C)/(√(а² + b² + с²)•√(А² + В² + C²))).
Пример: найдите угол между вектором (5, -3, 8) и плоскостью, заданной общим уравнением 2•x – 5•y + 3•z = 0.Решение: выпишите координаты нормального вектора плоскости N = (2, -5, 3). Подставьте все известные значения в приведенную формулу:сos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Пусть
задан вектор
 ,
,
перпендикулярный к плоскости (вектор нормали) и точка
(вектор нормали) и точка – произвольная фиксированная точка
– произвольная фиксированная точка
плоскости. Возьмем на плоскости произвольную
произвольную
нефиксированную точку –
–
(текущая точка) (рис.8).

Рис.8
Вектор
 ,
,
лежащий в плоскости ,
,
перпендикулярен вектору нормали ,
,
значит их скалярное произведение ,
,
следовательно

Полученное
уравнение – уравнение
плоскости, проходящей через точку
 ,перпендикулярно
,перпендикулярно
вектору
 .
.
Пример.
Составить уравнение плоскости, проходящей
через точку и перпендикулярно вектору
и перпендикулярно вектору ,
,
если ,
, (рис.9).
(рис.9).
Решение.
Пусть
 – текущая точка искомой плоскости
– текущая точка искомой плоскости .
.
Найдем координаты векторов

 .
.
Вектор
 принадлежит плоскости
принадлежит плоскости и перпендикулярен вектору
и перпендикулярен вектору ,
,
значит их скалярное произведение



–
уравнение плоскости
 .
.
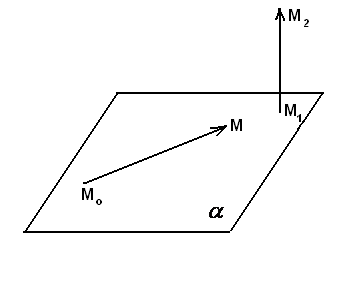
Рис.9
Рассмотрим
плоскость, проходящую через три точки,
не лежащие на
одной прямой:
 – (рис.10).
– (рис.10).
Точка –
–
текущая точка плоскости.

Рис.10
Три
вектора:
 ,
,

лежат
в одной плоскости, значит компланарны,
и их смешанное произведение равно нулю:

Запишем
смешанное произведение в координатной
форме, получим:
 –
–
уравнение
плоскости, проходящей
через
три точки.
Пример.
Найти уравнение плоскости, проходящей
через три точки
 (рис.11).
(рис.11).

Рис.11
Решение.
Пусть точка
 – текущая точка плоскости. Найдем
– текущая точка плоскости. Найдем
координаты трех компланарных векторов: ,
, ,
, .
.
Смешанное
произведение векторов равно нулю:




 –
–
уравнение плоскости
 .
.
Пусть
плоскость
 задана общим уравнением
задана общим уравнением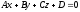 .
.
Расстояние
от точки
 до плоскости
до плоскости
 (рис12)
(рис12)
вычисляют по формуле
 .
.

Рис.12
Пример.
Найти расстояние от точки
 до плоскости
до плоскости .
.
Решение.
Воспользуемся
формулой расстояния от точки до плоскости,
получим:
 .
.
Угол
между плоскостями
равен углу
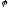
между их
векторами нормалей (рис.13).
Пусть
даны две плоскости:
плоскость с нормалью
с нормалью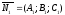
плоскость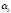
с нормалью


Рис.13
Косинус
угла между плоскостями вычисляется по
формуле:
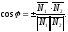
Пример.
Найти угол между плоскостями
 ;
;
 .
.
Решение.
Векторы нормалей имеют координаты:


 Отсюда,
Отсюда,

Уравнения
прямой в пространстве
Рассмотрим
в пространстве прямую a,
проходящую через точку
 параллельно
параллельно
вектору ,
,
который называется направляющим вектором
прямойа
(рис.14).

Рис.14
Пусть
точка
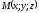 – текущая точка прямой. Вектор
– текущая точка прямой. Вектор лежит на прямой и коллинеарен вектору
лежит на прямой и коллинеарен вектору .
.
Из условия коллинеарности двух векторов,
имеем:
Эти
уравнения – канонические
уравнения прямой в пространстве.
Если
в канонических уравнениях ввести
параметр t:
 ,
,
получимпараметрические
уравнения прямой:

Прямую
можно задать как линию пересечения двух
плоскостей (рис.15):

Рис.15
 –
–
общие
уравнения прямой в пространстве.
Уравнения
прямой, проходящей через две точки
 и
и :
:
Угол
между прямыми
равен острому углу между их направляющими
векторами (рис.16) и вычисляется по
формуле:


Рис.16
Пример.
Прямая
 задана общими уравнениями
задана общими уравнениями

а)
Написать для этой прямой канонические
и параметрические уравнения;
б)
Найти угол между прямой
 и прямой
и прямой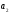 ,заданной
,заданной
уравнениями

Решение.
а)
Выберем
одну из точек, через которую пройдет
указанная прямая, заданная пересечением
плоскостей. Исходная система имеет
бесчисленное множество решений, одно
из которых получим придавая одной из
переменных конкретное значение. Пусть
 ,
,
тогда значения других неизвестных
находим из системы
Решением
этой системы является пара чисел
 .
.
В
результате получим точку
 ,
,
через которую проходит искомая прямая.
В качестве направляющего вектора прямой
можно взять вектор ,
,
где ,
,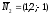 –
–
нормальные векторы плоскостей, линией
пересечения которых является прямая.
Таким образом,
 .
.
Запишем
канонические уравнения прямой
 :
:
Получим
из канонических параметрические
уравнения прямой:

б)
Направляющий вектор прямой
 ,
,
направляющий вектор прямой
 Угол
Угол
между прямыми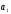 и
и равен острому углу между их направляющими
равен острому углу между их направляющими
векторами:


Угол
между прямой и плоскостью
Пусть
заданы прямая a
и плоскость
 (рис.17):
(рис.17):
Прямая

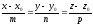 c
c
направляющим вектором

Плоскость

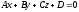 с вектором нормали
с вектором нормали

Рис.17
Угол

между прямой
а
и плоскостью
 вычисляется
вычисляется
по формуле:
Чтобы
найти точку
пересечения прямой и плоскости,
нужно параметрические уравнения прямой
 подставить
подставить
в уравнение плоскости и
и
найти параметр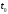 ,
,
соответствующий точке пересечения.
Пример.
Найти а)
угол между прямой и плоскостью;
б)
точку пересечения прямой и плоскости.
 .
.
Решение.
 –
–
нормаль к плоскости;
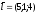 –
–
направляющий вектор прямой.
а)

Отсюда,

б)
Подставим параметрические уравнения
прямой
 в уравнение плоскости
в уравнение плоскости
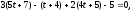
 ,
,
 –
–
параметр точки пересечения прямой и
плоскости.
Подставим
значение параметра

в
параметрические уравнения, получим:
 Координаты точки пересечения
Координаты точки пересечения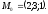
Уравнение
прямой на плоскости
Каноническое
уравнение прямой на плоскости:
 ,
,
где –
–
направляющий вектор прямой.
Общее
уравнение прямой на плоскости:
 ,
,
где
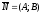
– вектор
нормали прямой.
Уравнение
прямой с угловым коэффициентом
 (рис.18),
(рис.18),
где – угловой коэффициент прямой; угол
– угловой коэффициент прямой; угол –
–
угол между прямой и осьюОХ;
b
– отрезок, отсекаемый прямой на оси OY.

Рис.18
Уравнение
прямой, проходящей через две точки
 и
и :
: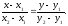
Пример
Даны точки
А(2;5),
В(-3;1),
С(5;2).
Найти: а)
а)
уравнение медианыAD;
б)
уравнение высоты AE;
в)
угол между медианой AD
и высотой AE;
г)
уравнение прямой, проходящей через
точку С,
параллельно прямой АВ
(рис19).

Рис.19
Решение.
а)
Точка D
– середина
отрезка ВС,
найдем ее координаты:
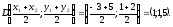
Прямая
AD
проходит через две точки. Её уравнение
имеет вид:
 ;
;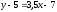 ;
;
 –
–
уравнение прямой AD.
б)
Высота
перпендикулярна ВС.
Пусть точка Е
имеет координаты
 Тогда
Тогда
векторы
следовательно,
их скалярное произведение

 – уравнение высотыАЕ.
– уравнение высотыАЕ.
в)
Угол
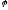
между
медианой AD
и высотой АЕ
– это угол между их векторами нормалей
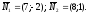

Отсюда,
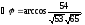
г)
Прямая СК
параллельна прямой АВ.
Пусть точка K
имеет координаты
 Тогда
Тогда
векторы
и
 коллинеарны.
коллинеарны.
Отсюда,
 ;
; ;
;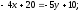
 –
–
уравнение прямой СК,
параллельной АВ.
Соседние файлы в папке 1 семестр
- #
- #
- #
27.03.20162.06 Mб19Metodich_posobie_Khimia.doc
- #
- #
Иногда студенты при решении задач аналитической геометрии сталкиваются с вопросом: «Как найти угол между векторами?». Чтобы решить такую задачу нужно сначала найти косинус угла между ними, а затем и сам угол. Для этого применяется такая формула: $$ phi = arccos(cos phi) $$
Если воспользоваться данной формулой, то сначала нужно найти угол между векторами $ cos phi $. Затем находим арккосинус от косинуса угла $ phi $. А чему равен $ cos phi $? Для его нахождения необходимо воспользоваться следующими формулами.
Формула
Если векторы расположены на плоскости и координаты их заданы в виде: $ overline = (a_x; a_y) $ и $ overline = (b_x; b_y) $, то найти угол между ними можно так:
Если вектора находятся в пространстве и координаты каждого из них заданы в виде: $ overline = (a_x; a_y; a_z) $ и $ overline = (b_x; b_y; b_z) $, то вычислить косинус угла следует по формуле:
Примеры решений
Сначала находим косинус угла между векторами по формуле:
Теперь искомый угол $ phi $ находим по другой формуле:
$$ phi = arccos (cos phi) = arccos (cos frac<sqrt<2>><2>) = 45^0 $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример 1 |
| Найти угол между векторами $ overline = (2;4) $ и $ overline = (3;1) $ |
| Решение |
| Ответ |
| Угол между двумя векторами равен $ phi = 45^0 $ |
Подставляем координаты в формулу и вычисляем:
Далее находим сам угол $ phi $ с помощью арккосинуса:
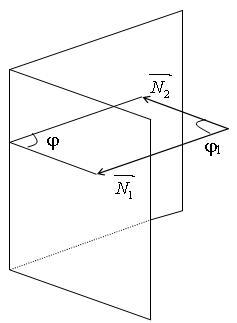
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: 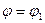 или
или 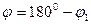 , т.е.
, т.е. 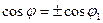 .
.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:
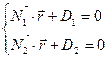 ,
,
где 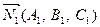 ,
, 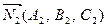 .
.
Угол между векторами нормали найдем из их скалярного произведения:
 .
.
Таким образом, угол между плоскостями находится по формуле:
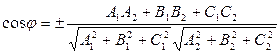
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Условия параллельности и перпендикулярности плоскостей
На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.
Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
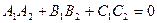 .
.
Плоскости параллельны, векторы нормалей коллинеарны: 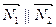 . Это условие выполняется, если:
. Это условие выполняется, если:  .
.
| Пример 2 |
| Найти угол $ phi $ между двумя векторами $ overline = (8;-11;7) $ и $ overline = (-2;-7;8) $ |
| Решение |
| | | следующая лекция ==> | |
| Общие уравнения прямой в пространстве | | | Угол между прямыми в пространстве |
Дата добавления: 2014-01-05 ; Просмотров: 500 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
29
Мар 2012
13 Задание (2022) (C2)
 В этой статье я еще раз покажу вам решение задачи на нахождение угла между плоскостями с помощью метода координат. Мы воспользуемся тем фактом, что угол между плоскостями равен углу между прямыми, содержащими нормали к этим плоскостям.
В этой статье я еще раз покажу вам решение задачи на нахождение угла между плоскостями с помощью метода координат. Мы воспользуемся тем фактом, что угол между плоскостями равен углу между прямыми, содержащими нормали к этим плоскостям.
Задача такая:
Основание прямой четырехугольной призмы  – прямоугольник
– прямоугольник  , в котором
, в котором  ,
,  . Найдите косинус угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра
. Найдите косинус угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра  перпендикулярно прямой
перпендикулярно прямой  , если расстояние между прямыми
, если расстояние между прямыми  и
и 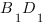 равно 5.
равно 5.
Геометрическое решение этой задачи весьма неочевидно, однако, с помощью метода координат она решается в одно действие.

Заметим несколько важных вещей:
1. Угол между плоскостью основания и плоскостью, перпендикулярной прямой  , не зависит от точки, через которую проведена эта плоскость. Поэтому мы эту точку даже не будем наносить на чертеж.
, не зависит от точки, через которую проведена эта плоскость. Поэтому мы эту точку даже не будем наносить на чертеж.
2. Прямые  и
и 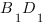 лежат в параллельных плоскостях
лежат в параллельных плоскостях  и
и  , поэтому расстояние между ними равно расстоянию между плоскостями, то есть высоте призмы. Отсюда
, поэтому расстояние между ними равно расстоянию между плоскостями, то есть высоте призмы. Отсюда  .
.
3. Боковые ребра прямой призмы перпендикулярны плоскости основания.
Поместим нашу призму в систему координат и нанесем на чертеж данные задачи:
 Вспомним, что
Вспомним, что
1. В уравнении плоскости  коэффициенты
коэффициенты  являются координатами вектора нормали к плоскости.
являются координатами вектора нормали к плоскости.
2. Угол между плоскостями равен углу между прямыми, содержащими нормали к этим плоскостям (как углы со взаимно перпендикулярными сторонами)
Получается, что в этой задаче нам нужно найти угол между вектором  ( по условию задачи плоскость проведена перпендикулярно прямой
( по условию задачи плоскость проведена перпендикулярно прямой  ) и вектором
) и вектором  (это вектор нормали к плоскости основания).
(это вектор нормали к плоскости основания).
Косинус угла 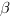 между векторами
между векторами 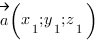 и
и 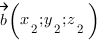 вычисляется по формуле:
вычисляется по формуле:
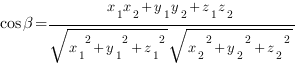
Найдем координаты вектора 




Пусть 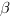 – угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра
– угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра  перпендикулярно прямой
перпендикулярно прямой  .
.
Тогда 
Ответ: 
И.В. Фельдман, репетитор по математике.

|
Отзывов (11)
| Метки: решение задания С2
«Использование метода координат в пространстве для решения задачи №13 Единого государственного экзамена»
Как всем известно, для учеников старших классов самой насущной проблемой является Единый государственный экзамен. Причём, тех учеников, которые с уверенностью могут сказать: «Я могу решить 13 или 16 задачу», всего единицы. Да и те, кто действительно могут решить их, об этом громко не заявляют.
Анализируя данную проблему, можно сказать, что большая часть выпускников ограничивается заданием 13 пункта а). А при решении пункта б) уже возникают проблемы.
Как вы знаете, в задании 13 чаще всего требуется найти:
1) угол между двумя скрещивающимися прямыми, между прямой и плоскостью, между двумя плоскостями;
2) расстояние между двумя скрещивающимися прямыми, расстояние от точки до прямой, от точки до плоскости.
В своей работе я предлагаю использовать один из универсальных приёмов решения геометрических задач – метод координат в пространстве. Мы уже хорошо знакомы с векторами, координатами и их свойствами. Цель моей работы: научиться применять знания для решения задач стереометрии.
Однако формальное применение координатно-векторного метода может значительно затруднить решение даже самой простой задачи. Поэтому я привожу несколько общих указаний, которые помогут сориентироваться и решить, можно ли в данной задаче использовать векторы и координаты.
Во-первых, естественно, нужно применять координатный или векторный метод, если в условиях задачи говорится о векторах или координатах;
Во-вторых, очень полезно применить координатный метод, если из условия задачи не понятно, как расположены те или иные точки;
В-третьих, что для нас особенно важно, полезно и удобно применять координаты и векторы для вычисления углов и расстояний;
В-четвертых, вообще, часто, когда не видно ни каких подходов к решению задачи, можно попробовать применить координатный метод. Он не обязательно даст решение, но поможет разобраться с условиями и даст толчок к поиску другого решения.
2.1. Кратко из теории4
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Существует множество систем координат: аффинная, полярная, биполярная, коническая, параболическая, проективная, сферическая, цилиндрическая и др. Наиболее используемая из них — прямоугольная система координат (также известная как декартова система координат). Ею мы и будем пользоваться для решения задач.
Прямоугольная (декартова) система координат – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy и Oz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.
Применение метода координат даёт нам множество возможностей для решения задач.
- Нахождение расстояния между двумя точками, заданными своими координатами.

где d=AB, A(x1; y1; z1), B(x2; y2; z2)
2. Нахождение координаты середины С(x; y; z) отрезка АВ, A(x1; y1; z1), B(x2; y2; z2).  ,
,  ,
, 
 3. Нахождение косинуса, а, следовательно, и самого угла, между двумя векторами, заданными своими координатами.
3. Нахождение косинуса, а, следовательно, и самого угла, между двумя векторами, заданными своими координатами.
где .
4. Нахождение угла между плоскостями путем составления уравнения каждой плоскости Ах+Ву+Сz+D=0 и определения угла между нормалями к плоскостям. Нормаль n при этом имеет координаты .
5.Нахождение расстояния от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно.

6. Координаты x, y, z точки М, которая делит отрезок  , ограниченный точками
, ограниченный точками  (
( ,
,  ,
,  ) и
) и  (
( ,
,  ,
,  ), в отношении
), в отношении  , определяется по формулам
, определяется по формулам
 ,
,  ,
,  .
.
2.2. Нахождение угла между скрещивающимися прямыми
- Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
- 0˚<(a,α)<90˚.
При нахождении угла между прямыми используют:
формулу или в координатной форме
для нахождения угла φ между прямыми m и l, если векторы и параллельны соотвественно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы или .
Пример 1.5 Сторона основания правильной четырехугольной призмы ABCDA1B1C1 D1 равна 2, высота — 4. Точка E — середина отрезка CD, точка F — середина отрезка AD. Найдите угол между прямыми CF и B1E.
х
у
z
B1
A1
C1
D1
B C
A E
F D
Решение.
Для начала сделаем чертёж и проанализируем задачу.
Прямые CF и B1E являются скрещивающимися, поэтому, чтобы найти угол между ними геометрическим способом, было бы необходимо параллельно перенести одну из прямых так, чтобы обе прямые лежали на одной плоскости. При этом было бы довольно сложно определить, в каком соотношении они будут пересекаться, и решить эту задачу поэтапно-вычислительным методом.
Я предлагаю поместить параллелепипед в прямоугольную систему координат, как показано на рисунке, и найти искомый угол как угол между векторами.
Выпишем координаты точек B1, E, C, F в этой системе координат:
B1 (0; 0; 4), E(1; 2; 0), C(0; 2; 0), F (2; 1; 0).
Тогда {2; -1; 0}, {1; 2; -4}. Найдём угол между этими векторами по формуле:

То есть искомый угол α=90˚.
Как видите, задачу, которую довольно-таки сложно решить геометрическим путём, можно быстро и красиво решить аналитически.
Ответ: 90˚.
Пример 2.2 Точка О лежит на ребре DD1 куба ABCDA1B1C1 D1, точка Р является точкой пересечения диагоналей грани ABCD. DO : DD1 = 1 : 5. Найдите косинус угла между прямой ОР и прямой, содержащей диагональ куба, выходящую из вершины С.
 Решение.
Решение.
Поместим куб в прямоугольную систему координат, как показано на рисунке. Условно обозначим грани куба за единицу. Если обозначить её какой-либо буквой, она всё равно сократится. Определим координаты точек Р, О, С и А1:
О
Р
Р(0,5; 0,5; 0), О(1; 1; 0,5), С(0; 1; 0), А1(1; 0; 1).
Отсюда .
Ответ: .
Пример 3.5 Основанием пирамиды SABC является равносторонний треугольник ABC, сторона которого равна . Боковое ребро SC перпендикулярно плоскости основания и равно 1. Найдите угол между скрещивающимися прямыми, одна из которых проходит через точку S и и середину ребра DC, а другая проходит через точку C и середину ребра AB.
 Решение.
Решение.
Поместим пирамиду в декартову систему координат. Найдём координаты точек S, L, C и M: S(0;0;1), L(0;;0), C(0;0;0). Чтобы найти координаты точки М, воспользуемся геометрией: в равностороннем треугольнике все углы равны 60˚, а т.М, которая делит сторону АВ пополам, является не только медианой, но и биссектрисой, поэтому .
Для равностороннего треугольника , х(СМ)=СМ·соs60˚=, у(СМ)=СМ·соs30˚=, {}, SL{0;;-1}
Решая аналогично предыдущим примерам, находим, что .
Ответ: 45˚.
2.3. Нахождение угла между прямой и плоскостью
- Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и её проекцией на данную плоскость.
- 0˚<(a,α)<90˚.
Угол между прямой l и плоскостью α можно вычислить:
по формуле или в координатах , где
– вектор нормали к плоскости α,
– направляющий векор прямой l;
 Пример 4.5 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.
Пример 4.5 В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра АВ и АА1 равны 1, а ребро АD=2. Точка Е – середина ребра В1С1. Найдите угол между прямой ВЕ и плоскостью АВ1С.
Решение. Для решения этой задачи необходимо воспользоваться уравнением плоскости, имеющим общий вид
ах+bу+cz+d=0, где a, b и c – координаты нормали к плоскости.
Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В1(0;0;1), С(0;2;0).
Решая систему
находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а= -d, b=,
c=-d. Таким образом, уравнение примет вид или, после упрощения, 2х+у+2z-2=0. Значит нормаль n к этой плоскости имеет координаты .
Длину вектора легко найти геометрически: . Но его координаты нам всё равно необходимы. Из простых вычислений находим, что .
Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:
.
Ответ: 45˚
2.4. Нахождение угла между двумя плоскостями
- Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
- Величина двугранного угла принадлежит промежутку(0˚; 180˚)
- Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚; 90˚].
- Угол между двумя параллельными плоскостями считается равным 0˚.
Угол между двумя пересекающимися плоскостями можно вычислить:
как угол между нормалями по формуле или в координатной форме , где – вектор нормали плоскости А1х+В1у+С1z+D1=0, – вектор нормали плоскости A2x+B2y+C2z+D2=0.
 Пример 5.1 В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1 Е и D1FC, где точки Е и F-середины ребер А1В1 и В1С1 соответственно.
Пример 5.1 В единичном кубе АВСDA1В1С1D1 найдите угол между плоскостями АD1 Е и D1FC, где точки Е и F-середины ребер А1В1 и В1С1 соответственно.
Решение.
Введём прямоугольную систему координат. Тогда А(0;0;0), С(1;1;0), D1(1;0;1), E(0;0,5;1), F(0,5;1;1).
1) Решая систему
, составляем уравнение плоскости (АD1E): x+2y-z=0.
2) плоскость CFD1:
отсюда находим уравнение 2x+y+z-3=0. Найдём искомый угол как угол между нормалями плоскостей.
, , откуда φ=60˚ Ответ: 60˚
2.5. Нахождение расстояния между двумя точками.
Расстояние между точками А и В можно вычислить:
по формуле ,
где A(x1; y1; z1), B(x2; y2; z2);
по формуле .
Пример 6.6 В основании пирамиды SABCD лежит ромб со стороной 2 и острым углом в 60˚. Боковое ребро SA перпендикулярно основанию пирамиды и равно 4. Найдите расстояние от середины Н ребра SD и серединой М ребра ВС.
 Решение. Поместим пирамиду в прямоугольную систему координат, как показано на рисунке.
Решение. Поместим пирамиду в прямоугольную систему координат, как показано на рисунке.
Найдём координаты точки Н как координаты середины отрезка SD: S(0; 0; 4), D(0; 2; 0).
Чтобы найти координаты точек В и С, найдём координаты их проекций на оси. АВх=ACx=2·cos30˚=, ABy=ACу–2=2·cos60˚=1.
Отсюда В(; 1; 0), С(; 3;0). Тогда координаты точки М равняются:
.
Теперь находим расстояние между точками, заданными своими координатами:
Ответ: .
Пример 7.1 В единичном кубе АВСDA1В1С1D1 точки Е и К – середины ребер АА1 и СD соответственно, а точка М расположена на диагонали В1D1 так, что В1М = 2МD1. Найдите расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK

Решение. Введём декартову систему координат. E(1;0;0,5), K(0,5;1,0), В1(0;0;1), D1(1;1;1). Чтобы вычислить координаты т.М, воспользуемся формулой для нахождения координат точки, которая делит отрезок B1D1 в отношении λ=2:1:
 ,
,  ,
,  .
.
Аналогично находим координаты точки L:
.
Координаты точки Q находим по формуле координат середины отрезка:
 ,
,  ,
,  .
.
Ответ: .
2.6. Нахождение расстояния от точки до плоскости.
Расстояние от точки до плоскости , не содержащей эту точку , есть длина отрезка перпендикуляра , опущенного из этой точки на плоскость .
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
Расстояние от точки М до плоскости α
вычисляется по формуле , где М(х0;у0;z0), плоскость α задана уравнением ax+by+cz+d=0;
Пример 8.2 В кубе АВСDA1B1C1D1 проведена диагональ B1D. В каком отношении, считая от вершины B1, плоскость А1BC1 делит диагональ B1D?

Решение. Составим уравнение плоскости А1BC1 и найдём расстояние от этой плоскости до каждой из точек B1 и D. Пусть l – ребро куба.
В(0;0;0), А1(l;0;l), С1(0;l;l).
Решив систему определяем, что уравнение плоскости имеет вид: x+y–z=0 → а=1, b=1, c= –1. B1(0;0;1), D(1;1;0).
Теперь найдём расстояние от каждой точки до плоскости по формуле
:
Ответ: 2:1.
Пример 9.5 Основание прямой призмы АВСА1В1С1 – равнобедренный треугольник АВС, основание АС и высота ВD которого равны 4. Боковое ребро равно 2. Через середину К отрезка В1С проведена плоскость, перпендикулярная к этому отрезку. Найдите расстояние от вершины А до этой плоскости.
 Решение. Выберем систему координат как показано на рисунке и выпишем координаты вершин данной призмы и точки К в этой системе координат: А(0;–2;0), В(0;0;0), С(0;2;0), В1(4;0;2), К(2;1;1). Тогда . Этот вектор перпендикулярен плоскости, значит, он является его нормалью. К тому же плоскость проходит через точку К. То есть уравнение плоскости имеет вид –2(x–2)+2(у–1)–2(z–1)=0 или, после упрощения, 2x–y+z-4=0.
Решение. Выберем систему координат как показано на рисунке и выпишем координаты вершин данной призмы и точки К в этой системе координат: А(0;–2;0), В(0;0;0), С(0;2;0), В1(4;0;2), К(2;1;1). Тогда . Этот вектор перпендикулярен плоскости, значит, он является его нормалью. К тому же плоскость проходит через точку К. То есть уравнение плоскости имеет вид –2(x–2)+2(у–1)–2(z–1)=0 или, после упрощения, 2x–y+z-4=0.
Теперь находим расстояние от т.А(0;-2;0) до плоскости:
. Ответ: .
Заключение
Представляю вашему вниманию свою работу, которой я занималась в течение последних месяцев: я искала формулы, подбирала для каждого случая именно те задачи, геометрическое решение которых перегружено формулами, редко используемыми теоремами, сложными преобразованиями и вычислениями.
Конечно, эту работу нельзя считать авторитетным пособием по решению задания 13 ЕГЭ, так как в ней рассмотрено лишь небольшое количество задач, и ограниченное количество приёмов.
Конечно, я не настаиваю на том, что все задачи стереометрии надо решать методом координат, иногда это просто нецелесообразно. Но согласитесь, настолько простое и изящное решение не только освободит время для решения других заданий, но и будет высоко оцениваться проверяющим учителем.
Список использованной литературы
1. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010: Математика /авт.-сост . И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ: Астрель , 2009. – (ФИПИ).
2. Математика. Подготовка к ЕГЭ-2011: учебно-методическое пособие/ под ред. Ф.Ф.Лысенко, С.Ю.Калабухова. – Ростов-на-Дону: Легион – М., 2010.
3. Единый государственный экзамен 2010. Математика. Универсальные материалы для подготовки учащихся / ФИПИ – М.: Интеллект -Центр, 2010.
4. Большая универсальная школьная энциклопедия/ гл. редактор М.Аксёнова – М.: Мир энциклопедий Аванта+, Астрель, 2008.
5. www.fmclass.ru – образовательный портал «Физ/мат класс»
6. www.mathege.ru – открытый банк заданий.
7. www.problems.ru – каталог задач.
