Нахождение угла между векторами: онлайн калькулятор
Два вектора всегда образуют угол. Чтобы найти угол между двумя векторами на плоскости или в пространстве, нужно использовать формулу для скалярного произведения и знать длины векторов. Сначала вычисляется косинус угла между векторами, затем находится и сам угол.
Чтобы найти угол между векторами онлайн, не нужно самостоятельно производить громоздкие вычисления. Достаточно просто задать два вектора в удобной форме (точки или координаты) и нажать кнопку «рассчитать».
Как найти угол между векторами без онлайн калькулятора
Для нахождения угла между векторами используется формула:
cosα=a→*b→|a→||b→|
Приведем пример вычисления угла между двумя векторами на плоскости. Пусть заданы векторы a(3; 4) и b(4; 3). Вычислим скалярное произведение и длины этих векторов, а затем применим формулу для косинуса угла между векторами:
a→*b→=3*4+4*3=12+12=24|a→|=32+42=9+16=25=5|b→|=42+32=16+9=25=5cosα=245*5=2425=0,96
Теперь вычислим арккосинус 0,96 и найдем угол между векторами:
α=arccos(0,96)≈16,3
Проверим вычисления на онлайн-калькуляторе и убедимся в правильности решения.
Онлайн калькулятор вычисления угла между векторами будет полезен ученикам старших классов, студентам и даже преподавателям. Он помогает не только сэкономить время, но и способствует глубинному пониманию примеров, так как каждое действие при вычислении угла между векторами онлайн расписывается максимально подробно.


Калькулятор онлайн.
Вычисление угла между векторами.
Этот калькулятор онлайн вычисляет угол между векторами в двух- или трехмерном пространстве.
Онлайн калькулятор для вычисления угла между векторами не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Определение и основные свойства скалярного произведения векторов
Определение
Скалярным произведением двух ненулевых векторов ( vec{a} ) и ( vec{b} ) называется число (скаляр), равное произведению длин
этих векторов на косинус угла между ними. Если хотя бы один из векторов ненулевой, то угол не определен и скалярное произведение векторов
по определению полагают равным нулю.
Скалярное произведение векторов ( vec{a} ) и ( vec{b} ) обозначают ( vec{a} cdot vec{b} ). Итак,
( vec{a} cdot vec{b} = |vec{a}||vec{b}|cos varphi )
где ( varphi ) – угол между векторами ( vec{a} ) и ( vec{b} )
Типичным примером скалярного произведения векторов в физике является формула работы:
( A = |vec{a}||vec{b}|cos varphi )
где вектор ( vec{a} ) – сила, точка приложения которой перемещается из начала в конец вектора ( vec{b} )
Рассмотрим некоторые свойства скалярного произведения векторов.
1. ( vec{a} cdot vec{b} = vec{b} cdot vec{a} ) (свойство перестановочности сомножителей)
2. ( (alpha vec{a} ) cdot vec{b} = alpha ( vec{b} cdot vec{a} ) ) (свойство сочетательности относительно умножения на число)
3. ( vec{a} cdot ( vec{b} + vec{c} ) = vec{a} cdot vec{b} + vec{a} cdot vec{c} ) (свойство распределительности суммы векторов)
4. ( vec{a} cdot vec{a} = |vec{a}|^2 )
5. ( vec{a} cdot vec{b} = 0 ), если ( vec{a} bot vec{b} ) , и обратно, ( vec{a} bot vec{b} ) ,
если ( vec{a} cdot vec{b} = 0 ) и ( vec{a} neq vec{0}, ; vec{b} neq vec{0} ).
Выражение скалярного произведения через координаты векторов
Теорема
Если векторы ( vec{a} ) и ( vec{b} ) заданы своими координатами:
( vec{a} left( a_x; a_y; a_z right), ;; vec{b} left( b_x; b_y; b_z right) ), то их скалярное произведение можно
вычислить по формуле
( vec{a} cdot vec{b} = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z )
Следствие
Необходимым и достаточным условием перпендикулярности векторов ( vec{a} left( a_x; a_y; a_z right) ) и
( vec{b} left( b_x; b_y; b_z right) ) является равенство
( a_x cdot b_x + a_y cdot b_y + a_z cdot b_z = 0 )
Следствие
Косинус угла между векторами ( vec{a} left( a_x; a_y; a_z right) ) , и ( vec{b} left( b_x; b_y; b_z right) ) определяется
равенством
$$ cos varphi = frac{ vec{a} cdot vec{b}}{ |vec{a}| |vec{b}| } =
frac{a_x cdot b_x + a_y cdot b_y + a_z cdot b_z}{sqrt{a_x^2 + a_y^2 + a_z^2} ; sqrt{b_x^2 + b_y^2 + b_z^2} } $$
Векторы – одна из тем школьной программы. При вычислении угла между векторами можно использовать специальный калькулятор. Это онлайн-сервис, которым могут воспользоваться клиенты фриланс-биржи «Напишем». Он поможет ускорить процесс решения задач или проверить правильность выполнения заданий.
Особенности сервиса
Известно, то между векторами всегда образуется угол. Чтобы его вычислить, нужно знать длины векторов и использовать формулу для определения их скалярного произведения. Процедура состоит из двух действий. Определяется:
- косинус угла между векторами;
- сам угол.
Схематически угол между векторами изображают так:
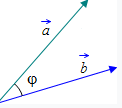
Формула определения скалярного произведения выглядит так:
[ vec{a} cdot vec{b}=|vec{a}| cdot|vec{b}| cdot cos (varphi) ]
Косинус определяется по формуле:
[ cos (varphi)=frac{vec{a} cdot vec{b}}{|vec{a}| cdot|vec{b}|} ]
Используя координатные соотношения, для вычисления косинуса угла между векторами используют следующую формулу:
[ cos (varphi)=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}} ]
Где [vec{a}=left{a_{x}, a_{y}, a_{z}right}] и [vec{b}=left{b_{x}, b_{y}, b_{z}right}].
Чтобы получить нужно е значение, данные подставляют в соответствующие окошки и нажимают клавишу «Решение».
Угол между векторами онлайн
Угол между векторами
– наглядно изображен на рисунке:
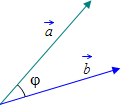
Вычислить его можно исходя из формулы
скалярного произведения векторов:
Тогда:
Если от векторных соотношений перейти к координатным, то формула для вычисления косинуса угла между векторами, примет вид:
, где
и
.
Наш онлайн калькулятор позволяет вычислить угол между векторами с описанием подробного хода решения на русском языке.
Калькулятор угла между векторами
Способ ввода выражения::
Размерность векторов:
Формат задания вектора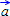 по:
по:
Формат задания вектора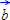 по:
по:
Найти угол между векторомa12и векторомb543т.е.:φa,b-?
Вектор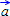 = { }
= { }
Вектор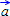
Вектор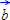 = { }
= { }
Вектор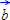
Установить калькулятор на свой сайт
Оставить свой комментарий:
Термин угол между векторами подразумевает наименьший угол между векторами, один из которых нужно вращать до получения сонаправленности с другим. В инженерных, электротехнических и математических расчетах угол между векторами выражается через cos α равный отношению перемноженных скалярных значений a и b на произведение модулей векторов |a| и |b|.
Модули находятся через извлечение корня из суммы квадратов значений координат векторов. Пример: определения угла между векторами с координатами a = {3; 4} и b = {4; 3}.
Скалярное произведение 3 х 4 + 4 х 3 = 24,
|a| = корень (3 в квадрате + 4 в квадрате) = 5,
|b| = корень (4 в квадрате + 3 в квадрате) = 5,
cos α = 0,96.
Онлайн калькулятор позволяет находить углы между векторами не только в двухмерном, но и в трехмерном пространстве. Результирующая информация выдается как в градусах, так и в радианах.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

