iSopromat.ru

Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
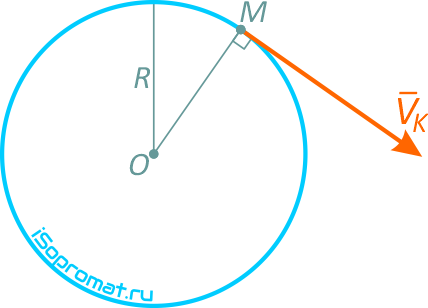
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
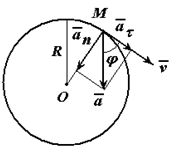
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
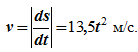

Подставляя в это выражение значение скорости, получим 6=13,5t1 2 , откуда находим
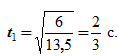
Касательное ускорение для любого момента времени равно
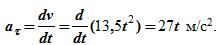
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
Модуль вектора полного ускорения точки равен
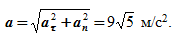
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
Угол между векторами.

Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/vector/angl/
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
[/spoiler]
Вектор
ускорения a
принято раскладывать на две составляющие
– касательную at
(вдоль
вектора скорости v
по касательной к траектории) и нормальную
an
(вперпендикулярном
направлении),: a=at+an,
a=rad(a2t+a2n)
где at=
at
t;
a
n
= an
n;
at
–
тангенциальное
ускорение;
an
–
нормальное
(центростремительное)
ускорение.
При
этом
at
=
a
cos(фи)
, an
=
a sin(фи).
Единичный
вектор
касательной t
направлен по касательной к траектории
движения точки, единичный вектор
главной нормали n
к траектории направлен к центру кривизны.
Тангенциальное at
и
нормальное an
ускорения
характеризуют соответственно изменение
скорости по величине (по модулю) и
изменение направления вектора скорости
точки: at
=dv/dt,
an
=
v2/R
(везде
t
это тау). Угол фи – это угол между
скоростью и ускорением.
Unit Converter
Enter the vector coordinate values of the velocity and acceleration into the calculator to determine the angle between them.
- Vector Subtraction Calculator
- Vector Length Calculator
- Resultant Vectors – The Complete Guide + Calculator
- Unit Vector Calculator
The following formula is used to calculate the angle between two vectors.
A= acos[(a (dot) b) / (||A||*||B||)]
- Where A is the angle between the vectors
- a (dot) b is the dot product between the two vectors
- ||A|| is the magnitude of vector A
- ||B|| is the magnitude of vector B
To calculate the angle between the acceleration and velocity vectors, calculate the dot product of the two vectors, then divide by the product of the magnitudes of each vector.
What are velocity and acceleration vectors?
Definition:
Velocity and acceleration vectors are 3-Dimensional representations of the physical properties of velocity and acceleration.
How to calculate the angle between velocity and acceleration vectors?
Example Problem:
The following example outlines how to calculate the angle between a velocity and acceleration vector.
First, determine the velocity vector. For this example, the velocity vector is (1,2,3).
Next, determine the magnitude of the velocity vector. This is equal to 3.741.
Next, determine the acceleration vector. For this problem, the acceleration is (4,5,6).
Next, calculate the magnitude of the vector. This is 8.7749.
Finally, calculate the angle between the vectors using the formula above:
A= acos[(a (dot) b) / (||A||*||B||)]
A= acos[(32) / 32.87]
A = 13.211 degrees

Диск радиусом 10 см вращается с угловым ускорением, равным ![]() рад/с2. Сколько оборотов сделает диск при изменении частоты вращения от 2.0 оборотов в секунду до 4.0 оборотов в секунду? Найти время
рад/с2. Сколько оборотов сделает диск при изменении частоты вращения от 2.0 оборотов в секунду до 4.0 оборотов в секунду? Найти время ![]() , в течение которого это произойдет. Определить нормальное и тангенциальное ускорения точек на окружности диска в момент времени
, в течение которого это произойдет. Определить нормальное и тангенциальное ускорения точек на окружности диска в момент времени ![]() . Определить угол между векторами скорости и ускорения в тот момент времени, когда диск вращался с частотой 0.5 оборотов в секунду.
. Определить угол между векторами скорости и ускорения в тот момент времени, когда диск вращался с частотой 0.5 оборотов в секунду.
Решение:
Так как угловое ускорение постоянно, используем формулы равноускоренного вращения (21) – (22). Первое соотношение в (21) с учетом (24) сразу дает искомое время ![]() :
:
![]()
использованы данные условия задачи ![]() ,
, ![]() . Полученное время
. Полученное время ![]() можно просто подставить во второе соотношение (21) для нахождения угла поворота
можно просто подставить во второе соотношение (21) для нахождения угла поворота ![]() , а с учетом (23) – и числа оборотов
, а с учетом (23) – и числа оборотов ![]() :
:
![]()
Правильнее будет подставить полученное выше выражение ![]() в приведенную зависимость
в приведенную зависимость ![]() , исключив время
, исключив время ![]() и выразив ответ через данные условия задачи. В результате этой процедуры получим формулу (22):
и выразив ответ через данные условия задачи. В результате этой процедуры получим формулу (22):
![]()
Тангенциальное ускорение согласно (19) оказывается постоянным
![]()
Для определения нормального ускорения по формуле (20) следует найти угловую скорость ![]() в момент времени
в момент времени ![]() с помощью (21):
с помощью (21):
![]()
![]()
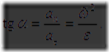
Угол ![]() между векторами скорости
между векторами скорости ![]() и ускорения
и ускорения ![]() можно найти, используя векторы
можно найти, используя векторы ![]() и
и ![]() . Тангенциальное ускорение
. Тангенциальное ускорение ![]() направлено по касательной к окружности, т.е. так же, как и скорость
направлено по касательной к окружности, т.е. так же, как и скорость ![]() . Поэтому (см. рис. 9)
. Поэтому (см. рис. 9)
Подставляя сюда ![]() , где
, где ![]() и
и ![]() , получаем
, получаем
![]()


Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t3 (s в метрах, t в секундах).
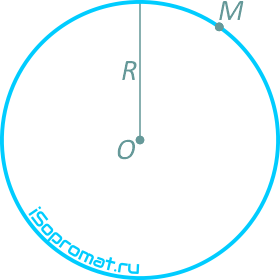
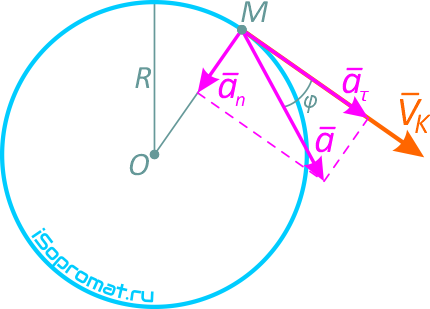
Рисунок 1.6
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Другие примеры решений >
Помощь с решением задач >
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
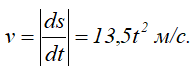
Другие видео
Скорость точки направлена по касательной к траектории (окружности), т.е. перпендикулярно линии радиуса.
Подставляя в предыдущее выражение значение скорости, получим 6=13,5t12, откуда находим
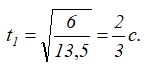
Касательное ускорение для любого момента времени равно
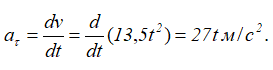
При t=t1=2/3 с
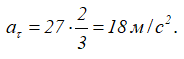
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
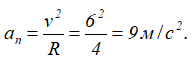
Модуль вектора полного ускорения точки равен
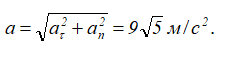
Направление нормального, касательного и полного ускорений точки
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
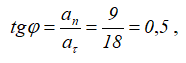
отсюда
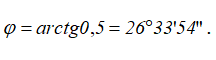
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
