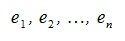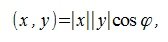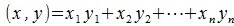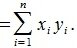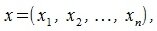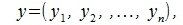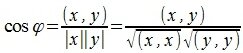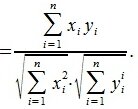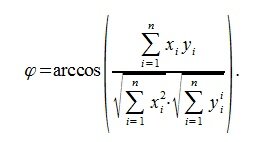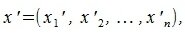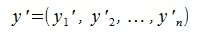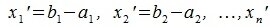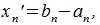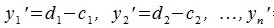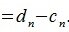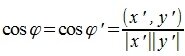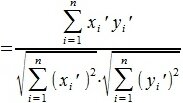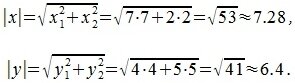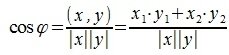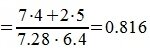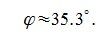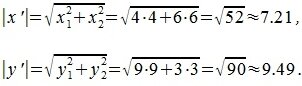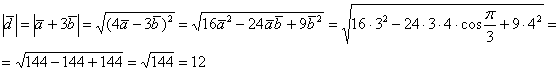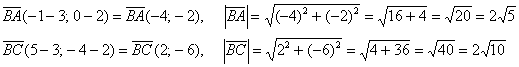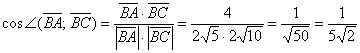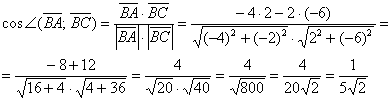Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Угол между двумя векторами
Пусть в n-мерном пространстве задан ортонормированный базис
Как известно скалярное произведение ненулевых векторов x и y называется произведение
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
И, следовательно, угол между двумя векторами будет равен
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x= AB и y= CD, где 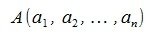
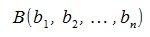
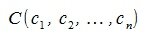
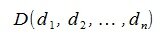
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками):
При таком перемещении угол между векторами x и y равен углу между векторами x’ и y’. Следовательно косинус угла между двумя векторами равен:
Угол между двумя векторами будет равен:
Примеры вычисления угла между двумя векторами
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
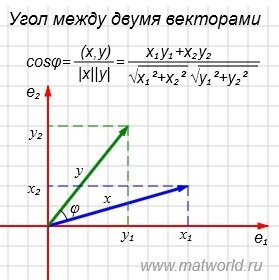
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
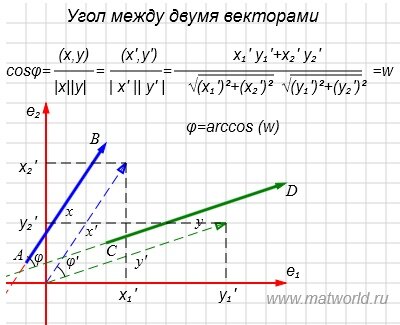
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
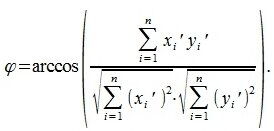
Косинус угла между векторами x и y, будет равен:
Из выражения (5) вычисляем угол φ:
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x= AB и y= CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x= AB и y= CD.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x’ и y’ с координатами (т.е. с конечными точками): x’=(3-(-1),7-1)=(4,6), y’=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ’ между векторами x’ и y’. Поэтому вычисляя угол φ’ , получим угол между векторами x и y.
Вычислим норму векторов x’ и y’:
Косинус угла между векторами x’ и y’:
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://matworld.ru/vector/angle-between-vectors.php
[/spoiler]
Угол между векторами

Если
известны длины двух векторов и их
скалярное произведение, то можно
вычислить косинус угла между данными
векторами, а, следовательно, и сам угол.
.
Пример
Найти
угол между векторами
и
,
если известно, что
.
Решение: Используем
формулу:
На
заключительном этапе вычислений
использован технический приём –
устранение иррациональности в знаменателе.
В целях устранения иррациональности я
домножил числитель и знаменатель на
.
Итак,
если
,
то:
Ответ:
Не
забываем указывать размерность –
радианы и градусы.
Пример
Даны
–
длины векторов
,
и
угол между ними
.
Найти угол между векторами
,
.
Алгоритм
решения:
1)
По условию требуется найти угол между
векторами
и
,
поэтому нужно использовать формулу
.
2)
Находим скалярное произведение
.
3)
Находим длину вектора
и
длину вектора
.
4)
Нам известно число
,
а значит, легко найти и сам угол: 
Сделайте
самостоятельно и сравните с решением.
Решение:
Найдём скалярное произведение:
Найдём
длину вектора
:
Найдём
длину вектора
:
Таким
образом:
Ответ:
Скалярное произведение векторов, заданных координатами в ортонормированном базисе
В
данном разделе рассматриваются только
ортонормированные базисы плоскости
и пространства.
Скалярное
произведение векторов
и
,
заданных в ортонормированном
базисе
, выражается
формулой
Скалярное
произведение векторов
,
заданных в ортонормированном
базисе
, выражается
формулой
То
есть, скалярное произведение равно
сумме произведений соответствующих
координат векторов.
Пример
Найти
скалярное произведение
векторов:
а)
и
б)
и
,
если даны точки
Решение:
а)
Здесь даны векторы плоскости. По
формуле
:
б)
Сначала найдём векторы:
По
формуле
вычислим
скалярное произведение:
Ответ:
Проверка векторов на ортогональность с помощью скалярного произведения
Векторы
и
ортогональны
тогда и только тогда, когда
.
В координатах данный факт запишется
следующим образом:
(для
векторов плоскости);
(для
векторов пространства).
Пример
а)
Проверить ортогональность векторов:
и
б)
Выяснить, будут ли перпендикулярными
отрезки
и
,
если
Решение:
а)
Вычислим их скалярное произведение:
,
следовательно,
б)
Найдём векторы:

Вычислим
их скалярное произведение:
,
значит, отрезки
и
не
перпендикулярны.
Ответ: а)
,
б) отрезки
не
перпендикулярны.
Формула косинуса угла между векторами, которые заданы координатами
Косинус
угла между векторами плоскости
и
,
заданными в ортонормированном
базисе
, выражается
формулой:
.
Косинус
угла между векторами пространства
,
заданными в ортонормированном
базисе
, выражается
формулой:
Пример
Даны
три вершины треугольника
.
Найти
(угол
при вершине
).
Решение:
Требуемый
угол
помечен
дугой. Угол
треугольника
совпадает с углом между векторами
и
,
иными словами:
.
Найдём
векторы:

Вычислим
скалярное произведение:
И
длины векторов:
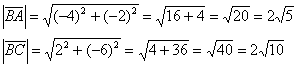
Косинус
угла:

Найдём
сам угол:
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1.6.9. Как найти угол между векторами в координатах?
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса
угла между векторами выразить через
координаты векторов :
Косинус угла между векторами плоскости и
,
заданными в ортонормированном базисе , выражается формулой:
.
Косинус угла между векторами пространства , заданными в ортонормированном базисе
, выражается формулой:
Возвращаемся к нашим треугольникам:
Задача 31
Даны три вершины треугольника . Найти
.
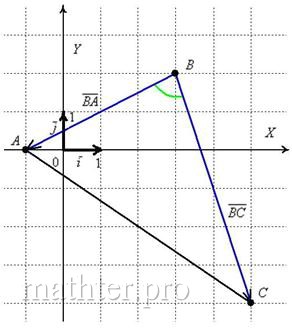
Решение: по условию чертёж выполнять не требуется, но всё-таки:
Из чертежа совершенно очевидно, что угол треугольника совпадает с углом между векторами
и
, иными словами:
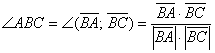
Вычислим скалярное произведение:
Таким образом:
Именно такой порядок выполнения задания рекомендую «чайникам». Более подготовленные читатели могут записать вычисления
«одной строкой»:
Косинус получился «плохим» (не табличным), однако, это не окончательный ответ задачи, и поэтому, к слову, не имеет особого
смысла избавляться от корня в знаменателе.
Найдём сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки можно использовать Алгебраический
Калькулятор (см. Приложения) или даже измерить угол транспортиром (у кого он есть). Только не
повредите покрытие монитора =)
Ответ:
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем
указать точный ответ: и приближенное значение
угла: , найденное с помощью
калькулятора.
Задача 32
В пространстве задан треугольник координатами своих вершин ,
.
Найти угол между сторонами и
Это пример для самостоятельного решения, и, конечно же, задачка творческая, повторяем взаимосвязь между углом и знаком скалярного произведения:
Задача 33
При каком значении угол между векторами
будет: а) острым, б) прямым, в) тупым?
Решение и ответ в конце книги.
Следующий небольшой параграф будет посвящен ортогональным проекциям векторов, в которых тоже «замешано» скалярное произведение:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Пример 2. Найти угол между векторами a = {7; 1} и b = {5; 5}.
Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2
|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Пример 4. Найти угол между векторами a = {1; 0; 3} и b = {5; 5; 0}.
Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10
|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
cos α =
a · b|a| · |b|
=
5√10 · 5√2
=
12√5
=
√510
= 0.1√5
Угол между векторами – теория и примеры нахождения
Угол между векторами a и b – это тот угол, который находится между лучами и может получаться от 0 до 180 градусов. Как правило, угол находится при помощи скалярного произведения векторов или благодаря теореме косинуса для треугольника.
Угол между векторами – теория и примеры нахождения обновлено: 16 апреля, 2020 автором:
Помощь в написании работы
Угол между векторами
Рассмотрим, как получается угол между векторами. Пусть заданы ненулевые векторы и
. Соединим эти векторы с общей точкой
и в направлениях векторов
и
проведём с точки
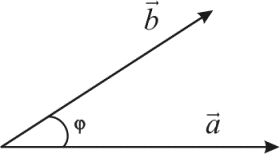
лучи (см. рис. 1)
Рис. 1
Угол между вектором и нулевым вектором не обозначается.
Очевидно, что если , тогда
^
=
. Если же
, тогда
^
=
.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры нахождения угла между векторами
В теме разобрались и теперь осталось закрепить её при помощи нескольких примеров.
Найти угол между векторами и
Решение:
Находим модели векторов:
Находим угол между векторами:
=
=
=
Угол между векторами – теория и примеры нахождения обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру