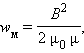Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:
$frac<Delta text<Ф>><Delta t>$ ― скорость изменения магнитного потока [Вб/с],
∆t ― время, за которое происходит это изменение [c].
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции $varepsilon_i = -frac<Delta text<Ф>><Delta t>$
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text<Ф>_t’$
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text<Ф>_t’$
Подставив сюда значение производной, получим $varepsilon_i = -text<Ф>_t’$ = abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома $I = frac<varepsilon>$ , подставив сюда значение ЭДС, получаем $I = frac$.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_ = frac$.
Отсюда можно легко выразить площадь контура $S = fracR>$, подставив сюда все значения, получим $S = fracR> = frac <35cdot 10^<-3>Acdot 1,2text<Ом>><6cdot 10^<-3>text <Тл>cdot 35000c^<-1>> = 0,002text<м>^2$
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
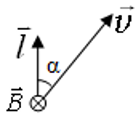
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;
α ― угол между направлением вектора скорости $overrightarrow$ и длиной проводника $overrightarrow$ , если вектор индукции магнитного поля $overrightarrow$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow perp overrightarrow, overrightarrow perp overrightarrow$
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
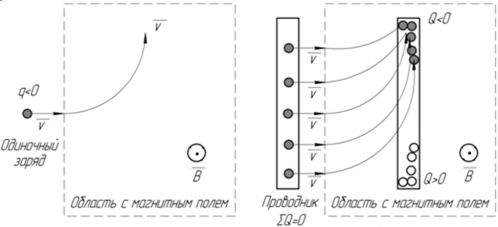
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
U — разность потенциалов [В],
v — скорость движения проводника $big[ frac<text<м>> big]$
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac<Delta text<Ф>><Delta t>$
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.
Задача 3
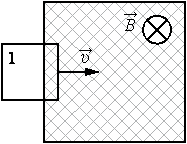
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
Решение:
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
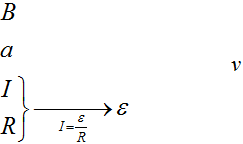
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
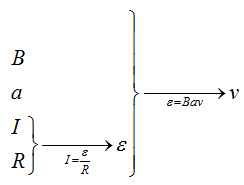
Пройдёмся вдоль этой цепочки.
Запишем закон Ома $I = frac<varepsilon>$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac<varepsilon> = frac$отсюда выразим скорость, и, подставив все величины, получим $v = frac = frac <1cdot 10^<-3>Acdot 10text<Ом>> <0,1 text<Тл>cdot 0,1 text<м>> = 1 frac<text<м>>$
Физика. 11 класс
Конспект урока
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» – правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. – М: Дрофа, 2009. – С.109 – 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
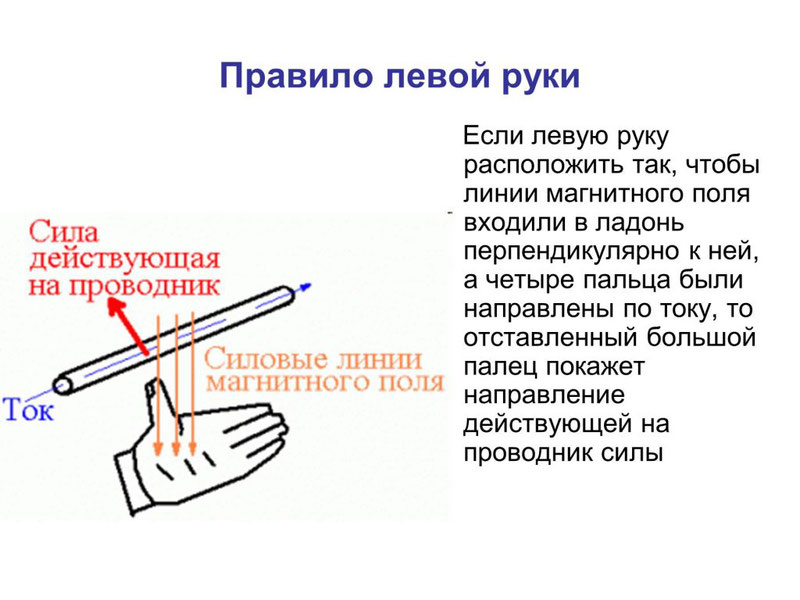
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 0 большой палец покажет направление силы Ампера.
Сила Ампера – сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 90 0 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
– точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 90 0 большой палец покажет направление силы Ампера, т. е. она направлена влево.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10 – ¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
Запишем формулу модуля магнитной индукции:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Запишем формулу силы Ампера:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
Найти:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
[spoiler title=”источники:”]
http://reshutest.ru/theory/13?theory_id=343
http://resh.edu.ru/subject/lesson/3806/conspect/
[/spoiler]
Тема: Определить угол между направлениями тока и вектором магнитной индукции (Прочитано 9251 раз)
0 Пользователей и 1 Гость просматривают эту тему.
4. 16. В однородном магнитном поле с индукцией B = 0,2 Тл находится прямой проводник длиной l = 15 см, по которому течёт ток I = 5 А. На проводник действует сила F = 0,13 H. Определить угол α между направлениями тока и вектором магнитной индукции. Ответ: 60°. Сделать рисунок.

Записан
Решение.
На проводник, с током помещенный в магнитное поле действует сила Ампера. Направление воздействия силы Ампера на проводник с током определяем по правилу левой руки так: если расположить левую руку так, чтобы силовые вектора магнитной индукции были направлены в ладонь, а пальцы ладони были вытянуты по направлению тока, то отведенный под 90 градусов большой палец укажет направление силы Ампера.
[ begin{align}
& {{F}_{A}}=Icdot Bcdot lcdot sin alpha ,sin alpha =frac{{{F}_{A}}}{Icdot lcdot B} (1); sin alpha =frac{0,13}{5cdot 0,15cdot 0,2}=0,866. \
& alpha =frac{pi }{3}. \
end{align} ]
« Последнее редактирование: 14 Сентября 2016, 14:47 от alsak »

Записан
Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью  к площади контура и вектором индукции магнитного поля
к площади контура и вектором индукции магнитного поля  .
.
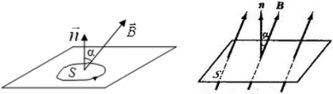
Если вектор индукции магнитного поля  перпендикулярен площади контура, то магнитный поток равен:
перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
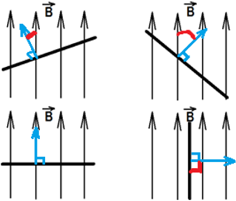
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором  и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

где:
 ― ЭДС электромагнитной индукции [B],
― ЭДС электромагнитной индукции [B],
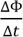 ― скорость изменения магнитного потока [Вб/с],
― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:

где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции 
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени 
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобочках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
 .
.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что 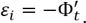
Подставив сюда значение производной, получим  = abS · sin (bt).
= abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома  , подставив сюда значение ЭДС, получаем
, подставив сюда значение ЭДС, получаем 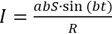 .
.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет своё значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, 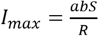 .
.
Отсюда можно легко выразить площадь контура  , подставив сюда все значения, получим
, подставив сюда все значения, получим 
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
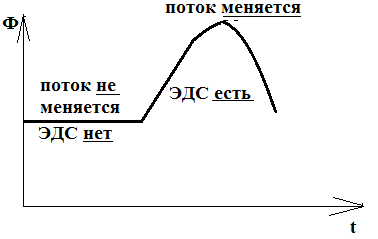
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
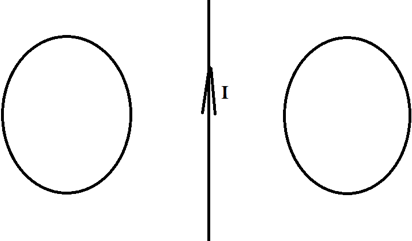
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
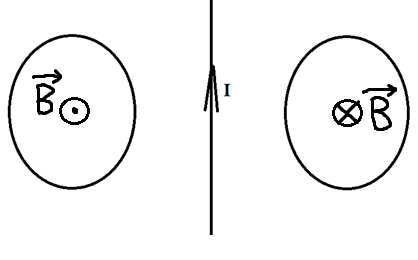
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
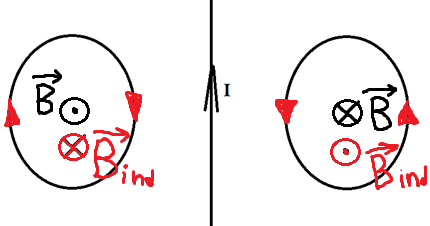
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС  ;
;
где:
 ― ЭДС электромагнитной индукции [B],
― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости 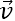 и длиной проводника
и длиной проводника  , если вектор индукции магнитного поля
, если вектор индукции магнитного поля 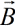 перпендикулярен проводнику и вектору скорости его движения:
перпендикулярен проводнику и вектору скорости его движения: 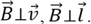

Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создает ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника 
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нём возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу 
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу  =U= lvBsinα.
=U= lvBsinα.
Задача 3
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
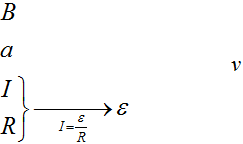
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
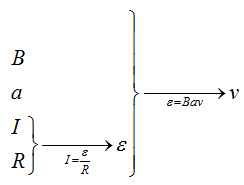
Пройдёмся вдоль этой цепочки.
Запишем закон Ома  , подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим
, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим  отсюда выразим скорость, и, подставив все величины, получим
отсюда выразим скорость, и, подставив все величины, получим 
Ответ: 1
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
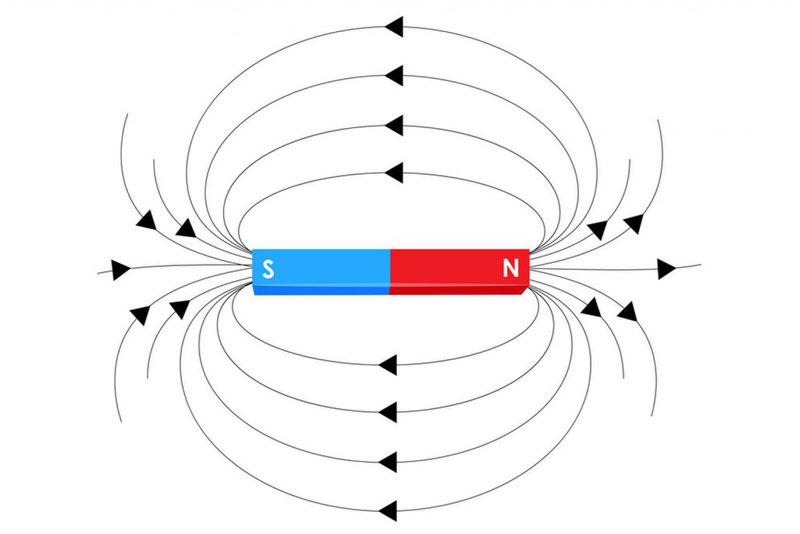
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
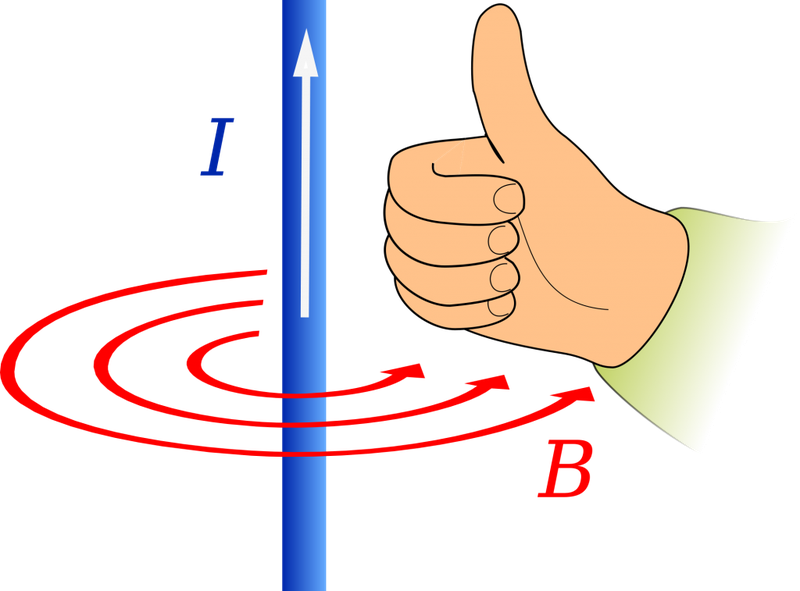
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
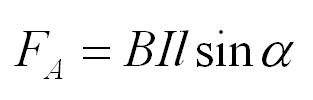
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
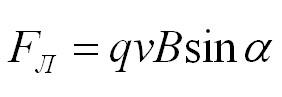
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
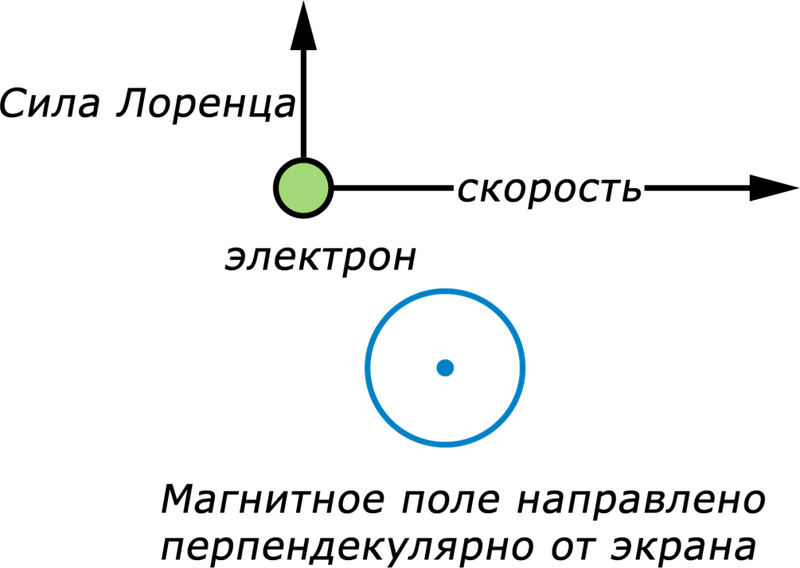
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
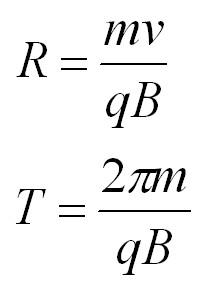
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
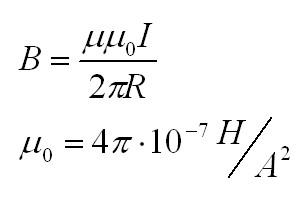
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
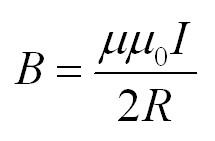
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
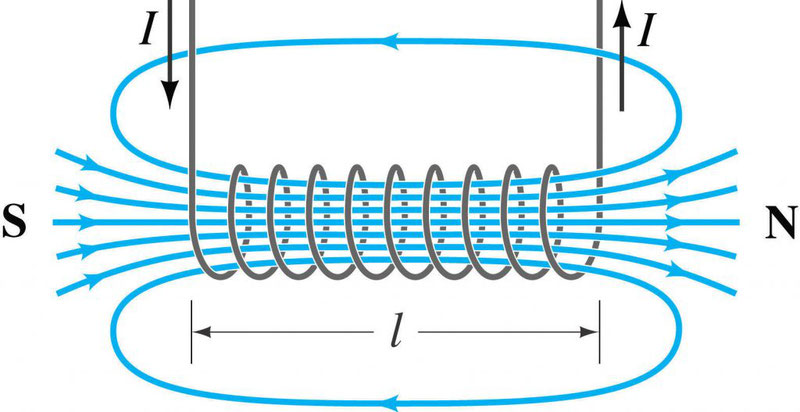
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
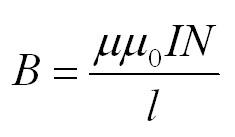
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
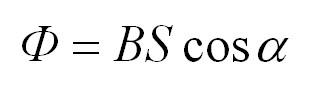
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
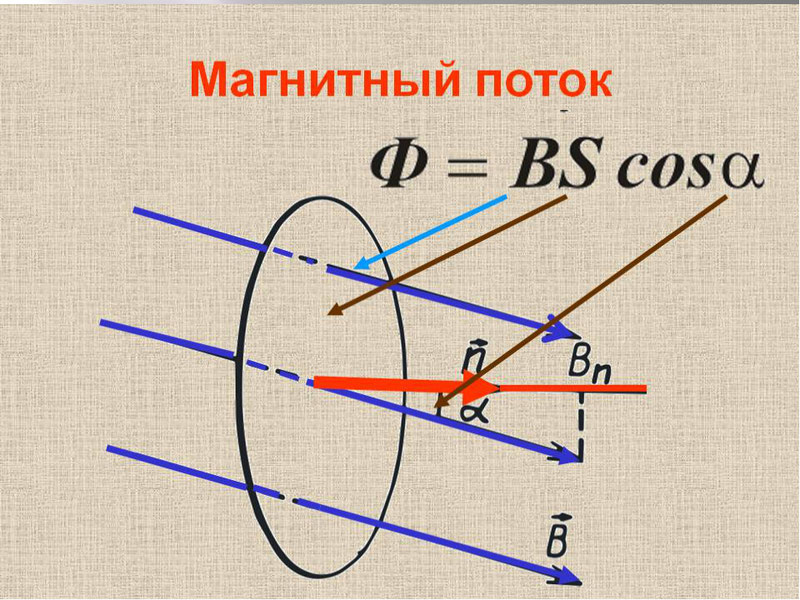
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
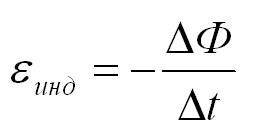
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
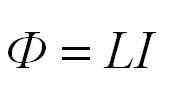
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
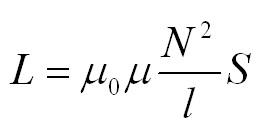
Формула для ЭДС самоиндукции:
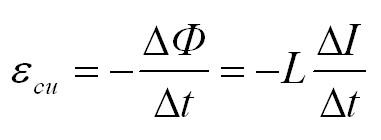
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
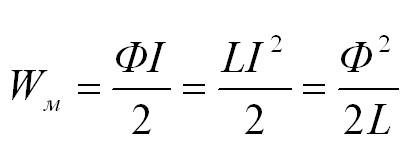
Объемная плотность энергии поля:
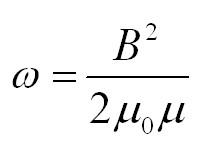
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.
-
Электромагнитное
поле, особая
форма материи, посредством которой
осуществляется взаимодействие между
электрически заряженными частицами
(см. Поля физические). Электромагнитное
поле в вакууме характеризуется вектором
напряжённости электрического поля Е
и магнитной индукцией В, которые
определяют силы, действующие со стороны
поля на неподвижные и движущиеся
заряженные частицы. Наряду с векторами
Е и В, измеряемыми непосредственно,
Электромагнитное поле может
характеризоваться скалярным j и векторным
А потенциалами, которые определяются
неоднозначно, с точностью до градиентного
преобразования (см. Потенциалы
электромагнитного поля). В среде
Электромагнитное поле характеризуется
дополнительно двумя вспомогательными
величинами: напряжённостью магнитного
поля Н и электрической индукцией D (см.
Индукция электрическая и магнитная).
Поведение
Электромагнитное поле изучает классическая
электродинамика, в произвольной среде
оно описывается Максвелла уравнениями,
позволяющими определить поля в зависимости
от распределения зарядов и токов.
Микроскопические Электромагнитное
поле, созданные отд. элементарными
частицами, характеризуются напряжённостями
микроскопических полей: электрического
поля е и магнитного h. Их средние значения
связаны с макроскопическими характеристиками
Электромагнитное поле следующим образом:
, . Микроскопические поля удовлетворяют
Лоренца — Максвелла уравнениям.
Электромагнитное
поле неподвижных или равномерно
движущихся заряженных частиц неразрывно
связано с этими частицами; при ускоренном
движении частиц Электромагнитное поле
«отрывается» от них и существует
независимо в форме электромагнитных
волн.
Порождение
Электромагнитное поле переменным
магнитным полем и магнитного поля —
переменным электрическим приводит к
тому, что электрические и магнитные
поля не существуют обособленно, независимо
друг от друга. Компоненты векторов,
характеризующих Электромагнитное поле,
образуют, согласно относительности
теории, единую физ. величину — тензор
Электромагнитное поле, компоненты
которого преобразуются при переходе
от одной инерциальной системы отсчёта
к другой в соответствии с Лоренца
преобразованиями.
При
больших частотах Электромагнитное поле
становятся существенными его квантовые
(дискретные) свойства. В этом случае
классическая электродинамика неприменима
и Электромагнитное поле описывается
квантовой электродинамикой.
Магни́тная
инду́кция
![]()
— векторная величина, являющаяся силовой
характеристикой магнитного поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с какой
силой
![]()
магнитное поле действует на заряд
![]()
, движущийся со скоростью
![]()
.
Более
конкретно,
— это такой вектор, что сила Лоренца
, действующая со стороны магнитного
поля[1] на заряд
,
движущийся со скоростью
![]()
, равна
![]()
![]()
α
— угол между векторами скорости и
магнитной индукции (направление вектора
перпендикулярно им обоим и направлено
по правилу буравчика).
Также
магнитная индукция может быть определена[2]
как отношение максимального механического
момента сил, действующих на рамку с
током, помещенную в однородное поле, к
произведению силы тока в рамке на её
площадь.
Является основной
фундаментальной характеристикой
магнитного поля, аналогичной вектору
напряжённости электрического поля.
В
системе СГС магнитная индукция поля
измеряется в гауссах (Гс), в системе СИ
— в теслах (Тл)
1
Тл = 10^4 Гс
Магнитометры,
применяемые для измерения магнитной
индукции, называют тесламетрами.
Магни́тный
пото́к —
поток
![]()
как интеграл вектора магнитной индукции
через конечную поверхность
![]()
.
Определяется через интеграл по поверхности

при
этом векторный элемент площади поверхности
определяется как
![]()
где
![]()
— единичный вектор, нормальный к
поверхности.
Также
магнитный поток можно рассчитать как
скалярное произведение вектора магнитной
индукции на вектор площади:
![]()
где
α
— угол между вектором магнитной индукции
и нормалью к плоскости площади.
Магнитный
поток через контур также можно выразить
через циркуляцию векторного потенциала
магнитного поля по этому контуру:
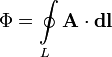
В
СИ единицей магнитного потока является
Вебер (Вб, размерность — В·с = кг·м²·с−2·А−1),
в
системе СГС — максвелл (Мкс); 1 Вб = 10^8
Мкс.
Прибор
для измерения магнитных потоков
называется Флюксметр (от лат. fluxus —
течение и …метр) или веберметр.
В
соответствии с теоремой Гаусса для
магнитной индукции поток вектора
магнитной индукции через любую замкнутую
поверхность равен нулю:
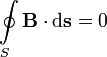
Или,
в дифференциальной форме — дивергенция
магнитного поля равна нулю:
![]()
Это
означает, что в классической электродинамике
невозможно существование магнитных
зарядов, которые создавали бы магнитное
поле подобно тому, как электрические
заряды создают электрическое поле.
-
Закон
Био́—Савара—Лапла́са
— физический закон для определения
вектора индукции магнитного поля,
порождаемого постоянным электрическим
током. Был установлен экспериментально
в 1820 году Био и Саваром и сформулирован
в общем виде Лапласом. Лаплас показал
также, что с помощью этого закона можно
вычислить магнитное поле движущегося
точечного заряда (считая движение одной
заряженной частицы током).
Закон
Био—Савара—Лапласа играет в магнитостатике
ту же роль, что и закон Кулона в
электростатике. Закон Био—Савара—Лапласа
можно считать главным законом
магнитостатики, получая из него остальные
ее результаты.
В
современной формулировке закон
Био—Савара—Лапласа чаще рассматривают
как следствие двух уравнений Максвелла
для магнитного поля при условии
постоянства электрического поля, т.е.
в современной формулировке уравнения
Максвелла выступают как более
фундаментальные (прежде всего хотя бы
потому, что формулу Био—Савара—Лапласа
нельзя просто обобщить на общий случай
полей, зависящих от времени).

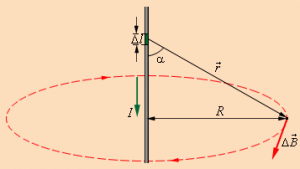
Для
магнитного поля, как и для электрического,
справедлив принцип суперпозиции:
магнитная индукция результирующего
поля, создаваемого несколькими токами
или движущимися зарядами, равна векторной
сумме магнитных индукций складываемых
полей, создаваемых каждым током или
движущимся зарядом в отдельности:
![]()
акон
Био-Савара-Лапласа для некоторых токов:
Магнитное
поле прямого тока
![]()
Магнитное
поле кругового тока :
![]()
В
формуле мы использовали :
-
— Магнитная
индукция
-
— Вектор,
по модулю равный длине dl
элемента проводника и совпадающий по
направлению с током
![]()
— Магнитная
постоянная.
-
— Относительная
магнитная проницаемость (среды)
-
-сила
тока.
R-
Расстояние от
провода до точки, где мы вычисляем
магнитную индукцию
-
— Угол
между вектором dl и r
-
Поток вектора магнитной индукции. Теорема Гаусса для поля в.
Потоком
вектора магнитной индукции (магнитным
потоком) через площадку dS называется
скалярная физическая величина, равная
![]()
где
Bn=В cos a —проекция вектора В на направление
нормали к площадке dS (a — угол между
векторами n и В), dS=dSn — вектор, модуль
которого равен dS, а направление его
совпадает с направлением нормали n к
площадке. Поток вектора В может быть
как положительным, так и отрицательным
в зависимости от знака cos a (определяется
выбором положительного направления
нормали n). Поток вектора В связывают с
контуром, по которому течет ток. В таком
случае положительное направление
нормали к контуру: оно связывается с
током правилом правого винта. Таким
образом, магнитный поток, создаваемый
контуром через поверхность, ограниченную
им самим, всегда положителен.
Поток
вектора магнитной индукции ФB через
произвольную поверхность S равен
![]()
Для
однородного поля и плоской поверхности,
расположенной перпендикулярно вектору
В, Bn=B=const и
![]()
Из
этой формулы определяется единица
магнитного потока вебер (Вб): 1 Вб —
магнитный поток, проходящий сквозь
плоскую поверхность площадью 1 м2,
расположенную перпендикулярно однородному
магнитному полю, индукция которого
равна 1 Тл (1 Вб=1 Тл×м2).
Теорема
Гаусса для поля В: поток вектора магнитной
индукции сквозь любую замкнутую
поверхность равен нулю:
![]()
Эта
теорема отражает факт отсутствия
магнитных зарядов, вследствие чего
линии магнитной индукции не имеют ни
начала, ни конца и являются замкнутыми.
Циркуляцией
вектора
![]()
называют сумму произведений Δl, взятую
по всему контуру L:
![]()
Некоторые
токи, создающие магнитное поле, могут
пронизывать выбранный контур L в то
время, как другие токи могут находиться
в стороне от контура.
Теорема
о циркуляции утверждает, что циркуляция
вектора
магнитного поля постоянных токов по
любому контуру L всегда равна произведению
магнитной постоянной μ0 на сумму всех
токов, пронизывающих контур:
![]()
Простейшим
примером применения
теоремы о циркуляции является вывод
формулы для магнитной индукции поля
прямолинейного проводника с током.
Учитывая симметрию в данной задаче,
контур L целесообразно выбрать в виде
окружности некоторого радиуса R, лежащей
в перпендикулярной проводнику плоскости.
Центр окружности находится в некоторой
точке проводника. В силу симметрии
вектор
направлен по касательной
![]()
, а его модуль одинаков во всех точках
окружности. Применение теоремы о
циркуляции приводит к соотношению:
![]()
откуда
следует формула для модуля магнитной
индукции поля прямолинейного проводника
с током.
Этот
пример показывает, что теорема о
циркуляции вектора магнитной индукции
может быть использована для расчета
магнитных полей, создаваемых симметричным
распределением токов, когда из соображений
симметрии можно «угадать» общую структуру
поля.
-
Соленоид
– проводник,
навитый по винтовой линии на поверхность
цилиндра
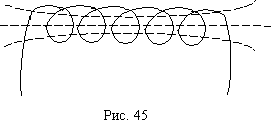
Пусть
по проводнику течет ток . Направление
вектора
![]()
образует с направлением тока правовинтовую
систему внутри соленоида. Обозначим
![]()
– число витков на единицу длины.
Cчитая
шаг малым, можно заменить витки круговыми,
замкнутыми. Пусть сечение проводника
мало, т.е. ток считаем текущим по
поверхности.
вектор
направлен вдоль оси (линии вектора
параллельны, и поле внутри однородно).
Контур
выбираем таким образом, чтобы вдоль
него вектор
был одинаков (рис.46).
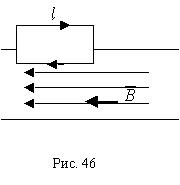
По
теореме о циркуляции
![]()
,
где
![]()
– циркуляция,
![]()
– ток, охватываемый данным контуром,
Тогда
![]()
– внутри соленоида поле однородно (без
учета краевых эффектов).
Тороид
– проводник, навитый на поверхность в
виде тора.
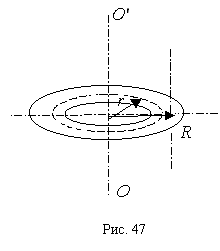
R-
– радиус тора, r
– – радиус контура; N-
число витков.
линии
вектора
– окружности, центры, которых лежат на
оси
![]()
в
качестве контура берем такую окружность.
Если
контур – внутри тороида: он охватывает
ток
![]()
, и по теореме о циркуляции
![]()

При
![]()
и
![]()
–
формула для бесконечно длинного
соленоида.
Вне
тороида: контур токов не охватывает:
![]()
магнитного поля нет.
У
реального тороида линии тока (витки) не
находятся в плоскости, проходящей через
ось
(как принималось в расчете) имеется
дополнительная составляющая тока вдоль
оси, создающая поле, аналогичное полю
кругового тока.
-
Найдем
магнитное поле, создаваемое одним
движущимся зарядом.
Любой
проводник с током создает в окружающем
пространстве магнитное поле. При этом
электрический же ток является упорядоченным
движением электрических зарядов. Значит
можно считать, что любой движущийся в
вакууме или среде заряд попрождает
вокруг себя магнитное поле. В результате
обобщения многочисленных опытных данных
был установлен закон, который определяет
поле В точечного заряда Q, движущегося
с постоянной нерелятивистской скоростью
v. Этот закон задается формулой
![]()
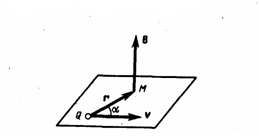
где
r — радиус-вектор, который проведен от
заряда Q к точке наблюдения М (рис. 1).
Согласно (1), вектор В направлен
перпендикулярно плоскости, в которой
находятся векторы v и r : его направление
совпадает с направлением поступательного
движения правого винта при его вращении
от v к r.
Модуль
вектора магнитной индукции (1) находится
по формуле
![]()
где
α — угол между векторами v и r.
Сопоставляя
закон Био-Савара-Лапласа и (1), мы видим,
что движущийся заряд по своим магнитным
свойствам эквивалентен элементу тока:
![]()
Приведенные
законы (1) и (2) выполняются лишь при малых
скоростях (v<<с) движущихся зарядов,
когда электрическое поле движущегося
с постоянной скорость заряда можно
считать электростатическим, т. е.
создаваемым неподвижным зарядом, который
находится в той точке, где в данный
момент времени находится движущийся
заряд.
Формула
(1) задает магнитную индукцию положительного
заряда, движущегося со скоростью v. При
движении отрицательнго заряда Q заменяется
на -Q. Скорость v – относительная скорость,
т. е. скорость относительно системы
отсчета наблюдателя. Вектор В в данной
системе отсчета зависит как от времени,
так и от расположения наблюдателя.
Поэтому следует отметить относительный
характер магнитного поля движущегося
заряда.
Первый,
кто обнаружил поле движущегося заряда,
был американский физик Г. Роуланду
(1848—1901). Окончательно этот факт был
установлен профессором Московского
университета А. А. Эйхенвальдом
(1863—1944), который изучал магнитное поле
конвекционного тока и магнитное поле
связанных зарядов поляризованного
диэлектрика. Магнитное поле движущихся
с постоянной скоростьб зарядов было
измерено академиком А. Ф. Иоффе, который
также доказал эквивалентность, в смысле
возбуждения магнитного поля, электронного
пучка и тока проводимости.
Сила
лоренца.
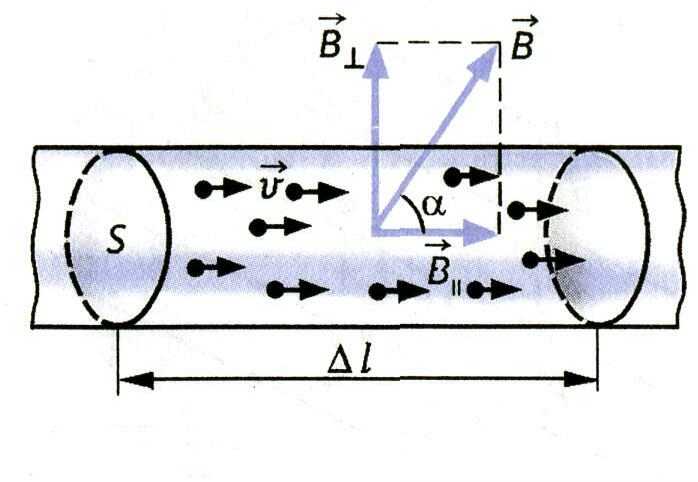
Так
как электрический ток представляет
собой упорядоченное движение зарядов,
то действие магнитного поля на проводник
с током есть результат его действия на
отдельные движущиеся заряды.
Силу,
действующую со стороны магнитного поля
на движущиеся в нем заряды, называют
силой Лоренца.
Сила
Лоренца определяется соотношением:
Fл = q·V·B·sina
где
q – величина движущегося заряда;
V
– модуль его скорости;
B
– модуль вектора индукции магнитного
поля;
a
– угол между вектором скорости заряда
и вектором магнитной индукции.
Обратите
внимание, что сила Лоренца перпендикулярна
скорости и поэтому она не совершает
работы, не изменяет модуль скорости
заряда и его кинетической энергии. Но
направление скорости изменяется
непрерывно.
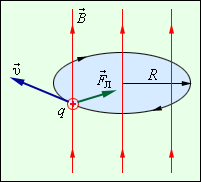
Сила
Лоренца перпендикулярна векторам В и
v , и её направление определяется с
помощью того же правила левой руки, что
и направление силы Ампера: если левую
руку расположить так, чтобы составляющая
магнитной индукции В, перпендикулярная
скорости заряда, входила в ладонь, а
четыре пальца были направлены по движению
положительного заряда (против движения
отрицательного), то отогнутый на 90
градусов большой палец покажет направление
действующей на заряд силы Лоренца F л.
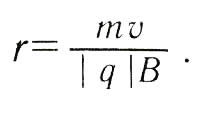
Сила Лоренца зависит
от модулей скорости частицы и индукции
магнитного поля. Эта сила перпендикулярна
скорости и, следовательно, определяет
центростремительное ускорение частицы.
Частица равномерно движется по окружности
радиуса r.
-
Если
к прямолинейному
проводнику с током поднести магнитную
стрелку, то она будет стремиться стать
перпендикулярно плоскости, проходящей
через ось проводника и центр вращения
стрелки (рис. 67). Это указывает на то,
что на стрелку действуют особые силы,
которые называются магнитными. Иными
словами, если по проводнику проходит
электрический ток, то вокруг проводника
возникает м а г н и т н о е поле.
Магнитное
поле можно рассматривать как особое
состояние пространства, окружающего
проводники с током.
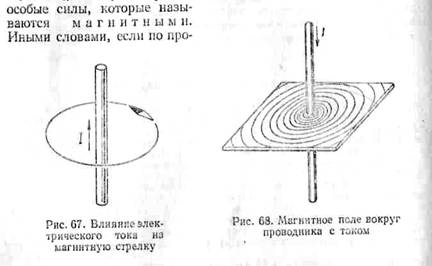
Если
продеть через картон толстый проводник
и пропустить по нему электрический ток,
то стальные опилки, насыпанные на картон,
расположатся вокруг проводника по
концентрическим окружностям, представляющим
собой в данном случае так называемые
магнитные линии (рис. 68). Мы можем
передвигать картон вверх или вниз по
проводнику, но расположение стальных
опилок не изменится. Следовательно,
магнитное поле возникает вокруг
проводника по всей его длине.
Если
на картон поставить маленькие магнитные
стрелки, то, меняя направление тока в
проводнике, можно увидеть, что магнитные
стрелки будут поворачиваться (рис. 69).
Это показывает, что направление магнитных
линий меняется с изменением направления
тока в проводнике.
Магнитное
поле вокруг проводника с током обладает
следующими особенностями: магнитные
линии прямолинейного проводника имеют
форму концентрических окружностей;
чем ближе к проводнику, тем плотнее
располагаются магнитные линии, тем
больше магнитная индукция; магнитная
индукция (интенсивность поля) зависит
от величины тока в проводнике; направление
магнитных линий зависит от направления
тока в проводнике.
Чтобы
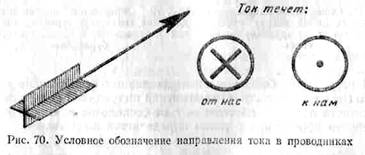
показать направление тока в проводнике,
изображенном в разрезе, принято условное
обозначение, которым мы в дальнейшем
будем пользоваться. Если мысленно
поместить в проводнике стрелу по
направлению тока (рис. 70), то в проводнике,
ток в котором направлен от нас, увидим
хвост оперения стрелы (крестик);
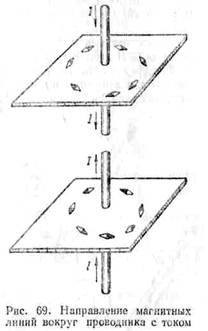
если же ток
направлен к нам, увидим острие стрелы
(точку).
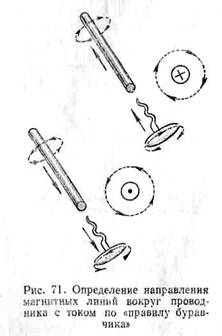
Направление
магнитных линий вокруг проводника с
током можно определить по «правилу
буравчика». Если буравчик (штопор) с
правой резьбой будет двигаться
поступательно по направлению тока, то
направление вращения ручки будет
совпадать с направлением магнитных
линий вокруг проводника (рис. 71).
Магнитная
стрелка, внесенная в поле проводника с
током, располагается вдоль магнитных
линий. Поэтому для определения ее
расположения можно также воспользоваться
«правилом буравчика» (рис. 72).
Магнитное
поле есть одно из важнейших проявлений
электрического тока и не может быть
получено независимо и отдельно от тока.
В
постоянных магнитах магнитное поле
также вызывается движением электронов,
входящих в состав атомов и молекул
магнита.
Интенсивность
магнитного поля в каждой его точке
определяется величиной магнитной
индукции, которую принято обозначать
буквой В. Магнитная индукция является
векторной величиной, т. е. она характеризуется
не только определенным значением, но и
определенным направлением в каждой
точке магнитного поля. Направление
вектора магнитной индукции совпадает
с касательной к магнитной линии в данной
точке поля (рис. 73).
В
результате обобщения опытных данных
французские ученые Био и’Савар установили,
что магнитная индукция В (интенсивность
магнитного поля) на расстоянии г от
бесконечно длинного прямолинейного
проводника с током определяется
выражением
![]()
где
r — радиус окружности, проведенной через
рассматриваемую точку поля; центр
окружности находится на оси проводника
(2πr — длина окружности);
I
— величина тока, протекающего по
проводнику.
Величина
μа, характеризующая магнитные свойства
среды, называется а б с о л ю т н о й м а
г н и т ной проницаемостью среды.
Для
пустоты абсолютная магнитная проницаемость
имеет минимальное значение и ее принято
обозначать ц„ и называть абсолютной
магнитной проницаемостью пустоты.
![]()
Отношение
![]()
показывающее, во
Но сколько раз абсолютная магнитная
проницаемость данной среды больше
абсолютной магнитной проницаемости
пустоты, называется относительной
магнитной проницаемостью и обозначается
буквой μ.
В
Международной системе единиц (СИ) приняты
единицы измерения магнитной индукции
В — тесла или вебер на квадратный метр
(тл, вб/м2).
В
инженерной практике магнитную индукцию
принято измерять в гауссах (гс): 1 тл =
104 гс.
Если
во всех точках магнитного поля вектора
магнитной индукции равны по величине
и параллельны друг другу, то такое поле
называется однородны м.
Произведение
магнитной индукции В на величину площадки
S, перпендикулярной направлению поля
(вектору магнитной индукции), называется
потоком вектора магнитной индукции,
или просто
м
а г н и т н ы м п о т о к о м, и обозначается
буквой Ф (рис. 74): Ф=BS.

В
Международной системе в качестве единицы
измерения магнитного потока принят
вебер (вб).
В
инженерных расчетах магнитный поток
измеряют в максвеллах (мке):
1вб=108
мкс.
При
расчетах магнитных полей пользуются
также величиной, называемой
напряженностью магнитного поля
(обозначается Н). Магнитная индукция
В и напряженность магнитного поля Н
связаны соотношением
![]()
Единица
измерения напряженности магнитного
поля Н — ампер на метр (а/м).
Напряженность
магнитного поля в однородной среде, так
же как и магнитная индукция, зависит от
величины тока, числа и формы проводников,
по которым проходит ток. Но в отличие
от магнитной индукции напряженность
магнитного поля не учитывает влияния
магнитных свойств среды.
Закон
Ампера
устанавливает, что на проводник с током,
помещенный в однородное магнитное поле,
индукция которого В, действует сила,
пропорциональная силе тока и индукции
магнитного поля:
F
= BIlsina (a – угол между направлением тока
и индукцией магнитного поля ). Эта формула
закона Ампера оказывается справедливой
для прямолинейного проводника и
однородного поля.
Если
проводник имеет произвольную формулу
и поле неоднородно, то Закон Ампера
принимает вид:
dF
= I*B*dlsina
Закон
Ампера в векторной форме:
dF
= I [dl B]
Сила
Ампера направлена перпендикулярно
плоскости, в которой лежат векторы dl и
B.
Для
определения направления силы, действующей
на проводник с током, помещенный в
магнитное поле, применяется правило
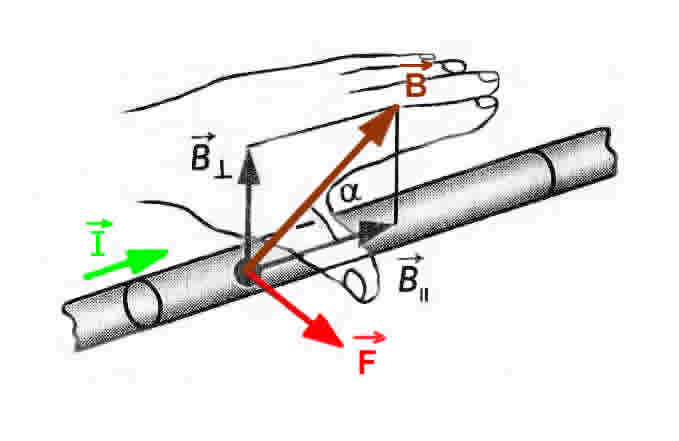
левой руки.*( Правило
левой руки Если левую руку расположить
так, чтобы линии магнитной индукции
входили в ладонь, а вытянутые четыре
пальца совпадали с направлением тока
в проводнике, то отогнутый большой палец
укажет направление силы, действующей
на проводник с током, помещенный в
магнитное поле.)
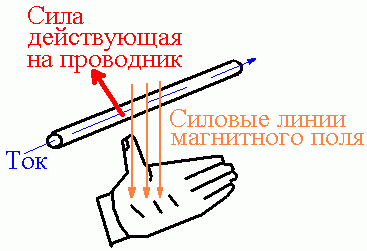
Сила
Ампера.На проводник с
током, находящийся в магнитном поле,
действует сила, равная
F
= I·L·B·sina
I
– сила тока в проводнике;
B
– модуль вектора индукции магнитного
поля;
L
– длина проводника, находящегося в
магнитном поле;
a
– угол между вектором магнитного поля
инаправлением тока в проводнике.
Силу,
действующую на проводник с током в
магнитном поле, называют силой Ампера.
Максимальная
сила Ампера равна:
F
= I·L·B
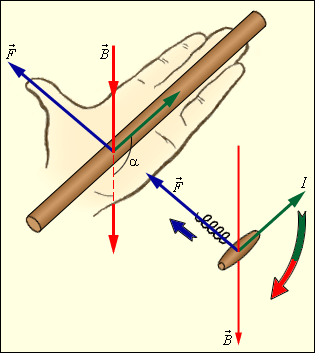
Ей
соответствует a = 90 градусов
Направление
силы Ампера определяется по правилу
левой руки: если левую руку расположить
так, чтобы перпендикулярная составляющая
вектора магнитной индукции В входила
в ладонь, а четыре вытянутых пальца были
направлены по направлению тока, то
отогнутый на 90 градусов большой палец
покажет направление силы, действующей
на отрезок проводника с током, то есть
силы Ампера.
-
Магни́тный
моме́нт, магни́тный дипо́льный моме́нт
— основная величина, характеризующая
магнитные свойства вещества. Источником
магнетизма, согласно классической
теории электромагнитных явлений,
являются электрические макро- и
микротоки. Элементарным источником
магнетизма считают замкнутый ток.
Магнитным моментом обладают элементарные
частицы, атомные ядра, электронные
оболочки атомов и молекул. Магнитный
момент элементарных частиц (электронов,
протонов, нейтронов и других), как
показала квантовая механика, обусловлен
существованием у них собственного
механического момента — спина.
Магнитный
момент измеряется в А⋅м2
или
Дж/Тл
(СИ),
либо
эрг/Гс
(СГС),
1 эрг/Гс
= 10-3 Дж/Тл.
Специфической
единицей
элементарного
магнитного
момента
является
магнетон
Бора.
В
случае плоского контура с электрическим
током магнитный момент вычисляется как
![]()
где
![]()
— сила тока в контуре,
— площадь контура,
— единичный вектор нормали к плоскости
контура. Направление магнитного момента
обычно находится по правилу буравчика:
если вращать ручку буравчика в направлении
тока, то направление магнитного момента
будет совпадать с направлением
поступательного движения буравчика.
Для
произвольного замкнутого контура
магнитный момент находится из
![]()
где
r
— радиус-вектор, проведенный из начала
координат до элемента длины контура
dl.
В
общем случае произвольного распределения
токов в среде:
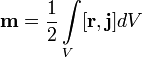
где
j
— плотность тока в элементе объёма dV
Пусть
в однородное магнитное поле помещена
рамка с током (рис. 4.13). Тогда силы Ампера,
действующие на боковые стороны рамки,
будут создавать вращающий момент,
величина которого пропорциональна
магнитной индукции, силе тока в рамке,
ее площади S и зависит от угла a между
вектором
![]()
и нормалью к площади
![]()
:
![]()
Направление
нормали выбирают так, чтобы в направлении
нормали перемещался правый винт при
вращении по направлению тока в рамке.
Максимальное
значение вращательный момент имеет
тогда, когда рамка устанавливается
перпендикулярно магнитным силовым
линиям:
![]()
.
Это
выражение также можно использовать для
определения индукции магнитного поля:
![]()
Величину,
равную произведению
![]()
, называют магнитным моментом контура
Рт. Магнитный момент есть вектор,
направление которого совпадает с
направлением нормали к контуру. Тогда
вращательный момент можно записать
![]()
При
угле a
= 0 вращательный момент равен нулю.
Значение вращательного момента зависит
от площади контура, но не зависит от его
формы. Поэтому на любой замкнутый контур,
по которому течет постоянный ток,
действует вращательный момент М, который
поворачивает его так, чтобы вектор
магнитного момента установился
параллельно вектору индукции магнитного
поля.
-
На
проводник с током в магнитном поле
действуют силы, которые определяются
с помощью закона Ампера. Если проводник
не закреплен (например, одна из сторон
контура сделана в виде подвижной
перемычки, рис. 1), то под действием силы
Ампера он в магнитном поле будет
перемещаться. Значит, магнитное поле
совершает работу по перемещению
проводника с током.
Для
вычисления этой работы рассмотрим
проводник длиной l
с током I
(он может свободно двигаться), который
помещен в однородное внешнее магнитное
поле, которое перпендикулярно плоскости
контура. Сила, направление которой
определяется по правилу левой руки, а
значение — по закону Ампера, рассчитывается
по формуле
![]()
Под
действием данной силы проводник
передвинется параллельно самому себе
на отрезок dx
из положения 1 в положение 2. Работа,
которая совершается магнитным полем,
равна
![]()
так
как ldx=dS
— площадь, которую пересекает проводник
при его перемещении в магнитном поле,
BdS=dФ
— поток вектора магнитной индукции,
который пронизывает эту площадь. Значит,
![]()
1
т.
е. работа по перемещению проводника с
током в магнитном поле равна произведению
силы тока на магнитный поток, пересеченный
движущимся проводником. Данная формула
справедлива и для произвольного
направления вектора В.
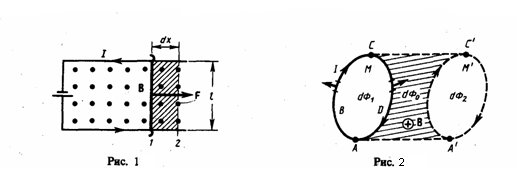
Рассчитаем
работу по перемещению замкнутого контура
с постоянным током I
в магнитном поле. Будем считать, что
контур М перемещается в плоскости
чертежа и в результате бесконечно малого
перемещения перейдет в положение М’,
изображенное на рис. 2 штриховой линией.
Направление тока в контуре (по часовой
стрелке) и магнитного поля (перпендикулярно
плоскости чертежа — за чертеж или от
нас) дано на рисунке. Контур М условно
разобьем на два соединенных своими
концами проводника: AВС
и CDА.
Работа
dA,
которая совершается силами Ампера при
иссследуемом перемещении контура в
магнитном поле, равна алгебраической
сумме работ по перемещению проводников
AВС
(dA1)
и CDA
(dA2),
т. е.
![]()
2
Силы,
которые приложенны к участку CDA
контура, образуют острые углы с
направлением перемещения, поэтому
совершаемая ими работа dA2>0.
.Используя (1), находим, эта работа равна
произведению силы тока I
в нашем контуре на пересеченный
проводником CDA
магнитный поток. Проводник CDA
пересекает при своем движении поток
dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ2,
который пронизывает контур в его конечном
положении. Значит,
![]()
3
Силы,
которые действуют на участок AВС
контура, образуют тупые углы с направлением
перемещения, значит совершаемая ими
работа dA1<0.
Проводник AВС
пересекает при своем движении поток
dФ0
сквозь поверхность, выполненную в цвете,
и поток dФ1,
который пронизывает контур в начальном
положении. Значит,
![]()
4
Подставляя
(3) и (4) в (2), найдем выражение для
элементарной работы:
![]()
де
dФ2—dФ1=dФ’
— изменение магнитного потока сквозь
площадь, которая ограничена контуром
с током. Таким образом,
![]()
5
Проинтегрировав
выражение (5), найдем работу, которая
совершается силами Ампера, при конечном
произвольном перемещении контура в
магнитном поле:
![]()
6
значит,
работа по перемещению замкнутого контура
с током в магнитном поле равна произведению
силы тока в контуре на изменение
магнитного потока, сцепленного с
контуром. Выражение (6) верно для контура
любой формы в произвольном магнитном
поле.
-
Экспериментальные
исследования показали, что все вещества
в большей или меньшей степени обладают
магнитными свойствами. Если два витка
с токами поместить в какую-либо среду,
то сила магнитного взаимодействия
между токами изменяется. Этот опыт
показывает, что индукция магнитного
поля, создаваемого электрическими
токами в веществе, отличается от индукции
магнитного поля, создаваемого теми же
токами в вакууме.
Физическая
величина, показывающая, во сколько раз
индукция
магнитного поля в
однородной среде отличается по модулю
от индукции
![]()
магнитного поля в вакууме, называется
магнитной проницаемостью:
![]()
Магнитные
свойства веществ определяются магнитными
свойствами атомов или элементарных
частиц (электронов, протонов и нейтронов),
входящих в состав атомов. В настоящее
время установлено, что магнитные свойства
протонов и нейтронов почти в 1000 раз
слабее магнитных свойств электронов.
Поэтому магнитные свойства веществ в
основном определяются электронами,
входящими в состав атомов.
Одним
из важнейших свойств электрона является
наличие у него не только электрического,
но и собственного магнитного поля.
Собственное магнитное поле электрона
называют спиновым (spin
– вращение). Электрон создает магнитное
поле также и за счет орбитального
движения вокруг ядра, которое можно
уподобить круговому микротоку. Спиновые
поля электронов и магнитные поля,
обусловленные их орбитальными движениями,
и определяют широкий спектр магнитных
свойств веществ.
Вещества
крайне разнообразны по своим магнитным
свойствам. У большинства веществ эти
свойства выражены слабо. Слабо-магнитные
вещества делятся на две большие группы
– парамагнетики и диамагнетики. Они
отличаются тем, что при внесении во
внешнее магнитное поле парамагнитные
образцы намагничиваются так, что их
собственное магнитное поле оказывается
направленным по внешнему полю, а
диамагнитные образцы намагничиваются
против внешнего поля. Поэтому у
парамагнетиков μ
> 1, а у диамагнетиков μ
< 1. Отличие μ
от единицы у пара- и диамагнетиков
чрезвычайно мало. Например, у алюминия,
который относится к парамагнетикам, μ
– 1 ≈ 2,1·10–5, у хлористого железа (FeCl3)
μ
– 1 ≈ 2,5·10–3. К парамагнетикам относятся
также платина, воздух и многие другие
вещества. К диамагнетикам относятся
медь (μ
– 1 ≈ –3·10–6), вода (μ
– 1 ≈ –9·10–6), висмут (μ
– 1 ≈ –1,7·10–3) и другие вещества. Образцы
из пара- и диамагнетика, помещенные в
неоднородное магнитное поле между
полюсами электромагнита, ведут себя
по-разному – парамагнетики втягиваются
в область сильного поля, диамагнетики
– выталкиваются (рис. 1.19.1).
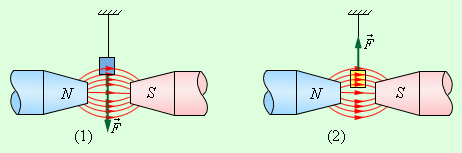
Парамагнетик
(1) и диамагнетик (2) в неоднородном
магнитном поле.
Пара-
и диамагнетизм объясняется поведением
электронных орбит во внешнем магнитном
поле. У атомов диамагнитных веществ в
отсутствие внешнего поля собственные
магнитные поля электронов и поля,
создаваемые их орбитальным движением,
полностью скомпенсированы. Возникновение
диамагнетизма связано с действием силы
Лоренца на электронные орбиты. Под
действием этой силы изменяется характер
орбитального движения электронов и
нарушается компенсация магнитных полей.
Возникающее при этом собственное
магнитное поле атома оказывается
направленным против направления индукции
внешнего поля.
В
атомах парамагнитных веществ магнитные
поля электронов скомпенсированы не
полностью, и атом оказывается подобным
маленькому круговому току. В отсутствие
внешнего поля эти круговые микротоки
ориентированы произвольно, так что
суммарная магнитная индукция равна
нулю. Внешнее магнитное поле оказывает
ориентирующее действие – микротоки
стремятся сориентироваться так, чтобы
их собственные магнитные поля оказались
направленными по направлению индукции
внешнего поля. Из-за теплового движения
атомов ориентация микротоков никогда
не бывает полной. При усилении внешнего
поля ориентационный эффект возрастает,
так что индукция собственного магнитного
поля парамагнитного образца растет
прямо пропорционально индукции внешнего
магнитного поля. Полная индукция
магнитного поля в образце складывается
из индукции внешнего магнитного поля
и индукции собственного магнитного
поля, возникшего в процессе намагничивания.
Механизм намагничивания парамагнетиков
очень похож на механизм поляризации
полярных диэлектриков. Диамагнетизм
не имеет аналога среди электрических
свойств вещества.
Следует
отметить, что диамагнитными свойствами
обладают атомы любых веществ. Однако
во многих случаях диамагнетизм атомов
маскируется более сильным парамагнитным
эффектом. Явление диамагнетизма было
открыто М. Фарадеем в 1845 г.
Вещества,
способные сильно намагничиваться в
магнитном поле, называются ферромагнетиками.
Магнитная проницаемость ферромагнетиков
по порядку величины лежит в пределах
102–105. Например, у стали μ
≈ 8000, у сплава железа с никелем магнитная
проницаемость достигает значений
250000.
К
рассматриваемой группе относятся четыре
химических элемента: железо, никель,
кобальт, гадолиний. Из них наибольшей
магнитной проницаемостью обладает
железо. Поэтому вся эта группа получила
название ферромагнетиков.
Ферромагнетиками
могут быть различные сплавы, содержащие
ферромагнитные элементы. Широкое
применение в технике получили керамические
ферромагнитные материалы – ферриты.
Для
каждого ферромагнетика существует
определенная температура (так называемая
температура или точка Кюри), выше которой
ферромагнитные свойства исчезают, и
вещество становится парамагнетиком. У
железа, например, температура Кюри равна
770 °C,
у кобальта 1130 °C,
у никеля 360 °C.
Ферромагнитные
материалы делятся на две большие группы
– на магнито-мягкие и магнито-жесткие
материалы. Магнито-мягкие ферромагнитные
материалы почти полностью размагничиваются,
когда внешнее магнитное поле становится
равным нулю. К магнито-мягким материалам
относится, например, чистое железо,
электротехническая сталь и некоторые
сплавы. Эти материалы применяются в
приборах переменного тока, в которых
происходит непрерывное перемагничивание,
то есть изменение направления магнитного
поля (трансформаторы, электродвигатели
и т. п.).
Магнито-жесткие
материалы в значительной мере сохраняют
свою намагниченность и после удаления
их из магнитного поля. Примерами
магнито-жестких материалов могут служить
углеродистая сталь и ряд специальных
сплавов. Магнито-жесткие метериалы
используются в основном для изготовления
постоянных магнитов.
Магнитная
проницаемость μ
ферромагнетиков не является постоянной
величиной; она сильно зависит от индукции
B0
внешнего поля. Типичная зависимость μ
(B0)
приведена на рис. 1.19.2. В таблицах обычно
приводятся значения максимальной
магнитной проницаемости.
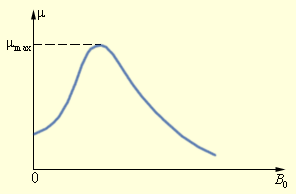
Типичная
зависимость магнитной проницаемости
ферромагнетика от индукции внешнего
магнитного поля
Непостоянство
магнитной проницаемости приводит к
сложной нелинейной зависимости индукции
B
магнитного поля в ферромагнетике от
индукции B0
внешнего магнитного поля. Характерной
особенностью процесса намагничивания
ферромагнетиков является так называетмый
гистерезис, то есть зависимость
намагничивания от предыстории образца.
Кривая намагничивания B
(B0)
ферромагнитного образца представляет
собой петлю сложной формы, которая
называется петлей гистерезиса (рис.
1.19.3).
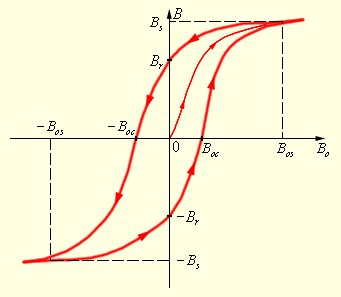
Петля
гистерезиса ферромагнетика. Стрелками
указано направление процессов
намагничивания и размагничивания
ферромагнитного образца при изменении
индукции B0
внешнего магнитного поля.
Из
рис. 1.19.3 видно, что при наступает
магнитное насыщение – намагниченность
образца достигает максимального
значения.
Если
теперь уменьшать магнитную индукцию
B0 внешнего поля и довести ее вновь до
нулевого значения, то ферромагнетик
сохранит остаточную намагниченность
– поле внутри образца будет равно Br.
Остаточная намагниченность образцов
позволяет создавать постоянные магниты.
Для того, чтобы полностью размагнитить
образец, необходимо, изменив знак
внешнего поля, довести магнитную индукцию
B0 до значения –B0c, которое принято
называть коэрцитивной силой. Далее
процесс перемагничивания может быть
продолжен, как это указано стрелками
на рис. 1.19.3.
У
магнито-мягких материалов значения
коэрцитивной силы B0c невелико – петля
гистерезиса таких материалов достаточно
узкая. Материалы с большим значением
коэрцитивной силы, то есть имеющие
широкую петлю гистерезиса, относятся
к магнито-жестким.
Природа
ферромагнетизма может быть до конца
понята только на основе квантовых
представлений. Качественно ферромагнетизм
объясняется наличием собственных
(спиновых) магнитных полей у электронов.
В кристаллах ферромагнитных материалов
возникают условия, при которых, вследствие
сильного взаимодействия спиновых
магнитных полей соседних электронов,
энергетически выгодной становится их
параллельная ориентация. В результате
такого взаимодействия внутри кристалла
ферромагнетика возникают самопроизвольно
намагниченные области размером порядка
10–2–10–4 см. Эти области называются
доменами. Каждый домен представляет из
себя небольшой постоянный магнит.
В
отсутствие внешнего магнитного поля
направления векторов индукции магнитных
полей в различных доменах ориентированы
в большом кристалле хаотически. Такой
кристалл в среднем оказывается
ненамагниченным. При наложении внешнего
магнитного поля происходит смещение
границ доменов так, что объем доменов,
ориентированных по внешнему полю,
увеличивается. С увеличением индукции
внешнего поля возрастает магнитная
индукция намагниченного вещества. В
очень сильном внешнем поле домены, в
которых собственное магнитное поле
совпадает по направлению с внешним
полем, поглощают все остальные домены,
и наступает магнитное насыщение. Рис.
1.19.4 может служить качественной
иллюстрацией процесса намагничивания
ферромагнитного образца.
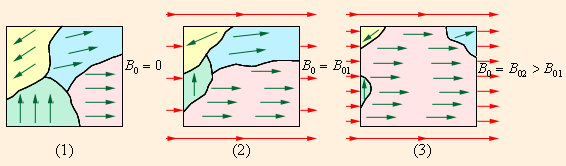
Рисунок
1.19.4.
Намагничивание
ферромагнитного образца. (1) B0
= 0; (2) B0
= B01;
(3) B0
= B02
> B01.
-
Напряженность
магнитного
поля необходима для определения
магнитной индукции поля, создаваемого
токами различной конфигурации в
различных средах. Напряженность
магнитного поля характеризует магнитное
поле в вакууме.
Напряженность
магнитного поля (формула) векторная
физическая величина, равная:
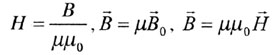
Напряженность
магнитного поля в СИ – ампер на метр
(А/м).
Векторы
индукции (В) и напряженности магнитного
поля (Н) совпадают по направлению. Если
знать Напряженность магнитного поля в
данной точке, то можно определить
индукцию поля в этой точке.
Напряженность
магнитного поля зависит только от силы
тока, протекающего по проводнику, и его
геометрии.
Закон
полного тока
это закон, связывающий циркуляцию
вектора напряженности магнитного поля
и ток.
Циркуляция
вектора напряженности магнитного поля
по контуру равна алгебраической сумме
токов, охватываемых этим контуром.
![]()
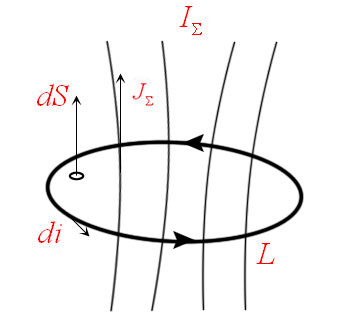
Положительным
считается ток, направление которого
связано с направлением обхода по контуру
правилом правого винта; ток протоивоположного
направления считается отрицательным.
![]()
-
Основные
хар-ки диа-пара-ферромагнетиков.
Диа-
и парамагнетики
Все
вещества обладают определенными
магнитными свойствами, т. е.
являются магнетиками.
Для большинства веществ магнитная
проницаемость μ близка к единице и не
зависит от величины магнитного поля.
Вещества, для которых магнитная
проницаемость незначительно меньше
единицы (μ < 1), называются диамагнетиками,
незначительно больше единицы (μ > 1)
—парамагнетиками.
Вещества, магнитная проницаемость
которых зависит от величины внешнего
поля и может значительно превышать
единицу (μ » 1), называются ферромагнетиками.
В диамагнетиках молекулы
не обладают собственным магнитным
полем. Под действием внешнего магнитного
поля в атомах и молекулах поле токов
намагниченности направлено противоположно
внешнему полю, поэтому модуль вектора
магнитной индукции ![]()
результирующего
поля будет меньше модуль вектора
магнитной индукции ![]()
внешнего
поля.
В парамагнетиках молекулы
обладают собственным магнитным полем.
В отсутствии внешнего магнитного поля
из-за теплового движения вектора индукций
магнитных полей атомов и молекул
ориентированы хаотически, поэтому их
средняя намагниченность равна нулю.
При наложении внешнего магнитного поля
на атомы и молекулы начинает действовать
момент сил, стремящийся повернуть их
так, чтобы их поля были ориентированы
параллельно внешнему полю. Ориентация
молекул парамагнетика приводит к тому,
что вещество намагничивается. Полной
ориентации молекул в магнитном поле
препятствует их тепловое движение,
поэтому магнитная проницаемость
парамагнетиков зависит от температуры.
Главная
особенность ферромагнетиков заключается
в способности сохранять намагниченность
в отсутствии внешнего магнитного поля,
все постоянные магниты относятся к
классу ферромагнетикам.
Свойства
ферромагнетиков
1)
ферромагнитные свойства вещества
проявляются только тогда, когда
соответствующее вещество находится в
кристаллическом состоянии;
2)
магнитные свойства ферромагнетиков
сильно зависят от температуры, так как
ориентации магнитных полей доменов
препятствует тепловое движение. Для
каждого ферромагнетика существует
определенная температура, при котором
доменная структура полностью разрушается,
и ферромагнетик превращается в
парамагнетик. Это значение температуры
называется точкой
Кюри.
Так для чистого железа значение
температуры Кюри приблизительно равно
900°C;
3)
ферромагнетики намагничиваются до
насыщения в
слабых магнитных полях.
-
Явление
электромагнитной индукции. Опыт Фарадея.
Правило Ленца.
Явление,
заключающееся в том, что в замкнутом
проводящем контуре при изменении потока
магнитной индукции, охватываемого этим
контуром, возникает электрический ток,
получивший название индукционного.
Опыт1
Фарадея. Если в замкнутый на гальванометр
соленоид вдвигать или выдвигать
постоянный магнит, то в моменты его
вдвигания или выдвигания наблюдается
отклонение стрелки тем больше, чем
быстрее движется магнит относительно
катушки. При изменении полюсов магнита
направление отклонения стрелки изменится.
Опыт2.
Концы одной из катушек, вставленных
одна в другую, присоединяются к
гальванометру, а через другую пропускается
ток. Отклонение стрелки гальванометра
наблюдается в моменты включения или
выключения тока, в моменты его увеличения
или уменьшения или при перемещении
катушек друг относительно друга.
Выводы:
Индукционный ток возникает всегда,
когда происходит изменение сцепленного
с контуром потока магнитной индукции.
Сила индукционного тока совершенно не
зависит от способа изменения потока
магнитной индукции, а определяется лишь
скоростью его изменения.
Правило
Ленца. Фарадей
экспериментально
установил, что при изменении магнитного
потока в проводящем контуре возникает
ЭДС индукции ![]()
инд,
равная скорости изменения магнитного
потока через поверхность, ограниченную
контуром, взятой со знаком минус:
|
|
Формула
показывает, что увеличение потока
вызывает
инд<0
, уменьшение потока вызывает
инд>0.
Индукционный ток в контуре имеет всегда
такое направление, что создаваемое им
магнитное поле препятствует изменению
магнитного потока, вызвавшему этот
индукционный ток.
-
Закон
электромагнитной индукции (вывод).
Всякий
раз, когда происходит изменение
сцепленного с контуром потока магнитной
индукции, в контуре возникает индукционный
ток, что и указывает на наличие в цепи
ЭДС, называемой ЭДС электромагнитной
индукции.

– закон
электромагнитной индукции,который
может быть непосредственно получен из
закона сохранения энергии, как это
впервые сделал Г. Гельмгольц. Рассмотрим
проводник с током I,
который помещен в однородное магнитное
поле, перпендикулярное плоскости
контура, и может свободно перемещаться.
Под действием силы Ампера F,
проводник перемещается на отрезок dx.
Таким образом, сила Ампера производит
работу dA=IdФ,
где dФ
— пересеченный проводником магнитный
поток.
Согласно
закону сохранения энергии, работа
источника тока за время dt
(![]()
)
будет складываться из работы на джоулеву
теплоту (I2Rdt)
и работы по перемещению проводника в
магнитном поле (IdФ):
![]()
где
R
— полное
сопротивление контура. Тогда
![]()

=
![]()
есть не что иное, как закон Фарадея
-
Токи
Фуко. ЭДС самоиндукции, индуктивность
соленоида.
Индукционный
ток возникает и в массивных сплошных
проводниках, помещённых в переменное
магнитное поле. Эти токи замкнуты в
толще проводника и называются вихревыми
токами(токами Фуко). Токи Фуко также
подчиняются правилу Ленца: их магнитное
поле направлено так, чтобы противодействовать
изменению магнитного потока, индуцирующего
вихревые токи.
1.Использование
токов – индукционный нагрев.
2.Происходит
вытеснение тока высокой частоты на
поверхность проводников.
3.Токи
Фуко вызывают нежелательный нагрев,
поэтому возможен разрыв по сечению.
Самоиндукция
– возникновение ЭДС индукции в проводящем
контуре при изменении в нем силы тока.
Применяя к самоиндукции закон Фарадея,
запишем:
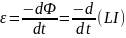
Если
контур не деформируется и магнитная
проницаемость среды не изменяется, то
L=const
и

, где знак минус, обусловленный правилом
Ленца, показывает, что наличие индуктивности
в контуре приводит к замедлению изменения
тока в нем.
Индуктивность
соленоида. Пусть
число витков соленоида – N, площадь
поперечного сечения витка – S,
длина
соленоида – l, а
полость соленоида заполнена средой с
относительной магнитной проницаемостью
µ. При протекании по обмотке соленоида
тока I
внутри
соленоида возникает однородное поле,
индукция которого
B=µµ0nI
(3.14),
где n= N/l – число
витков на единицу длины катушки. Магнитный
поток через каждый из витков равен ВS, а
через все витки
Ф
= NBS
= nlBS
(3.15)
Подставляя
значение В из
(3.14) получим:
![]()
(3.16)
Далее
имеем
![]()
(3.17)
где V = lS – объем соленоида.
-
Энергия
магнитного поля, объёмная плотность
энергии.
Магнитное
поле обладает энергией. Если включить
электрическую лампу параллельно катушке
с большой индуктивностью в электрическую
цепь постоянного тока, то при размыкании
ключа наблюдается кратковременная
вспышка лампы. Ток в цепи возникает под
действием ЭДС самоиндукции. Источником
энергии, выделяющейся при этом в
электрической цепи, является магнитное
поле катушки.
Энергия Wм магнитного
поля катушки с индуктивностью L,
создаваемого током I,
равна
|
Эта
энергия может быть получена от ЭДС при
включении цепи.
Магнитная
энергия локализована не в витках катушки,
по которым протекает ток, а рассредоточена
по всему объему, в котором создано
магнитное поле. Физическая величина
|
равная
энергии магнитного поля в единице
объема, называется объемной
плотностью магнитной энергии.
Максвелл показал, что выражение для
объемной плотности магнитной энергии,
выведенное здесь для случая длинного
соленоида, справедливо для любых
магнитных полей.
-
Вихревое
магнитное поле. Уравнение Максвелла.
По
Максвеллу, изменяющееся по времени
магнитное поле порождает электрическое
поле E,
циркуляция которого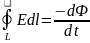
Если
поверхность и контур неподвижны, то

Таким
образом, циркуляция вектора Е не равна
нулю, т. е.
электрическое поле Е, возбуждаемое
переменным магнитным полем, как и само
магнитное поле, является вихревым.
Рассмотрим
случай для неподвижного контура,
помещённого в изменяемое магнитное
поле, в таком контуре возникает ЭДС
индукции и возникает индукционный ток.
Уравнение
Максвелла в интегральной форме:
Уравнение
в дифференциальной форме:

-
Основы
релятивистской механики. Преобразования
Лоренца.
Релятивистская
механика —
раздел физики,
рассматривающий законы механики
при скоростях, сравнимых со скоростью
света.
Релятивистская механика — теория,
в которой, в отличие от классической
механики, где пространственные координаты
и время являются независимыми, при
отсутствии голономных связей зависящих
от времени, (время является абсолютным,
то есть течёт одинаково во всех системах
отсчёта) и действуют преобразования
Галилея, события происходят в четырёхмерном
пространстве, объединяющем физическое
трёхмерное пространство и время и
действуют преобразования
Лоренца. Таким образом, в отличие от
классической механики, одновременность
событий зависит от выбора системы
отсчёта.
Основные
законы релятивистской механики —
релятивистское обобщение второго закона
Ньютона и релятивистский закон сохранения
энергии-импульса являются следствием
такого «смешения» пространственных и
временной координат при преобразованиях
Лоренца.
Пусть
координатные оси двух инерциальных
систем отсчёта S и S’ параллельны друг
другу, (t, x,y, z) — время и координаты
некоторого события,
наблюдаемого относительно системы S, а
(t’,x’,y’,z’) — время и координаты того
же события
относительно системы S’. Если система
S’ движется равномерно и прямолинейно
со скоростью v относительно S, то
справедливы преобразования Лоренца:
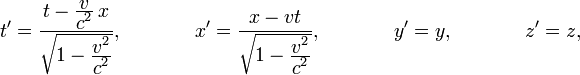
где ![]()
-скорость
света. При скоростях много меньше
скорости света (![]()
)
преобразования Лоренца переходят
в преобразования
Галилея:
![]()
Подобный
предельный переход является
отражением принципа
соответствия, согласно которому более
общая теория (СТО) имеет своим предельным
случаем менее общую теорию (в данном
случае — классическую
механику).
Преобразования
Лоренца можно записать в векторном
виде [24],
когда скорость систем отсчёта направлена
в произвольном направлении (не обязательно
вдоль оси ![]()
):
![]()
где ![]()
—
фактор Лоренца, ![]()
и ![]()
—
радиус-векторы события относительно
систем S и S’.
-
Следствия
из СТО. Релятивистское уравнение
динамики.
Следствия:
1.
Одновременность событий в разных
системах отсчета.
Пусть в системе К
в точках с координатами x1
и x2
в моменты времени t1
и t2
происходят два события. В системе К’
им соответствуют
координаты
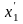
и
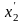
и моменты времени
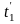
и

.
Если события
в системе К происходят в одной точке
(x1
=х2)
и
являются одновременными (t1
=t2),
то, согласно преобразованиям Лоренца
(36.3),
![]()
т.
е. эти события
являются одновременными и пространственно
совпадающими для любой инерциальной
системы отсчета.
Если
события в
системе К пространственно разобщены
(х1
x2),
но одновременны
(t1
= t2),
то в системе
К’, согласно
преобразованиям Лоренца (36.3),
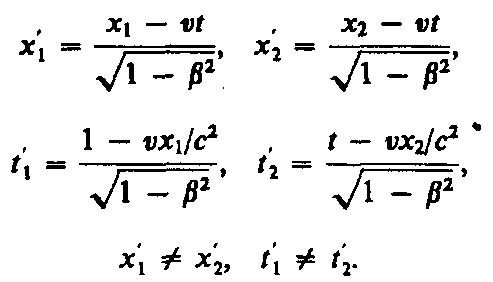
2.
Длительность событий в разных системах
отсчета.
Пусть в некоторой точке (с координатой
х),
покоящейся относительно системы К,
происходит событие, длительность
которого (разность показаний часов в
конце и начале события)
= t2
– t1,
где индексы 1 и 2 соответствуют началу
и концу события. Длительность этого же
события в системе К’
![]()
(37.1)
причем
началу и концу события, согласно (36.3),
соответствуют
![]()
(37.2)
Подставляя
(37.2) в (37.1), получаем
![]()
или
![]()
(37.3)
Из
соотношения (37.3) вытекает, что <‘,
т. е. длительность
события, происходящего в некоторой
точке, наименьшая в той инерциальной
системе отсчета, относительно которой
эта точка неподвижна.
Этот результат может быть еще истолкован
следующим образом: интервал времени
‘,
отсчитанный по часам в системе К’,
с точки зрения
наблюдателя в системе К,
продолжительнее интервала ,
отсчитанного по его часам. Следовательно,
часы, движущиеся
относительно инерциальной системы
отсчета, идут медленнее покоящихся
часов, т. е.
ход часов замедляется в системе отсчета,
относительно которой часы движутся. На
основании относительности понятий
«неподвижная» и «движущаяся» системы
соотношения для
и ‘
обратимы. Из (37.3) следует, что замедление
хода часов становится заметным лишь
при скоростях, близких к скорости
распространения света в вакууме.
3.
Длина тел
в разных
системах
отсчета.
Рассмотрим стержень, расположенный
вдоль оси х’
и покоящийся относительно системы К’.
Длина стержня в системе К’
будет
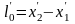
,
где
и
—
не изменяющиеся со временем t‘
координаты начала и конца стержня, а
индекс 0 показывает, что в системе отсчета
К’
стержень покоится. Определим длину
этого стержня в системе К,
относительно которой он движется со
скоростью v.
Для этого необходимо измерить координаты
его концов x1
и x2
в системе
К в один и тот
же момент времени t.
Их разность l
= х2
– х1
и определяет длину стержня в системе
К.
Используя преобразования Лоренца
(36.3), получим
![]()
т.
е.
![]()
(37.4)
Таким
образом, длина стержня, измеренная в
системе, относительно которой он
движется, оказывается меньше длины,
измеренной в системе, относительно
которой стержень покоится. Если стержень
покоится в системе К,
то, определяя его длину в системе К’,
опять-таки придем к выражению (37.4).
4.
Релятивистский закон сложения скоростей.
Рассмотрим движение материальной точки
в системе К’,
в свою очередь движущейся относительно
системы К со
скоростью v.
Определим скорость этой же точки в
системе К.
Если в системе К
движение точки в каждый момент времени
t
определяется координатами х,
у, z,
а в системе
К’ в
момент времени t‘
— координатами х’,
у’, z‘,
то
![]()
представляют
собой соответственно проекции на оси
х, у, z
и х’, у’, z’
вектора скорости рассматриваемой точки
относительно систем К
и К’. Согласно
преобразованиям Лоренца (36.3),
![]()
Если
материальная точка движется параллельно
оси х,
то скорость и
относительно системы К
совпадает с ux,
а скорость и’
относительно К’
— с
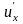
.
Тогда закон сложения скоростей примет
вид
![]()
Релятивистский
импульс:
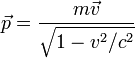
(1).
Релятивистский
импульс замкнутой системы сохраняется,
т. е. не изменяется с течением времени
– это есть следствие однородности
пространства.
Из
принципа относительности Эйнштейна,
утверждающего инвариантность всех
законов природы при переходе от одной
инерциальной системы отсчёта к другой,
следует условие инвариантности уравнений
физических законов относительно
преобразований Лоренца.
релятивистское
уравнение движения:

,
где β2
– v2/c2