Добрый день, уважаемые гости!
Сегодня, я хотел бы описать полезный совет, как очень быстро построить или измерить любой угол с помощью обычного строительного угольника, когда других инструментов попросту нет под рукой.
Нам сейчас совершенно не потребуются ни угломеры, ни транспортиры и построение угла будет произведено угольником всего лишь в три шага.
1. Построение
Шаг №1
Как мы знаем, угол — это место на плоскости между двумя пересекающимися линиями (или сторонами какого-либо предмета), которые выходят из одной точки, называемой вершиной угла.
Итак, при построении угла, ставим угольник делением “0” (ноль) см. в вершину будущего угла и от этой точки проводим прямую в нужном вам направлении, от которой необходимо построить угол (эта прямая может являться одной из граней или сторон детали, заготовки или фигуры).
После чего, на этой прямой откладываем 10 см и ставим точку (штрих).
Отметив 10 см, из этой точки проводим к прямой перпендикуляр:
Шаг №2
Для примера, мне нужно построить угол 26°! В вашем же случае он может быть любым: 13°, 25°, 49°, 74° и пр.
Берем смартфон, заходим в приложение “калькулятор”, переводим его в инженерный режим и вводим нужный вам угол. Я ввел “26″.
Далее, нажимаем кнопку “tan” или “tg”, которая обозначает “вычислить тангенс угла”.
Машина мне вывела число 0,487. Из школы мы знаем, что тангенс угла — это отношение противолежащего нашему углу катета к прилежащему. И, зная один катет 10 см и отношение катетов 0,487, мы за одну секунду вычисляем второй катет, который равен 4,87 см.
Скорее, вы теперь поняли, для чего я взял первый катет именно 10 единиц.
Для простоты вычислений! На 10 проще всего умножать, переставив запятую на один разряд вправо.
Шаг №3
Я округляю 4,87 до десятых и на перпендикуляре отмечаю 4,9 см.
Чертим гипотенузу и получаем искомый угол!
Я решил перепроверить построенный угол и приложил угольник Свенсона:
Всё верно! Получил 26°.
2. Измерение
Сейчас мы построили угол, а при измерении угла — производим все то же самое, только в обратном порядке. Измеряя угол, мы будем знать оба катета, а соответственно и их отношение. Вводим в калькуляторе значение отношения противолежащего катета к прилежащему и нажимаем кнопку “arctg”, “atg” или “tan -1”, которая обозначает обратную тангенсу функцию — арктангенс.
На дисплее калькулятора мы увидим значение нашего угла!
…написано много, а на деле все занимает не более одной минуты…
Спасибо за внимание!
starik12 Вы вообще умеете пользоваться таблицами Брадиса? Судя по тому, что вам втолковывают уже несколько дней вы первый раз о них слышали. А зря, дюже полезная книжечка.
1. Берём формулу расчёта которую вам уже дали в 5 или 9 сообщении.
2. Считаем и получаем данные, что tg@= 0.125
3 Берём в руки таблицу Брадиса и смотрим на страницу Тангенсы.
4 Ближайшие к вашим данным это цифры 0.1246 и 0.1263 стоящие в строке напротив левого вертикального столбца где написан угол 7 градусов, записываем его.
Далее высчитываем минуты.
5. До вашего значения 0.1250 первому числу в пункте 4 не хватает 0.0004, а второе больше на 0.0013.
Смотрим на крайние правые колонки. Напротив вашей строки видим цифры 3 6 9. Это поправки на которые надо надбавить или убавить данные таблицы, что бы они совпадали с вашим числом (0.1250) и обозначают они четвёртую цифру после запятой. Наиболее подходит поправка 3 как наиболее близкая к числу 0.1246.
6. Смотрим вертикально вверх от числа 0.1246, видим цифру 6. Это ваши минуты. Запимываем. Далее воспользуемся поправкой 3 про которую я писал в 4 пункте. Смотрим вверх от нее и видим цифру 1. Это число надо прибавить к вашим минутам. Получаем 6+1=7минут. Записываем к вашим градусам.
7. Далее высчитываем секунды. До ваших данных 0.1250 даже с учётом поправок не хватает 0.0001.
Смотрим на поправки. Поправка 4 составляют 1/3 часть между поправками 3 и 6. Смотрим вверх. Там поправка 3 означает 1 минуту, а поправка 6 означает 2 минуты значит поправка 4 означает на 1/3 больше 1минуты, что в конечном итоге составляет 20 секунд.
8. А вот теперь смотрим на бумажку и пишем данные полученные в пунктах 4, 6, и 7. Получаем, что данный ваш угол равен 7 градусов 7 минут 20 секунд.
Потом после того как вы выставите можно проверить способом который предложил Alex_IZA. Я так всегда делаю. Пару тончайших рисок на цилиндрической поверхности и часиками можно спокойно проверить.
Ужас, писал 15 минут, хотя считается это дело в течение 10 -15 секунд.
Углы – это геометрические фигуры, образованные двумя лучами, которые выходят из одной точки. Обозначения углов регламентированы ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений».
Как обозначается угол на чертеже
Угол на чертеже обозначается с помощью универсального и общепринятого символа, на котором показаны два луча, выходящие из одной точки. За символом указывается размер угла в градусах, минутах и секундах. Острый угол символа направлен в сторону уклона.
Обозначение углов на чертеже по ГОСТу
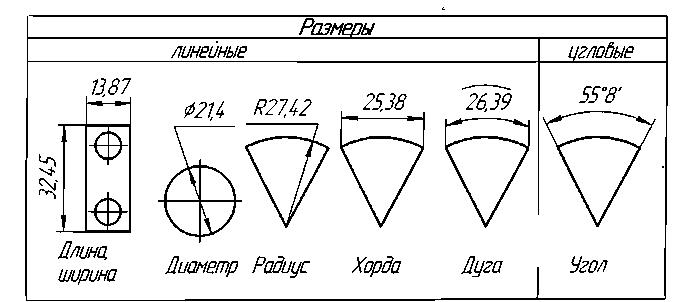
Согласно ГОСТ 2.307 размеры делятся на линейные и угловые. И если в линейных размерах не ставят единицы измерения, т. к. всегда подразумевается, что значения приведены в миллиметрах, то для угловых размеров обязательно указывается значок градуса, минуты и секунды, в зависимости от того, в каких величинах измеряется угол.
Рисунок 1. Линейные и угловые размеры
Как показать угол на чертеже
Чтобы показать размер используются сплошные тонкие линии, они могут быть выносные или размерные. Любой угол имеет вершину и две стороны. Градусами или минутами обычно обозначается внутренняя сторона угла. В качестве условного обозначения используется символ в виде острого угла, далее указывается числовое значение и единицы измерения. Следует помнить о том, что минута — это одна шестидесятая часть градуса, а секунда одна шестидесятая часть минуты. Градусы обозначаются с помощью маленького круга в верхнем правом углу возле значения, минуты обозначаются одной надстрочной запятой, а секунды двумя надстрочными запятыми.
Допуск угла
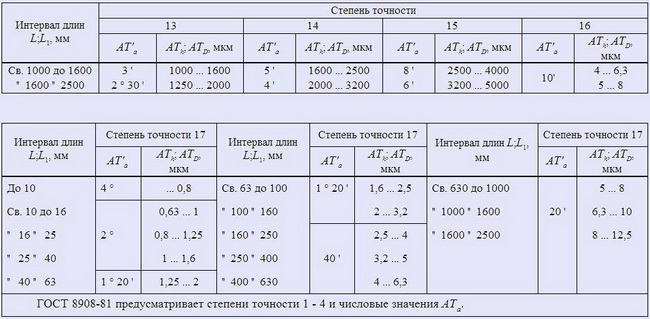
В ГОСТ 8908-81 приведены стандарты на допуски углов, применяемые в машиностроении, при меньшей стороне угла до 2,5 м. Значения уклона и угла уклона приведены в таблице (рис. 1). Стандартом установлено 17 степеней точности допусков, которые зависят от длин сторон и размера угла.
Рисунок 2. Степень точности допуска угла
Виды углов на чертеже
На чертежах могут быть обозначены следующие виды углов:
- острый – менее 90 градусов;
- прямой – равен 90 градусам;
- тупой – более 90 и менее 180 градусов;
- развернутый – равен 180 градусам.
Обозначение у прямого и развернутого угла ставится при необходимости.
Углы наклона
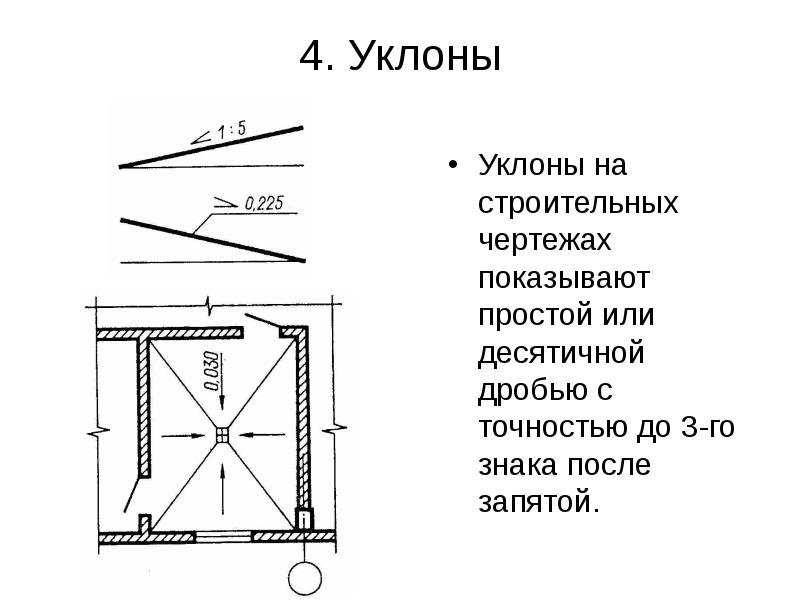
Угол уклона часто встречается как на машиностроительных, так и на строительных чертежах. Он показывает, под каким углом к базовой линии расположен наклонный элемент. Для обозначения наклона используется универсальный символ, который ставится перед размерным числом. К примеру, на строительном чертеже отмостка всегда имеет уклон, для обозначения этого уклона ставится символ и значение в 5 промилле.
Рисунок 3. Обозначение уклона на плане кровли
Промилле — это одна тысячная или десятая часть процента, поэтому к знаку промилле добавлен еще один нолик. Через промилле в строительных чертежах указывается уклон пандусов и других наклонных поверхностей.
Рисунок 4. Уклон на чертеже
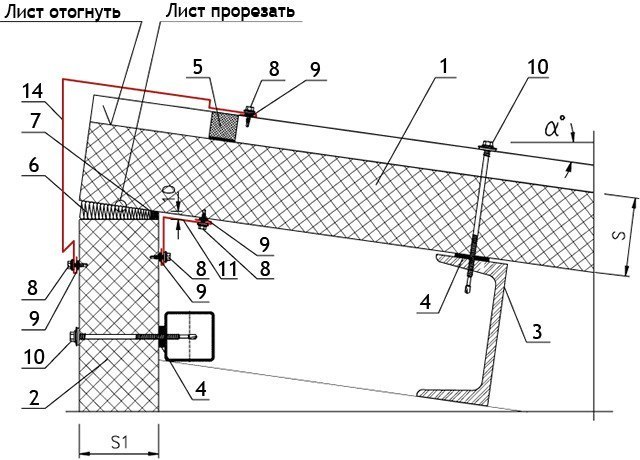
Рисунок 5. На узле сопряжения сендвич панелей указывается угол под которым конструкции крпятся друг к другу
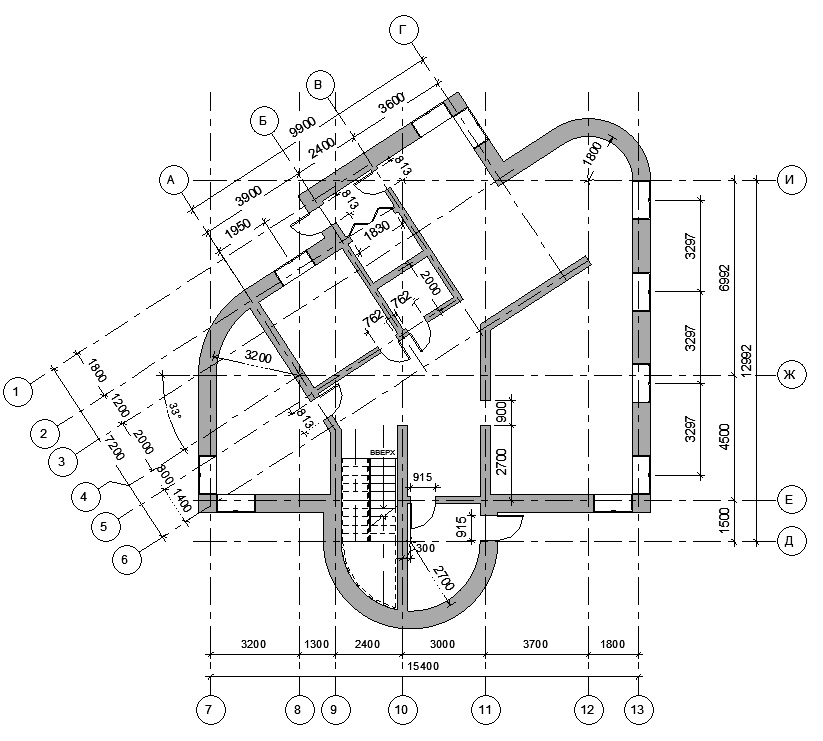
Рисунок 6. Углы. На строительном чертеже обозначен угол в 33 градуса
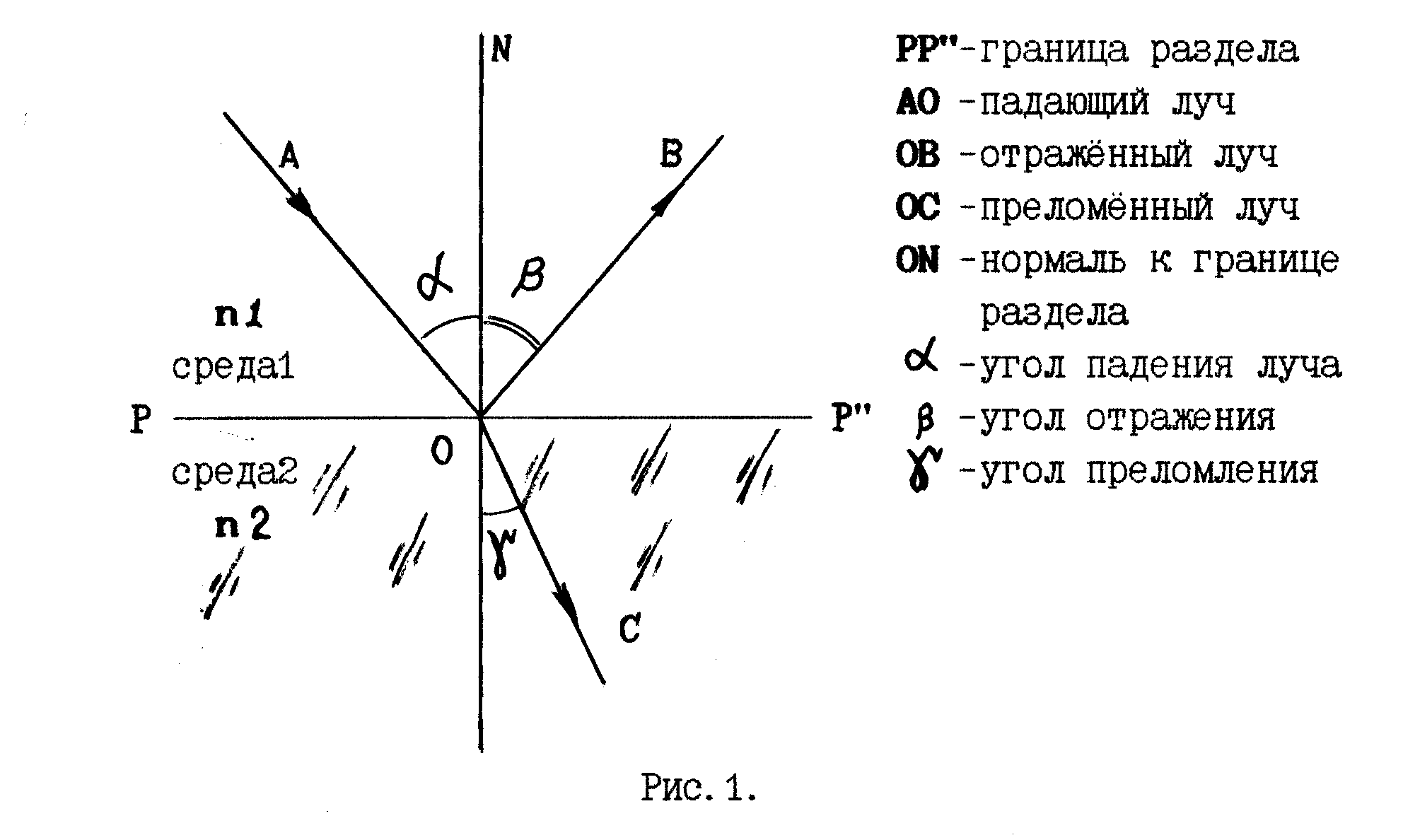
Угол преломления
Преломление возникает на границе двух сред, при этом угол падения равен углу отражения. Падающий и отраженный лучи показывают на чертеже, а значение угла наносят относительно вертикали, прямого угла.
Рисунок 7. Угол преломления
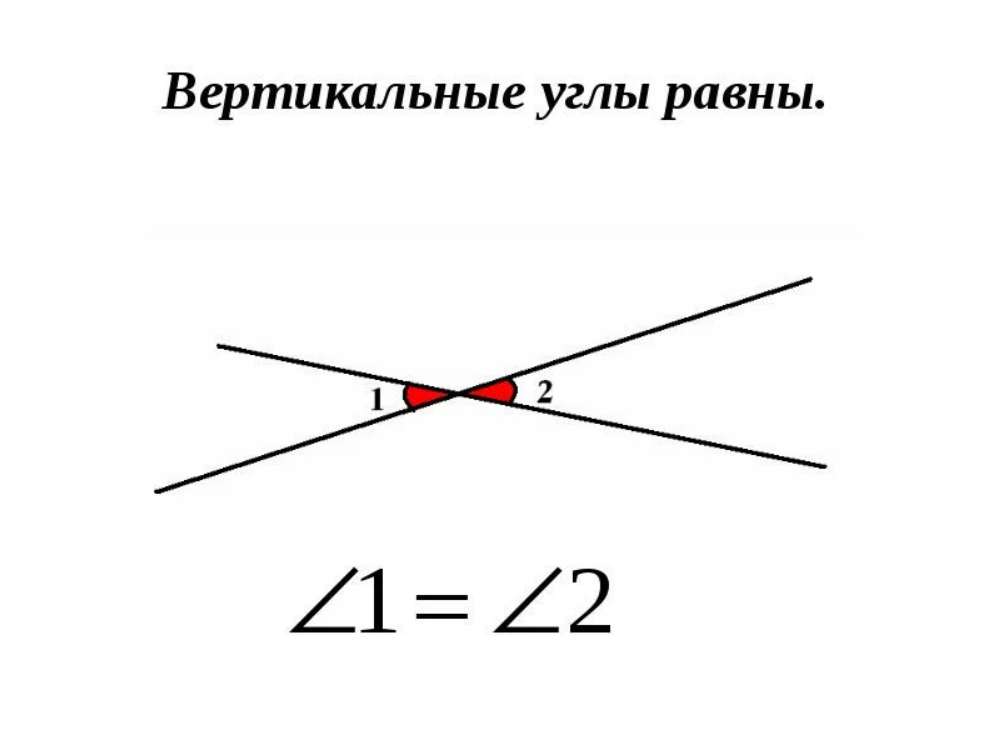
Вертикальные углы
Согласно определению вертикальными называют два угла, в том случае, если стороны одного угла являются продолжением сторон другого. Такие углы будут попарно равны. Обычно на чертеже их обозначают с помощью полукруга или двойного полукруга.
Рисунок 8. Вертикальные углы, пример обозначения
Многогранные углы
Понятие многогранного угла относится к трехмерному пространству, такой угол состоит из плоских углов, которые его образуют, имея общую точку. При этом они не должны лежать в одной плоскости.
У многогранного угла есть два свойства:
- сумма плоских углов многогранного угла превышает 360 градусов;
- существует плоскость, пересекающая все ребра многогранного угла.
По количеству граней многогранные углы делят на трехгранные, четырехгранные, пятигранные и так далее.
Самым показательным примером многогранного угла является вершина четырехугольной пирамида. Многогранный угол может быть невыпуклым и выпуклым.
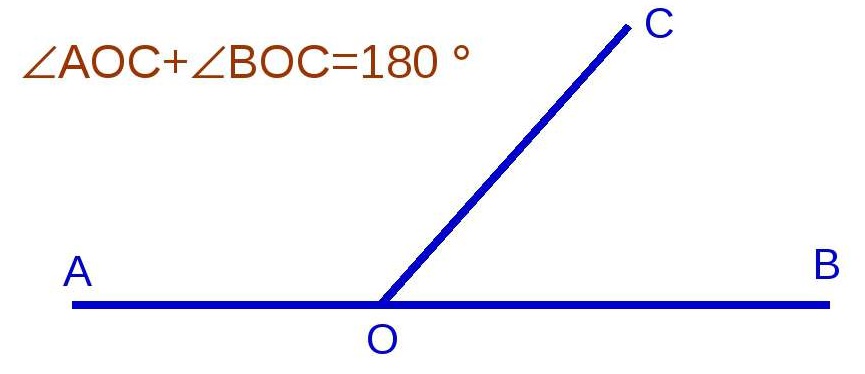
Смежные углы
Смежными называются углы, которые имеют одну общую сторону, а две другие их стороны являются продолжением друг друга. Сумма смежных углов равна 180 градусам. Поэтому, если известно значение одного угла, то найти значение второго не составляет труда.
Рисунок 9. Пример смежных углов
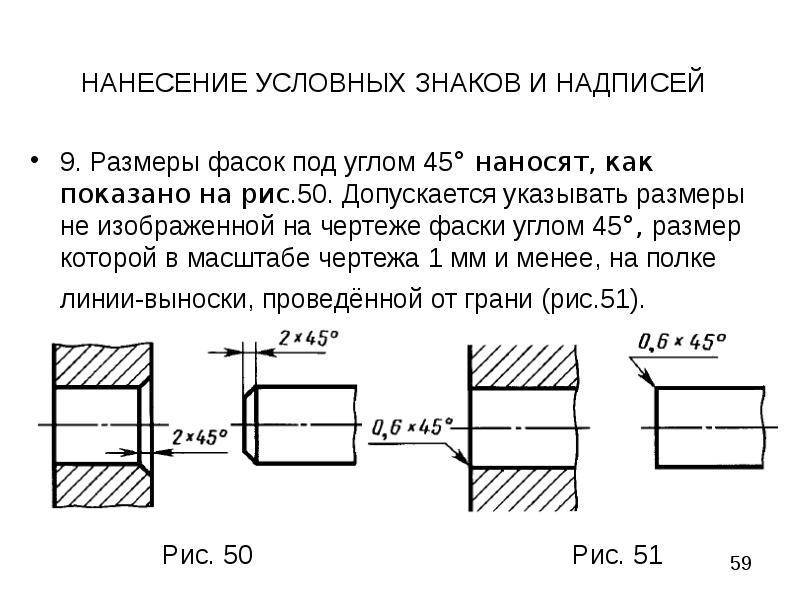
Углы фаски
Деталь может иметь скос или скругление, которое называется фаской. Обозначение фаски установлено в ГОСТ 2.307-2011, обычно ее показывают размерными линиями. Запрещено использовать осевые и контурные линии для обозначения фаски. На чертеже обязательно указывают ширину, размер скоса и угол относительно главной оси элемента или механизма. Если на чертеже показана фаска, но не указан угол, то подразумевается ее стандартное значение 45 градусов. Обозначение выполняется с помощью выносной линии или с помощью линейных размеров.
Рисунок 10. Обозначение фаски по ГОСТ
Внешние углы на чертеже
На чертежах может потребоваться указать внешний угол треугольника, это угол смежный с любым из внутренних углов. Следовательно, у каждой вершины можно построить два равных внешних угла. Также существует теорема, доказывающая что внешний угол равен сумме двух внутренних углов, которые не смежны с ним.
Центральные углы на чертеже
Центральным называется угол, который равен градусной мере дуги, на которую он опирается. Центральный угол отличается от вписанного тем, что вершин вписанного угла лежит на окружности, и он равен половине дуги, на которую опирается. Вписанные и центральные углы имеют зависимость, например, если нарисовать их на одной окружности, то вписанный угол будет равен половине центрального, если они опираются на одну дугу. Таким образом, зная один угол, можно определить другой.
Ответы на вопросы
Как обозначается радиус окружности на чертеже?
Для обозначения радиуса используется значок R, после которого указывается значение в миллиметрах и сплошная тонкая линия со стрелкой на конце. Радиус проводят от центра окружности к обозначаемому отрезку. Обычно указывают только радиус, диаметр при необходимости можно найти путем удвоения радиуса.
Как указать прямой угол?
При обозначении острого или тупого угла в основании между лучами проводят полукруг, если угол прямой в его основании рисуют квадрат.
Как отсчитывают угол на чертеже?
Угол образовывается двумя лучами, чтобы найти его значение используют транспортир.
-
Подскажите, как рассчитать угол под которым запиливать детали для создания чего-то подобного, что на картинке.
Интересует сам метод, чтобы в будущем считать самому.Вложения:
-
-
убийца,
-
Satanas, малка есть ))) Вопрос в расчёте угла пропила при помощи обычной математики. Ну т.е. есть параметры изделия которое надо сделать, как рассчитать углы?
———- Сообщение добавлено 16.06.2015 16:21 ———-
evrei34, Точно по такому же и учился ))) Раздел как называется куда смотреть? ))))
-
убийца, С 1й по178 страницу…
Дальше муть… -
KeyB
Активный участниквозможно я плохо понимаю в чем собственно вопрос, но на картинке 360*/к-во углов/2
-
KeyB
Активный участникубийца, если верхний торец и нижний торец – прямоугольникиквадраты, то почему не 45-то?
-
А у верхней фигуры стороны толщина каждой стороны не одинаковая. Т.к. угол каждой детали разный, то длина спила получается разной. На картинке изобразил. Это детали одной толщины под разным углом к плоскости.
Вложения:
-
-
pmb
Активный участникубийца, угол на который нужно кромки срезать чтобы стороны нормально прилегли?
Перпендикуляр из дальнего угла к нужной стороне, с другой стороны тоже самое, получаешь треугольник, находишь нужный угол -
очень давно тому назад я раскрой примерно таких же по форме бункеров посчитал карандашом на бумажке, при помощи формулы про пифагоровы штаны, примененной к проекциям на основания….
Причем и квадратные корни вычислял вручную, без всяких калькуляторов..
Правда нынче эту методику уже благополучно забыл, о чем жалею..сейчас есть эксел и всё гораздо проще
-
Да.
Попытался понять, но не могу.———- Сообщение добавлено 16.06.2015 18:10 ———-
Ну теорему то я знаю, только не могу понять как её применить.
-
KeyB
Активный участникну тут по двум катетам через тангенс находим угол – ca. 35,22
-
убийца,
Ваще не понял вопроса. Эскиз в скетчупе же сделан? Бери транспортир да меряй. -
KeyB,
Какая разница где мерять? Если эскиз по размерам правильно нарисован, то и угол будет правильный. -
убийца, Возьми линейку и нарисуй на листике. Сначала положи линейку и обведи один ее конец – это первая сопрягаемая сторона. Потом поверни линейку, совмести углы и обведи еще раз – получится вторая сопрягаемая сторона. Стороны касаются друг друга в углу и пересекаются на противоположной стороне. Соедини эти 2 точки прямой – дальше поймешь как найти угол
-
Прошу прощения, надо было сразу так сделать. Вот видео этой фигуры с разных сторон.
Чтобы было понятно – засада в том, что центры верхнего отверстия смещён от оси фигуры. http://youtu.be/pgUU-PRLmnM———- Сообщение добавлено 16.06.2015 19:02 ———-
———- Сообщение добавлено 16.06.2015 19:04 ———-
panda-34, не прокатит. У меня верхний и нижний край детали тоже соответственно выровнены и параллельны друг другу. Угол будет другим.
-
KeyB
Активный участникубийца, а можно вид сверху с размерами и высоту, что-то у меня не стыкуется с выложенной раскладкой, вообще, есть предположение, что углы однозначно видны на развертке, во всяком случае оч.похожи.
-
сделай проекцию угла на основание и определи угол…как то так…
Вложения:
-
-
Толщина материала из которого делается “это” – 18 (хотя на угол это влияет)
———- Сообщение добавлено 16.06.2015 20:20 ———-
evrei34, сейчас попробую, но кажется вы гений
-
egoistka, брют – отстой! Я даже когда пил, брют ненавидел! ))))
———- Сообщение добавлено 16.06.2015 21:08 ———-
WadikBOSC, спасибо!
-
Начертательной геометрией воспользоваться надо.
У меня была похожая задача. Есть крыша угол 45 г., две грани стыкуются, образуя ендову.
Какой угол будет? Сначала попробовал вывести формулу — заманался.
Потом думаю, у меня же модель есть, ранее склеенная из картона. Дайка измерю. Ок. Результат есть, но меня не радует — не по инженерному как то.
Потом думаю, у меня же проекции в автокаде нарисованы, это готовый эпюр Монжа. Делов то, построить плоскость перпендикулярно ребру и отобразить на нее грани. Ок, начертил, измерил угол.
С моделью разошлось на полградуса.
Вот.
А начерталку я сдавал 28 лет назад.
- Закрыть Меню
-
Волгоградский форум
- Поиск сообщений
- Последние сообщения
-
Пользователи
- Выдающиеся пользователи
- Зарегистрированные пользователи
- Сейчас на форуме
- Поиск
Особенности построения – Построение уклона и конусности
- Подробности
- Категория: Инженерная графика
Страница 5 из 6
ПОСТРОЕНИЕ УКЛОНА И КОНУСНОСТИ
ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ УКЛОНА
Уклоном называют величину, характеризующую наклон одной прямой линии к другой прямой. Уклон выражают дробью или в процентах.
Уклон i отрезка ВС относительно отрезка ВА определяют отношением катетов прямоугольного треугольника АВС (рис. 69, а), т. е.
Для построения прямой ВС (рис. 69, а) с заданной величиной уклона к горизонтальной прямой, например 1:4, необходимо от точки А влево отложить отрезок А В, равный четырем единицам длины, а вверх отрезок АС, равный одной единице длины. Точки С и В соединяют прямой, которая дает направление искомого уклона.
Уклоны применяются при вычерчивании деталей, например, стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем (рис. 69, д).
При вычерчивании контура детали с уклоном сначала строится линия уклона (рис. 69, в и г), а затем контур.
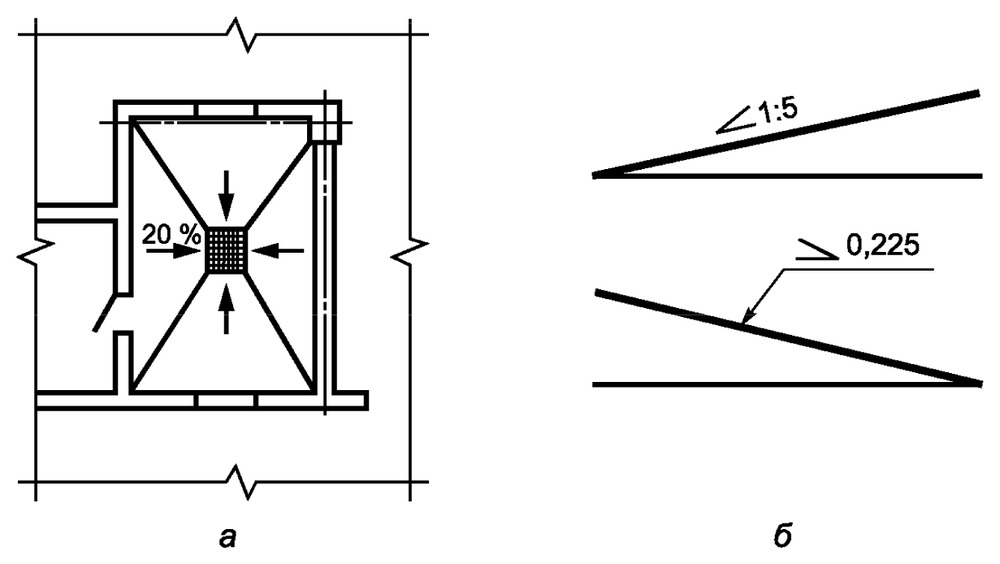
Если уклон задается в процентах, например, 20% (рис. 69, б), то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100%, а другого — 20%. Очевидно, что уклон 20% есть иначе уклон 1:5.
По ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят условный знак, острый угол которого должен быть направлен в сторону уклона (рис. 69, в и г).
ПОСТРОЕНИЕ И ОБОЗНАЧЕНИЕ КОНУСНОСТИ
На рис. 70, а даны для примера детали: оправка, конус и сверло, которые имеют конусность.
Конусностью называется отношение диаметра основания конуса к его высоте (рис. 70, б), обозначается конусность буквой С. Если конус усеченный (рис. 70, в) с диаметрами оснований D и d и длиной L, то конусность определяется по формуле:
Например (рис. 70, в), если известны размеры D=30 мм, d= 20 мм и L=70 мм, то
Если известны конусность С, диаметр одного из оснований конуса d и длина конуса L, можно определить второй диаметр конуса. Например, С=1:7,d=20
мм и L=70 мм; D находят по формуле D=CL+d= 1/7x70+20=30 мм (рис. 70, г).
По ГОСТ 2.307—68 перед размерным числом, характеризующим конусность, необходимо наносить условный знак конусности, который имеет вид равнобедренного треугольника с вершиной, направленной в сторону вершины конуса (рис. 70, в и г).
Обычно на чертеже конуса дается диаметр большего основания конуса, так как при изготовлении конической детали этот диаметр можно измерить значительно легче и точнее.
Нормальные конусности и углы конусов устанавливает ГОСТ 8593—81 (СТ СЭВ 512—77). ГОСТ 25548— 82 (СТ СЭВ 1779—79) устанавливает термины и определения.

![[IMG]](https://www.forum-volgograd.ru/threads/293542/proxy.php?image=http%3A%2F%2Fcontent.onliner.by%2Fforum%2Fd39%2Fd90%2F312062%2F800x800%2F491c331edceb4055b49e3de70fc97727.jpg&hash=c735cb6ca632dc4db76b7b1034aa0e9c)











