Уравнения предельного равновесия для сыпучих и связных грунтов
Угол наибольшего отклонения. При действии на поверхность грунта местной нагрузки в любой точке грунта М для любой площадки тп, проведенной через эту точку под углом а (рис. 64, а), возникнут нормальные и касательные напряжения. К нормальным напряжениям при математическом рассмотрении вопроса следует отнести и силы связности, суммарно оцениваемые [см. формулу (11.23′)] давлением связности рг. Тогда на площадку тп (рис. 64, а) будут действовать нормальное напряжение оа+ре и касательное Та .
При изменении угла а величина составляющих напряжений также будет меняться и, если касательные (сдвигающие) напряжения достигнут определенной доли от нормальных, то, как показывают опыты на сдвиг, произойдет скольжение одной части грунта по другой.
Таким образом, условием предельного равновесия грунта в данной точке будет
Это отношение равно тангенсу угла отклонения 9, т. е. угла, на который отклоняется полное напряжение для площадки о от нормали к этой площадке.
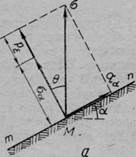
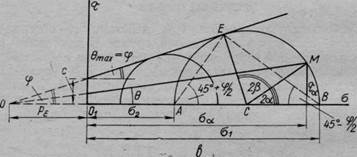
Рис. 64. Круги предельных напряжений:
а — схема напряжений в данной точке; б— диаграмма сдвига для сыпучих грунтов; в — то же, для грунтов связных
Так как через заданную точку можно провести множество площадок, то, очевидно, необходимо отыскать самую невыгодную площадку, для которой будет существовать максимальный угол отклонения бтах- Тогда
Условия предельного равновесия. Для сыпучих грунтов согласно диаграмме сдвига (см. рис. 64, б) максимальное значение угла отклонения бтах будет тогда, когда огибающая ОЕ коснется круга предельных напряжений.
Как было показано ранее (см. гл. II, § 4) и что вытекает из геометрических соотношений, поставленному условию удовлетворяет
120 равенство (11.24):
где 01 и 02 — главные напряжения;
Ф — угол внутреннего трения грунта.
Это и есть условие предельного равновесия для сыпучих грунтов. Ему можно придать несколько другой вид после несложных тригонометрических преобразований, а именно
1 — 51П ф 1 + 51Пф
Последнее выражение весьма широко используется в теории давления грунтов на ограждения, причем знак «минус» (в скобках) соответствует так называемому активному давлению, а знак «плюс» — пассивному сопротивлению сыпучих грунтов.
Условию предельного равновесия для сыпучих грунтов иногда придают иной вид, выразив главные напряжения 01 и 02 через составляющие напряжения о2, ау и хуг (для плоской задачи). Тогда будем иметь следующее выражение, тождественное зависимости (11.24):
(0у + ог) У> 1уг составляющие напряжении;
у — объемный вес грунта.
В этих двух дифференциальных уравнениях три неизвестных (ог, оу и хуг); таким образом, задача является (без добавочных условий) статически неопределимой. Если же добавить к этим двум уравнениям третье, например, (П.251У), то получим замкнутую систему трех уравнений с тремя неизвестными, но для предельного напряженного состояния, так как уравнение (П.251У) является условием предельного равновесия:
Таким образом, задача в общей постановке статически определима.
Решение дифференциальных уравнений равновесия (а1) и (аг) совместно с условием предельного равновесия (аз) в дальнейшем получено (проф. В. В. Соколовским, 1942 г.) как системы уравнений гиперболического типа.
Пространственная задача имеет замкнутую систему уравнений (статически определимую) только для случая осевой симметрии.
Для осесимметричной задачи, воспользовавшись цилиндрической системой координат (г, т>) и приняв обозначения составляющих напряжений по рис. 65, имеем следующую систему уравнений равновесия:
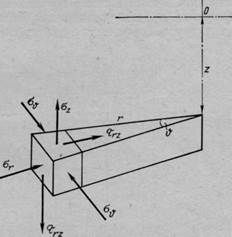
Рис. 65. Схема пространственной
напряжении в случае осесимметричной задачи
Уравнение предельного равновесия для сыпучих и связных грунтов
| УУ* 4 | ___■—7 |
| Втая = Я> / | / / V- |
| Л | |
| и / | б |
| А бы | с |
Угол наибольшего отклонения. При действии на поверхность грунта местной нагрузки в любой точке грунта М (рис. 4.4, а) для любой площадки mn, проведенной через эту точку пол углом α, возникнут нормальные и касательные напряжения. К нормальным напряжениям при математическом рассмотрении вопроса следует отнести и силы связности; суммарно оцениваемые давлением связности ре. Тогда на площадку mn (рис. 4.4, а) будут действовать нормальное напряжение σα + ре и касательное τα.
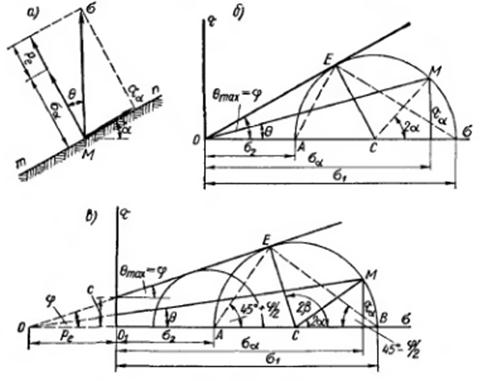
Рис. 4.4. Круги предельных напряжений: а – схема напряжений в данной точке; кривые сдвига для сыпучих (б) и связных (в) грунтов
При изменении угла α величины составляющих напряжений также будут меняться, и если касательные (сдвигающие) напряжения достигнут определенной доли от нормальных, то, как показывают опыты на сдвиг, произойдет скольжение одной части грунта по другой.
Таким образом, условием предельного равновесия грунта в данной точке будет
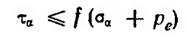
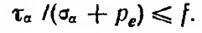
Если f — величина постоянная, то в предельном состоянии она представляет собой тангенс угла наклона прямолинейной огибающей кругов предельных напряжений (рис. 4.4, б,в).
С другой стороны, согласно рис. 4.4, а

Это отношение равно тангенсу угла отклонения Θ, т. е. угла, на который отклоняется полное напряжение для площадки σ от нормали к этой площадке.
Так как через заданную точку можно провести множество площадок, то, очевидно, необходимо отыскать самую невыгодную площадку, для которой будет существовать максимальный угол отклонения Θmax. Тогда

Условия предельного равновесия. Для сыпучих грунтов согласно диаграмме сдвига (рис. 4.4, б) максимальное значение угла отклонения Θmax будет тогда, когда огибающая ОЕ коснется круга предельных напряжений.
Из геометрических соотношений вытекает, что поставленному условию удовлетворяет равенство:
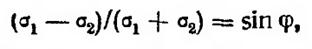
где σ1 и σ2 —главные напряжения; φ — угол внутреннего трения грунта.
Это и есть условие предельного равновесия для сыпучих грунтов. Ему можно придать несколько другой вид после несложных тригонометрических преобразований, а именно
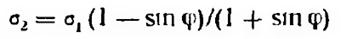

Последнее выражение весьма широко используется в теории давления грунтов на ограждения, причем знак минус (в скобках) соответствует так называемому активному давлению, а знак плюс – пассивному сопротивлению сыпучих грунтов.
Условию предельного равновесия для сыпучих грунтов иногда придают иной вид, выразив главные напряжения σ1 и σ2 через составляющие напряжения σz, σy и τzy (для плоской задачи). Тогда будем иметь выражение:
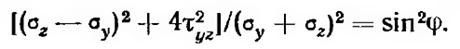
Для связных грунтов, подобно предыдущему, пользуясь кривой предельных напряжений (рис. 4.4,в), получим условие предельного равновесия в виде
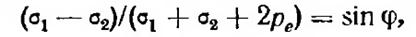
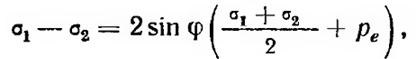 (2.25)
(2.25)
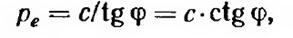
где с—сцепление грунта, определяемое как начальный параметр огибающей кругов предельных напряжений, то уравнение (2.25) может быть представлено в виде
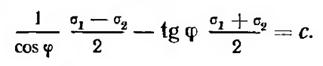
Последняя формула широко используется в задачах теории предельного равновесия.
Условие предельного равновесия в составляющих напряжениях σz, σy и τzy для связных грунтов имеет следующий вид:

Отметим, что круг предельных напряжений дает возможность определить направления площадок скольжения для любой заданной точки.
Если соединить точку касания предельной прямой ОЕ (рис. 4.4, в) с концом отрезка, изображающего в масштабе σ2 (точка А), то направление ЕА определит направление площадки скольжения. По рис. 4.4, в


Таким образом, в условиях предельного равновесия площадки скольжения будут наклонены под углом ±( 45°+ φ/2)к направлению площадки наибольшего главного напряжения, или, что то же самое, под углом ±(45°—φ/2) к направлению главного напряжения σ1.
Дата добавления: 2015-01-29 ; просмотров: 276 ; Нарушение авторских прав
Условия предельного равновесия (условия прочности) сыпучих и связных грунтов
1. Для сыпучих грунтов (различного рода пески, крупнообломочные грунты, галечники). Зависимость σ – τ принимается прямой, проходящей через начало координат и наклонной к оси нормальных напряжений σ под углом внутреннего трения φ
Указанная зависимость – условие прочности грунта (закон Кулона) для сыпучих тел: сопротивление сыпучих грунтов сдвигу есть сопротивление трения, прямо пропорциональное нормальному давлению.
2. Для связных грунтов (пылевато-глинистые грунты) прямая σ – τ не проходит через начало координат, а отсекает отрезок c на оси τ, так как в связных грунтах, обладающих сцеплением между частицами, при отсутствии нормального давления (σ = 0) сопротивление грунта сдвигу больше нуля, что обусловливается силами сцепления
Общее сопротивление сдвигу связного грунта можно выразить уравнением:
Таким образом, сопротивление связного грунта сдвигу складывается из сопротивления трения, пропорционального нормальному давлению, плюс сцепление, не зависящее от давления.
Структурно-фазовая деформируемость грунтов. Принцип линейной деформируемости.
При не очень больших изменениях внешних давлений (порядка 100…300Па для обычных и до 500..700Па для плотных грунтов) с достаточной для практических целей точностью зависимость между деформациями ε и напряжениями σ может приниматься линейной. В этом случае для определения напряжений в грунтах применимы решения теории упругости.
Профессор Н.М.Герсеванов в 1931г. сформулировал принцип линейной деформируемости:
При небольших изменениях давлений грунты можно рассматривать как линейно деформируемые тела, т.е. с достаточной для практических целей точностью можно принимать зависимость между общими деформациями и напряжениями для грунтов линейной.
Распределение напряжений в грунтовой толще от действия сосредоточенной силы. Способ элементарного суммирования.
Определение напряжений в грунтовой толще от действия внешних нагрузок необходимо для установления условий прочности и устойчивости грунтов, определения деформаций и осадок оснований фундаментов.
В большинстве практических случаев при решении вопроса о распределении напряжений в грунтах в механике грунтов применяют теорию линейно деформируемых тел. Для определения напряжений по этой теории будут полностью справедливы уравнения теории упругости, также базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука).
[spoiler title=”источники:”]
http://lektsii.com/1-91394.html
http://megaobuchalka.ru/6/43059.html
[/spoiler]
- Адиабатический процесс. Уравнение Пуассона.
- Анализ инженерно-геологических условий, анализ инженерных свойств грунтов.
- Бегущие волны описываются [1] волновым уравнением
- Безусловное торможение. Сущность внешнего и запредельного торможения. Условное торможение, его виды.
- Билет. Условия равновесия совершенно-конкурентной фирмы в долгосрочном периоде.
- Бюджетные ограничения. Изменение покупательной способности потребителя. Условие потребительского равновесия
- В приближении идеального газа уравнение Клапейрона -Клаузиуса примет вид
- Введение Задача курса механики грунтов.
- Величины ∆G , ∆F, ∆μ (и все их вариации), характеризующие меру отклонения системы от равновесия, называются движущей силой кристаллизации.
- Взаимосвязь между различными константами равновесия.
Для
оценки прочности оснований, устойчивости
грунтовых массивов и откосов, а также
давления грунтов на сооружения используют
теорию предельного напряженного
состояния. В основу этой теории положено
понятие о предельном равновесии грунта.
Предельным
равновесием основания называют такое
напряженное состояние, при котором
незначительное увеличение внешней
нагрузки приведет к нарушению
установившегося равновесия и вызовет
потерю устойчивости грунта, сопровождающееся
выпором грунта из-под подошвы сооружения
со значительным нарастанием осадки.
В
зависимости от величины внешней нагрузки
на грунт различают два понятия:
допредельное и предельное. Первое
характеризуется вполне определенными
деформациями, изменение которых может
произойти из-за повышения уровня
напряжений или в результате временных
эффектов (консолидации, ползучести).
Приближенно
можно полагать, что в диапазоне
допредельных напряженных состояний,
относительно «далеких» от предельного,
справедлива линейная связь между
напряжениями, подобная закону Гука.
Отсюда следует возможность использования
в механике грунтов решений теории
упругости.
Второе
состояние характеризуется достижением
напряжениями такой критической
комбинации, при которой устанавливается
предельное равновесие между внешней
нагрузкой и внутренними силами
сопротивления грунта.
Наступление
предельного равновесия основания может
быть вызвано различной комбинацией
напряжений, в зависимости от которой
различают условия предельного состояния,
или, как их иногда называют, теории
прочности.
Для
изучения прочности грунта в условиях
сложного напряженного состояния
применяют два основных условия (теории):
условие
, согласно которому предельное состояние
наступает при отдельном соотношении
касательного и нормального напряжений,
действующих на одной площадке;
условие
Мизеса — Шлейхера, согласно которому
предельное состояние наступает при
определенном соотношении интенсивности
касательных напряжений и среднего
нормального напряжения.
Остановимся
на теории Кулона — Мора. Пусть к граням
элементарного объема грунта приложены
главные напряжения σ1≥σ2≥σ3 (рис. 8.1,а).
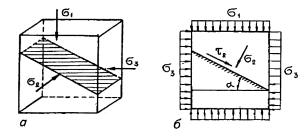
Рис.
8.1. Положение площадки скольжения (а) и
напряжения на наклонной площадке (б)
Увеличивая
постепенно главное напряжение σ1 и
оставляя постоянной величину 0-3, в
соответствии с теорией Кулона — Мора
произойдет сдвиг по некоторой площадке,
наклоненной к горизонтальной плоскости,
причем промежуточное главное напряжение
σ2 будет действовать параллельно этой
площадке.
В
отличие от схемы одноплоскостного
сдвига в случае сложного напряженного
состояния положение этой площадки
неизвестно. В теории Кулона — Мора
принимается, что на площадке скольжения
выполняется условие для несвязных или
для связных грунтов. Для того чтобы
определить положение площадки скольжения,
воспользуемся известными из сопротивления
материалов выражениями для касательного
и нормального напряжений на наклонной
площадке (рис. 8.1,6).
![]()
(8.1.)
![]()
(8.2)
Согласно
уравнения, на площадке скольжения эти
напряжения в предельном состоянии
будут связаны выражением![]()
(8.3)
Для
представления напряженного состояния
грунта используют графические
изображения, известные под названием
кругов Мора. Они дают возможность
исследовать напряжения на площадке с
любым наклоном, проходящим через
рассматриваемую точку.
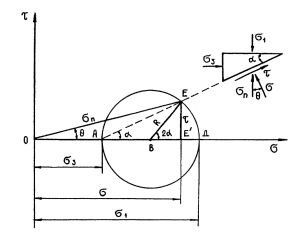
Построение
круга Мора
Круг
Мора (рис. 8.2) вычерчивается в прямоугольной
системе координат. Полагается, что
σ1≥σ2
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание страницы
- 1. Отклонения и допуски формы поверхностей
- 2. Отклонения и допуски расположения поверхностей
- 3. Суммарные отклонения и допуски формы и расположения поверхностей
- 4. Указание допусков формы и расположения поверхностей на чертежах
1. Отклонения и допуски формы поверхностей
Отклонения и допуски формы (ГОСТ24462-83)
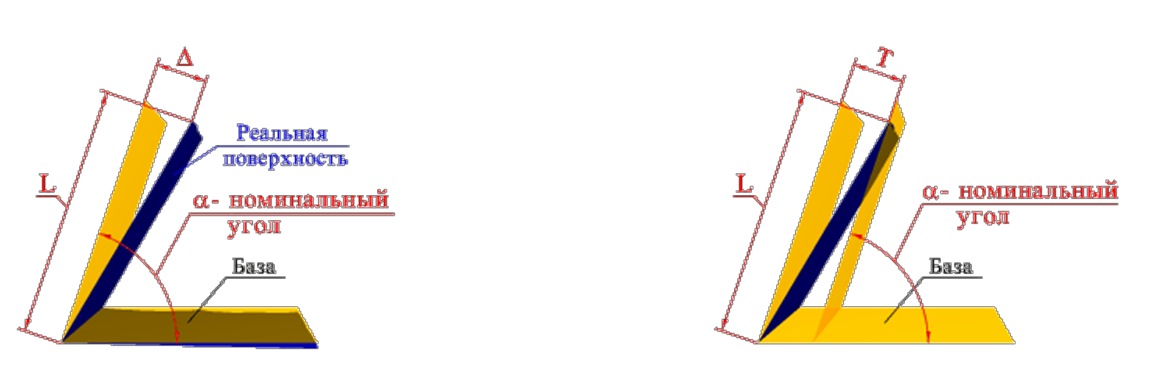
ОТКЛОНЕНИЕ ФОРМЫ — отклонение формы реальной поверхности или реального профиля от формы номинальной поверхности или номинального профиля.
СРЕДНИЙ ЭЛЕМЕНТ — поверхность (профиль), имеющая форму номинальной поверхности (профиля).
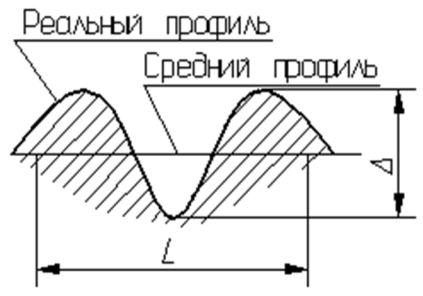
При отсчете от среднего элемента отклонение формы равно сумме абсолютных значений наибольших отклонений точек реальной поверхности (профиля) по обе стороны от среднего элемента (рис.)
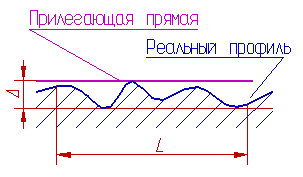
Количественно отклонение формы оценивается наибольшим расстоянием от точек реальной поверхности (профиля) до прилегающей поверхности (профиля) по нормали к прилегающей поверхности (профилю).
Допуск формы (T) — наибольшее допустимое значение отклонения формы.
Поле допуска формы — область в пространстве или на плоскости, внутри которой должны находиться все точки реального рассматриваемого элемента в пределах нормируемого участка (L).
Ширина или диаметр поля допуска определяется значением допуска, а расположение относительно реальной поверхности определяется прилегающим элементом.
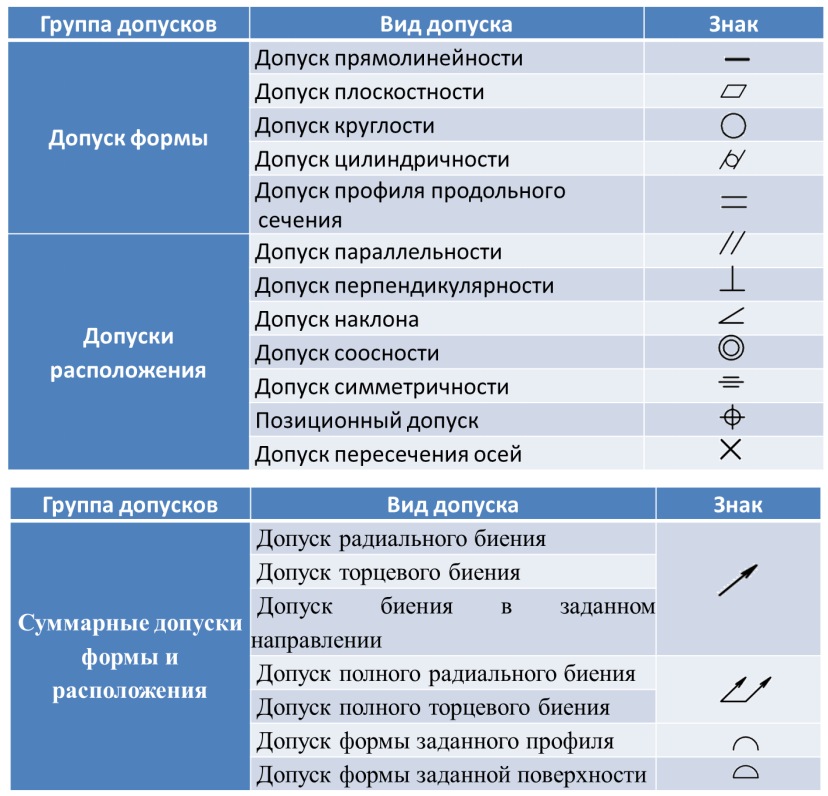
К отклонениям и допускам формы относятся:
- отклонение от плоскостности, допуск плоскостности;
- отклонение от прямолинейности, допуск прямолинейности;
- отклонение от круглости, допуск круглости;
- отклонение от цилиндричности, допуск цилиндричности;
- отклонение и допуск профиля продольного сечения цилиндрической поверхности.
Приняты следующие условные обозначения:
Δ — отклонение формы или отклонение расположения поверхностей;
Т — допуск формы или допуск расположения;
L — длина нормируемого участка.
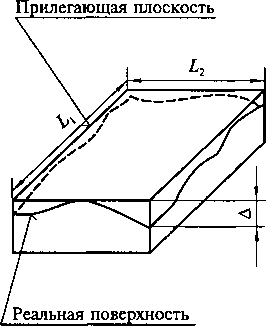
Отклонение от прямолинейности в плоскости — наибольшее расстояние от точек реального профиля до прилегающей прямой в пределах нормируемого участка.
Частными видами отклонения от прямолинейности являются выпуклость и вогнутость.
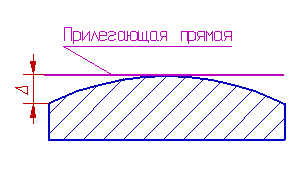
Выпуклость — отклонение от прямолинейности, при котором удаление точек реального профиля от прилегающей прямой уменьшается от краев к дине.
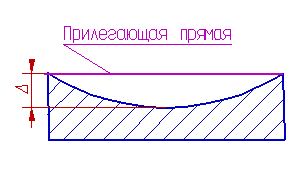
Вогнутость — отклонение от, прямолинейности при котором удаление точек реального профиля от прилегающей прямой увеличивается от краев к середине.
Отклонение от плоскостности — наибольшее расстояние Δ от точек реальной поверхности до прилегающей плоскости в пределах нормируемого участка.
Частными видами отклонения от прямолинейности являются выпуклость и вогнутость.
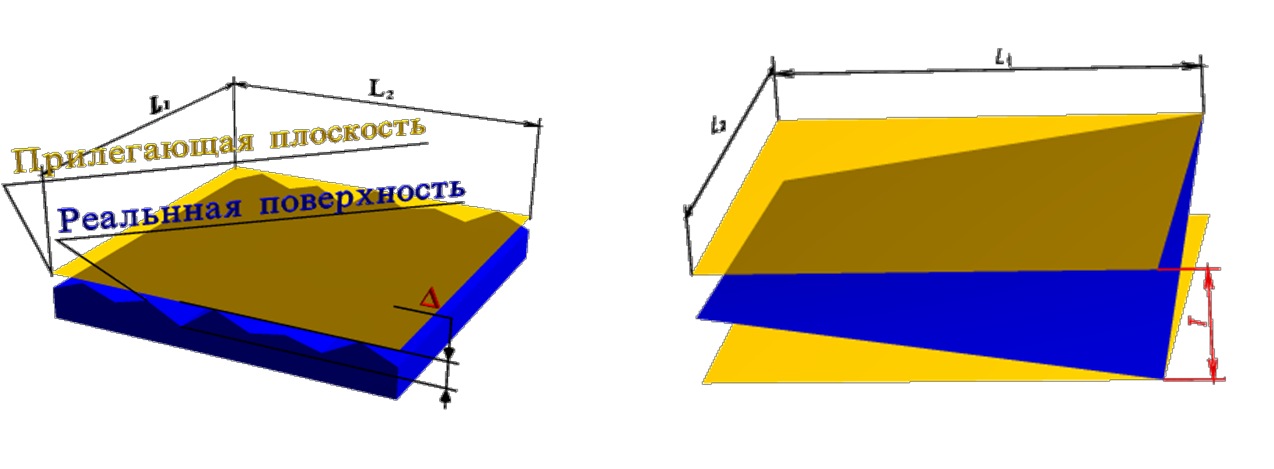
Отклонение профиля продольного сечения цилиндрической поверхности — наибольшее расстояние Δ от точек образующих реальной поверхности, лежащих в плоскости, проходящей через ее ось, до соответствующей стороны прилегающего профиля в пределах нормируемого участка.
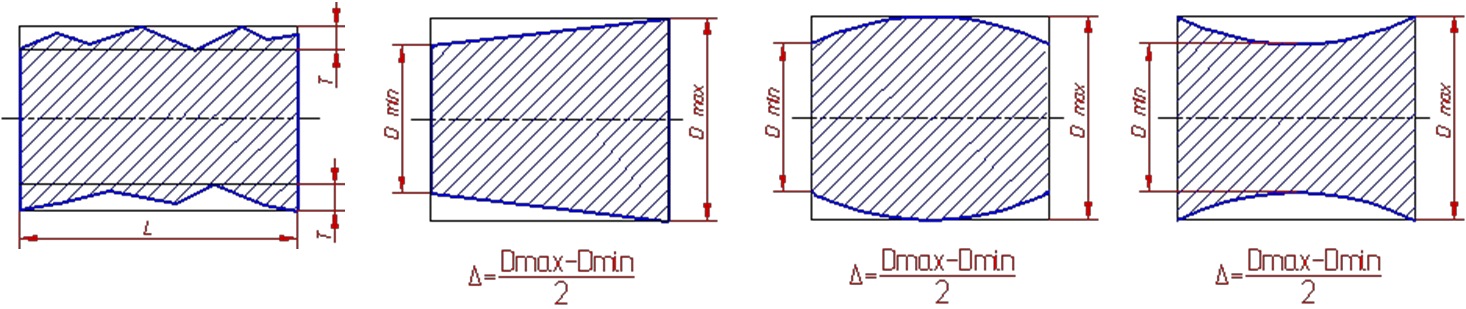
Частными видами отклонения профиля продольного сечения являются конусообразность, бочкообразность и седлообразность.
Конусообразность — отклонение профиля продольного сечения, при котором образующие прямолинейны, но не параллельны.
Бочкообразность — отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры увеличиваются от краев к середине сечения.
Седлообразность — отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры уменьшаются от краев к середине сечения.
Отклонение от цилиндричности — наибольшее расстояние Δ от точек реальной поверхности до прилегающего цилиндра в пределах нормируемого участка.
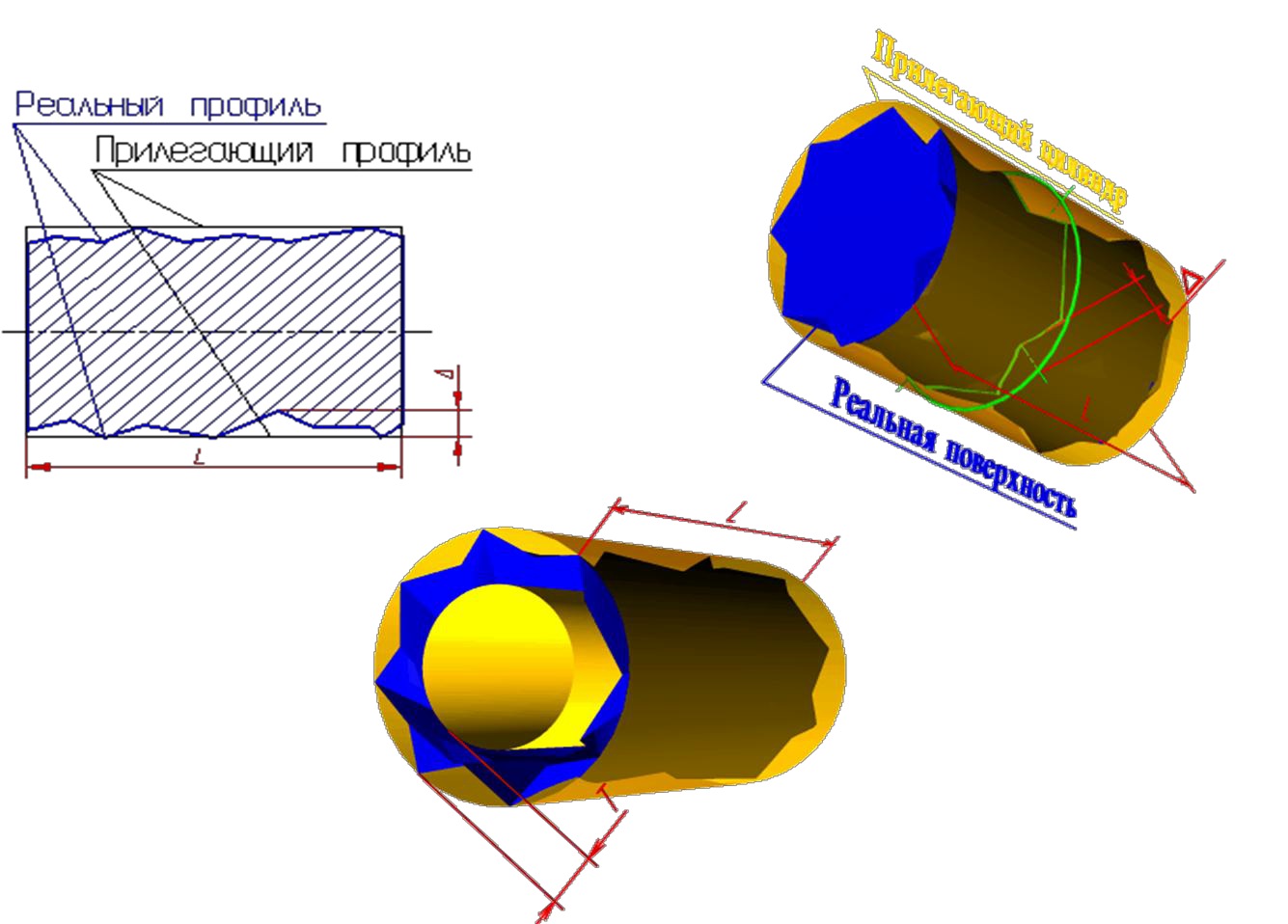
Отклонение профиля продольного сечения цилиндрической поверхности — наибольшее расстояние Δ от точек образующих реальной поверхности, лежащих в плоскости, проходящей через ее ось, до соответствующей стороны прилегающего профиля в пределах нормируемого участка.
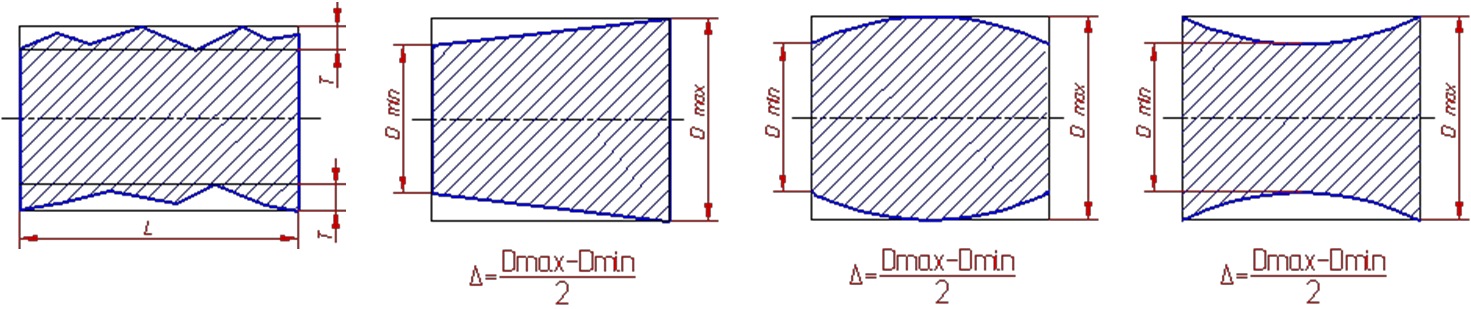
Частными видами отклонения профиля продольного сечения являются конусообразность, бочкообразность и седлообразность.
Конусообразность — отклонение профиля продольного сечения, при котором образующие прямолинейны, но не параллельны.
Бочкообразность — отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры увеличиваются от краев к середине сечения.
Седлообразность — отклонение профиля продольного сечения, при котором образующие непрямолинейны и диаметры уменьшаются от краев к середине сечения.
2. Отклонения и допуски расположения поверхностей
Отклонением расположения ЕР называется отклонение реального расположения рассматриваемого элемента от его номинального расположения. Под номинальным понимается расположение определяемое номинальными линейными и угловыми размерами.
Для оценки точности расположения поверхностей назначаются базы (элемент детали, по отношению к которому задается допуск расположения и определяется соответствующее отклонение).
Допуском расположения называется предел, ограничивающий допускаемое значение отклонения расположения поверхностей.
Поле допуска расположения ТР – область в пространстве или заданной плоскости, внутри которой должен находиться прилегающий элемент или ось, центр, плоскость симметрии в пределах нормируемого участка, ширина или диаметр которой определяется значением допуска, а расположение относительно баз – номинальным расположением рассматриваемого элемента.
Стандартом установлено 7 видов отклонений расположения поверхностей:
- от параллельности; — от перпендикулярности; — наклона;
- от соосности; — от симметричности; — позиционное;
Отклонение и допуски расположения (ГОСТ24642-83)
Отклонение от параллельности плоскостей — разность Δ наибольшего и наименьшего расстояний между плоскостями в пределах нормируемого участка
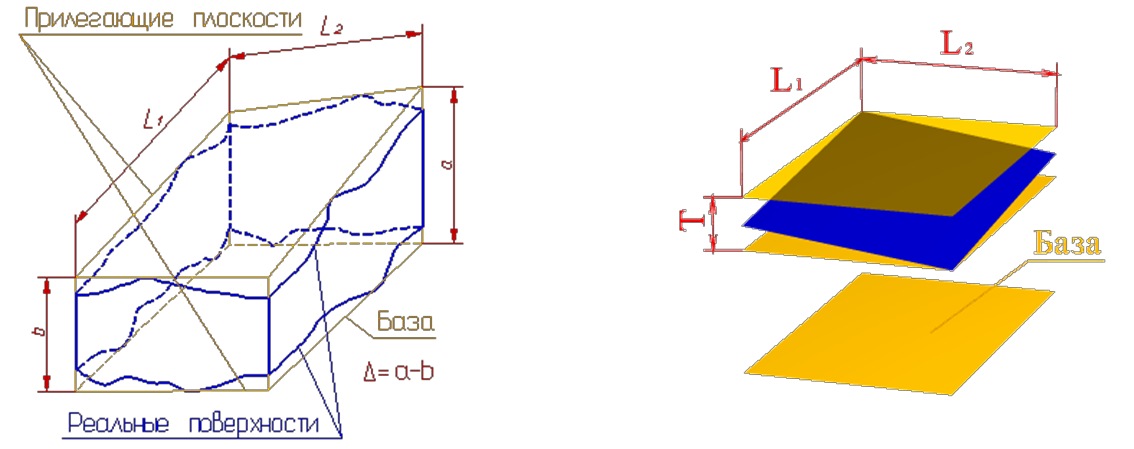
Отклонение от параллельности оси (или прямой) и плоскости — разность Δ наибольшего и наименьшего расстояний между осью (прямой) и плоскостью на длине нормируемого участка
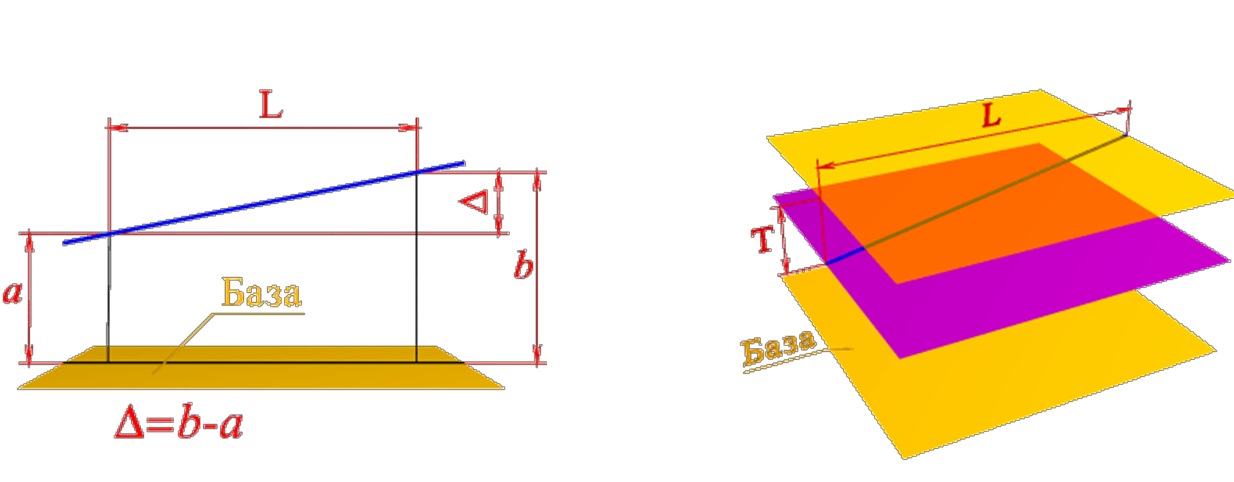
Отклонение от перпендикулярности плоскостей — отклонение угла между плоскостями от прямого угла (90°), выраженное в линейных единицах Δ на длине нормируемого участка.
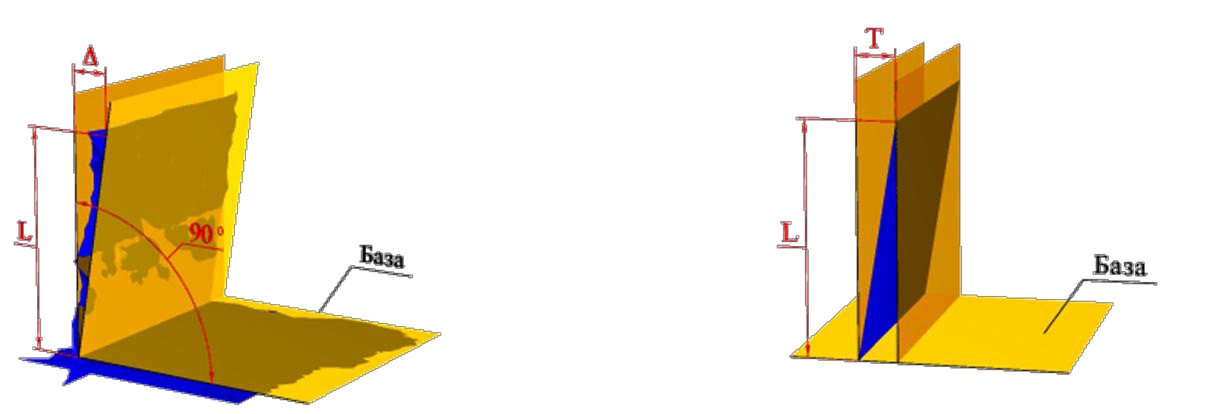
Отклонение от перпендикулярности плоскости или оси (или прямой) относительно оси (прямой) — отклонение угла между плоскостью или осью (прямой) и базовой осью от прямого угла (90°), выраженное в линейных единицах Δ на длине нормируемого участка
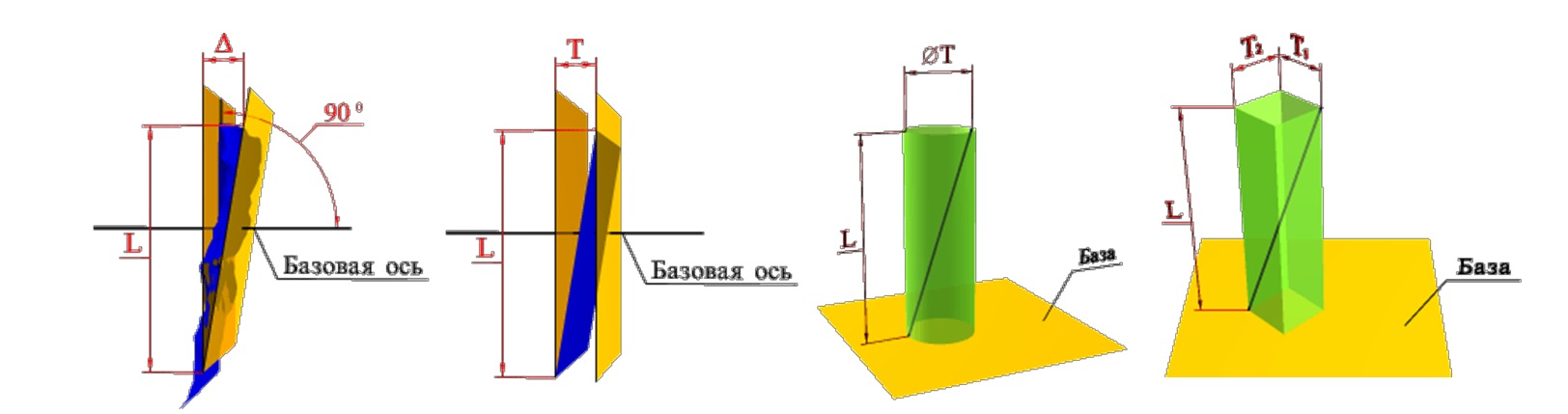
Отклонение наклона плоскости относительно плоскости или оси (или прямой) — отклонение угла между плоскостью и базовой плоскостью или базовой осью (прямой) от номинального угла, выраженное в линейных единицах Δ на длине нормируемого участка.
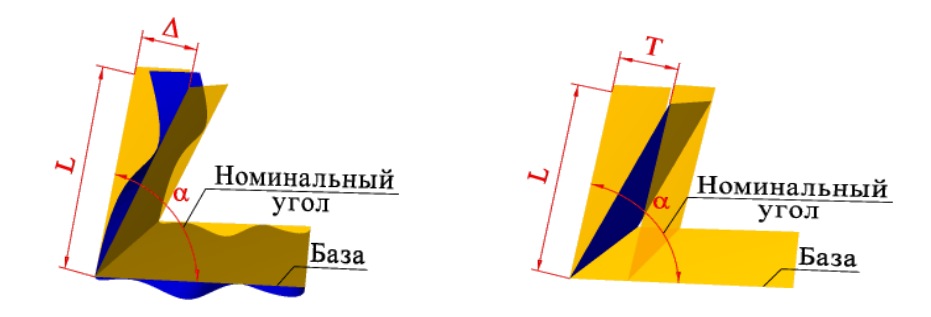
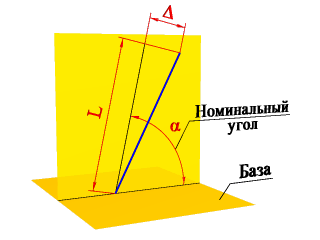
Отклонение наклона оси (или прямой) относительно оси (прямой) или плоскости — отклонение угла между осью поверхности вращения (прямой) и базовой осью или базовой плоскостью от номинального угла, выраженное в линейных единицах Δ на длине нормируемого участка.
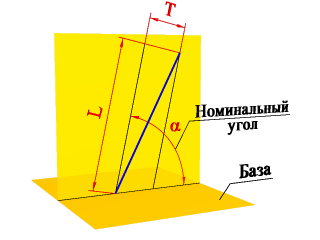
Отклонение от соосности относительно оси базовой поверхности — наибольшее расстояние Δ между осью рассматриваемой поверхности вращения и осью базовой поверхности на длине нормируемого участка.
Отклонение от соосности относительно общей оси — наибольшее расстояние (Δ 1, Δ 2,…) между осью рассматриваемой поверхности вращения и общей осью двух или нескольких поверхностей вращения на длине нормируемого участка.
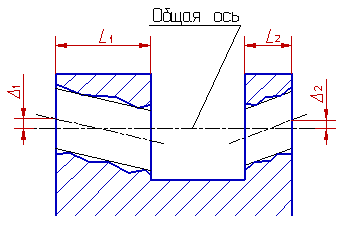
Отклонение от концентричности — отклонение от концентричности — расстояние в заданной плоскости между центрами профилей (линий), имеющих номинальную форму окружности.
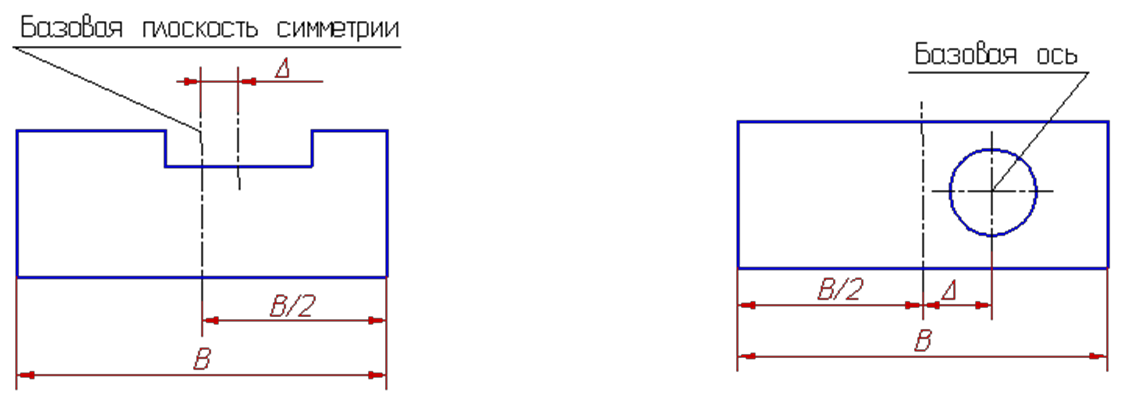
Отклонение от симметричности относительно базового элемента — наибольшее расстояние Δ между плоскостью симметрии (осью) рассматриваемого элемента (или элементов) и плоскостью симметрии базового элемента в пределах нормируемого участка.
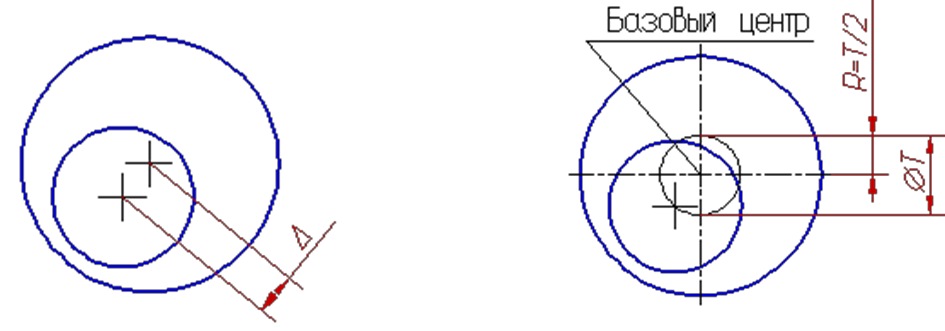
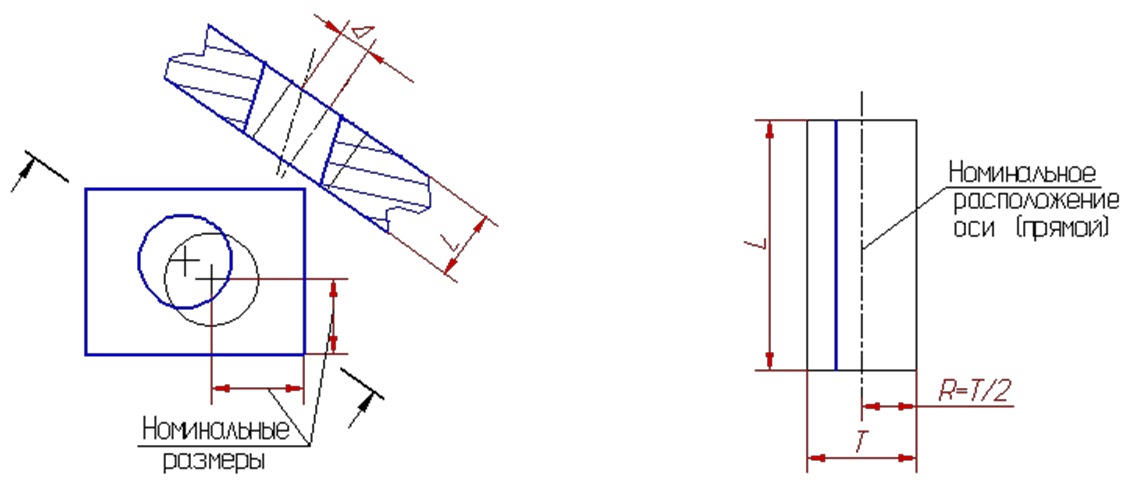
Позиционное отклонение — наибольшее расстояние Δ между реальным расположением элемента (его центра, оси или плоскости симметрии) и его номинальным расположением в пределах нормируемого участка.
3. Суммарные отклонения и допуски формы и расположения поверхностей
Суммарное отклонение формы и расположения — отклонение, являющееся результатом совместного проявления отклонения формы и отклонения расположения рассматриваемой поверхности или рассматриваемого профиля относительно заданных баз.
Суммарный допуск формы и расположения – предел ограничивающий допускаемое значение с отклонения формы и расположения.
Поле суммарного допуска формы и расположения – область в пространстве или на заданной поверхности, внутри которой должны находиться все точки реальной поверхности (профиля) в пределах нормируемого участка.
Виды суммарного отклонения и допуска формы расположения поверхностей:
- Радиальное биение и допуск радиального биения.
- Торцовое биение и допуск торцового биения.
- Биение и допуск биения в заданном направлении.
- Полное радиальное биение и допуск полного радиального биение.
- Полное торцовое биение и допуск полного торцового биения.
- Отклонение и допуск формы заданного профиля.
- Отклонение и допуск формы заданной поверхности.
Радиальное биение — разность Δ наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения до базовой оси в сечении плоскостью, перпендикулярной базовой оси.
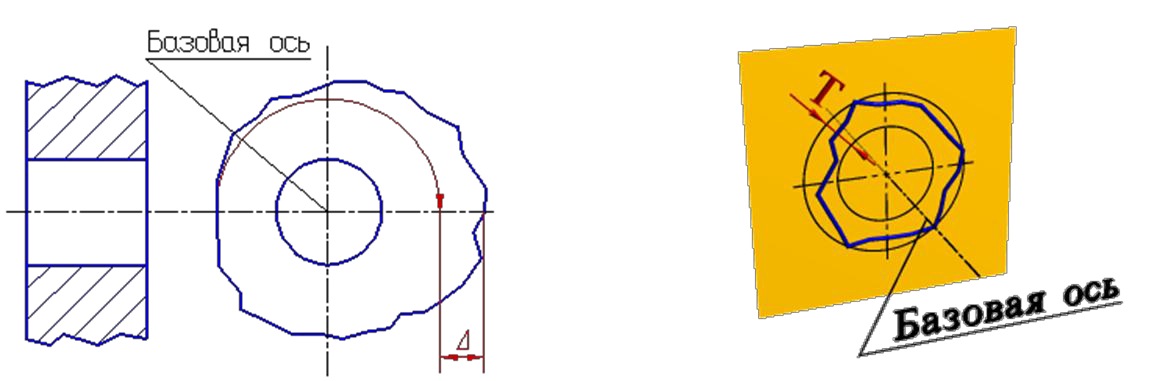
Торцовое биение — разность Δ наибольшего и наименьшего расстояний от точек реального профиля торцовой поверхности, до плоскости, перпендикулярной базовой оси.
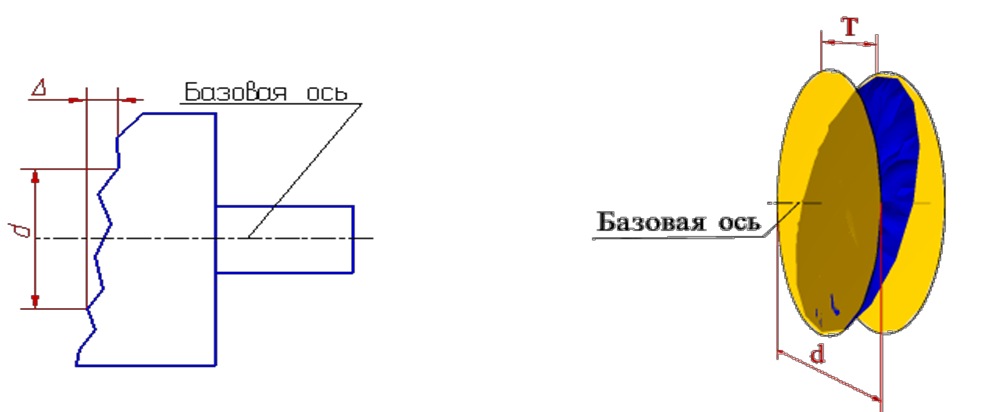
Биение в заданном направлении — разность Δ наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения в сечении рассматриваемой поверхности конусом, ось которого совпадает с базовой осью, а образующая имеет заданное направление, до вершины этого конуса.

Полное радиальное биение — разность Δ наибольшего и наименьшего расстояний от всех точек реальной поверхности в пределах нормируемого участка до базовой оси.
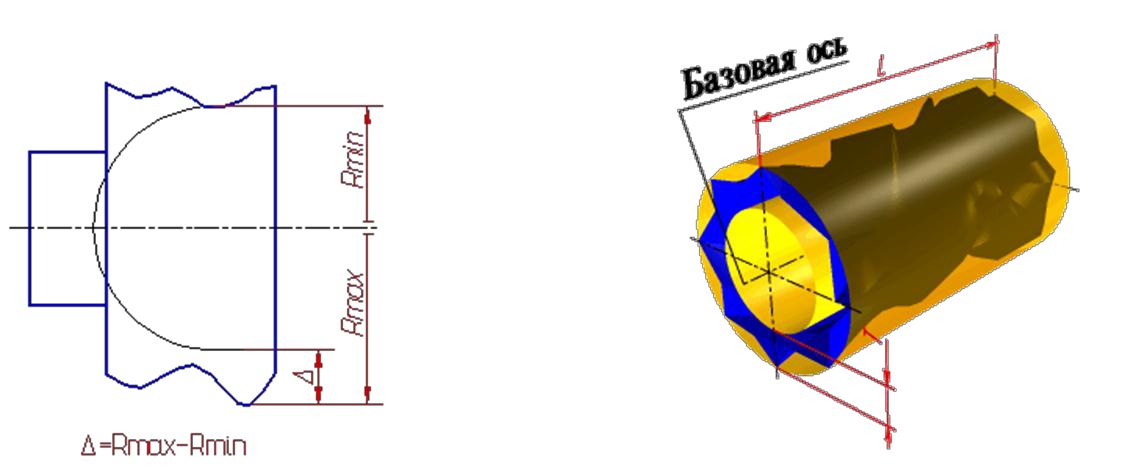
Полное торцовое биение — разность Δ наибольшего и наименьшего расстояний от точек всей торцовой поверхности до плоскости, перпендикулярной базовой оси.
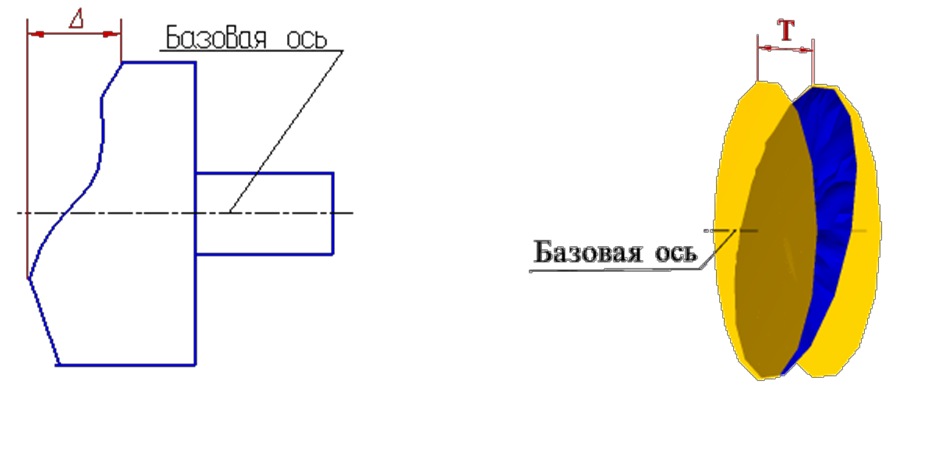
Отклонение формы заданного профиля — наибольшее отклонение Δ точек реального профиля от номинального профиля, определяемое по нормали к номинальному профилю в пределах нормируемого участка.
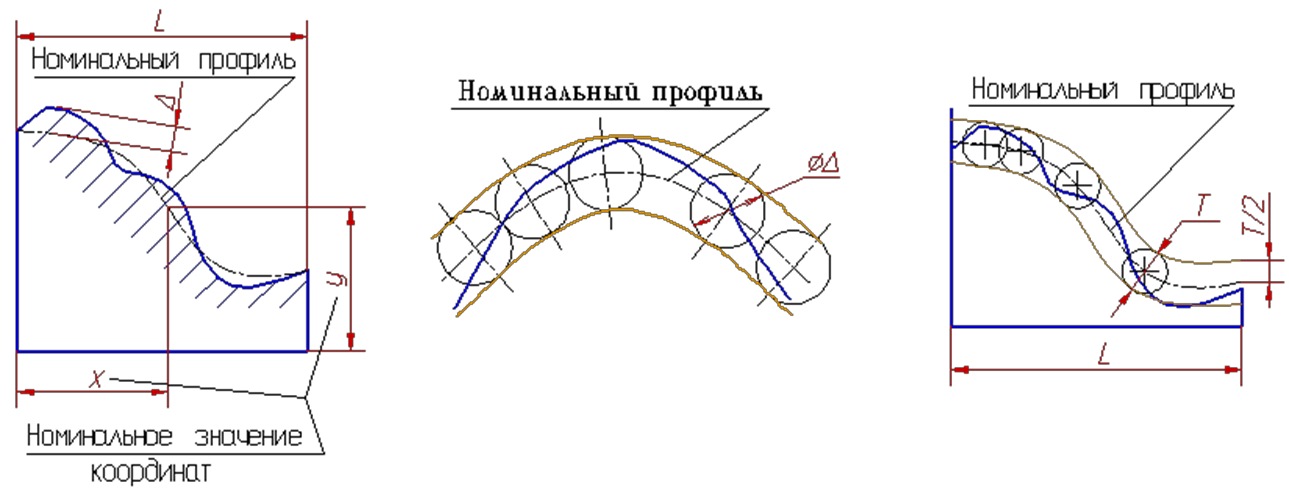
Отклонение формы заданной поверхности — наибольшее отклонение Δ точек реальной поверхности от номинальной поверхности, определяемое по нормали к номинальной поверхности в пределах нормируемого участка.
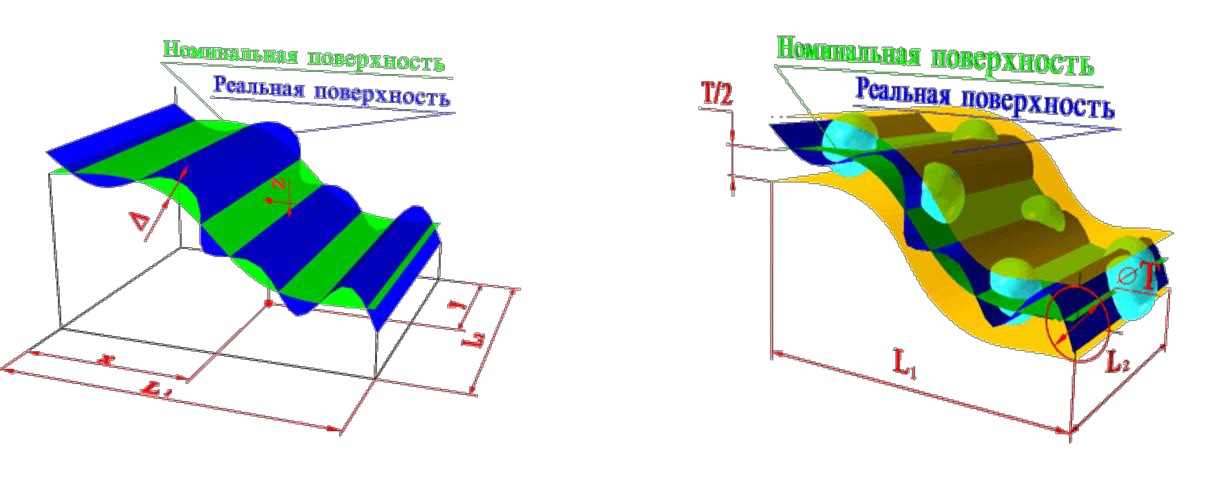
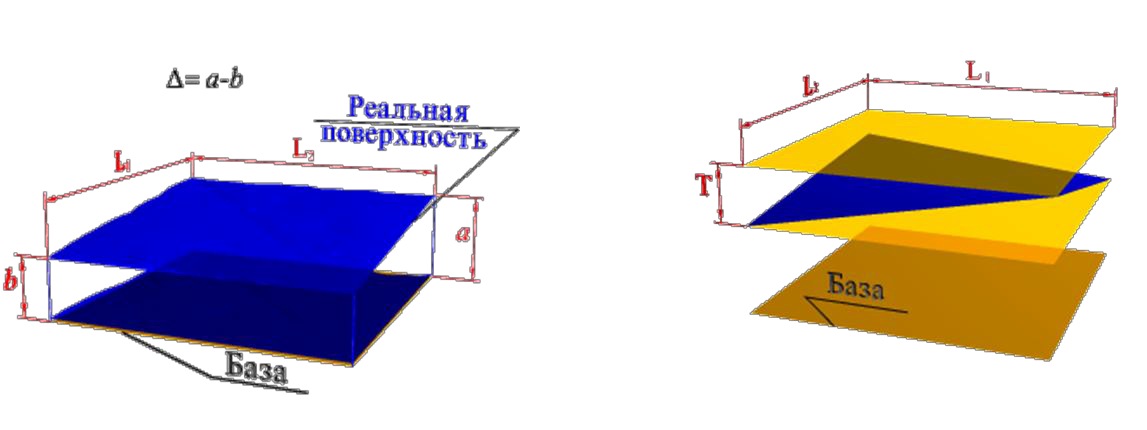
Суммарное отклонение от параллельности и плоскостности — разность Δ наибольшего и наименьшего рас стояний от точек реальной поверхности до базовой плоскости в пределах нормируемого участка.
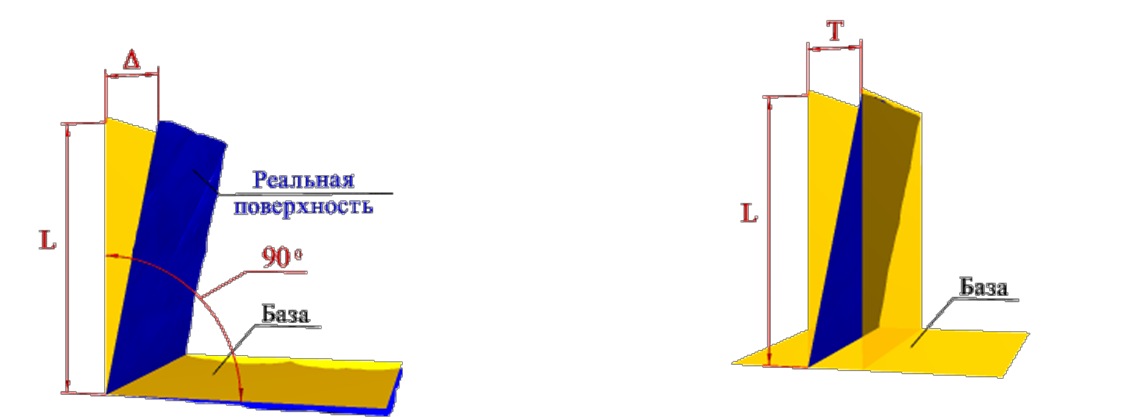
Суммарное отклонение от перпендикулярности и плоскостности — разность Δ наибольшего и наименьшего расстояний от точек реальной поверхности до плоскости, перпендикулярной базовой плоскости или базовой оси в пределах нормируемого участка.
Суммарное отклонение от номинального наклона и плоскостности — разность Δ наибольшего и наименьшего расстояний от точек реальной поверхности до плоскости, расположенной под заданным номинальным углом относительно базовой плоскости или базовой оси, в пределах нормируемого участка.
4. Указание допусков формы и расположения поверхностей на чертежах
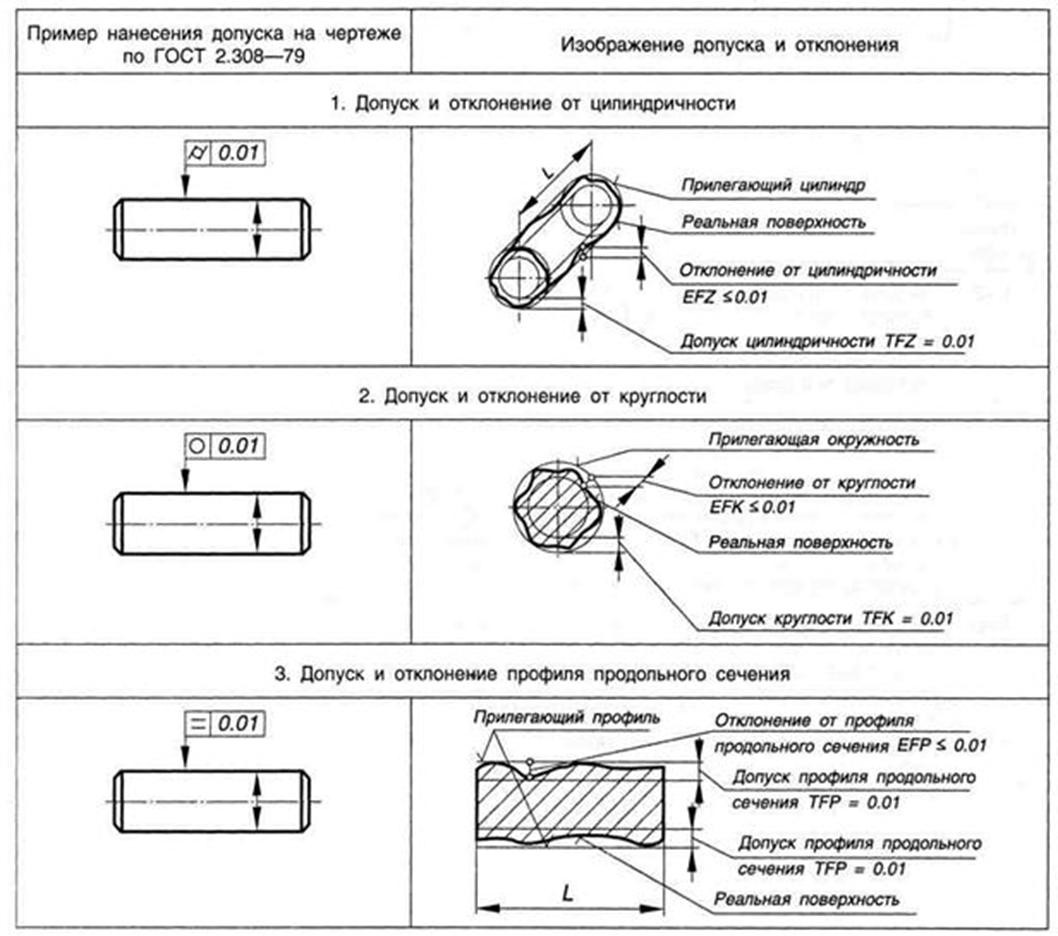
В соответствии с ГОСТ 2.308–79, вид допуска формы и расположения поверхностей должен быть обозначен в чертеже знаками (графическими символами), приведенными в таблице 1.
Таблица 1 – Классификация допусков формы и расположения по ГОСТ 24642–81 и условные знаки допусков по ГОСТ 2.308–79
Просмотров: 870

Пример решения задачи по определению угла отклонения стержня от вертикали при его вращении как функцию угловой скорости и реакций опор в заданных точках.
Задача
С невесомым валом AB шарнирно скреплен однородный стержень OD длиной l и массой m1, имеющий на конце груз массой m2.
Вал и стержень вращаются вокруг оси OZ с постоянной угловой скоростью ω. Известны b1 и b2 – расстояния от опор до точки крепления стержня (рисунок 1.4).
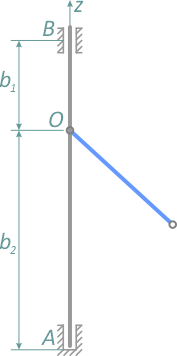
Рисунок 1.4
Требуется определить угол отклонения стержня от вертикали — α, как функцию угловой скорости и реакции опор A и B.
Другие примеры решений >
Помощь с решением задач >
Решение
Применим принцип Даламбера для данной системы. Проведем вращающиеся вместе с валом и стержнем оси координат Axyz так, чтобы стержень OD находился в плоскости yAz. Внешние силы: G1, G2; реакции опор: xA, yA, zA, xB, yB; силы инерции Φ1 и Φ2 (рисунок 1.5).
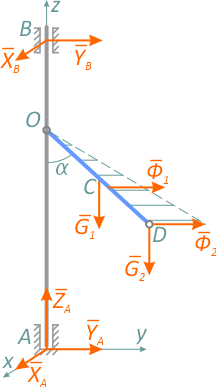
Рисунок 1.5
Отклонение стержня от вертикали происходит за счет сил инерции. Определенной угловой скорости соответствует свой угол отклонения. Величина силы инерции стержня определяется из формулы
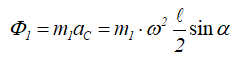
и направлена перпендикулярно к оси вращения, в сторону, противоположную ускорению центра масс стержня.
Эпюра распределения сил инерции стержня представляет собой треугольник (элементарные силы инерции частичек стержня возрастают с удалением от точки O к точке D, т.к. растет их ускорение с увеличением радиуса вращения). Результирующая таких сил приложена на расстоянии 2/3 длины стержня от точки O (см. раздел «Статика», распределенные нагрузки).
Сила инерции точечной массы
![]()
Напишем для равновесия стержня при данной угловой скорости ω уравнение моментов относительно точки O – точки крепления стержня:
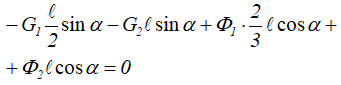
подставляем данные:
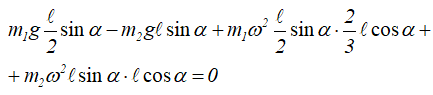
определяем угол:
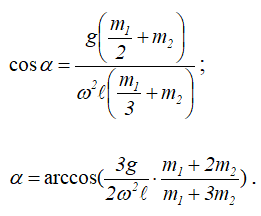
Для определения реакций опор вала составим уравнения равновесия:
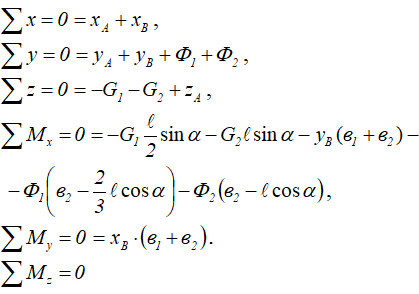
— вращающие моменты отсутствуют, система вращается по инерции, с постоянной угловой скоростью.
Из имеющихся пяти уравнений, подставляя данные задачи, можно найти пять неизвестных реакций в опорах A и B.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
