8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
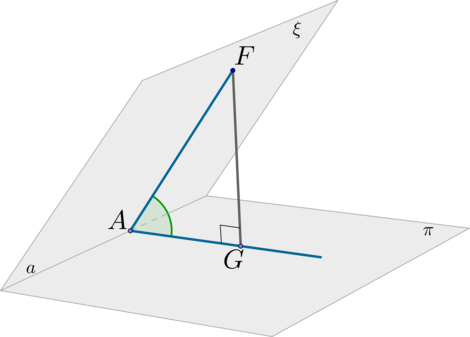
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
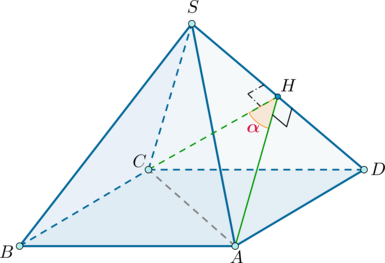
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
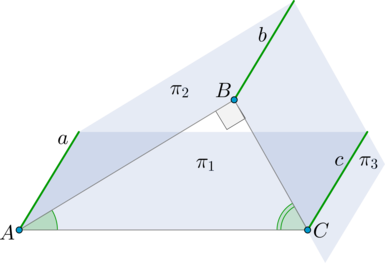
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
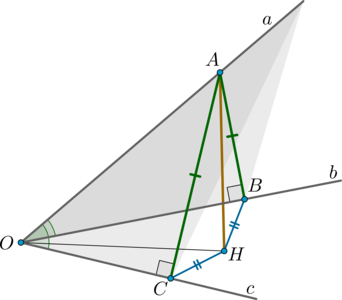
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
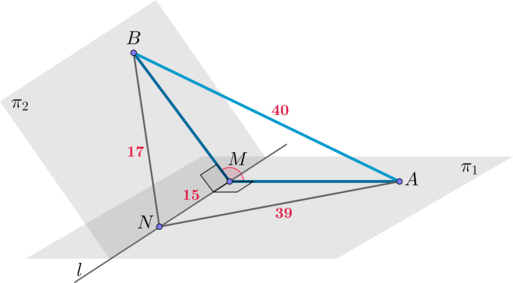
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 – 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 – 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 – 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 – 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
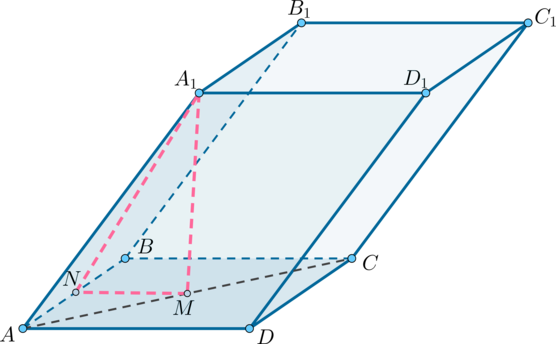
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
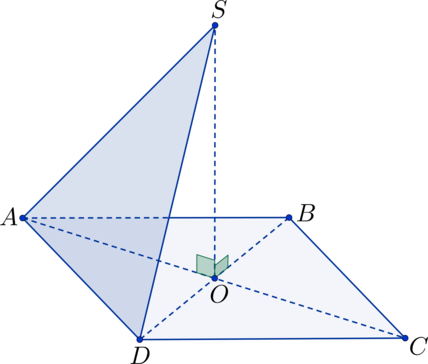
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
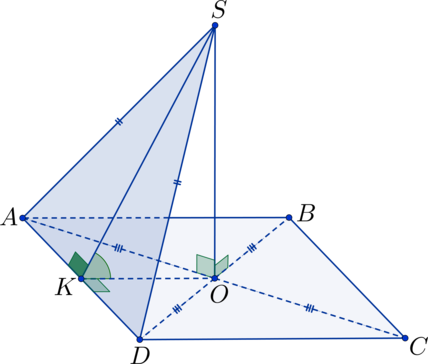
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
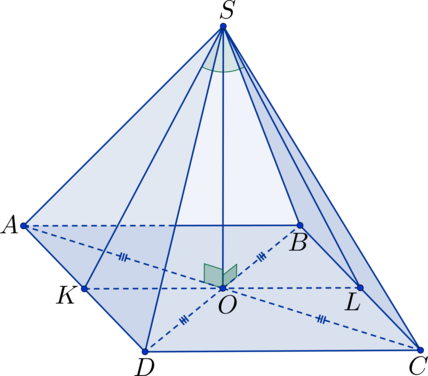
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни
Задача № 1.
Условие задачи:
Определить
углы наклона плоскости ΔАВС к плоскостям
проекций П1,
П2,
П3.Исходные
данные к задаче представлены в таблице
1.

Рисунок 1
Решение:
Задачу рассмотрим
на примере нахождения угла наклона
плоскости ΔАВС к плоскостям проекций
П1.
Алгоритм решения
задачи следующий:
1 Проводим главную
линию плоскости (линию уровня), угол
наклона к которой хотим определить,
т.е. горизонталь
h2
║x;
h2
→ h1
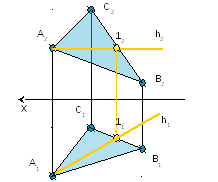
2 Проводим линию
ската перпендикулярно горизонтали
C121
┴ h1
21
→ 22

3 Определяем
натуральную величину линии ската
2120
┴ С121,
2021
= ∆Z
C120
– НВ линии ската
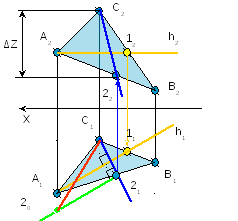
4 Определяем искомый
угол
<α
= < (С121;
С120)
; <α
– искомый
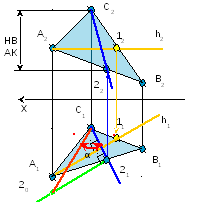
Аналогичным образом
находятся углы наклона плоскости к
фронтальной и профильной плоскостям
проекций, для чего проводятся фронталь
и профиль соответственно. Алгоритм
решения задачи сохраняется.
Задача № 2.
Условие задачи:
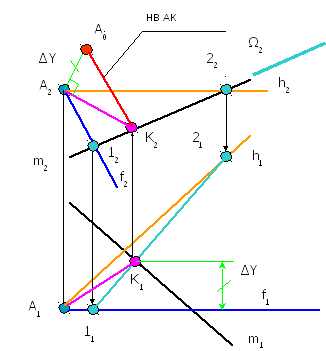
Найти расстояние
от точки D
до плоскости треугольника АВС.
Исходные данные
к задаче представлены в таблице 1.
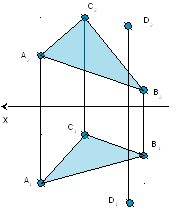
Рисунок 2
Решение:
Алгоритм решения
задачи:
1 Через точку
проводим прямую, перпендикулярную
плоскости
n
┴ P(∆ABC)
: n1┴
h1;
n2
┴ f2;
h2||х;
f1||х
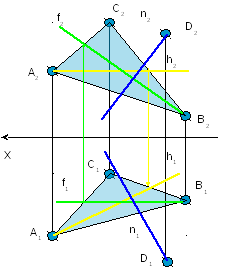
2 Определяем
основание перпендикуляра, т.е. точку
пересечения прямой и плоскости
n2
ЄΣ2,
Σ┴П2
12= Σ
∩ Р(АВС);
К1=1121
∩ n1
K1
→ K2
(·)K=n
∩ P(ABC)
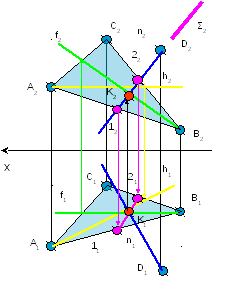
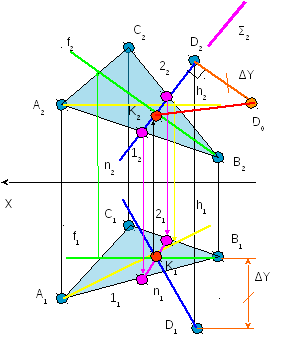
3 Находим натуральную
величину полученного отрезка
Из ∆К2D2D0
:
D2D0=
∆Y
K2D2
– проекция KD
значит – K2D0
– НВ отрезка KD
Задача № 3.
Условие задачи:
Определить
линию пересечения плоскостей, заданных
треугольниками ΔАВС и ΔDEF.
Определить видимость.
Исходные данные
к задаче представлены в таблице 1.

Рисунок 3
Решение:
Существует несколько
способов решения данной задачи.
Использовать можно любой из них. Мы
рассмотрим только один.
Для определения
линии пересечения треугольников дважды
решается задача на нахождение точки
пересечения плоскости треугольника с
прямой, принадлежащей другому треугольнику.
Через две найденные точки проводят
линию пересечения треугольников.
Алгоритм решения
задачи следующий:
1 Заключить одну
из сторон треугольника в проецирующую
плоскость. Определить точку пересечения
прямой, принадлежащей плоскости Р с
плоскостью Q.
С2В2
ЄΣ2
; Σ(Σ2)
┴ П2
1222
→ 1121
N1=1121
∩ C1B1 N1
→ N2
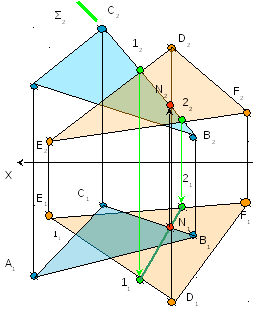
2 То же самое
проделать с другой прямой.
E1D1
Є Θ1
;
Θ(Θ1)
┴ П1
3141
→ 3242
M2=3242
∩E2D2
M2
→ M1

3 Соединить
полученные точки – это будет NM
N1M1,
N2M2
– проекции искомой линии пересечения
плоскостей

4 Определить
видимость плоскостей
Видимость на П1
:
5,3 –конкурирующие
точки. Видимой будет точка, которая
находится дальше от оси Х, т.е. 32
дальше, чем 52,
следовательно, точка 31
принадлежащая отрезку А1С1
будет видна.
Видимость на П2
:
1,6 –конкурирующие
точки. Видимой будет точка, которая
находится дальше от оси Х, т.е. 11
дальше, чем 61,
следовательно, точка 12
принадлежащая отрезку Е2D2
будет видна.
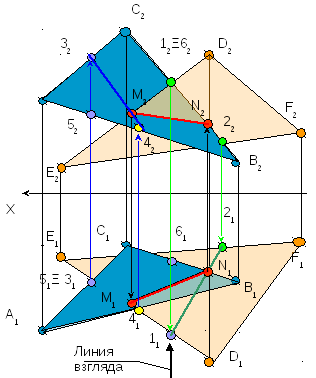
Задача № 4.
Условие задачи:
Построить
плоскость равную и параллельную плоскости
ΔАВС и отстоящую от нее на расстоянии
30 мм. Определить видимость.Исходные
данные к задаче представлены в таблице
1.
Решение:
Алгоритм решения
задачи следующий:
1 Из любой вершины
треугольника проводим прямую,
перпендикулярно плоскости ΔАВС.
n
┴ P(∆ABC)
: n1┴
h1;
n2
┴ f2;
h2||х;
f1||х
2 На прямой выбираем
произвольную точку К (К1,К2).
К1€n1,
K2€n2
3 Находим натуральную
величину отрезка СК
Из ∆К2С2К0
:
К2К0=
∆Y
K2С2
– проекция KС
значит – С2К0
– НВ отрезка KС
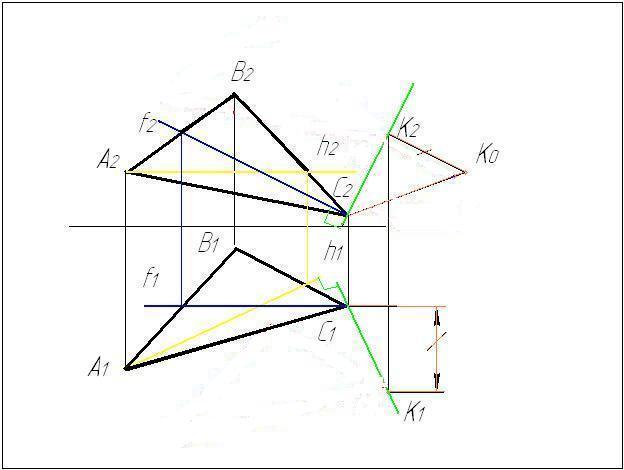
4 На натуральной
величине откладываем нужное нам
расстояние 30 мм и находим проекции новой
точки на прямой n.
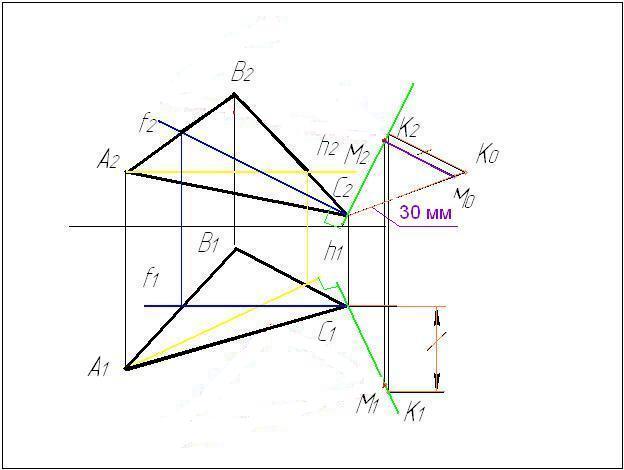
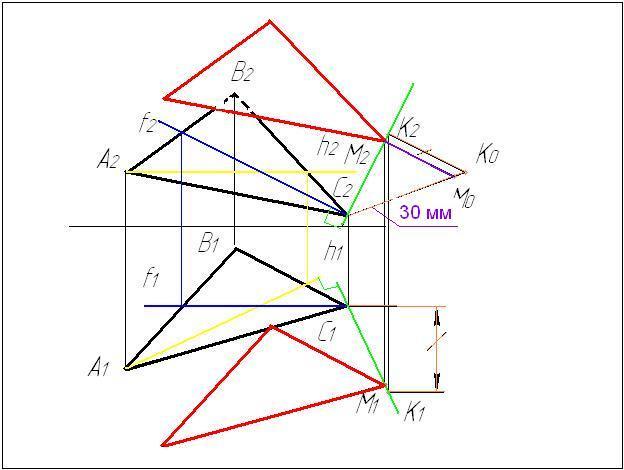
5 Через найденную
точку проводим прямые, параллельно
сторонам ΔАВС. Необходимо проконтролировать,
чтобы вершины построенного треугольника
находились в проекционной связи.
6 Определяем
видимость треугольников.
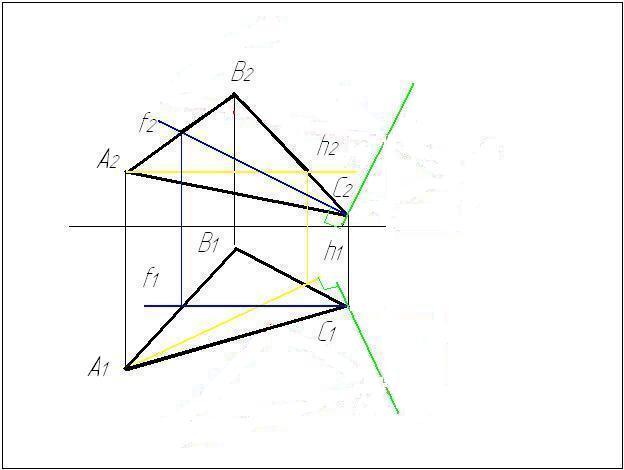
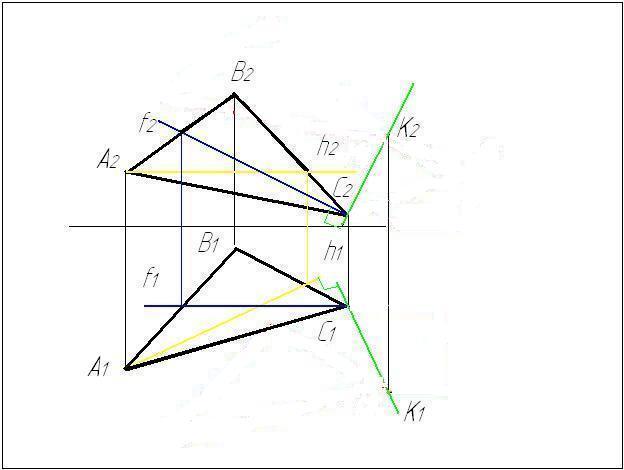
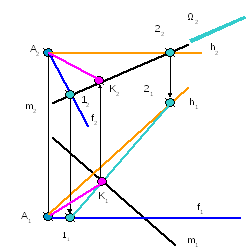
Задача № 5.
Условие задачи:
Найти расстояние
от точки А до прямой m
заданной отрезком ВС. Исходные данные
к задаче представлены в таблице 1.
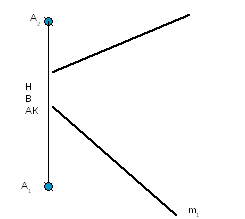
Рисунок 4
Решение:
Алгоритм решения
задачи следующий:
1 Через точку А
проводим плоскость, перпендикулярную
прямой m
(ВС).
Σ(h
∩ f):
f2
┴m2,
f1║x
h1
┴m1,
h2║x
Σ(h
∩ f)
┴ m

2 Находим точку
пересечения прямой m
и плоскости Σ(h
∩ f)
m2
Є Ω2,
Ω
┴ П2
Ω2
∩ Σ2
= 1222,
1222
→1121
1121
∩ m1
=K1,
K1
→K2
3 Определяем НВ
отрезка АК – расстояние от точки А до
прямой m
Из ∆А2К2А0
:
А2А0
= ∆Y
(A1K1)
A2K2
– проекция АК,
значит – А0К2
– НВ АК
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Угол между плоскостями
Содержание:
- Углы между плоскостями — обозначение
-
Расположение плоскостей и формула вычисления угла между ними
- Параллельность
- Перпендикулярность
- Угол между плоскостями
- Примеры решения задач
Углы между плоскостями — обозначение
Определение
Углом между плоскостями именуется такой угол, который образовался между перпендикулярными прямыми, опущенными в пределах этих плоскостей к линии их пересечения.
Рассмотрим данное понятие наглядно с помощью картинки:
Допустим, α и β — пересекающиеся плоскости. Проведем к линии с перпендикуляр a, который принадлежит α. Далее проведем прямую b, лежащую в β и образующую с прямой c угол в 90°. Угол между α и β равен углу, который образовался между а и b, обозначенному на картинке как φ. В записи это выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
∠(α, β)=∠(а, b)=φ
На схеме видно, что при пересечении α и β возникают четыре угла, но углом между плоскостями считается острый угол. В случае, когда плоскости при пересечении создают прямые углы, они считаются перпендикулярными друг другу.
Расположение плоскостей и формула вычисления угла между ними
Существует несколько вариаций взаимного расположения двух плоскостей.
Параллельность
Теорема
Две плоскости считаются параллельными в том случае, если у них отсутствуют общие точки.
Возьмем за условие, что плоскости α, расположенной в некоторой прямоугольной системе координат, соответствует общее уравнение: А1х+В1у+С1z+D1=0. А плоскость β определяется общим уравнением вида: А2х+В2у+С2z+D2=0.
Согласно теореме о параллельности плоскостей, чтобы α и β являлись параллельными, достаточно отсутствия решений системы линейных уравнений вида:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
То есть приведенная выше система должна быть несовместной.
Доказательство
Допустим, указанные плоскости, соответствующие уравнениям А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 параллельны друг другу, следовательно, у них отсутствуют общие точки. Это значит, что нет ни одной точки в прямоугольной системе координат, находящейся в трехмерном пространстве, чьи координаты отвечали бы условиям обоих уравнений одновременно или:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
не имеет решения.
В случае, если данная система уравнений не имеет решений, то в прямоугольной системе координат трехмерного пространства отсутствуют точки с координатами, одновременно отвечающими условиям обоих уравнений, входящих в рассматриваемую систему. Отсюда можно сделать вывод, что плоскости α и β с соответствующими им уравнениями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 не обладают ни одной общей точкой, а значит, являются параллельными. Теорема доказана.
Перпендикулярность
Две плоскости перпендикулярны друг другу, в ситуации, когда они при взаимном пересечении образуют прямой угол, то есть угол в 90°.
Теорема
Если одна из двух плоскостей проходит через прямую, которая перпендикулярна другой плоскости, то такие плоскости являются перпендикулярными.
Доказательство
Пусть: AB∈α, AB⊥β, AB∩β=A.
Необходимо доказать, что α⊥β.
- α∩β=AC, причем AB⊥AC по условию.
- Проведем прямую AD, принадлежащую плоскости β и перпендикулярную AC.
- ∠BAD=90°, поскольку AB⊥β. Следовательно, заданные плоскости перпендикулярны, что и требовалось доказать.
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две заданные плоскости, перпендикулярна к каждой из этих плоскостей.
Теорема
Явность перпендикулярных пересекающихся плоскостей достигается при необходимом и достаточном условии, что нормальные векторы данных плоскостей при пересечении образовали прямой угол.
Доказательство
Допустим, в трехмерном пространстве существует некоторая прямоугольная система координат. При наличии нормальных векторов заданных плоскостей α и β с координатами:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2),)
то необходимо и достаточно, чтобы эти векторы приняли вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Отсюда следует, что:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2))
— нормальные векторы плоскостей α и β. Чтобы заданные плоскости были перпендикулярными, достаточно, чтобы скалярное произведение данных векторов ровнялось нулю, то есть принимало вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Равенство соблюдено.
Угол между плоскостями
Для вычисления угла между двумя пересекающимися плоскостями используют метод координат. Суть данного способа заключается в нахождении косинуса угла, образованного при пересечении плоскостей.
Предположим, что плоскости P1 и P2 заданы следующими уравнениями:
(P_1:;A_1x+B_1y+C_1z+D_1=0,;{overline N}_1=left(A_1,B_1,C_1right);)
(P_2:;A_2x+B_2y+C_2z+D_2=0,;{overline N}_2=left(A_2,B_2,C_2right))
Найдем косинус угла между P1 и P2 по формуле:
(cosleft(overbrace{P_1,P_2}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}frac{A_1times A_2+B_1times B_2+C_1times C_2}{sqrt{A_1^2+B_1^2+C_1^2}timessqrt{A_2^2+B_2^2+C_2^2}})
Запишем в ответе модуль косинуса угла, поскольку за величину угла между плоскостями принимают острый угол.
Примеры решения задач
Задача №1
Плоскости заданы уравнениями:
(alpha:;x-y+1=0)
(beta:y-z+1=0)
Определить пересекаются ли α и β. В случае пересечения заданных плоскостей найти угол между ними.
Решение:
Найдем угол между заданными плоскостями:
(alpha:;x-y+1=0,Rightarrowoverline{N_1}=(1,-1,0);)
(beta:;y-z+1=0,Rightarrowoverline{N_2}=(0,1,-1))
Далее вычислим косинус угла между α и β:
(cosleft(overbrace{alpha,beta}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}=frac{1times0+left(-1right)times1+0timesleft(-1right)}{sqrt{1^2+left(-1right)^2+0^2}timessqrt{0^2+1^2+left(-1right)^2}}=frac{-1}{sqrt4}=-frac12)
В ответе запишем модуль найденной величины.
Ответ: плоскости α и β пересекаются, а косинус угла между ними равен ½.
Задача №2
Плоскость α проходит через точку A(1,1,−1) и перпендикулярна к плоскостям, заданным уравнениями:
(beta:;2x-y+5z+3=0;)
(varphi:;x+3y-z-7=0)
Составьте уравнение плоскости α.
Решение:
Необходимым и достаточным условием перпендикулярности α к плоскостям β и φ является параллельность α к нормалям β и φ — N1 и N2, иными словами, α должна быть перпендикулярна к произведению векторов [N1,N2].
(x = {-b pm sqrt{b^2-4ac} over 2a}beta:;2x-y+5z+3=0,Rightarrow;overline{N_1}=left(2,-1,5right))
(varphi:;x+3y-z-73=0,Rightarrow;overline{N_2}=left(1,3,-1right))
(left[N_1,N_2right]=begin{vmatrix}i&j&k\2&-1&5\1&3&-1end{vmatrix}=ileft(1-15right)-jleft(-2-5right)+kleft(6+1right)=-14i+7j+7k)
Следующим шагом выпишем уравнение плоскости α, проходящей через точку A(1,1,−1) и перпендикулярную вектору [N1,N2]=(−14,7,7):
(-14left(x-1right)+7left(y-1right)+7left(z+1right)=left.0right|:7)
(-2left(x-1right)+y-1+z+1=0)
(−2x+y+z+2=0)
Ответ: (−2x+y+z+2=0.)
Угол между плоскостями. Перпендикулярность плоскостей
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.
Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.
Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

Читаем дальше: Угол и расстояние между скрещивающимися прямыми.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Угол между плоскостями. Перпендикулярность плоскостей» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Статья рассказывает о нахождении угла между плоскостями. После приведения определения зададим графическую иллюстрацию, рассмотрим подробный способ нахождения методом координат. Получим формулу для пересекающихся плоскостей, в которую входят координаты нормальных векторов.
Угол между плоскостями – определение
В материале будут использованы данные и понятия, которые ранее были изучены в статьях про плоскость и прямую в пространстве. Для начала необходимо перейти к рассуждениям, позволяющим иметь определенный подход к определению угла между двумя пересекающимися плоскостями.
Заданы две пересекающиеся плоскости γ1 и γ2. Их пересечение примет обозначение c. Построение плоскости χ связано с пересечением этих плоскостей. Плоскость χ проходит через точку М в качестве прямой c. Будет производиться пересечение плоскостей γ1 и γ2 с помощью плоскости χ. Принимаем обозначения прямой, пересекающей γ1 и χ за прямую a, а пересекающую γ2 и χ за прямую b. Получаем, что пересечение прямых a и b дает точку M.
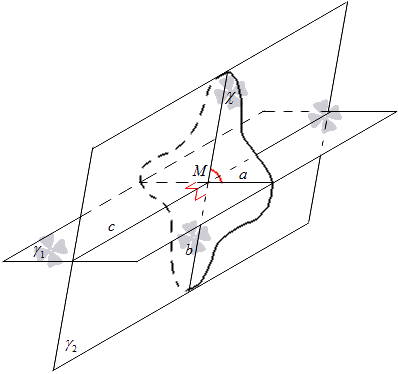
Расположение точки M не влияет на угол между пересекающимися прямыми a и b, а точка M располагается на прямой c, через которую проходит плоскость χ.
Необходимо построить плоскость χ1 с перпендикулярностью к прямой c и отличную от плоскости χ. Пересечение плоскостей γ1 и γ2 с помощью χ1 примет обозначение прямых а1 и b1.
Видно, что при построении χ и χ1 прямые a и b перпендикулярны прямой c, тогда и а1, b1 располагаются перпендикулярно прямой c. Нахождение прямых a и а1 в плоскости γ1 с перпендикулярностью к прямой c, тогда их можно считать параллельными. Таки же образом расположение b и b1 в плоскости γ2 с перпендикулярностью прямой c говорит об их параллельности. Значит, необходимо сделать параллельный перенос плоскости χ1 на χ, где получим две совпадающие прямые a и а1, b и b1. Получаем, что угол между пересекающимися прямыми a и b1 равен углу пересекающихся прямых a и b.
Рассмотрим не рисунке, приведенном ниже.
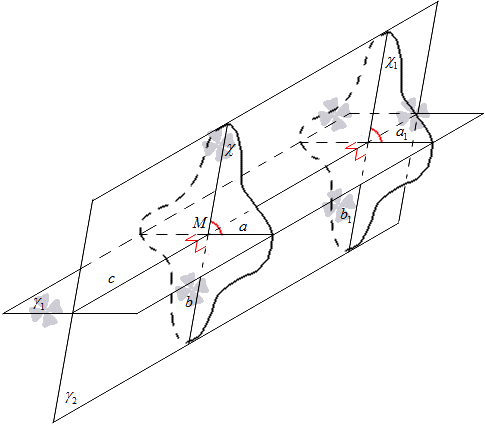
Данное суждение доказывается тем, что между пересекающимися прямыми a и b имеется угол, который не зависит от расположения точки M, то есть точки пересечения. Эти прямые располагаются в плоскостях γ1 и γ2. Фактически, получившийся угол можно считать углом между двумя пересекающимися плоскостями.
Перейдем к определению угла между имеющимися пересекающимися плоскостями γ1 и γ2.
Углом между двумя пересекающимися плоскостями γ1 и γ2 называют угол, образовавшийся путем пересечения прямых a и b, где плоскости γ1 и γ2 имеют пересечение с плоскостью χ, перпендикулярной прямой c.
Рассмотрим рисунок, приведенный ниже.
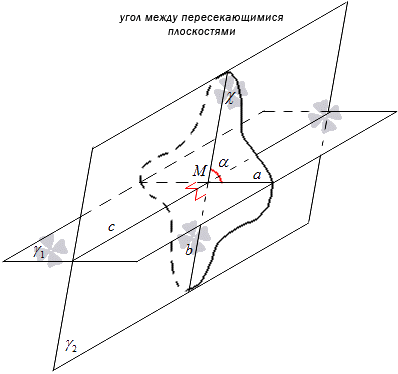
Определение может быть подано в другой форме. При пересечении плоскостей γ1 и γ2, где c – прямая, на которой они пересеклись, отметить точку M, через которую провести прямые a и b, перпендикулярные прямой c и лежащие в плоскостях γ1 и γ2, тогда угол между прямыми a и b будет являться углом между плоскостями. Практически это применимо для построения угла между плоскостями.
При пересечении образуется угол, который по значению меньше 90 градусов, то есть градусная мера угла действительна на промежутке такого вида (0, 90]. Одновременно данные плоскости называют перпендикулярными в случае, если при пересечении образуется прямой угол. Угол между параллельными плоскостями считается равным нулю.
Нахождение угла между двумя пересекающимися плоскостями
Обычный способ для нахождения угла между пересекающимися плоскостями – это выполнение дополнительных построений. Это способствует определять его с точностью, причем делать это можно с помощью признаков равенства или подобия треугольника, синусов, косинусов угла.
Рассмотрим решение задач на примере из задач ЕГЭ блока C2.
Задан прямоугольный параллелепипед АВСDA1B1C1D1, где сторона АВ=2, AD=3, АА1=7, точка E разделяет сторону АА1 в отношении 4:3. Найти угол между плоскостями АВС и ВED1.
Решение
Для наглядности необходимо выполнить чертеж. Получим, что
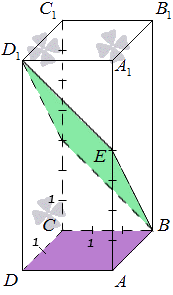
Наглядное представление необходимо для того, чтобы было удобней работать с углом между плоскостями.
Производим определение прямой линии, по которой происходит пересечение плоскостей АВС и ВED1. Точка B является общей точкой. Следует найти еще одну общую точку пересечения. Рассмотрим прямые DA и D1E, которые располагаются в одной плоскости ADD1. Их расположение не говорит о параллельности, значит, они имеют общую точку пересечения.
Однако, прямая DA расположена в плоскости АВС, а D1E в BED1. Отсюда получаем, что прямые DA и D1E имеют общую точку пересечения, которая является общей и для плоскостей АВС и BED1. Обозначает точку пересечения прямых DA и D1E буквой F. Отсюда получаем, что BF является прямой, по которой пересекаются плоскости АВС и ВED1.
Рассмотрим на рисунке, приведенном ниже.
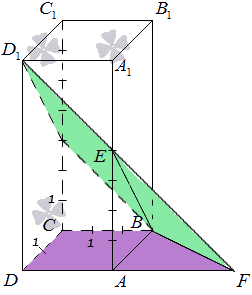
Для получения ответа необходимо произвести построение прямых, расположенных в плоскостях АВС и ВED1 с прохождением через точку, находящуюся на прямой BF и перпендикулярной ей. Тогда получившийся угол между этими прямыми считается искомым углом между плоскостями АВС и ВED1.
Отсюда видно, что точка A – проекция точки E на плоскость АВС. Необходимо провести прямую, пересекающую под прямым углом прямую BF в точке М. Видно, что прямая АМ – проекция прямой ЕМ на плоскость АВС, исходя из теоремы о тех перпендикулярах AM⊥BF. Рассмотрим рисунок, изображенный ниже.
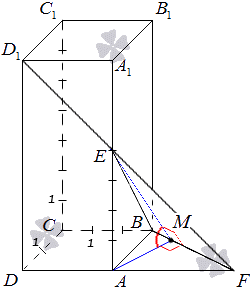
∠AME – это искомый угол, образованный плоскостями АВС и ВED1. Из получившегося треугольника АЕМ можем найти синус, косинус или тангенс угла, после чего и сам угол, только при известных двух сторонах его. По условию имеем, что длина АЕ находится таким образом: прямая АА1 разделена точкой E в отношении 4:3, то означает полную длину прямой – 7 частей, тогда АЕ= 4 частям. Находим АМ.
Необходимо рассмотреть прямоугольный треугольник АВF. Имеем прямой угол A с высотой АМ. Из условия АВ=2, тогда можем найти длину AF по подобию треугольников DD1F и AEF. Получаем, что AEDD1=AFDF⇔AEDD1=AFDA+AF⇒47=AF3+AF⇔AF=4
Необходимо найти длину стороны BF из треугольника ABF, используя теорему Пифагора. Получаем, что BF =AB2+AF2=22+42=25. Длина стороны АМ находится через площадь треугольника ABF. Имеем, что площадь может равняться как SABC=12·AB·AF, так и SABC=12·BF·AM.
Получаем, что AM=AB·AFBF=2·425=455
Тогда можем найти значение тангенса угла треугольника АЕМ. Получим:
tg∠AME=AEAM=4455=5
Искомый угол, получаемый пересечением плоскостей АВС и BED1 равняется arctg5, тогда при упрощении получим arctg5=arcsin 306=arccos66.
Ответ: arctg5=arcsin 306=arccos66.
Некоторые случаи нахождения угла между пересекающимися прямыми задаются при помощи координатной плоскости Охуz и методом координат. Рассмотрим подробней.
Если дана задача, где необходимо найти угол между пересекающимися плоскостями γ1 и γ2, искомый угол обозначим за α.
Тогда заданная система координат показывает, что имеем координаты нормальных векторов пересекающихся плоскостей γ1 и γ2. Тогда обозначим, что n1→=n1x, n1y, n1z является нормальным вектором плоскости γ1, а n2→=(n2x, n2y, n2z) – для плоскости γ2. Рассмотрим подробное нахождение угла, расположенного между этими плоскостями по координатам векторов.
Необходимо обозначить прямую, по которой происходит пересечение плоскостей γ1 и γ2 буквой c. На прямой с имеем точку M, через которую проводим плоскость χ, перпендикулярную c. Плоскость χ по прямым a и b производит пересечение плоскостей γ1 и γ2 в точке M. из определения следует, что угол между пересекающимися плоскостями γ1 и γ2 равен углу пересекающихся прямых a и b, принадлежащих этим плоскостям соответственно.
В плоскости χ откладываем от точки M нормальные векторы и обозначаем их n1→ и n2→. Вектор n1→ располагается на прямой, перпендикулярной прямой a, а вектор n2→ на прямой, перпендикулярной прямой b. Отсюда получаем, что заданная плоскость χ имеет нормальный вектор прямой a, равный n1→ и для прямой b, равный n2→. Рассмотрим рисунок, приведенный ниже.
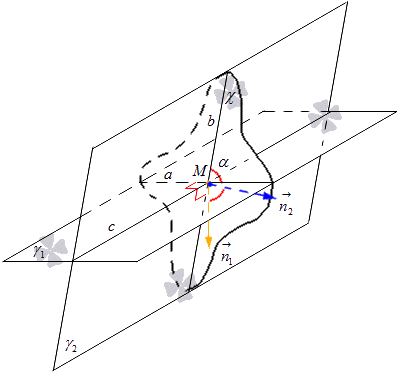
Отсюда получаем формулу, по которой можем вычислить синус угла пересекающихся прямых при помощи координат векторов. Получили, что косинусом угла между прямыми a и b то же, что и косинус между пересекающимися плоскостями γ1 и γ2 выводится из формулы cos α=cosn1→, n2→^=n1x·n2x+n1y·n2y+n1z·n2zn1x2+n1y2+n1z2·n2x2+n2y2+n2z2, где имеем, что n1→=(n1x, n1y, n1z) и n2→=(n2x, n2y, n2z) являются координатами векторов представленных плоскостей.
Вычисление угла между пересекающимися прямыми производится по формуле
α=arccosn1x·n2x+n1y·n2y+n1z·n2zn1x2+n1y2+n1z2·n2x2+n2y2+n2z2
По условию дан параллелепипед АВСDA1B1C1D1, где АВ=2, AD=3, АА1=7, а точка E разделяет сторону АА1 4:3. Найти угол между плоскостями АВС и BED1.
Решение
Из условия видно, что стороны его попарно перпендикулярны. Это значит, что необходимо ввести систему координат Охуz с вершиной в точке С и координатными осями Ох, Оу, Оz. Необходимо поставить направление по соответствующим сторонам. Рассмотрим рисунок, приведенный ниже.

Пересекающиеся плоскости АВС и BED1 образуют угол, который можно найти по формуле α=arccosn1x·n2x+n1y·n2y+n1z·n2zn1x2+n1y2+n1z2·n2x2+n2y2+n2z2 , в которой n1→=(n1x, n1y, n1z) и n2→=(n2x, n2y, n2z) являются нормальными векторами этих плоскостей. Необходимо определить координаты. По рисунку видим, что координатная ось Оху совпадает в плоскостью АВС, это значит, что координаты нормального вектора k→ равняются значению n1→=k→=(0, 0, 1).
За нормальный вектор плоскости BED1 принимается векторное произведение BE→ и BD1→, где их координаты находятся путем координат крайних точек В, Е, D1, которые определяются, исходя из условия задачи.
Получаем, что B (0, 3, 0), D1(2, 0, 7). Потому как AEEA1=43, из координат точек A2, 3, 0, A12, 3, 7 найдем E2, 3, 4. Получаем, что BE→=(2, 0, 4), BD1→=2, -3, 7n2→=BE→×BD1=i→j→k→2042-37=12·i→-6·j→-6·k→⇔n2→=(12, -6, -6)
Необходимо произвести подстановку найденных координат в формулу вычисления угла через арккосинус. Получаем
α=arccos0·12+0·(-6)+1·(-6)02+02+12·122+(-6)2+(-6)2=arccos 666=arccos 66
Метод координат дает аналогичный результат.
Ответ: arccos 66.
Завершающая задача рассматривается с целью нахождения угла между пересекающимися плоскостями при имеющихся известных уравнениях плоскостей.
Вычислить синус , косинус угла и значение угла, образованного двумя пересекающимися прямыми, которые определены в системе координат Охуz и заданы уравнениями 2x-4y+z+1=0 и 3y-z-1=0.
Решение
При изучении темы общего уравнения прямой вида Ax+By+Cz+D=0 выявили, что А, В, С являются коэффициентами, равными координатам нормального вектора. Значит, n1→=2, -4, 1 и n2→=0, 3, -1 являются нормальным векторами заданных прямых.
Необходимо подставить координаты нормальных векторов плоскостей в формулу вычисления искомого угла пересекающихся плоскостей. Тогда получаем, что
α=arccos2·0+-4·3+1·(-1)22+-42+12=arccos 13210
Отсюда имеем, что косинус угла принимает вид cos α=13210. Тогда угол пересекающихся прямых не является тупым. Подставив в тригонометрическое тождество, получаем, что значение синуса угла равняется выражению. Вычислим и получим, что
sin α=1-cos2 α=1-13210=41210
Ответ: sin α=41210, cos α=13210, α=arccos 13210=arcsin 41210.
