Калькулятор уклонов
- Главная
- /
- Строительство
- /
- Калькулятор уклонов
Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Посчитать уклон
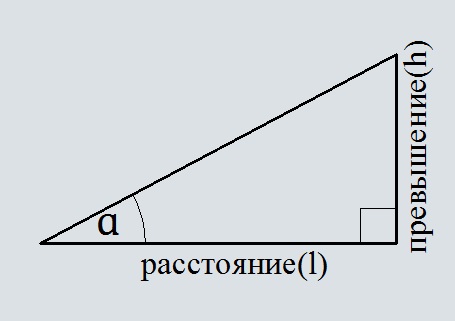
Расстояние L =
Превышение h =
Уклон α =
0
Посчитать превышение
Уклон α =
Расстояние L =
Превышение h =
0
Посчитать расстояние
Уклон α =
Превышение h =
Расстояние L =
0
Просто введите значения и выберите единицы измерения уклона.
Теория
Как посчитать уклон
Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:
В процентах:
Уклон в % = h / L ⋅ 100
В промилле:
Уклон в ‰ = h / L ⋅ 1000
В градусах:
Уклон в ° = arctg(h/L)
Пример
Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:
Уклон дороги = 30/500 ⋅ 100 = 6%
Как посчитать превышение
Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
h = L ⋅ Уклон в % /100
Если уклон в промилле (‰):
h = L ⋅ Уклон в ‰ /1000
Если уклон в градусах (°):
h = L ⋅ tg(α) , где α – уклон в градусах
Пример
Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:
h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м
Как посчитать расстояние
Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
L = h / Уклон в % ⋅ 100
Если уклон в промилле (‰):
L = h / Уклон в ‰ ⋅ 1000
Если уклон в градусах (°):
L = h / tg(α), где α – уклон в градусах
Пример
Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:
L = 6 / 30 ⋅1000 = 200 м
См. также
Углы наклона прямой
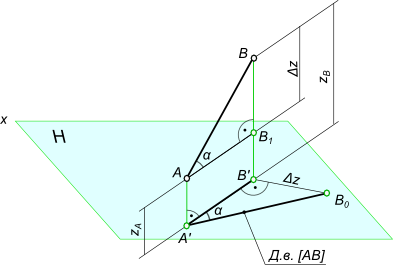
Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника.
В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
Углы наклона прямой
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).
Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
– первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
– из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
– гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
– угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.
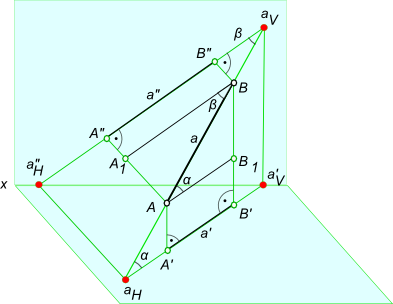
Углы наклона прямой
Для графического определения на эпюре Монжа действительной величины отрезка достаточно
построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную)
проекцию отрезка, а за другой катет – разность удаления концов отрезка от горизонтальной (или
соответственно фронтальной, профильной) плоскости проекции.
[
tg α = BB_1/AB_1 = (BB` – B`B_1)/AB_1 = (z_B – z_A)/A`B`
]
[
tg β = AA_1/BA_1 = (AA” – A”A_1)/BA_1 = (y_A – y_B)/A”B”
]
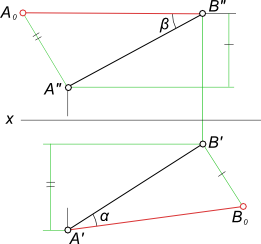
Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников
ΔA`B`B0 или ΔA”B”A0 и попутно углов его наклона:
– α к горизонтальной плоскости проекции;
– β к фронтальной плоскости проекции.
Углы наклона прямой
Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
– Горизонтальная прямая;
– Фронтальная прямая;
– Профильная прямая
Углы наклона прямой применяются в статье графическая работа 1: Графическая работа 1
Определение углов наклона плоскости смотри также: Линия наибольшего наклона
+
Расчёт уклона по расстоянию и превышению
Калькулятор рассчитывает уклон в градусах, процентах и промилле по известным превышению и расстоянию. С помощью него вы сумеете рассчитать угол наклона лестницы, процент уклона дороги, уклон трубопровода и.т.д.
Выберите что вы хотите найти
Введите расстояние l
Введите превышение h
Как рассчитать уклон
Для того чтобы рассчитать уклон необходимо знать расстояние и превышение.
Формула расчёта уклона в градусах через расстояние и превышение
Уклон в градусах ° = arctg(h/l)
Формула расчёта уклона в процентах через расстояние и превышение
Уклон в процентах % = h/l×100%
Формула расчёта уклона в промиле через расстояние и превышение
Уклон в промиле ‰ = h/l×1000‰
Похожие калькуляторы
По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?
Найдите правильный ответ на вопрос ✅ «По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде? …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Дано треугольник OBS угол B=90 градусов угол S=45 градусов OB=1008 СМ Найти SB
Ответы (1)
Дано abcd-параллелограмм, BCA=31 градусов, BAC=25 градусов
Ответы (1)
Один угол параллелограмма в 4 разОдин угол параллелограмма в 4 раза больше другого. Найдите больший угол. Ответ дайте в градусах. а больше другого. Найдите больший угол.
Ответы (1)
NK на 19 см. больше MN, MK = 81 см. Найти : MK, NK
Ответы (1)
Начертите угол AOB и лучи ОК и ОМ, проходящие между сторонами этого угла, так, чтобы угол AOB = 90, AOK = 40, MOB = 30, Найдите KOM
Ответы (1)
Главная » Геометрия » По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?
Разобравшись с выделением контуров объектов на видео, перейдем к более сложной задаче — обнаружению прямоугольников и эллипсов. Более того, мы не только научимся находить их в кадре, но еще и сможем определять угол их наклона!
Хорошим примером использования подобных алгоритмов может стать ситуация, когда роботу нужно правильно ухватиться за предмет. Прямо как на картинке.

Если смотреть на цилиндр сверху, то он превратится в прямоугольник. Зная его координаты в кадре и угол наклона можно рассчитать поворот схвата манипулятора, чтобы правильно ухватиться за предмет.
Сегодня на уроке:
- Функция OpenCV для поиска прямоугольников minAreaRect
- Функция OpenCV для поиска эллипсов fitEllipse
- Отсечение лишних контуров по площади
- Вычисление угла поворота прямоугольника в OpenCV
- Определение угла поворота прямоугольника в видеопотоке
1. Функция OpenCV для поиска прямоугольников minAreaRect
В OpenCV имеется функция, которая пытается найти прямоугольник максимального размера, который может вписаться в заданный замкнутый контур. Надо заметить, что эта функция не определяет является ли контур прямоугольным, она пытается вписать в него прямоугольник оптимальным способом. Это важно!
minAreaRect( контур )
контур — это контур, в который мы собираемся вписать прямоугольник (тип аргумента — Nx2 массив NumPy).
Напишем программу, которая найдет на картинке все прямоугольники. За основу возьмем код из предыдущего урока про поиск контуров.
#!/usr/bin/env python
import sys
import numpy as np
import cv2 as cv
hsv_min = np.array((0, 54, 5), np.uint8)
hsv_max = np.array((187, 255, 253), np.uint8)
if __name__ == '__main__':
fn = 'image2.jpg' # имя файла, который будем анализировать
img = cv.imread(fn)
hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV ) # меняем цветовую модель с BGR на HSV
thresh = cv.inRange( hsv, hsv_min, hsv_max ) # применяем цветовой фильтр
_, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
# перебираем все найденные контуры в цикле
for cnt in contours0:
rect = cv.minAreaRect(cnt) # пытаемся вписать прямоугольник
box = cv.boxPoints(rect) # поиск четырех вершин прямоугольника
box = np.int0(box) # округление координат
cv.drawContours(img,[box],0,(255,0,0),2) # рисуем прямоугольник
cv.imshow('contours', img) # вывод обработанного кадра в окно
cv.waitKey()
cv.destroyAllWindows()Результат работы программы:

Видно, что алгоритм попытался вписать прямоугольники во вложенные мусорные контуры на самих объектах. Далее мы разберемся как с этим бороться.
Теперь попробуем тоже самое, но с эллипсами.
2. Функция OpenCV для поиска эллипсов fitEllipse
Как и в случае minAreaRect, функция поиска эллипсов не сможет отличить на картинке объект с действительно эллиптическим контуром от квадрата. Она лишь пытается эллипс вписать в любой контур с количеством точек >=5.
fitEllipse( контур )
контур — это контур, в который мы собираемся вписать прямоугольник (тип аргумента — Nx2 массив NumPy).
Слегка изменим предыдущую программу, убрав из неё minAreaRect и добавив fitEllipse.
#!/usr/bin/env python
import sys
import numpy as np
import cv2 as cv
hsv_min = np.array((0, 77, 17), np.uint8)
hsv_max = np.array((208, 255, 255), np.uint8)
if __name__ == '__main__':
fn = 'donuts.jpg'
img = cv.imread(fn)
hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV )
thresh = cv.inRange( hsv, hsv_min, hsv_max )
_, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
for cnt in contours0:
if len(cnt)>4:
ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,0,255),2)
cv.imshow('contours', img)
cv.waitKey()
cv.destroyAllWindows()Условие
if len(cnt)>4:
необходимо для того, чтобы отсечь контуры с контурами меньше 5 точек. Результат работы программы:

Надо заметить, что эллипсы лучше пытаться вписать в округлые объекты, а прямоугольники в прямоугольные:) В противном случае, алгоритм может выдать неадекватные результаты.
3. Отсечение лишних контуров по площади
Следующий шаг — разберемся с паразитными микроконтурами, которые мы обнаружили на объектах. Избавиться от них можно, вычислив площадь занимаемую этими контурами, а затем просто отсечь контуры с маленькой площадью.
Внесем в нашу программу модификацию:
box = np.int0(box) # округление координат
area = int(rect[1][0]*rect[1][1]) # вычисление площади
if area > 500:
cv.drawContours(img,[box],0,(255,0,0),2)
Запускаем программу.

Наконец, вычислим углы наклона всех прямоугольников относительно горизонта. Здесь нам не понадобятся специальные функции OpenCV, достаточно будет простой математики.
#!/usr/bin/env python
import sys
import numpy as np
import cv2 as cv
import math
hsv_min = np.array((0, 54, 5), np.uint8)
hsv_max = np.array((187, 255, 253), np.uint8)
color_blue = (255,0,0)
color_yellow = (0,255,255)
if __name__ == '__main__':
fn = 'image2.jpg' # имя файла, который будем анализировать
img = cv.imread(fn)
hsv = cv.cvtColor( img, cv.COLOR_BGR2HSV ) # меняем цветовую модель с BGR на HSV
thresh = cv.inRange( hsv, hsv_min, hsv_max ) # применяем цветовой фильтр
_, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
# перебираем все найденные контуры в цикле
for cnt in contours0:
rect = cv.minAreaRect(cnt) # пытаемся вписать прямоугольник
box = cv.boxPoints(rect) # поиск четырех вершин прямоугольника
box = np.int0(box) # округление координат
center = (int(rect[0][0]),int(rect[0][1]))
area = int(rect[1][0]*rect[1][1]) # вычисление площади
# вычисление координат двух векторов, являющихся сторонам прямоугольника
edge1 = np.int0((box[1][0] - box[0][0],box[1][1] - box[0][1]))
edge2 = np.int0((box[2][0] - box[1][0], box[2][1] - box[1][1]))
# выясняем какой вектор больше
usedEdge = edge1
if cv.norm(edge2) > cv.norm(edge1):
usedEdge = edge2
reference = (1,0) # горизонтальный вектор, задающий горизонт
# вычисляем угол между самой длинной стороной прямоугольника и горизонтом
angle = 180.0/math.pi * math.acos((reference[0]*usedEdge[0] + reference[1]*usedEdge[1]) / (cv.norm(reference) *cv.norm(usedEdge)))
if area > 500:
cv.drawContours(img,[box],0,(255,0,0),2) # рисуем прямоугольник
cv.circle(img, center, 5, color_yellow, 2) # рисуем маленький кружок в центре прямоугольника
# выводим в кадр величину угла наклона
cv.putText(img, "%d" % int(angle), (center[0]+20, center[1]-20),
cv.FONT_HERSHEY_SIMPLEX, 1, color_yellow, 2)
cv.imshow('contours', img)
cv.waitKey()
cv.destroyAllWindows()Помним, что цветовые фильтры hsv_min и hsv_max нужно каждый раз настраивать под конкретный объект и освещение!
Запускаем программу, указав в ней в качестве исходного — изображение с макетными платами.

Ура! Работает. Ну и последний шаг — подключим видеопоток.
5. Определение угла поворота прямоугольника в видеопотоке
Здесь нам потребуется вспомнить урок про наложение текста и геометрических фигур на кадр в OpenCV.
#!/usr/bin/env python
import cv2 as cv
import numpy as np
import video
import math
if __name__ == '__main__':
cv.namedWindow( "result" )
cap = video.create_capture(0)
hsv_min = np.array((0, 0, 255), np.uint8)
hsv_max = np.array((72, 51, 255), np.uint8)
color_blue = (255,0,0)
color_red = (0,0,128)
while True:
flag, img = cap.read()
img = cv.flip(img,1)
try:
hsv = cv.cvtColor(img, cv.COLOR_BGR2HSV )
thresh = cv.inRange(hsv, hsv_min, hsv_max)
_, contours0, hierarchy = cv.findContours( thresh.copy(), cv.RETR_EXTERNAL, cv.CHAIN_APPROX_NONE)
for cnt in contours0:
rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
center = (int(rect[0][0]),int(rect[0][1]))
area = int(rect[1][0]*rect[1][1])
edge1 = np.int0((box[1][0] - box[0][0],box[1][1] - box[0][1]))
edge2 = np.int0((box[2][0] - box[1][0], box[2][1] - box[1][1]))
usedEdge = edge1
if cv.norm(edge2) > cv.norm(edge1):
usedEdge = edge2
reference = (1,0) # horizontal edge
angle = 180.0/math.pi * math.acos((reference[0]*usedEdge[0] + reference[1]*usedEdge[1]) / (cv.norm(reference) *cv.norm(usedEdge)))
if area > 500:
cv.drawContours(img,[box],0,color_blue,2)
cv.circle(img, center, 5, color_red, 2)
cv.putText(img, "%d" % int(angle), (center[0]+20, center[1]-20), cv.FONT_HERSHEY_SIMPLEX, 1, color_red, 2)
cv.imshow('result', img)
except:
cap.release()
raise
ch = cv.waitKey(5)
if ch == 27:
break
cap.release()
cv.destroyAllWindows()Помним про правильную настройку фильтров! Если всё сделано правильно, получится примерно это:
Your browser does not support the video tag.
К размышлению
Итак, хорошая новость — мы умеем определять угол наклона прямоугольника. Плохая новость — мы не можем быть уверены, что в кадре именно прямоугольник! Та же ситуация с эллипсом. Попробуем разобраться с более продвинутыми методами детектирования геометрических объектов на следующих уроках!
