
The angle of view is the decisive variable for the visual perception of the size or projection of the size of an object.
Angle of view and perception of size[edit]
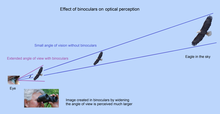
The perceived size of an object depends on the size of the image projected onto the retina. The size of the image depends on the angle of vision. A near and a far object can appear the same size if their edges produce the same angle of vision. With an optical device such as glasses or binoculars, microscope and telescope the angle of vision can be widened so that the object appears larger, which is favourable for the resolving power of the eye (see visual angle).[1][2]
Angle of view in photography[edit]
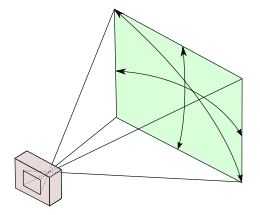
A camera’s angle of view can be measured horizontally, vertically, or diagonally.
In photography, angle of view (AOV)[3] describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term field of view.
It is important to distinguish the angle of view from the angle of coverage, which describes the angle range that a lens can image. Typically the image circle produced by a lens is large enough to cover the film or sensor completely, possibly including some vignetting toward the edge. If the angle of coverage of the lens does not fill the sensor, the image circle will be visible, typically with strong vignetting toward the edge, and the effective angle of view will be limited to the angle of coverage.

In 1916, Northey showed how to calculate the angle of view using ordinary carpenter’s tools.[4] The angle that he labels as the angle of view is the half-angle or “the angle that a straight line would take from the extreme outside of the field of view to the center of the lens;” he notes that manufacturers of lenses use twice this angle.

In this simulation, adjusting the angle of view and distance of the camera while keeping the object in frame results in vastly differing images. At distances approaching infinity, the light rays are nearly parallel to each other, resulting in a “flattened” image. At low distances and high angles of view objects appear “foreshortened”.
A camera’s angle of view depends not only on the lens, but also on the sensor. Digital sensors are usually smaller than 35 mm film, and this causes the lens to have a narrower angle of view than with 35 mm film, by a constant factor for each sensor (called the crop factor). In everyday digital cameras, the crop factor can range from around 1 (professional digital SLRs), to 1.6 (consumer SLR), to 2 (Micro Four Thirds ILC) to 6 (most compact cameras). So a standard 50 mm lens for 35 mm photography acts like a 50 mm standard “film” lens on a professional digital SLR, but would act closer to an 80 mm lens (1.6 x 50mm) on many mid-market DSLRs, and the 40 degree angle of view of a standard 50 mm lens on a film camera is equivalent to an 80 mm lens on many digital SLRs.
Calculating a camera’s angle of view[edit]
For lenses projecting rectilinear (non-spatially-distorted) images of distant objects, the effective focal length and the image format dimensions completely define the angle of view. Calculations for lenses producing non-rectilinear images are much more complex and in the end not very useful in most practical applications. (In the case of a lens with distortion, e.g., a fisheye lens, a longer lens with distortion can have a wider angle of view than a shorter lens with low distortion)[5]
Angle of view may be measured horizontally (from the left to right edge of the frame), vertically (from the top to bottom of the frame), or diagonally (from one corner of the frame to its opposite corner).
For a lens projecting a rectilinear image (focused at infinity, see derivation), the angle of view (α) can be calculated from the chosen dimension (d), and effective focal length (f) as follows:[6]



Because this is a trigonometric function, the angle of view does not vary quite linearly with the reciprocal of the focal length. However, except for wide-angle lenses, it is reasonable to approximate 

The effective focal length is nearly equal to the stated focal length of the lens (F), except in macro photography where the lens-to-object distance is comparable to the focal length. In this case, the magnification factor (m) must be taken into account:
(In photography 

Angle of view can also be determined using FOV tables or paper or software lens calculators.[7]

Log-log graphs of focal length vs crop factor vs diagonal, horizontal and vertical angles of view for film or sensors of 3:2 and 4:3 aspect ratios. The yellow line shows an example where 18 mm on 3:2 APS-C is equivalent to 27 mm and yields a vertical angle of 48 degrees.
Example[edit]
Consider a 50 mm camera with a lens having a focal length of F = 50 mm. The dimensions of the 35 mm image format are 24 mm (vertically) × 36 mm (horizontal), giving a diagonal of about 43.3 mm.
At infinity focus, f = F, the angles of view are:
- horizontally,
- vertically,
- diagonally,
Derivation of the angle-of-view formula[edit]
Consider a rectilinear lens in a camera used to photograph an object at a distance 


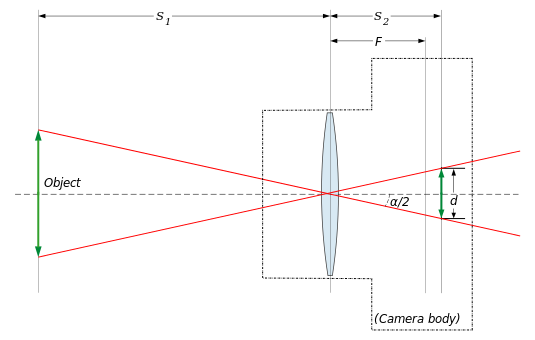
Now 

- the angle
- the “opposite” side of the right triangle,
(half the film-format dimension)
- the “adjacent” side,
(distance from the lens to the image plane)
Using basic trigonometry, we find:
which we can solve for α, giving:
To project a sharp image of distant objects, 

where 
Note that the angle of view varies slightly when the focus is not at infinity (See breathing (lens)), given by 
Macro photography[edit]
For macro photography, we cannot neglect the difference between 

From the definition of magnification, 

Defining 
where 
A second effect which comes into play in macro photography is lens asymmetry (an asymmetric lens is a lens where the aperture appears to have different dimensions when viewed from the front and from the back). The lens asymmetry causes an offset between the nodal plane and pupil positions. The effect can be quantified using the ratio (P) between apparent exit pupil diameter and entrance pupil diameter. The full formula for angle of view now becomes:[9]
Measuring a camera’s field of view[edit]
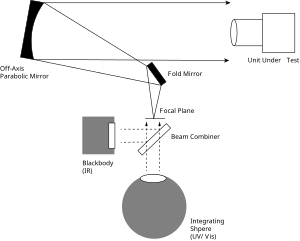
Schematic of collimator-based optical apparatus used in measuring the FOV of a camera.
In the optical instrumentation industry the term field of view (FOV) is most often used, though the measurements are still expressed as angles.[10] Optical tests are commonly used for measuring the FOV of UV, visible, and infrared (wavelengths about 0.1–20 μm in the electromagnetic spectrum) sensors and cameras.
The purpose of this test is to measure the horizontal and vertical FOV of a lens and sensor used in an imaging system, when the lens focal length or sensor size is not known (that is, when the calculation above is not immediately applicable). Although this is one typical method that the optics industry uses to measure the FOV, there exist many other possible methods.
UV/visible light from an integrating sphere (and/or other source such as a black body) is focused onto a square test target at the focal plane of a collimator (the mirrors in the diagram), such that a virtual image of the test target will be seen infinitely far away by the camera under test. The camera under test senses a real image of the virtual image of the target, and the sensed image is displayed on a monitor.[11]

Monitor display of sensed image from the camera under test
The sensed image, which includes the target, is displayed on a monitor, where it can be measured. Dimensions of the full image display and of the portion of the image that is the target are determined by inspection (measurements are typically in pixels, but can just as well be inches or cm).
= dimension of full image
= dimension of image of target
The collimator’s distant virtual image of the target subtends a certain angle, referred to as the angular extent of the target, that depends on the collimator focal length and the target size. Assuming the sensed image includes the whole target, the angle seen by the camera, its FOV, is this angular extent of the target times the ratio of full image size to target image size.[12]
The target’s angular extent is:
where 

The total field of view is then approximately:
or more precisely, if the imaging system is rectilinear:
This calculation could be a horizontal or a vertical FOV, depending on how the target and image are measured.
Lens types and effects[edit]
Focal length[edit]

How focal length affects perspective: Varying focal lengths at identical field size achieved by different camera-subject distances. Notice that the shorter the focal length and the larger the angle of view, perspective distortion and size differences increase.
Lenses are often referred to by terms that express their angle of view:
- Fisheye lenses, typical focal lengths are between 8 mm and 10 mm for circular images, and 15–16 mm for full-frame images. Up to 180° and beyond.
- A circular fisheye lens (as opposed to a full-frame fisheye) is an example of a lens where the angle of coverage is less than the angle of view. The image projected onto the film is circular because the diameter of the image projected is narrower than that needed to cover the widest portion of the film.
- Ultra wide angle lens is a rectilinear which is less than 24 mm of focal length in 35 mm film format, here 14 mm gives 114° and 24 mm gives 84° .
- Wide-angle lenses (24–35 mm in 35 mm film format) cover between 84° and 64°
- Normal, or Standard lenses (36–60 mm in 35 mm film format) cover between 62° and 40°
- Long focus lenses (any lens with a focal length greater than the diagonal of the film or sensor used)[13] generally have an angle of view of 35° or less.[14] Since photographers usually only encounter the telephoto lens sub-type,[15] they are referred to in common photographic parlance as:
- “Medium telephoto”, a focal length of 85 mm to 250 mm in 35 mm film format covering between 30° and 10°[16]
- “Super telephoto” (over 300 mm in 35 mm film format) generally cover between 8° through less than 1°[16]
Zoom lenses are a special case wherein the focal length, and hence angle of view, of the lens can be altered mechanically without removing the lens from the camera.
Characteristics[edit]
For a given camera–subject distance, longer lenses magnify the subject more. For a given subject magnification (and thus different camera–subject distances), longer lenses appear to compress distance; wider lenses appear to expand the distance between objects.
Another result of using a wide angle lens is a greater apparent perspective distortion when the camera is not aligned perpendicularly to the subject: parallel lines converge at the same rate as with a normal lens, but converge more due to the wider total field. For example, buildings appear to be falling backwards much more severely when the camera is pointed upward from ground level than they would if photographed with a normal lens at the same distance from the subject, because more of the subject building is visible in the wide-angle shot.
Because different lenses generally require a different camera–subject distance to preserve the size of a subject, changing the angle of view can indirectly distort perspective, changing the apparent relative size of the subject and foreground.
If the subject image size remains the same, then at any given aperture all lenses, wide angle and long lenses, will give the same depth of field.[17]
Examples[edit]
An example of how lens choice affects angle of view.
|
28 mm lens, 65.5° × 46.4° |
50 mm lens, 39.6° × 27.0° |
|
70 mm lens, 28.9° × 19.5° |
210 mm lens, 9.8° × 6.5° |
Common lens angles of view[edit]
This table shows the diagonal, horizontal, and vertical angles of view, in degrees, for lenses producing rectilinear images, when used with 36 mm × 24 mm format (that is, 135 film or full-frame 35 mm digital using width 36 mm, height 24 mm, and diagonal 43.3 mm for d in the formula above).[18] Digital compact cameras sometimes state the focal lengths of their lenses in 35 mm equivalents, which can be used in this table.
For comparison, the human visual system perceives an angle of view of about 140° by 80°.[19]
| Focal length (mm) | Diagonal (°) | Vertical (°) | Horizontal (°) |
|---|---|---|---|
| 0 | 180.0 | 180.0 | 180.0 |
| 2 | 169.4 | 161.1 | 166.9 |
| 12 | 122.0 | 90.0 | 111.1 |
| 14 | 114.2 | 81.2 | 102.7 |
| 16 | 107.1 | 73.9 | 95.1 |
| 20 | 94.5 | 61.9 | 82.4 |
| 24 | 84.1 | 53.1 | 73.7 |
| 35 | 63.4 | 37.8 | 54.4 |
| 50 | 46.8 | 27.0 | 39.6 |
| 70 | 34.4 | 19.5 | 28.8 |
| 85 | 28.6 | 16.1 | 23.9 |
| 105 | 23.3 | 13.0 | 19.5 |
| 200 | 12.3 | 6.87 | 10.3 |
| 300 | 8.25 | 4.58 | 6.87 |
| 400 | 6.19 | 3.44 | 5.15 |
| 500 | 4.96 | 2.75 | 4.12 |
| 600 | 4.13 | 2.29 | 3.44 |
| 700 | 3.54 | 1.96 | 2.95 |
| 800 | 3.10 | 1.72 | 2.58 |
| 1200 | 2.07 | 1.15 | 1.72 |

Five images using 24, 28, 35, 50 and 72 mm equivalent zoom lengths, portrait format, to illustrate angles of view[20]

Five images using 24, 28, 35, 50 and 72 mm equivalent step zoom function, to illustrate angles of view
Sensor size effects (“crop factor”)[edit]
As noted above, a camera’s angle level of view depends not only on the lens, but also on the sensor used. Digital sensors are usually smaller than 35 mm film, causing the lens to usually behave as a longer focal length lens would behave, and have a narrower angle of view than with 35 mm film, by a constant factor for each sensor (called the crop factor). In everyday digital cameras, the crop factor can range from around 1 (professional digital SLRs), to 1.6 (mid-market SLRs), to around 3 to 6 for compact cameras. So a standard 50 mm lens for 35 mm photography acts like a 50 mm standard “film” lens even on a professional digital SLR, but would act closer to a 75mm (1.5×50 mm Nikon) or 80mm lens (1.6×50 mm Canon) on many mid-market DSLRs, and the 40 degree angle of view of a standard 50mm lens on a film camera is equivalent to a 28–35 mm lens on many digital SLRs.
The table below shows the horizontal, vertical and diagonal angles of view, in degrees, when used with 22.2 mm × 14.8 mm format (that is Canon’s DSLR APS-C frame size) and a diagonal of 26.7 mm.
| Focal length (mm) | Diagonal (°) | Vertical (°) | Horizontal (°) |
|---|---|---|---|
| 2 | 162.9 | 149.8 | 159.6 |
| 4 | 146.6 | 123.2 | 140.4 |
| 7 | 124.6 | 93.2 | 115.5 |
| 9 | 112.0 | 78.9 | 101.9 |
| 12 | 96.1 | 63.3 | 85.5 |
| 14 | 87.2 | 55.7 | 76.8 |
| 16 | 79.6 | 49.6 | 69.5 |
| 17 | 76.2 | 47.0 | 66.3 |
| 18 | 73.1 | 44.7 | 63.3 |
| 20 | 67.4 | 40.6 | 58.1 |
| 24 | 58.1 | 34.3 | 49.6 |
| 35 | 41.7 | 23.9 | 35.2 |
| 50 | 29.9 | 16.8 | 25.0 |
| 70 | 21.6 | 12.1 | 18.0 |
| 85 | 17.8 | 10.0 | 14.9 |
| 105 | 14.5 | 8.1 | 12.1 |
| 200 | 7.6 | 4.2 | 6.4 |
| 210 | 7.3 | 4.0 | 6.1 |
| 300 | 5.1 | 2.8 | 4.2 |
| 400 | 3.8 | 2.1 | 3.2 |
| 500 | 3.1 | 1.7 | 2.5 |
| 600 | 2.5 | 1.4 | 2.1 |
| 700 | 2.2 | 1.2 | 1.8 |
| 800 | 1.9 | 1.1 | 1.6 |
Cinematography and video gaming[edit]
| Ratio | 1080p resolution | Common name | Video format / lens |
|---|---|---|---|
| 32:27 | 1280x1080p | DVCPRO HD | |
| 4:3 | 1440x1080p | ||
| 16:9 | 1920x1080p | Widescreen | |
| 2:1 | 2160×1080 | 18:9 | Univisium |
| 64:27 | 2560x1080p | Ultra-Widescreen | Cinemascope / Anamorphic |
| 32:9 | 3840x1080p | Super Ultra-Widescreen | Ultra-Widescreen 3.6 / Anamorphic 3.6 |
Modifying the angle of view over time (known as zooming), is a frequently used cinematic technique, often combined with camera movement to produce a “dolly zoom” effect, made famous by the film Vertigo. Using a wide angle of view can exaggerate the camera’s perceived speed, and is a common technique in tracking shots, phantom rides, and racing video games. See also Field of view in video games.
See also[edit]
- 35 mm equivalent focal length
- Camera angle
- Camera coverage
- Camera operator
- Cinematic techniques
- Field of view
- Filmmaking
- Multiple-camera setup
- Single-camera setup
- Video production
- Image sensor format
- Crop factor
- Ultrawide formats
Notes and references[edit]
- ^ Light microscopy online theory and application – Optics page 24
- ^ Georg Eisner: Perspektive und Visuelles System page 134
- ^ Tim Dobbert (November 2012). Matchmoving: The Invisible Art of Camera Tracking, 2nd Edition. John Wiley & Sons. p. 116. ISBN 9781118529669.
- ^ Neil Wayne Northey (September 1916). Frank V. Chambers (ed.). “The Angle of View of your Lens”. The Camera. Columbia Photographic Society. 20 (9).
- ^ “Canon EF 15mm f/2.8 Fisheye Lens Review”. The-Digital-Picture.com. Archived from the original on 7 August 2017. Retrieved 1 May 2018.
- ^ Ernest McCollough (1893). “Photographic Topography”. Industry: A Monthly Magazine Devoted to Science, Engineering and Mechanic Arts. Industrial Publishing Company, San Francisco: 399–406.
- ^ CCTV Field of View Camera Lens Calculations Archived 2008-08-22 at the Wayback Machine by JVSG, December, 2007
- ^ Kerr, Douglas A. (2008). “The Proper Pivot Point for Panoramic Photography” (PDF). The Pumpkin. Retrieved 2014-03-20.
- ^ Paul van Walree (2009). “Center of perspective”. Archived from the original on 30 April 2009. Retrieved 24 January 2010.
- ^ Holst, G.C. (1998). Testing and Evaluation of Infrared Imaging Systems (2nd ed.). Florida:JCD Publishing, Washington:SPIE.
- ^ Mazzetta, J.A.; Scopatz, S.D. (2007). Automated Testing of Ultraviolet, Visible, and Infrared Sensors Using Shared Optics. Infrared Imaging Systems: Design Analysis, Modeling, and Testing XVIII,Vol. 6543, pp. 654313-1 654313-14
- ^ Electro Optical Industries, Inc.(2005). EO TestLab Methadology. In Education/Ref. “Education and Reference”. Archived from the original on 2008-08-28. Retrieved 2008-05-22..
- ^ Ray, Sidney F. (1 May 2018). Applied Photographic Optics: Lenses and Optical Systems for Photography, Film, Video, Electronic and Digital Imaging. Focal. ISBN 9780240515403. Retrieved 1 May 2018 – via Google Books.
- ^ Lynne Warren, Encyclopedia of 20th century photography, page 211
- ^ Langford, Michael (1 May 2018). Basic Photography. Focal Press. ISBN 9780240515922. Retrieved 1 May 2018 – via Google Books.
- ^ a b “Your Site”. www.photographywebsite.co.uk. Retrieved 1 May 2018.
- ^ Reichmann, Michael. “Do Wide Angle Lenses Really Have Greater Depth of Field Than Telephotos?”. Archived from the original on 2011-06-10. Retrieved 2011-07-08.
- ^ However, most interchangeable-lens digital cameras do not use 24×36 mm image sensors and therefore produce narrower angles of view than set out in the table. See crop factor and the subtopic digital camera issues in the article on wide-angle lenses for further discussion.
- ^ Kollin, Joel S. (1993). A Retinal Display for Virtual-Environment Applications. Proceedings of Society for Information Display. Vol. XXIV. p. 827. Archived from the original on 2013-07-04. Retrieved 2014-04-27.
- ^ The image examples uses a 5.1–15.3 mm lens which is called a 24 mm 3× zoom by the producer (Ricoh Caplio GX100 Archived 2009-06-01 at the Wayback Machine)
External links[edit]
- Simple Explanation of Angle of View and Focal Length
- Angle of View on digital SLR cameras with reduced sensor size
- Focal Length and Angle of View

Камеры угол обзора можно измерять по горизонтали, вертикали или диагонали.
В фотография, угол обзора (AOV)[1] описывает угловатый протяженность данной сцены, отображаемой камера. Он используется взаимозаменяемо с более общим термином поле зрения.
Важно отличать угол обзора от угол обзора, который описывает диапазон углов, который может отображать объектив. Обычно круг изображения производимый линзой, достаточно большой, чтобы полностью покрыть пленку или датчик, возможно, включая некоторые виньетирование к краю. Если угол обзора объектива не заполняет датчик, круг изображения будет виден, обычно с сильным виньетированием по направлению к краю, а эффективный угол обзора будет ограничен углом покрытия.

В 1916 году Норти показал, как рассчитать угол обзора с помощью обычных плотницких инструментов.[2] Угол, который он называет углом зрения, – это половинный угол или «угол, который прямая линия принимает от крайнего края поля зрения к центру линзы»; он отмечает, что производители линз используют вдвое больший угол.

В этом моделировании регулировка угла обзора и расстояния до камеры при сохранении объекта в кадре приводит к сильно различающимся изображениям. На расстояниях, приближающихся к бесконечности, лучи света почти параллельны друг другу, что приводит к «сплющенному» изображению. На малых расстояниях и больших углах обзора объекты кажутся «укороченными».
Угол обзора камеры зависит не только от объектива, но и от сенсора. Цифровые датчики обычно меньше 35 мм пленка, и это приводит к тому, что объектив имеет более узкий угол обзора, чем у 35-мм пленки, за счет постоянного коэффициента для каждого датчика (называемого фактор урожая ). В обычных цифровых фотоаппаратах кроп-фактор может варьироваться от 1 (профессиональные цифровые SLR ), до 1,6 (бытовые SLR), до 2 (Микро 4/3 ILC) до 6 (большинство компактные камеры ). Таким образом, стандартный 50-миллиметровый объектив для 35-миллиметровой фотографии действует как стандартный 50-миллиметровый «пленочный» объектив на профессиональных цифровых SLR, но будет действовать ближе к 80-миллиметровому объективу (1,6 x 50 мм) на многих цифровых зеркальных фотокамерах среднего размера, а 40 градусный угол зрения стандартного объектива 50 мм на пленочной камере эквивалентен объективу 80 мм на многих цифровых SLR.
Расчет угла обзора камеры
Для проецирования линз прямолинейный (пространственно-неискаженные) изображения удаленных объектов, эффективное фокусное расстояние а размеры формата изображения полностью определяют угол обзора. Расчеты для линз, создающих непрямолинейные изображения, намного сложнее и, в конце концов, не очень полезны в большинстве практических приложений. (В случае объектива с искажением, например, объектив рыбий глаз, более длинный объектив с искажениями может иметь более широкий угол обзора, чем более короткий объектив с низким искажением)[3]Угол обзора может быть измерен по горизонтали (от левого к правому краю кадра), по вертикали (от верха до низа кадра) или по диагонали (от одного угла кадра к противоположному углу).
Для объектива, проецирующего прямолинейное изображение (сфокусированное на бесконечность, см. происхождение ), угол обзора (α) можно рассчитать исходя из выбранного размера (d) и эффективное фокусное расстояние (ж) следующим образом:[4]



Поскольку это тригонометрическая функция, угол обзора не изменяется линейно с обратной величиной фокусного расстояния. Однако, за исключением широкоугольных объективов, разумно приблизить 

Эффективное фокусное расстояние почти равно заявленному фокусному расстоянию объектива (F), кроме макросъемка где расстояние от линзы до объекта сравнимо с фокусным расстоянием. В этом случае увеличение фактор (м) необходимо учитывать:
(В фотографии 

Угол обзора также можно определить с помощью таблиц FOV, бумажных или программных калькуляторов линз.[5]

Логарифмические графики зависимости фокусного расстояния от кроп-фактора от диагонального, горизонтального и вертикального углов обзора для пленки или датчиков с соотношением сторон 3: 2 и 4: 3. Желтая линия показывает пример, где 18 мм для 3: 2 APS-C эквивалентно 27 мм и дает вертикальный угол 48 градусов.
пример
Рассмотрим камеру 50 мм с объективом с фокусным расстоянием F = 50 мм. Размеры изображения формата 35 мм составляют 24 мм (по вертикали) × 36 мм (по горизонтали), что дает диагональ около 43,3 мм.
В фокусе бесконечности, ж = F, углы обзора составляют:
- по горизонтали,
- вертикально,
- по диагонали,
Вывод формулы угла зрения
Рассмотрим прямолинейный объектив в фотоаппарате, который используется для фотографирования объекта на расстоянии. 



Сейчас же 

-
- угол
- “противоположная” сторона прямоугольного треугольника,
(половина размера пленки)
- “смежная” сторона,
(расстояние от линзы до плоскости изображения)
- угол
Используя базовую тригонометрию, мы находим:
который мы можем решить для α, давая:
Чтобы проецировать четкое изображение удаленных объектов, 

-
где
Обратите внимание, что угол обзора немного меняется, когда фокус не на бесконечности (см. дыхание (линза) ), заданный 
Макро фотография
В макросъемке нельзя пренебрегать разницей между 

-
.
Из определения увеличение, 

Определение 
-
где
.
Второй эффект, который проявляется в макросъемке, – это асимметрия объектива (асимметричный объектив – это объектив, в котором диафрагма имеет разные размеры при просмотре спереди и сзади). Асимметрия линзы вызывает смещение между узловой плоскостью и положением зрачка. Эффект можно количественно оценить с помощью отношения (п) между кажущимся диаметром выходного зрачка и диаметром входного зрачка. Полная формула угла обзора теперь выглядит следующим образом:[7]
Измерение поля зрения камеры

Схема коллиматор оптическая аппаратура, используемая для измерения поля обзора камеры.
В индустрии оптических приборов термин поле зрения (FOV) чаще всего используется, хотя измерения по-прежнему выражаются в углах.[8] Оптические тесты обычно используются для измерения поля зрения УФ, видимый, и инфракрасный (длины волн около 0,1–20 мкм в электромагнитный спектр ) датчики и камеры.
Целью этого теста является измерение горизонтального и вертикального поля зрения объектива и датчика, используемых в системе формирования изображения, когда фокусное расстояние объектива или размер датчика неизвестны (то есть, когда приведенный выше расчет не применим сразу). Хотя это один из типичных методов, оптика промышленность использует для измерения поля зрения, существует много других возможных методов.
УФ / видимый свет от интегрирующая сфера (и / или другой источник, такой как черное тело ) сфокусирован на квадратной тестовой мишени на фокальная плоскость из коллиматор (зеркала на диаграмме), так что виртуальное изображение тестовой цели будет бесконечно удалено тестируемой камерой. Тестируемая камера воспринимает реальное изображение виртуального изображения цели, и полученное изображение отображается на мониторе.[9]

Отображение на мониторе воспринимаемого изображения с тестируемой камеры
Обнаруженное изображение, включающее цель, отображается на мониторе, где его можно измерить. Размеры отображения полного изображения и части изображения, которая является целью, определяются путем осмотра (измерения обычно производятся в пикселях, но также могут быть дюймы или см).
-
= размер полного изображения
= размер изображения цели
Удаленное виртуальное изображение цели коллиматора имеет определенный угол, называемый угловой протяженностью цели, который зависит от фокусного расстояния коллиматора и размера цели. Предполагая, что воспринимаемое изображение включает в себя всю цель, угол обзора камеры, ее FOV, равен этой угловой протяженности цели, умноженной на отношение полного размера изображения к размеру целевого изображения.[10]
Угловая протяженность цели составляет:
-
- где
размер цели и
– фокусное расстояние коллиматора.
- где
Полное поле зрения тогда приблизительно:
или, точнее, если система визуализации прямолинейный:
Этот расчет может быть горизонтальным или вертикальным полем обзора, в зависимости от того, как измеряются цель и изображение.
Типы линз и эффекты
Фокусное расстояние

Как фокусное расстояние влияет на перспективу: разные фокусные расстояния при одинаковых размер поля достигается за счет различного расстояния между камерой и объектом. Обратите внимание, что чем короче фокусное расстояние и тем больше угол обзора, перспективное искажение и разница в размерах увеличивается.
Для обозначения линз часто используются термины, выражающие их угол зрения:
- Линзы рыбий глаз, типичные фокусные расстояния составляют от 8 мм до 10 мм для круглых изображений и 15–16 мм для полнокадровых изображений. До 180 ° и выше.
- А круглая линза рыбий глаз (в отличие от полнокадрового «рыбьего глаза») – это пример объектива, у которого угол покрытия меньше угла обзора. Изображение, проецируемое на пленку, является круглым, потому что диаметр проецируемого изображения равен уже чем это необходимо для покрытия самой широкой части пленки.
- Сверхширокоугольный объектив это прямолинейный что меньше 24 мм фокусное расстояние в формате пленки 35 мм, здесь 14 мм дают 114 °, а 24 мм дают 84 °.
- Широкоугольные объективы (24–35 мм в формате пленки 35 мм) охват от 84 ° до 64 °
- Нормальные или стандартные линзы (36–60 мм в формате пленки 35 мм) охват от 62 ° до 40 °
- Линзы с длинным фокусом (любой объектив с фокусным расстоянием больше, чем диагональ используемой пленки или сенсора)[11] обычно имеют угол обзора 35 ° или меньше.[12] Поскольку фотографы обычно сталкиваются только с телеобъектив подтип,[13] они называются в обычном фотографическом языке как:
- «Средний телефото», фокусное расстояние от 85 мм до 250 мм в формате пленки 35 мм, охват от 30 ° до 10 °[14]
- «Супертелеобъектив» (более 300 мм в формате пленки 35 мм) обычно охватывает от 8 ° до менее 1 °[14]
Зум-объективы представляют собой особый случай, когда фокусное расстояние и, следовательно, угол обзора объектива можно изменять механически, не снимая объектив с камеры.
Характеристики
При заданном расстоянии между камерой и объектом более длинные линзы увеличивают объект в большей степени. Для данного увеличения объекта (и, следовательно, различного расстояния между камерой и объектом) кажется, что более длинные линзы сжимают расстояние; кажется, что более широкие линзы увеличивают расстояние между объектами.
Еще один результат использования широкоугольного объектива – более очевидный перспективное искажение когда камера не ориентирована перпендикулярно объекту: параллельные линии сходятся с той же скоростью, что и нормальный объектив, но больше сходятся из-за более широкого общего поля. Например, кажется, что здания падают назад гораздо сильнее, когда камера направлена вверх от уровня земли, чем при съемке с обычным объективом на том же расстоянии от объекта, потому что большая часть здания объекта видна в широком диапазоне. Угловой выстрел.
Поскольку для разных объективов обычно требуется разное расстояние между камерой и объектом, чтобы сохранить размер объекта, изменение угла обзора может косвенно искажать перспектива, изменяя видимый относительный размер объекта и переднего плана.
Если размер изображения объекта остается прежним, то при любой заданной диафрагме все объективы, широкоугольные и длинные линзы будут давать одинаковые глубина резкости.[15]
Примеры
Пример того, как выбор объектива влияет на угол обзора.
|
Объектив 28 мм, 65,5 ° × 46,4 ° |
Объектив 50 мм, 39,6 ° × 27,0 ° |
|
Объектив 70 мм, 28,9 ° × 19,5 ° |
Объектив 210 мм, 9,8 ° × 6,5 ° |
Общие углы обзора линз
В этой таблице показаны диагональный, горизонтальный и вертикальный углы обзора в градусах для линз, создающих прямолинейные изображения, при использовании формата 36 мм × 24 мм (т. Е. 135 фильм или полнокадровый 35 мм цифровой используя ширину 36 мм, высоту 24 мм и диагональ 43,3 мм для d в формуле выше).[16] Цифровые компактные камеры иногда указывают фокусные расстояния своих объективов в эквиваленте 35 мм, которые можно использовать в этой таблице.
Для сравнения: зрительная система человека воспринимает угол зрения примерно 140 на 80 °.[17]
| Фокусное расстояние (мм) | Диагональ (°) | Вертикальный (°) | По горизонтали (°) |
|---|---|---|---|
| 0 | 180.0 | 180.0 | 180.0 |
| 2 | 169.4 | 161.1 | 166.9 |
| 12 | 122.0 | 90.0 | 111.1 |
| 14 | 114.2 | 81.2 | 102.7 |
| 16 | 107.1 | 73.9 | 95.1 |
| 20 | 94.5 | 61.9 | 82.4 |
| 24 | 84.1 | 53.1 | 73.7 |
| 35 | 63.4 | 37.8 | 54.4 |
| 50 | 46.8 | 27.0 | 39.6 |
| 70 | 34.4 | 19.5 | 28.8 |
| 85 | 28.6 | 16.1 | 23.9 |
| 105 | 23.3 | 13.0 | 19.5 |
| 200 | 12.3 | 6.87 | 10.3 |
| 300 | 8.25 | 4.58 | 6.87 |
| 400 | 6.19 | 3.44 | 5.15 |
| 500 | 4.96 | 2.75 | 4.12 |
| 600 | 4.13 | 2.29 | 3.44 |
| 700 | 3.54 | 1.96 | 2.95 |
| 800 | 3.10 | 1.72 | 2.58 |
| 1200 | 2.07 | 1.15 | 1.72 |

Пять изображений с эквивалентными длинами увеличения 24, 28, 35, 50 и 72 мм, портретный формат, для иллюстрации углов обзора [18]

Пять изображений с эквивалентной функцией ступенчатого масштабирования 24, 28, 35, 50 и 72 мм для иллюстрации углов обзора
Влияние размера сенсора (“кроп-фактор”)
Как отмечалось выше, угол обзора камеры зависит не только от объектива, но и от используемого датчика. Цифровые датчики обычно меньше 35-мм пленки, из-за чего объектив обычно ведет себя так же, как и объектив с большим фокусным расстоянием, и имеет более узкий угол обзора, чем 35-мм пленка, с постоянным коэффициентом для каждого датчика (называемым фактор урожая ). В обычных цифровых фотоаппаратах кроп-фактор может варьироваться от 1 (профессиональные цифровые SLR ), до 1,6 (SLR среднего размера), примерно до 3–6 для компактные камеры. Так что стандартный объектив 50 мм для Фотография 35 мм действует как стандартный «пленочный» объектив 50 мм даже на профессиональных цифровых зеркальных фотокамерах, но действует ближе к 75 мм (1,5 × 50 мм Nikon) или 80 мм (1,6 × 50 мм Canon) на многих цифровых зеркальных фотокамерах среднего размера, а Стандартный 50-миллиметровый объектив пленочной камеры с углом обзора 40 градусов эквивалентен 28–35-миллиметровому объективу на многих цифровых SLR.
В таблице ниже показаны горизонтальный, вертикальный и диагональный углы обзора в градусах при использовании формата 22,2 × 14,8 мм (т.е. Размер кадра DSLR APS-C ) и диагональю 26,7 мм.
| Фокусное расстояние (мм) | Диагональ (°) | Вертикальный (°) | По горизонтали (°) |
|---|---|---|---|
| 2 | 162.9 | 149.8 | 159.6 |
| 4 | 146.6 | 123.2 | 140.4 |
| 7 | 124.6 | 93.2 | 115.5 |
| 9 | 112.0 | 78.9 | 101.9 |
| 12 | 96.1 | 63.3 | 85.5 |
| 14 | 87.2 | 55.7 | 76.8 |
| 16 | 79.6 | 49.6 | 69.5 |
| 17 | 76.2 | 47.0 | 66.3 |
| 18 | 73.1 | 44.7 | 63.3 |
| 20 | 67.4 | 40.6 | 58.1 |
| 24 | 58.1 | 34.3 | 49.6 |
| 35 | 41.7 | 23.9 | 35.2 |
| 50 | 29.9 | 16.8 | 25.0 |
| 70 | 21.6 | 12.1 | 18.0 |
| 85 | 17.8 | 10.0 | 14.9 |
| 105 | 14.5 | 8.1 | 12.1 |
| 200 | 7.6 | 4.2 | 6.4 |
| 210 | 7.3 | 4.0 | 6.1 |
| 300 | 5.1 | 2.8 | 4.2 |
| 400 | 3.8 | 2.1 | 3.2 |
| 500 | 3.1 | 1.7 | 2.5 |
| 600 | 2.5 | 1.4 | 2.1 |
| 700 | 2.2 | 1.2 | 1.8 |
| 800 | 1.9 | 1.1 | 1.6 |
Кинематография и видеоигры
| Соотношение | Разрешение 1080p | Распространенное имя | Формат видео / объектив |
|---|---|---|---|
| 32:27 | 1280x1080p | DVCPRO HD | |
| 4:3 | 1440x1080p | ||
| 16:9 | 1920x1080p | Широкоэкранный | |
| 2:1 | 2160×1080 | 18:9 | Univisium |
| 64:27 | 2560x1080p | Ультра-широкоформатный | Синемаскоп / Анаморфный |
| 32:9 | 3840x1080p | Супер сверхширокий экран | Сверхширокий экран 3.6 / Анаморфный 3.6 |
Изменение угла обзора с течением времени (известное как масштабирование ), часто используется кинематографическая техника, часто в сочетании с движением камеры для создания “Долли зум “эффект, прославленный фильмом Головокружение. Использование широкого угла обзора может преувеличить воспринимаемую скорость камеры и является распространенной техникой в отслеживание выстрелов, фантомные аттракционы, и гоночные видеоигры. Смотрите также Поле зрения в видеоиграх.
Смотрите также
- Эквивалентное фокусное расстояние 35 мм
- Угол камеры
- Покрытие камеры
- Оператор
- Кинематографические приемы
- Поле зрения
- Кинопроизводство
- Установка нескольких камер
- Настройка одной камеры
- Видео производство
- Формат датчика изображения
- Фактор урожая
- Сверхширокие форматы
Примечания и ссылки
- ^ Тим Добберт (ноябрь 2012 г.). Matchmoving: The Invisible Art of Camera Tracking, 2nd Edition. Джон Вили и сыновья. п. 116. ISBN 9781118529669.
- ^ Нил Уэйн Норти (сентябрь 1916 г.). Фрэнк В. Чемберс (ред.). «Угол обзора линзы». Камера. Колумбийское фотографическое общество. 20 (9).
- ^ «Обзор объектива Canon EF 15mm f / 2.8 Fisheye». The-Digital-Picture.com. В архиве из оригинала 7 августа 2017 г.. Получено 1 мая 2018.
- ^ Эрнест МакКоллоу (1893). «Фотографическая топография». Промышленность: ежемесячный журнал, посвященный науке, технике и механике. Промышленная издательская компания, Сан-Франциско: 399–406.
- ^ Расчет поля зрения объектива камеры видеонаблюдения В архиве 2008-08-22 на Wayback Machine от JVSG, декабрь 2007 г.
- ^ Керр, Дуглас А. (2008). «Правильная точка поворота для панорамной фотографии» (PDF). Тыква. Получено 2014-03-20.
- ^ Пол ван Валри (2009). «Центр перспективы». Архивировано из оригинал 30 апреля 2009 г.. Получено 24 января 2010.
- ^ Холст, Г. (1998). Тестирование и оценка систем инфракрасного изображения (2-е изд.). Флорида: JCD Publishing, Вашингтон: SPIE.
- ^ Mazzetta, J.A .; Скопац, С. (2007). Автоматизированное тестирование датчиков ультрафиолетового, видимого и инфракрасного излучения с использованием общей оптики. Инфракрасные системы формирования изображений: анализ конструкции, моделирование и тестирование XVIII, Vol. 6543, стр. 654313-1 654313-14
- ^ Electro Optical Industries, Inc. (2005). EO TestLab Methadology. В Образование / Ссылка. «Архивная копия». Архивировано из оригинал на 2008-08-28. Получено 2008-05-22.CS1 maint: заархивированная копия как заголовок (ссылка на сайт).
- ^ Рэй, Сидней Ф. (1 мая 2018 г.). Прикладная фотографическая оптика: линзы и оптические системы для фотографии, кино, видео, электронных и цифровых изображений. Focal. ISBN 9780240515403. Получено 1 мая 2018 – через Google Книги.
- ^ Линн Уоррен, Энциклопедия фотографии ХХ века, стр. 211
- ^ Лэнгфорд, Майкл (1 мая 2018 г.). Базовая фотография. Focal Press. ISBN 9780240515922. Получено 1 мая 2018 – через Google Книги.
- ^ а б “Твой сайт”. www.photographywebsite.co.uk. Получено 1 мая 2018.
- ^ Райхманн, Майкл. «Действительно ли у широкоугольных объективов большая глубина резкости, чем у телеобъективов?». Архивировано из оригинал на 2011-06-10. Получено 2011-07-08.
- ^ Однако в большинстве цифровых фотоаппаратов со сменными объективами не используется размер 24 × 36 мм. датчики изображения и, следовательно, обеспечивают более узкие углы обзора, чем указано в таблице. Увидеть фактор урожая и подтема проблемы с цифровой камерой в статье о широкоугольные объективы для дальнейшего обсуждения.
- ^ Коллин, Джоэл С. (1993). Дисплей Retinal для приложений виртуальной среды. Труды общества отображения информации. XXIV. п. 827. Архивировано с оригинал на 2013-07-04. Получено 2014-04-27.
- ^ В примерах изображений используется объектив 5,1–15,3 мм, который производитель назвал 3-кратным зумом 24 мм (Ricoh Caplio GX100 В архиве 2009-06-01 на Wayback Machine )
внешняя ссылка
- Простое объяснение угла обзора и фокусного расстояния
- Угол обзора цифровых зеркальных фотоаппаратов с уменьшенным размером сенсора
- Фокусное расстояние и угол обзора
 Угол обзора камеры может быть измерен по горизонтали, вертикали или диагонали.
Угол обзора камеры может быть измерен по горизонтали, вертикали или диагонали.
В фотография, угол обзора (AOV ) описывает угловой протяженность данной сцены, которая отображается камерой . Он используется взаимозаменяемо с более общим термином поле зрения.
. Важно отличать угол обзора от угла охвата, который описывает диапазон углов, который может отображать объектив. Обычно круг изображения, создаваемый линзой, достаточно велик, чтобы полностью покрыть пленку или датчик, возможно, включая некоторое виньетирование к краю. Если угол обзора объектива не заполняет датчик, круг изображения будет виден, как правило, с сильным виньетированием по направлению к краю, а эффективный угол обзора будет ограничен углом обзора.
 В 1916 году Норти показал, как рассчитать угол обзора с помощью обычных плотницких инструментов. Угол, который он называет углом зрения, – это половинный угол или «угол, который прямая линия будет принимать от крайнего края поля зрения к центру линзы»; он отмечает, что производители линз используют вдвое больше этого угла.
В 1916 году Норти показал, как рассчитать угол обзора с помощью обычных плотницких инструментов. Угол, который он называет углом зрения, – это половинный угол или «угол, который прямая линия будет принимать от крайнего края поля зрения к центру линзы»; он отмечает, что производители линз используют вдвое больше этого угла.  В этом моделировании регулировка угла обзора и расстояния до камеры при сохранении объекта в кадре приводит к сильно различающимся изображениям. На расстояниях, приближающихся к бесконечности, световые лучи почти параллельны друг другу, что приводит к «сглаженному» изображению. На малых расстояниях и больших углах обзора объекты кажутся «укороченными».
В этом моделировании регулировка угла обзора и расстояния до камеры при сохранении объекта в кадре приводит к сильно различающимся изображениям. На расстояниях, приближающихся к бесконечности, световые лучи почти параллельны друг другу, что приводит к «сглаженному» изображению. На малых расстояниях и больших углах обзора объекты кажутся «укороченными».
Угол обзора камеры зависит не только от объектива, но и от сенсора. Цифровые датчики обычно меньше 35-миллиметровой пленки, и это приводит к тому, что объектив имеет более узкий угол обзора, чем у 35-миллиметровой пленки, с постоянным коэффициентом для каждого датчика (так называемый кроп-фактор ). В обычных цифровых камерах кроп-фактор может варьироваться от 1 (профессиональные цифровые SLR ) до 1,6 (потребительские SLR), от 2 (Micro Four Thirds ILC) до 6 (большинство компактные камеры ). Таким образом, стандартный 50-миллиметровый объектив для 35-миллиметровой фотографии действует как стандартный 50-миллиметровый «пленочный» объектив на профессиональных цифровых SLR, но будет действовать ближе к 80-миллиметровому объективу (1,6 x 50 мм) на многих цифровых зеркальных фотокамерах среднего размера, а 40 градусный угол зрения стандартного объектива 50 мм на пленочной камере эквивалентен объективу 80 мм на многих цифровых SLR.
Содержание
- 1 Расчет угла обзора камеры
- 1.1 Пример
- 1.2 Вывод формулы угла зрения
- 1.2.1 Макросъемка
- 2 Измерение поля зрения камеры
- 3 Типы линз и эффекты
- 3.1 Фокусное расстояние
- 3.2 Характеристики
- 3.3 Примеры
- 4 Общие углы обзора линз
- 5 Влияние размера сенсора («кроп-фактор»)
- 6 Кинематография и видеоигры
- 7 См. Также
- 8 Примечания и ссылки
- 9 Внешние ссылки
Расчет угла обзора камеры
Для объективов, проецирующих прямолинейных (не -пространственно-искаженные) изображения удаленных объектов, эффективное фокусное расстояние и размеры формата изображения полностью определяют угол обзора. Расчеты для линз, создающих непрямолинейные изображения, намного сложнее и, в конце концов, не очень полезны в большинстве практических приложений. (В случае объектива с искажением, например, объектива «рыбий глаз», более длинный объектив с искажением может иметь более широкий угол обзора, чем более короткий объектив с низким искажением). Угол обзора может измеряться по горизонтали ( от левого до правого края рамки), вертикально (сверху вниз) или по диагонали (от одного угла рамки к ее противоположному углу).
Для объектива, проецирующего прямолинейное изображение (сфокусированное на бесконечность, см. вывод), угол обзора (α) может быть рассчитан на основе выбранного размера (d) и эффективного фокусного расстояния (f) следующим образом:
-
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
d { displaystyle d}


Поскольку это тригонометрическая функция, угол обзора не изменяется совершенно линейно с обратной величиной фокусного расстояния. Однако, за исключением широкоугольных объективов, разумно приблизить α ≈ df { displaystyle alpha приблизительно { frac {d} {f}}}

Эффективное фокусное расстояние почти равно заявленному фокусному расстоянию объектива (F), за исключением макросъемки, где расстояние от объектива до объекта сравнимо с фокусным расстоянием. В этом случае необходимо учитывать коэффициент увеличения (м):
-
- f = F ⋅ (1 + m) { displaystyle f = F cdot (1 + m)}
- f = F ⋅ (1 + m) { displaystyle f = F cdot (1 + m)}
(В фотографии m { displaystyle m}

Угол обзора также можно определить с помощью таблиц FOV, бумажных или программных калькуляторов линз.
 Логарифмические графики фокусного расстояния и кроп-фактора в зависимости от диагонального, горизонтального и вертикального углов обзора для пленки или датчиков Соотношение сторон 3: 2 и 4: 3. Желтая линия показывает пример, где 18 мм на 3: 2 APS-C эквивалентно 27 мм и дает вертикальный угол 48 градусов.
Логарифмические графики фокусного расстояния и кроп-фактора в зависимости от диагонального, горизонтального и вертикального углов обзора для пленки или датчиков Соотношение сторон 3: 2 и 4: 3. Желтая линия показывает пример, где 18 мм на 3: 2 APS-C эквивалентно 27 мм и дает вертикальный угол 48 градусов.
Пример
Рассмотрим камеру 50 мм с объективом, имеющим фокусное расстояние F = 50 мм. Размеры изображения формата 35 мм составляют 24 мм (по вертикали) × 36 мм (по горизонтали), что дает диагональ около 43,3 мм.
В фокусе на бесконечность, f = F, углы обзора следующие:
- по горизонтали, α h = 2 arctan h 2 f = 2 arctan 36 2 × 50 ≈ 39,6 ∘ { displaystyle alpha _ {h} = 2 arctan { frac {h} {2f}} = 2 arctan { frac {36} {2 times 50}} приблизительно 39,6 ^ { circ}}
- по вертикали α v = 2 arctan v 2 f = 2 arctan 24 2 × 50 ≈ 27,0 ∘ { displaystyle alpha _ {v} = 2 arctan { frac {v} {2f}} = 2 arctan { frac {24} {2 times 50}} приблизительно 27,0 ^ { circ}}
- по диагонали, α d = 2 арктангенса d 2 f = 2 арктангенса 43,3 2 × 50 ≈ 46,8 ∘ { displaystyle alpha _ {d} = 2 arctan { frac {d} {2f}} = 2 arctan { frac {43,3} {2 times 50}} приблизительно 46,8 ^ { circ} }
Вывод формулы угла зрения
Рассмотрим прямолинейный объектив в камере, используемый для фотографирования объекта на расстоянии S 1 { displaystyle S_ {1}}



Теперь α / 2 { displaystyle alpha / 2}

-
- углом α { displaystyle alpha}
- «противоположной» стороной прямоугольный треугольник, d / 2 { displaystyle d / 2}
(половина размера формата фильма)
- “смежная” сторона, S 2 { displaystyle S_ {2}}
(расстояние от линзы до плоскости изображения)
- углом α { displaystyle alpha}
Используя базовую тригонометрию, находим:
-
- tan (α / 2) = d / 2 S 2. { displaystyle tan ( alpha / 2) = { frac {d / 2} {S_ {2}}}.}
- tan (α / 2) = d / 2 S 2. { displaystyle tan ( alpha / 2) = { frac {d / 2} {S_ {2}}}.}
который мы можем решить относительно α, давая:
-
- α = 2 arctan d 2 S 2 { displaystyle alpha = 2 arctan { frac {d} {2S_ {2}}}}
- α = 2 arctan d 2 S 2 { displaystyle alpha = 2 arctan { frac {d} {2S_ {2}}}}
Чтобы проецировать четкое изображение удаленных объектов, S 2 { displaystyle S_ {2}}

-
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
где f = F { displaystyle f = F}
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
Обратите внимание, что угол обзора незначительно меняется, когда фокус не находится на бесконечности (см. дыхание (линза) ), определяемый как S 2 = S 1 f S 1 – f { displaystyle S_ {2} = { frac {S_ {1} f} {S_ {1} -f}}}
Макросъемка
Что касается макросъемки, мы не можем игнорировать разницу между S 2 { displaystyle S_ {2}}

-
- 1 F = 1 S 1 + 1 S 2 { displaystyle { frac {1} {F}} = { frac {1} {S_ {1}}} + { frac {1} {S_ {2}}}}
.
- 1 F = 1 S 1 + 1 S 2 { displaystyle { frac {1} {F}} = { frac {1} {S_ {1}}} + { frac {1} {S_ {2}}}}
Из определения увеличения, m = S 2 / S 1 { displaystyle m = S_ {2} / S_ { 1}}

-
- S 2 = F ⋅ (1 + m) { displaystyle S_ {2} = F cdot (1 + m)}
- S 2 = F ⋅ (1 + m) { displaystyle S_ {2} = F cdot (1 + m)}
Определение f = S 2 { displaystyle f = S_ {2}}
-
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
где f = F ⋅ (1 + m) { displaystyle f = F cdot (1 + m)}
.
- α = 2 arctan d 2 f { displaystyle alpha = 2 arctan { frac {d} {2f}}}
Второй эффект, который играет роль в макросъемке, – это асимметрия объектива (асимметричный объектив – это объектив, у которого диафрагма кажется, что имеет разные размеры, если смотреть спереди и сзади). Асимметрия линзы вызывает смещение между узловой плоскостью и положением зрачка. Эффект можно количественно оценить с помощью отношения (P) между кажущимся диаметром выходного зрачка и диаметром входного зрачка. Полная формула для угла обзора теперь выглядит следующим образом:
-
- α = 2 arctan d 2 F ⋅ (1 + m / P) { displaystyle alpha = 2 arctan { frac {d} {2F cdot (1 + m / P)}}}
- α = 2 arctan d 2 F ⋅ (1 + m / P) { displaystyle alpha = 2 arctan { frac {d} {2F cdot (1 + m / P)}}}
Измерение поля зрения камеры
 Схема оптического устройства на основе коллиматора, используемого для измерения поля зрения камеры.
Схема оптического устройства на основе коллиматора, используемого для измерения поля зрения камеры.
В индустрии оптических приборов Чаще всего используется термин поле зрения (FOV), хотя измерения по-прежнему выражаются в углах. Оптические тесты обычно используются для измерения поля зрения UV, видимого и инфракрасного (длины волн около 0,1–20 мкм в электромагнитном спектре ) датчиков и камер.
Целью этого теста является измерение горизонтального и вертикального поля зрения объектива и датчика, используемых в системе формирования изображения, когда фокусное расстояние объектива или размер датчика неизвестны (то есть, когда вычисление выше не применимо сразу). Хотя это один из типичных методов, которые промышленность оптики использует для измерения поля обзора, существует множество других возможных методов.
УФ / видимый свет от интегрирующей сферы (и / или другого источника, такого как черное тело ) фокусируется на квадратной тестовой мишени в фокальная плоскость коллиматора (зеркала на схеме), так что виртуальное изображение тестовой цели будет бесконечно удалено тестируемой камерой. Тестируемая камера воспринимает реальное изображение виртуального изображения цели, и полученное изображение отображается на мониторе.
 Отображение на мониторе считанного изображения с тестируемой камеры
Отображение на мониторе считанного изображения с тестируемой камеры
Воспринимаемое изображение, которое включает цель, отображается на мониторе, где его можно измерить. Размеры отображения полного изображения и части изображения, которая является целью, определяются путем осмотра (измерения обычно производятся в пикселях, но также могут быть дюймы или сантиметры).
-
- D { displaystyle D}
= размер полного изображения
- d { displaystyle d}
= размер изображения цели
- D { displaystyle D}
удаленное виртуальное изображение коллиматора цель имеет определенный угол, называемый угловой протяженностью цели, который зависит от фокусного расстояния коллиматора и размера цели. Предполагая, что воспринимаемое изображение включает в себя всю цель, угол обзора камеры, ее FOV, равен этой угловой протяженности цели, умноженной на отношение полного размера изображения к размеру целевого изображения.
Угловой размер цели равен:
-
- α = 2 arctan L 2 fc { displaystyle alpha = 2 arctan { frac {L} {2f_ {c}}}}
- α = 2 arctan L 2 fc { displaystyle alpha = 2 arctan { frac {L} {2f_ {c}}}}
-
- где L { displaystyle L}
– это размер цели, а fc { displaystyle f_ {c}}
– фокусное расстояние коллиматора.
- где L { displaystyle L}
В этом случае общее поле зрения составляет приблизительно:
-
- FOV = α D d { displaystyle mathrm {FOV} = alpha { frac {D} {d}}}
- FOV = α D d { displaystyle mathrm {FOV} = alpha { frac {D} {d}}}
или, более точно, если система формирования изображения прямолинейна :
-
- FOV = 2 arctan LD 2 fcd { displaystyle mathrm {FOV} = 2 arctan { frac {LD} {2f_ {c} d}}}
- FOV = 2 arctan LD 2 fcd { displaystyle mathrm {FOV} = 2 arctan { frac {LD} {2f_ {c} d}}}
Этот расчет может быть горизонтальным или вертикальным полем обзора, в зависимости от того, как цель и изображение измеряются.
Типы линз и эффекты
Фокусное расстояние
 Как фокусное расстояние влияет на перспективу: различные фокусные расстояния при одинаковом размере поля, достигаемом разными камерами -субъектные расстояния. Обратите внимание, что чем короче фокусное расстояние и больше угол обзора, искажение перспективы и различия в размерах увеличиваются.
Как фокусное расстояние влияет на перспективу: различные фокусные расстояния при одинаковом размере поля, достигаемом разными камерами -субъектные расстояния. Обратите внимание, что чем короче фокусное расстояние и больше угол обзора, искажение перспективы и различия в размерах увеличиваются.
Объективы часто называют терминами, выражающими их угол зрения:
- линзы Fisheye, типичные фокусные расстояния составляют от 8 мм до 10 мм для круглых изображений и 15–16 мм для полнокадровых изображений. До 180 ° и выше.
- A круглая линза «рыбий глаз» (в отличие от полнокадровой линзы «рыбий глаз») является примером линзы, у которой угол покрытия меньше угла обзора. Изображение, проецируемое на пленку, является круглым, потому что диаметр проецируемого изображения уже, чем диаметр, необходимый для покрытия самой широкой части пленки.
- Сверхширокоугольный объектив – это прямолинейный, который является менее 24 мм с фокусным расстоянием в формате пленки 35 мм, здесь 14 мм дает 114 °, а 24 мм дает 84 °.
- Широкоугольные объективы (24–35 мм на 35 мм формат пленки) охватывает от 84 ° до 64 °
- Обычные или стандартные линзы (36–60 мм в формате пленки 35 мм) охватывают от 62 ° до 40 °
- Длиннофокусные линзы (любые объектив с фокусным расстоянием больше, чем диагональ используемой пленки или датчика) обычно имеют угол обзора 35 ° или меньше. Поскольку фотографы обычно сталкиваются только с подтипом телеобъективов и, на обычном фотографическом языке их называют:
- «средний телеобъектив», фокусное расстояние от 85 мм до 250 мм в 35 формат пленки с диапазоном от 30 ° до 10 °
- «Супертелеобъектив» (более 300 мм в формате пленки 35 мм) обычно охватывает угол от 8 ° до менее 1 °
Зум-объективы являются особый случай, когда фокусное расстояние и, следовательно, угол обзора объектива можно изменять механически, не снимая объектив с камеры.
Характеристики
При заданном расстоянии от камеры до объекта более длинные линзы увеличивают объект в большей степени. Для данного увеличения объекта (и, следовательно, различного расстояния между камерой и объектом) кажется, что более длинные линзы сжимают расстояние; кажется, что более широкие линзы увеличивают расстояние между объектами.
Еще одним результатом использования широкоугольного объектива является более заметное перспективное искажение, когда камера не выровнена перпендикулярно объекту: параллельные линии сходятся с той же скоростью, что и в нормальный объектив, но больше сходится из-за более широкого общего поля. Например, кажется, что здания падают назад намного сильнее, когда камера направлена вверх от уровня земли, чем при съемке с обычным объективом на том же расстоянии от объекта, поскольку большая часть здания объекта видна в широком диапазоне. угол выстрела.
Поскольку для разных объективов обычно требуется разное расстояние между камерой и объектом для сохранения размера объекта, изменение угла обзора может косвенно исказить перспективу, изменяя видимый относительный размер объекта и передний план.
Если размер изображения объекта остается прежним, то при любой заданной диафрагме все объективы, широкоугольные и длинные линзы, будут давать одинаковую глубину резкости.
Примеры
пример того, как выбор объектива влияет на угол обзора.
 объектив 28 мм, 65,5 ° × 46,4 ° объектив 28 мм, 65,5 ° × 46,4 ° |
 объектив 50 мм, 39,6 ° × 27,0 ° объектив 50 мм, 39,6 ° × 27,0 ° |
 объектив 70 мм, 28,9 ° × 19,5 ° объектив 70 мм, 28,9 ° × 19,5 ° |
 объектив 210 мм, 9,8 ° × 6,5 ° объектив 210 мм, 9,8 ° × 6,5 ° |
Общие углы обзора линз
В этой таблице показаны диагональный, горизонтальный и вертикальный углы обзора в градусах для линз, создающих прямолинейные изображения, при использовании формата 36 мм × 24 мм (то есть 135 пленка или полнокадровый 35 мм цифровой с шириной 36 мм, высотой 24 мм и диагональю 43,3 мм для d в формуле выше). Цифровые компактные камеры иногда указывают фокусные расстояния своих объективов в эквиваленте 35 мм, которые можно использовать в этой таблице.
Для сравнения: зрительная система человека воспринимает угол зрения примерно 140 ° на 80 °.
| Фокусное расстояние (мм) | Диагональ (°) | По вертикали (°) | По горизонтали (°) |
|---|---|---|---|
| 0 | 180,0 | 180,0 | 180,0 |
| 2 | 169,4 | 161,1 | 166,9 |
| 12 | 122,0 | 90,0 | 111,1 |
| 14 | 114,2 | 81,2 | 102,7 |
| 16 | 107,1 | 73,9 | 95,1 |
| 20 | 94,5 | 61,9 | 82,4 |
| 24 | 84,1 | 53,1 | 73,7 |
| 35 | 63,4 | 37,8 | 54,4 |
| 50 | 46,8 | 27,0 | 39,6 |
| 70 | 34,4 | 19,5 | 28,8 |
| 85 | 28,6 | 16,1 | 23,9 |
| 105 | 23,3 | 13,0 | 19,5 |
| 200 | 12,3 | 6,87 | 10,3 |
| 300 | 8,25 | 4,58 | 6,87 |
| 400 | 6,19 | 3,44 | 5,15 |
| 500 | 4,96 | 2,75 | 4,12 |
| 600 | 4,13 | 2,29 | 3,44 |
| 700 | 3,54 | 1,96 | 2,95 |
| 800 | 3,10 | 1,72 | 2,58 |
| 1200 | 2,07 | 1,15 | 1,72 |
 Пять изображений с использованием 24, 28, 35, 50 и 72 эквивалентная длина увеличения в мм, портретный формат, для иллюстрации углов обзора
Пять изображений с использованием 24, 28, 35, 50 и 72 эквивалентная длина увеличения в мм, портретный формат, для иллюстрации углов обзора  Пять изображений с использованием функции эквивалентного шага масштабирования 24, 28, 35, 50 и 72 мм для иллюстрации углов обзора
Пять изображений с использованием функции эквивалентного шага масштабирования 24, 28, 35, 50 и 72 мм для иллюстрации углов обзора
Эффекты размера сенсора («кроп-фактор»)
Как отмечалось выше, угол обзора камеры зависит не только от объектива, но и от используемого датчика. Цифровые датчики обычно меньше 35-миллиметровой пленки, из-за чего объектив обычно ведет себя так же, как и объектив с большим фокусным расстоянием, и имеет более узкий угол обзора, чем у 35-мм пленки, с постоянным коэффициентом для каждого датчика (так называемый кроп-фактор ). В повседневных цифровых камерах кроп-фактор может варьироваться от 1 (профессиональные цифровые SLR ) до 1,6 (SLR среднего класса) и от 3 до 6 для компактных камер. Таким образом, стандартный 50-миллиметровый объектив действует как 50-миллиметровый стандартный «пленочный» объектив даже на профессиональных цифровых SLR, но на многих он будет действовать ближе к 75-мм (1,5 × 50 мм Nikon) или 80 мм (1,6 x 50 мм Canon). зеркалки среднего размера, а угол обзора стандартного 50-мм объектива пленочной камеры в 40 градусов эквивалентен объективу 28–35 мм на многих цифровых зеркальных фотокамерах.
В таблице ниже показаны горизонтальный, вертикальный и диагональный углы обзора в градусах при использовании формата 22,2 мм × 14,8 мм (то есть Canon DSLR с размером кадра APS-C ) и диагональ 26,7 мм.
| Фокусное расстояние (мм) | Диагональ (°) | По вертикали (°) | По горизонтали (°) |
|---|---|---|---|
| 2 | 162,9 | 149,8 | 159,6 |
| 4 | 146,6 | 123,2 | 140,4 |
| 7 | 124,6 | 93,2 | 115,5 |
| 9 | 112,0 | 78,9 | 101,9 |
| 12 | 96,1 | 63,3 | 85,5 |
| 14 | 87,2 | 55,7 | 76,8 |
| 16 | 79,6 | 49,6 | 69,5 |
| 17 | 76,2 | 47,0 | 66,3 |
| 18 | 73,1 | 44,7 | 63,3 |
| 20 | 67,4 | 40,6 | 58,1 |
| 24 | 58,1 | 34,3 | 49,6 |
| 35 | 41,7 | 23,9 | 35,2 |
| 50 | 29,9 | 16,8 | 25,0 |
| 70 | 21,6 | 12,1 | 18,0 |
| 85 | 17,8 | 10,0 | 14,9 |
| 105 | 14,5 | 8,1 | 12,1 |
| 200 | 7,6 | 4.2 | 6.4 |
| 210 | 7.3 | 4.0 | 6.1 |
| 300 | 5.1 | 2,8 | 4,2 |
| 400 | 3,8 | 2,1 | 3,2 |
| 500 | 3,1 | 1,7 | 2,5 |
| 600 | 2,5 | 1,4 | 2,1 |
| 700 | 2.2 | 1,2 | 1,8 |
| 800 | 1,9 | 1,1 | 1,6 |
Кинематография и видеоигры
| Соотношение | Разрешение 1080p | Общее название | Формат видео / объектив |
|---|---|---|---|
| 32:27 | 1280x1080p | DVCPRO HD | |
| 4: 3 | 1440x1080p | ||
| 16: 9 | 1920x1080p | Широкоэкранный | |
| 2: 1 | 2160×1080 | 18: 9 | Univisium |
| 64:27 | 2560x1080p | Ультра-широкоэкранный | Cinemascope / Анаморфотный |
| 32: 9 | 3840x1080p | Сверхширокоформатный | Сверхширокий экран 3,6 / Анаморфный 3,6 |
Изменение угла просмотр во времени (известный как масштабирование ) – часто используемый кинематографический прием, часто сочетающийся с движением камеры для создания знаменитого эффекта «масштабирование тележки » по фильму Vertigo. Использование широкого угла обзора может преувеличить воспринимаемую скоростью камеры и является распространенной техникой в отслеживающих снимках, фантомных поездках и гоночных видеоиграх. См. Также Поле зрения в видеоиграх.
См. Также
Примечания и ссылки
- ^Тим Добберт (Ноябрь 2012 г.). Matchmoving: The Invisible Art of Camera Tracking, 2nd Edition. Джон Вили и сыновья. п. 116. ISBN 9781118529669.
- ^Нил Уэйн Норти (сентябрь 1916 г.). Фрэнк В. Чемберс (ред.). «Угол обзора линзы». Камера. Колумбийское фотографическое общество. 20 (9).
- ^”Обзор объектива Canon EF 15mm f / 2.8 Fisheye”. The-Digital-Picture.com. Архивировано 7 августа 2017 г. из оригинала. Архивировано 1 мая 2018 г.
- ^Эрнест МакКоллоу (1893). “Фотографическая топография”. Промышленность: ежемесячный журнал, посвященный науке, технике и механике. Industrial Publishing Company, Сан-Франциско: 399–406.
- ^Расчеты объектива камеры видеонаблюдения Архивировано 22 августа 2008 г. на Wayback Machine компанией JVSG, декабрь, 2007
- ^Керр, Дуглас А. (2008). «Правильная точка поворота для панорамной фотографии» (PDF). Тыква. Проверено 20 марта 2014 г.
- ^Пол ван Валри (2009). «Центр перспективы». Архивировано с оригинала 30 апреля 2009 г. Получено 24 января 2010 г.
- ^Holst, G.C. (1998). Тестирование и оценка систем инфракрасного изображения (2-е изд.). Флорида: JCD Publishing, Вашингтон: SPIE.
- ^Mazzetta, J.A.; Скопац, С. (2007). Автоматизированное тестирование ультрафиолетовых, видимых и инфракрасных датчиков с использованием общей оптики. Инфракрасные системы формирования изображений: анализ конструкции, моделирование и тестирование XVIII, Vol. 6543, стр. 654313-1 654313-14
- ^Electro Optical Industries, Inc. (2005). EO TestLab Methadology. В образовании / Ref. «Архивная копия». Архивировано с оригинального 28.08.2008. Проверено 22 мая 2008 г. CS1 maint: заархивированная копия как заголовок (ссылка ).
- ^Рэй, Сидни Ф. (1 мая 2018 г.). Прикладная фотографическая оптика: линзы и оптические системы для фотографии, Пленка, видео, электронные и цифровые изображения. Focal. ISBN 9780240515403. Получено 1 мая 2018 г. – через Google Книги.
- ^Линн Уоррен, Энциклопедия фотографии 20-го века, страница 211
- ^Лэнгфорд, Майкл (1 мая 2018 г.). Basic Photography. Focal Press. ISBN 9780240515922. Получено 1 мая 2018 г. – через Google Книги.
- ^ «Ваш сайт». Www.photographywebsite.co.uk. Проверено 1 мая 2018 г.
- ^Райхманн, Майкл. «Действительно ли широкоугольные объективы имеют большую глубину резкости, чем телеобъективы?». Архивировано из оригинала 10.06.2011. Проверено 08.07.2011.
- ^Однако в большинстве цифровых фотоаппаратов со сменными объективами не используются датчики изображения 24 × 36 мм и, следовательно, обеспечивают более узкие углы обзора, чем указано в таблице. См. кроп-фактор и подтема цифровые камеры вопросы в статье о широкоугольных объективах для дальнейшего обсуждения.
- ^Коллин, Джоэл С. (1993). Сетчатый дисплей для приложений виртуальной среды. Труды общества отображения информации. XXIV . п. 827. Архивировано из оригинала 04.07.2013. Проверено 27 апреля 2014 г.
- ^В примерах изображений используется объектив 5,1–15,3 мм, который производитель назвал 3-кратным зумом 24 мм (Ricoh Caplio GX100 Архивировано 2009 г. -06-01 на Wayback Machine )
Внешние ссылки
Угол изображения
© 2015 Vasili-photo.com
Угол изображения или угловое поле объектива – это угол, образованный лучами, соединяющими крайние противоположные точки кадра с оптическим центром объектива. Иными словами, это максимальный угловой размер объекта, который может быть снят с помощью данного объектива.
Широкий угол изображения позволяет объективу охватить больше пространства за счёт малого масштаба изображения. Узкий угол изображения показывает меньше пространства, но в большем масштабе.
Поскольку кадр имеет прямоугольную форму, следует различать угловое поле, измеряемое по горизонтали, по вертикали и по диагонали кадра. В технических характеристиках фотографических объективов чаще всего указывается наибольший, т.е. диагональный угол изображения.
Величина углового поля обратно пропорциональна фокусному расстоянию объектива и прямо пропорциональна размеру светочувствительного материала (плёнки или матрицы), т.е. чем длиннее объектив и чем меньше матрица, тем меньше угол изображения, и наоборот, чем короче объектив и чем больше матрица, тем угол изображения больше.
Объективы, угол изображения которых составляет 40-60°, считаются нормальными или стандартными. Если угол изображения больше 60°, объектив является короткофокусным или широкоугольным, а если угол меньше 40° – длиннофокусным или телеобъективом.
Как узнать угол изображения для конкретного объектива? Это не сложно. Ниже вы сможете ознакомиться с формулами для расчёта углового поля объектива, а в случае если математические подробности вам не слишком интересны, у вас есть возможность сразу перейти к интерактивному калькулятору, который способен выполнить все вычисления за вас.
Расчёт угла изображения
Чтобы найти угол изображения, достаточно знать фокусное расстояние объектива и линейные размеры матрицы. Угол изображения рассчитывается по формуле:
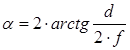 , где
, где
α – угол изображения (угловое поле) в радианах;
d – расстояние между крайними точками кадра (ширина, высота или диагональ) в миллиметрах;
f – фокусное расстояние объектива в миллиметрах.
Как видите, школьная тригонометрия действительно может пригодиться в жизни.
Для примера найдём диагональный угол изображения для стандартного объектива с фокусным расстоянием 50 мм, установленного на полнокадровую камеру. Размеры полного кадра 36 × 24 мм. Через теорему Пифагора находим диагональ кадра:
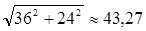 мм.
мм.
Подставляем длину диагонали и фокусное расстояние в формулу углового поля и получаем:
 рад.
рад.
Чтобы перевести ответ из радиан в градусы, достаточно умножить его на 180°/π (грубо говоря, в одном радиане содержится примерно 57,3 градуса). Таким образом, угол изображения будет равен 46,8°.
Зная угловое поле объектива, можно рассчитать максимальный линейный размер объекта, вписывающегося в кадр. Очевидно, что в отличие от углового поля, линейный охват пространства напрямую зависит от расстояния до объекта. Для расчёта линейного поля используется следующая формула:
D = 2 • R • tg (α / 2), где
D – охват пространства (линейное поле),
R – расстояние до объекта.
Например, на расстоянии 10 м охват пространства для уже упоминавшегося 50-мм объектива на полнокадровой камере будет равен:
2 • 10 • tg (46,8 / 2) ≈ 8,7 м.
Дабы не тратить время на все эти тригонометрические расчёты можно воспользоваться специальным калькулятором, но прежде я должен сделать одну важную оговорку.
Фокусировка и фокусное расстояние
Приведённая выше формула углового поля предполагает, что объектив сфокусирован на бесконечность. Лишь в этом случае эффективное фокусное расстояние объектива соответствует номинальному. При фокусировке объектива на более близких объектах эффективное фокусное расстояние может изменяться в определённых пределах, что влечёт за собой пропорциональное изменение угла обзора. В большинстве случаев плавание фокусного расстояния весьма незначительно и им можно смело пренебречь, однако при макросъёмке, когда расстояние до объекта сопоставимо с фокусным расстоянием объектива, эффект изменения угла обзора может стать вполне очевидным.
В идеале нам следовало бы подставлять в формулу значение именно эффективного фокусного расстояния для каждой конкретной дистанции фокусировки, но, к сожалению, это не всегда возможно.
Расчёт эффективного фокусного расстояния объектива сравнительно прост и прямолинеен только для классических фиксов, фокусировка которых осуществляется посредством выдвижения вперёд всего оптического блока. Иными словами, их эффективное фокусное расстояние увеличивается по мере увеличения масштаба съёмки, а угол обзора соответственно уменьшается. Эффективное фокусное расстояние в данном случае можно найти по формуле:
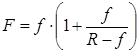 , где
, где
F – эффективное фокусное расстояние;
f – номинальное фокусное расстояние;
R – дистанция фокусировки.
Впрочем, для большинства современных объективов эта формула практически бесполезна, поскольку при внутренней фокусировке эффективное фокусное расстояние может меняться самым неожиданным образом. Обычно объектив стараются проектировать так, чтобы по возможности свести к минимуму эффект изменения угла обзора при наводке на резкость. Так, многие современные объективы сохраняют угол обзора практически неизменным вне зависимости от дистанции фокусировки. Некоторые зумы имеют парадоксальную тенденцию к незначительному увеличению угла обзора на малых фокусировочных дистанциях. То есть по сравнению с традиционными объективами они ведут себя достаточно противоестественно.
Впрочем, повторюсь: при съёмке с нормальных дистанций всем этим колебаниям не стоит придавать слишком большого значения.
Калькулятор угла изображения
Настоящий калькулятор позволяет определить угол обзора любого объектива, а также линейный охват пространства в зависимости от расстояния до объекта съёмки.
Для начала вам необходимо указать следующие параметры:
Фокусное расстояние
Истинное (не эквивалентное!) фокусное расстояние объектива в миллиметрах.
Формат
Формат матрицы фотоаппарата. Выберите нужный вариант из выпадающего списка. В скобках указан кроп-фактор.
Расстояние до объекта
Для вычисления линейного охвата пространства необходимо указать расстояние до объекта съёмки в метрах.
При желании вы можете также включить опцию «учитывать изменение фокусного расстояния при фокусировке». В этом случае калькулятор примет в расчёт увеличение эффективного фокусного расстояния по мере уменьшения дистанции фокусировки. Дистанцией фокусировки будет считаться расстояние до объекта, указанное ранее. Напомню, что это работает только при использовании традиционных объективов с фиксированным фокусным расстоянием. Если вы пользуетесь современным объективом с внутренней фокусировкой или плавающими элементами, вам стоит проигнорировать данный пункт.
Исходные данные
Угол изображения
| по горизонтали | 37,8° |
| по вертикали | 25,8° |
| по диагонали | 44,8° |
Охват пространства на расстоянии 5 м
| по горизонтали | 3,4 м |
| по вертикали | 2,3 м |
| по диагонали | 4,1 м |
Точность
Точность всех этих вычислений не слишком высока. Причин тому несколько: во-первых, истинное фокусное расстояние объектива может несколько отличаться от номинального (разница может доходить до 5%); во-вторых, как уже было сказано выше, эффективное фокусное расстояние может изменяться при фокусировке; в-третьих, размер сенсора также не вполне постоянен даже в пределах одного формата, и, наконец, в-четвёртых, определённое влияние на угол обзора оказывает дисторсия объектива, которую очень сложно учесть при расчётах.
Словом, несмотря на то, что в технических характеристиках объективов принято указывать углы обзора с точностью до десятой доли градуса, не стоит доверять этим цифрам безоговорочно.
Объективы типа «рыбий глаз»
Формула углового поля годится только для условно ортоскопических объективов, т.е. обладающих лишь незначительной дисторсией. К объективам типа «рыбий глаз» (fisheye) она неприменима.
В сущности, существуют две основные группы объективов, называемых fisheye: циркулярные и диагональные. Циркулярные объективы имеют угол обзора около 180° во всех направлениях. В этом случае круг изображения оказывается как бы вписанным в прямоугольник кадра. При использовании же диагональных объективов изображение заполняет кадр целиком, а угол обзора составляет 180° по диагонали кадра.
Спасибо за внимание!
Василий А.
Post scriptum
Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.
Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.
Желаю удачи!
|
Дата публикации: 30.11.2015 |
 |
Вернуться к разделу “Матчасть”
Перейти к полному списку статей
- Главная
- /
- Техподдержка
- /
- Справочные материалы
Справочные материалы
Углы обзора видеокамер, фокусные расстояния объективов
Одним из важнейших параметров при выборе камеры видеонаблюдения является угол обзора объектива. Этот параметр характеризует ширину той картины, будет охвачена камерой. Расчет угла обзора, при этом, вовсе не является сложным инженерным вычислением, и может быть выполнен даже начинающим специалистом.
От чего зависит угол обзора камеры?
– от двух основных параметров:
1. Фокусное расстояние. Оно является величиной, обратно пропорциональной углу обзора: чем больше фокусное расстояние объектива, тем меньше угол обзора. Таким образом, камеры длинным фокусным расстоянием применяются, как правило, для – охраны периметра или идентификации государственных номерных знаков. Существует ещё одна особенность – глубина резкости, чем больше величина f= фокусного расстояния тем выше требования к линзам объектива.
Фокусное расстояние, в свою очередь, зависит от размера матрицы, величины наблюдаемого объекта и расстояния, на которое объект удален объект от камеры (если объектов несколько, то берется расстояние до самого дальнего).

Для расчета оптимального фокусного расстояния применяется следующая формула: f= h*S/Н или F= v*S/V, где h – размер горизонтальной стороны матрицы; S – расстояние до объекта слежения; H – размер объекта наблюдения по горизонтали; v – размер вертикальной стороны матрицы; V – размер объекта наблюдения по вертикали.
Таким образом, для расчетов могут применяться или вертикальные размеры матрицы и наблюдаемого объекта, или горизонтальные параметры.
2. Размер матрицы. Как указано выше, данный параметр влияет и на угол обзора, и на оптимальное фокусное расстояние. Величина сенсора прямо пропорциональна углу обзора – чем больше матрица, тем больше угол обзора. Например, камеры с матрицей 1/2.7 будут иметь больший угол обзора, чем устройства с матрицей 1/3. Широкоугольные камеры применяются для наблюдения за вытянутыми вширь площадями, например, за территорией, прилегающей к предприятию.
Как рассчитать угол обзора?
Для расчета угла обзора используется формула α = 2arctg(d/2F), где α – угол обзора объектива; d – размер матрицы; f – фокусное расстояние.
Соответственно, исходя из того, какие параметры были использованы при расчете фокусного расстояния – вертикальные или горизонтальные – рассчитывается вертикальный или горизонтальный угол обзора. Специалисты по проектированию и монтажу систем видеонаблюдения, однако, не рассчитывают угол обзора вручную, а используют готовые калькуляторы и таблицы. Ниже приведены таблицы, в которых содержатся значения угла обзора для наиболее распространенных размеров матрицы в соотношении с зонами детализации:
1. Наблюдение: объект занимает от 25 до 30 % высоты экрана. В этом масштабе различаются характерные детали объекта, например, цвет волос, одежда.
2. Узнавание: объект занимает как минимум 50 % высоты экрана, что позволяет с высокой долей вероятности определить, находился ли этот объект в зоне наблюдения ранее.
3. Идентификация: объект занимает 100 % высоты экрана, качество изображения и уровень детализации достаточны для однозначного установления личности.















