Как найти угол онлайн бесплатно

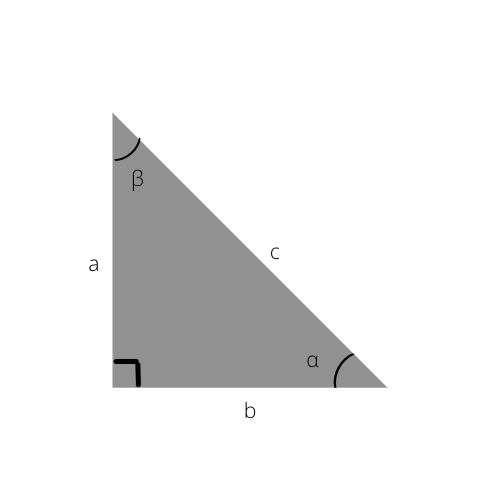
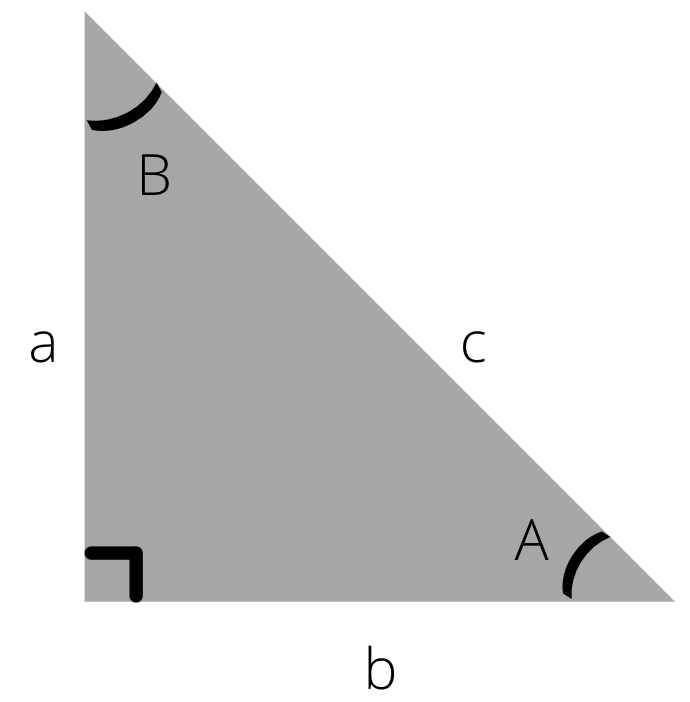
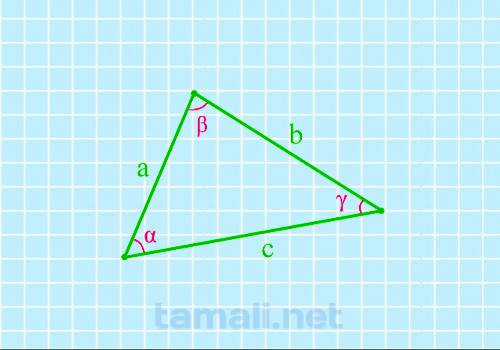
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

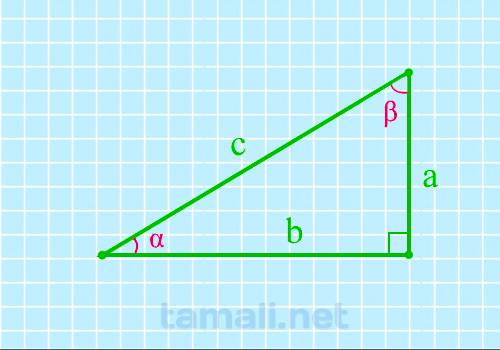
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

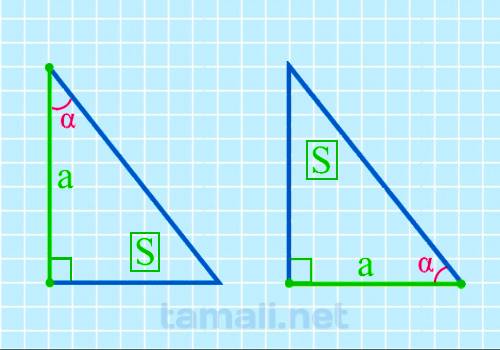
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

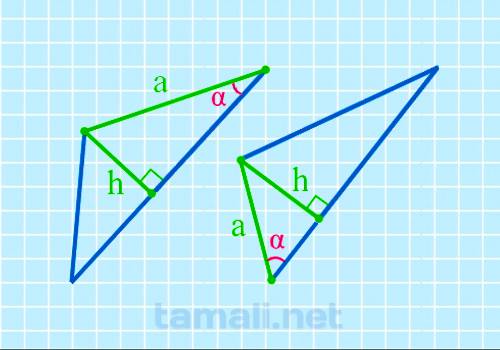
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

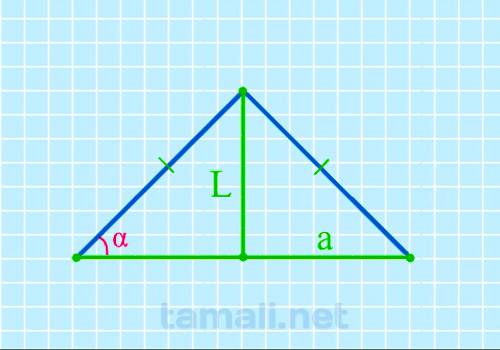
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

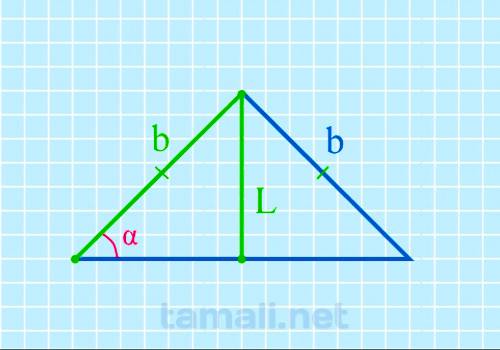
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

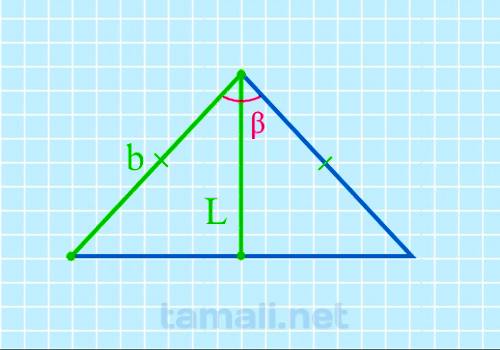
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

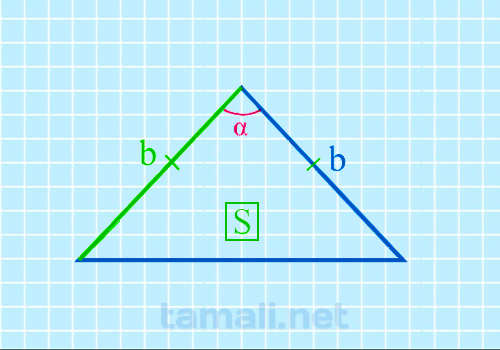
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

, откуда

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Углы – это измеряемые в градусах (радианах и пр.) геометрические фигуры, включающие в себя вершину и пару выходящих из нее лучей. Они могут быть составными элементами различных плоских и объемных фигур. Углы могут быть развернутыми (180 градусов), прямыми (90 градусов), острыми (меньше 90) и тупыми (больше 90).

Равными углами являются такие углы, которые при наложении показывают полное совпадение. Два угла могут называться смежными при наличии у них одной общей стороны.

Если два луча совпадают, можно говорить об угле равном 0 градусов. При вращении одного из лучей величина угла изменяется в сторону увеличения до тех пор, пока два луча вновь не совпадут. В этом случае угол равен 360 градусов.

Измеряют углы специальным изобретенным в древнем Вавилоне инструментом транспортиром, прибором с двумя шкалами, угломерной и прямолинейной. Кроме него для выяснения через замер углов положение корабля в море использовался гониометр и секстант. В строительном теодолите также задействуется метод замера углов. Библейский «посох Якова» служил для наблюдений астрономического характера.

Укажите размеры:

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

β
α

a
b
c

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

tg alpha = dfrac{a}{b}

• tg α – тангенс угла α
• a – противолежащий катет
• b – прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x. Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

angle alpha + angle beta + angle gamma = 180°

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

angle alpha = 90° – angle beta

angle beta = 90° – angle alpha

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла – острые.

---

Похожие калькуляторы:

Войдите чтобы писать комментарии

Рассчитайте результаты с двух сторон

Рассчитайте результаты с одной стороны и под одним углом

сделано с ❤️

Оглавление

Что такое прямоугольный треугольник?

Прямоугольный треугольник (американский английский) – это треугольник с одним прямым углом (90 °). Он также известен как прямоугольный треугольник (британский английский) или, более формально, ортогональный треугольник.

Пример прямоугольного треугольника

Что такое калькулятор треугольников?

Треугольники — одна из самых основных фигур в геометрии, и их часто используют для объяснения более сложных фигур. Используя калькулятор треугольников, вы можете легко рассчитать размеры треугольников и решить другие основные математические задачи. Этот простой инструмент может быть полезен, когда вы работаете над домашним заданием или пытаетесь понять более сложную проблему.

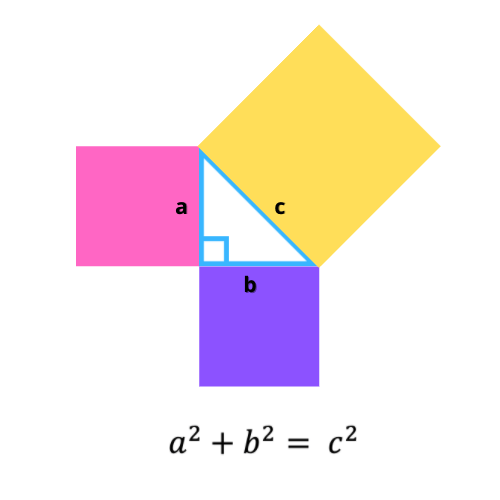
Теорема Пифагора

Теорема Пифагора, также известная как теорема Пифагора, связывает три стороны прямоугольного треугольника. Согласно этой формуле, площадь квадрата квадрата, сторона которого является гипотенузой треугольника, равна сумме площадей на двух других сторонах.

См. Визуальную демонстрацию ниже:

Теорема Пифагора – Википедия

Формулы прямоугольного треугольника

Прямоугольный треугольник содержит множество полезных формул. Вы можете использовать любую из приведенных ниже формул для вычисления углов, сторон, площади или периметра прямоугольного треугольника. Мы будем ссылаться на треугольник ниже для следующих формул:

Теорема Пифагора

Тригонометрические функции

Площадь треугольника

Периметр треугольника

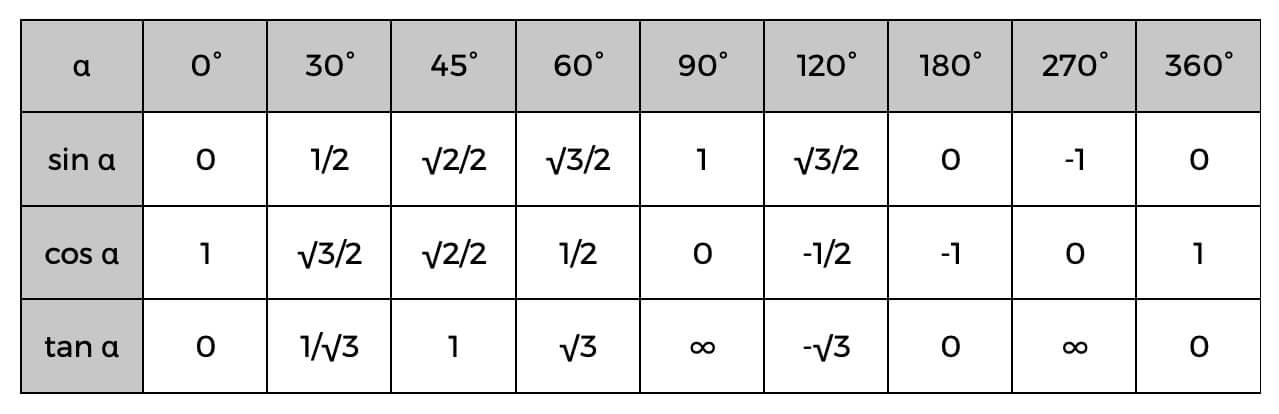
Также обратите внимание, что вам понадобится следующая таблица при использовании тригонометрических функций:

Например, если вы используете формулу tan B и рассчитываете, что ее значение равно 1, то, взглянув на таблицу выше, вы узнаете, что значение рассматриваемого угла должно быть 45 °.

Примеры прямоугольного треугольника из повседневной жизни

В прямоугольном треугольнике есть много важных и важных формул, которые используются в математике и в реальной жизни. Ниже вы увидите три наиболее важных использования прямоугольного треугольника:

1) Архитектура и инженерия

Не за горами подумать об использовании прямоугольного треугольника в архитектуре. В основном он используется для расчета длины диагонального соединения, соединяющего две линии. Это используется для расчета диагональной длины ската крыши при проектировании скатной крыши. Вам нужно будет знать только высоту и длину крыши, и все готово!

2) Электроника и электротехника

Правый треугольник используется для решения математических задач в электронике и электротехнике, в первую очередь при проектировании модели. Другой пример важности – внесение эстетических дополнений и обеспечение того, чтобы они не нарушали функцию модели.

Однако прямоугольный треугольник очень удобен при работе со схемами. См. Нижеприведенный наглядный пример для дальнейшей демонстрации и понимания того, как логика прямоугольного треугольника преобразуется в логику схемы.

3) Землеустройство (гражданское строительство)

Геодезия – это профессия, которая существует уже давно, по крайней мере, столько, сколько показывает история. Это делает геодезист, которому поручено точно измерить поверхность земли в большом масштабе. Вы, наверное, уже догадались об использовании прямоугольного треугольника; в основном, это происходит, когда геодезисту нужно вычислить длину, площади и относительные углы между объектами на ландшафте.

Пример ниже – отличный наглядный демонстратор того, что было объяснено ранее. Геодезист использует соответствующие формулы для расчета своего расстояния от вершины горы или любого другого места, которое он выберет.

См. Статью ниже для получения дополнительной информации о том, как работает съемка:

Геодезия – Википедия

Автор статьи

Parmis Kazemi

Пармис – создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.

Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) русский

Опубликовано: Tue Nov 02 2021

Последнее обновление: Fri Aug 12 2022

В категории Математические калькуляторы

Добавьте Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на свой сайт

Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на других языках

Как добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на мой сайт?

Вы можете легко добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!

Как добавить виджет Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на сайт WordPress?

Добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.

Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кодаLoading…