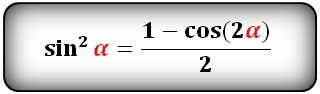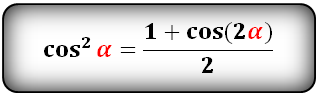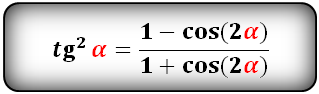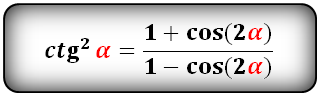Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза – сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза – это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс – «x», что не меняет сути).
Синус угла альфа (sin ∠α) – это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) – отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза – это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 – cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 – sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) < echo (Html::a(‘Войдите’, [‘/user/security/login’], [‘class’ =>”]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => ”]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(Yii::$app->user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))< $name = Yii::$app->user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else < $name = ”; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>–>
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
28.01.17 / 22:14, Иван ИвановичОтветить -2
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии “на пальцах”.
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sin | 0 | 1 | √3 | – | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ctg | – | √3 | 1 |
Принцип повтора знаков тригонометрических функцийУгол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Тригонометрический кругУглы в радианахДля математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Таблица СИНУСОВ для углов от 0° до 360° градусовСИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
Малая таблица значений тригонометрических функций (в радианах и градусах)
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
Полная таблица синусов для углов от 91° до 180°
Таблица синусов для углов 181° — 270°
Таблица синусов для углов от 271° до 360° Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе. Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать». Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла. Чему равен синус 45? … – А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071 [spoiler title=”источники:”] http://matematika.club/articles/trigonometry/ http://kvn201.com.ua/table-of-sines.htm [/spoiler] |
|
Как найти тангенс угла, если известен косинус? Как найти котангенс угла, если известен косинус?
Итак, читаем внимательно условие вопроса, и вспоминаем, чему нас учили в школе, у нас есть косинус угла, и этого окажется вполне достаточным для того, чтобы мы выполнили задание автора вопроса и нашли тангенс и котангенс данного угла. Вспоминаем, что мы можем найти, зная косинус, конечно-же, мы сразу можем найти синус, это очень легко, и в этом нам поможет вот это волшебное тождество и то, что из него следует, – формула для нахождения синуса: Теперь, зная чему равен синус угла, через косинус, проще простого решать дальше по известным формулам для нахождения тангенса и котангенса, просто подставляя в них эти формулы для синуса, которые я разместила выше: система выбрала этот ответ лучшим
Ксарфакс 5 лет назад Для того, чтобы найти тангенс и котангенс через косинус, достаточно вспомнить тригонометрические формулы: tgα = sinα / cosα. ctgα = cosα / sinα. Так как косинус известен, то синус можно найти из основного тригонометрического тождества: sin²α + cos²α = 1. sinα = √(1 – cos²α), если угол α находится в 1 и 2 четверти. sinα = – √(1 – cos²α), если угол α находится в 3 и 4 четверти. Таким образом: tgα = ± √(1 – cos²α) / cosα. ctgα = ± cosα / √(1 – cos²α). Так как произведение тангенса и котангенса = 1, то ctgα также можно найти из формулы: ctgα = 1 / tgα. Пример Косинус угла α равен 0,94, при этом α находится в 1 четверти (0 < α < 90). Нужно найти тангенс и котангенс. Воспользуемся формулой: tgα = √(1 – cos²α) / cosα. В первой четверти синус и косинус больше 0, поэтому тангенс и котангенс также будут положительными. tgα ≈ 0,34 / 0,94 ≈ 0,36. Соответственно ctgα ≈ 1 / 0,36 ≈ 2,78.
Лара Изюминка 6 месяцев назад В школе изучают следующую тригонометрическую формулу: Косинус в квадрате альфа равно единица разделить на сумму единицы и тангенса в квадрате альфа. Из этой формулы легко выразить тангенс в квадрате альфа. Он очевидно равен 1 деленная на косинус в квадрате альфа и из этой дроби нужно вычесть один, а можно еще преобразовать как на картинке. Ну, а для того чтобы выразить котангенс, нужно вспомнить , что произведение тангенса и котангенса равно единице, тогда просто меняем числитель и знаменатель местами и получается формула для нахождения котангенса через косинус. Ну, а знак тангенса и котангенса определяем по той четверти, в которой находится угол. Если это первая и третья четверти, то плюс, иначе минус.
bezdelnik 5 лет назад tg а = Sin a/Cos a. Чтобы выразить тангенс через косинус осталось выразить синус через косинус. Для этого воспользуемся основной тригонометрической формулой (Sin a)^2 +/(Cos a)^2 = 1. Тогда (Sin a)^2 = 1 – (Cos a)^2, Sin a = √(1 – (Cos a)^2), а tg = √(1 – (Cos a)^2)/Cos a. Например, при а= 60 градусов Cos 60° = 0,5, tg = √(1 – 0,25)/0,5 = √(0,75)/0,5 = √(3*0,25)/0,5 = (0,5*√3)/0,5 = √3 = 1,732… . ctg a = Cos a/Sin a, то-есть величина обратная tg а, и при а = 60° ctg 60° = 1/√3 = √3/3 = 0,57735… .
127771 3 года назад Первым делом стоит вспомнить определение тангенса и котангенса, а именно: То есть получаются следующие формулы: tg(x) = sin(x) / cos(x) ctg(x) = cos(x) / sin(x) Из условия задачи нам известен косинус, значит нам нужно будет найти синус. Для этого есть такая формула: sin^2(x) + cos^2(x) = 1 Значит: sin^2(x) = 1 – cos^2(x) sin(x) = √(1 – (Cos a)^2) Теперь у нас есть значения синуса и косинуса, которые можно будет подставить в следующие формулы:
Rafail 5 лет назад Наверное все помнят основное тождество тригонометрии: sin^2(x)+cos^2(x)=1. Почему-то также чётко я запомнил следующие простые формулы: tg^2(x)+1=sec^2(x) и ctg^2(x)+1=cosec^2(x). Ну и три определения: sec(x)=1/cos(x), cosec(x)=1/sin(x) и ctg(x)=1/tg(x). Теперь осталось выбрать нужные и применить. Допустим, cos(x)=(√3)/2, тогда sec(x)=2/√3, sec^2(x)=4/3, tg^2(x)=1/3, tg(x)=1/√3, ctg(x)=√3.
Зайцевана 5 лет назад Пусть cosa = 1/2, тогда tga^2 = 1/(cosa)^2-1, (tga)^2 =1/0,25 – 1 = 3, tga =корень квадратный из 3, (со знаком + или – в зависимости в какой четверти находится а). ctga = 1/корень из 3.
Синус, косинус, тангенс и котангенс угла – это тригонометрические функции. Можно сказать, что все они связаны между собой. Часто для нахождения одной из этих функций при условии, что известна другая, приходится вспоминать основные тригонометрические равенства или тождества, а также определение самих этих понятий. Зная все перечисленное выше, несложно выразить одну функцию через другую. Тангенс угла – это отношение синуса этого угла к его косинусу. Котангенс угла – это отношение косинуса угла к его синусу. Нам известен косинус, из основного тригонометрического тождества ( sin²α + cos²α = 1 ) выразим синус: sinα = √(1 – cos²α) для α из 1 и 2 четвертей, sinα = -√(1 – cos²α) для α из 3 и 4 четвертей. Подставив формулу для синуса угла в формулу тангенса и котангенса, получим формулы для вычисления значений этих функций: tgα = ± √(1 – cos²α) / cosα, ctgα = ± cosα / √(1 – cos²α). Котангенс, впрочем, можно вычислить путем попроще, вспомнив, что тангенс и котангенс – функции обратные, то есть ctgα = 1 / tgα. Подставляем в формулу значение тангенса и вычисляем котангенс.
Если вам требуется найти тангенс и котангенс при помощи косинуса, то вам предстоит воспользоваться определенной тригонометрической формулой:
при которой вы сможете отыскать синус из данной формулы, при том, что мы имеем известный косинус. Получившаяся формула выглядит таким образом:
Теперь, нам следует подставить значение синуса в формулу вычисления тангенса, а именно речь идет о : Теперь подставим аналогичную формулу через косинус для котангенса:
TheSun 3 года назад Для нахождения тангенса и котангенса через косинус необходимо воспользоваться приведенной ниже тригонометрической формулой: Находим синус из формулы указанной выше (при условии, что косинус нам известен), получается: Подставляем в формулу вычисления тангенса значение синуса: tg? = sin? / cos? = ± ?(1 – cos??) / cos?. Теперь аналогично для котангенса через косинус. ctg? = cos? / sin? = ± cos? / ?(1 – cos??).
Все функции мы знаем из курса тригонометрии, и в это же время проходят и алгоритм нахождения тангенса/котангенса через косинус. Ну как следует из вопроса косинус нам известен. Если нет, то находим по формулам – Имея на руках значения двух вводных – синуса и косинуса, далее еще проще действовать по формулам нахождения тангенса и котангенса. Знаете ответ? |
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Косинус в квадрате
Косинус (cos) — это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
cos 2 (x)=cos(x)*cos(x)
Значение косинуса находится в диапазоне от -1 до +1.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата косинуса (косинуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат косинус любого угла.
Квадрат синуса, косинуса, тангенса, котангенса (альфа)
квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
sin в квадрате
cos в квадрате
tg в квадрате
ctg в квадрате
Подробности Автор: Administrator Опубликовано: 17 сентября 2011 Обновлено: 13 августа 2021
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 февраля 2022 года; проверки требуют 16 правок.
Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения). В данной статье приведены только тождества с основными тригонометрическими функциями, но есть тождества и для редко используемых тригонометрических функций.
Пример шести тригонометрических функций угла θ = 0.7 радиан, построенный в единичной окружности. Величины, отмеченные 1, Sec(θ) и Csc(θ) равны длинам сегментов луча, исходящего из центра окружности. Величины Sin(θ), Tan(θ) и 1 равны высотам над осью
x, величины Cos(θ), 1 и Cot(θ) равны длинам сегментов оси
x от центра окружности.
Основные тригонометрические формулы[править | править код]
| № | Формула | Допустимые значения аргумента |
|---|---|---|
| 1.1 | 
|
 (то есть любое значение α)
|
| 1.2 | 
|
 при 
|
| 1.3 | 
|
|
| 1.4 | 
|
|
Формулы сложения и вычитания аргументов[править | править код]
Иллюстрация форм сложения и вычитания синусов и косинусов
Иллюстрация форм сложения тангенсов.
| № | Формулы сложения и вычитания аргументов |
|---|---|
| 2.1 | 
|
| 2.2 | 
|
| 2.3 | 
|
| 2.4 | 
|
Формула (2.3) получается при делении (2.1) на (2.2), а формула (2.4) — при делении (2.2) на (2.1).
Формула (2.3) верна при 
, 
, 
, отличных от 
, .
Вывод формул для 
Рис 1. К доказательству вывода формулы
На Рис. 1 изображены четыре прямоугольных треугольника: ABC, ABD, AOC, BOD.
Принято, что 
По построению: 
Тогда: 
Из треугольника ABD:
Из треугольника BOD:
Так как O лежит на отрезке AD:
Тогда сразу:
Из треугольника AOC:
Следовательно:
Что и требовалось доказать[источник не указан 2612 дней].
Формулы двойного угла и половинного угла[править | править код]
Формулы двойного угла выводятся из формул (2.1)—(2.4), если β приравнять α:
| № | Формулы двойного угла |
|---|---|
| 3.1 | 
|
| 3.2 |  
|
| 3.3 | 
|
| 3.4 | 
|
Из формулы двойного угла для косинуса (3.2) выводятся формулы половинного угла, в частности тангенса половинного угла:
| № | Формулы половинного угла |
|---|---|
| 3.5 | 
|
| 3.6 | 
|
| 3.7 | 
|
| 3.8 | 
|
В формулах половинного угла знаки перед радикалами следует брать в зависимости от знака тригонометрической функции, стоящей в левой части равенства.
В формуле 
и аналогичной для котангенса, левая и правая части имеют разные области определения и, следовательно, их неосторожное использование может приводить к приобретению корней!
Формулы тройного угла[править | править код]
Формулы тройного угла выводятся из формул (2.1)—(2.4), если β приравнять 2α:
| № | Формулы тройного угла |
|---|---|
| 4.1 | 
|
| 4.2 | 
|
| 4.3 | 
|
| 4.4 | 
|
Примечания
для формулы 
: 
для формулы 
: 
;
Формулы понижения степени[править | править код]
Формулы понижения степени выводятся из формул (3.2):
| № | Синус | № | Косинус | |
|---|---|---|---|---|
| 5.1 | 
|
5.5 | 
|
|
| 5.2 | 
|
5.6 | 
|
|
| 5.3 | 
|
5.7 | 
|
|
| 5.4 | 
|
5.8 | 
|
| № | Произведение |
|---|---|
| 5.9 | 
|
| 5.10 | 
|
| 5.11 | 
|
| 5.12 | 
|
Формулы преобразования произведения функций[править | править код]
| № | Формулы преобразования произведений функций |
|---|---|
| 6.1 | 
|
| 6.2 | 
|
| 6.3 | 
|
Вывод формул преобразования произведений функций
Формулы преобразования произведения функций выводятся из формул сложения аргументов (2.1) и (2.2).
Например, из формулы (2.1) следует:
- .
То есть:
- — формула (6.2).
Остальные формулы преобразования произведений функций выводятся аналогично.
Формулы преобразования суммы функций[править | править код]
| № | Формулы преобразования суммы функций |
|---|---|
| 7.1 | 
|
| 7.2 | 
|
| 7.3 | 
|
| 7.4 | 
|
| 7.5 | 
|
Вывод формул преобразования суммы функций
Формулы преобразования суммы функций выводятся из формул преобразования произведений функций (6.1)—(6.3) с помощью подстановки:
и
- .
Подставим эти выражения в формулу (6.1):
- , то есть
- — опуская штрихи, получаем формулу (7.3).
Остальные формулы преобразования суммы синуса и косинуса выводятся аналогично.
Из формулы (2.3) следует:
- , то есть
- — формула (7.4).
Преобразование суммы синусов 3-x разных углов в произведение при 
- (7.6).
Решение простых тригонометрических уравнений[править | править код]
-
- Если — вещественных решений нет.
- Если — решением является число вида где
- Если
-
- Если — вещественных решений нет.
- Если — решением является число вида
- Если
-
- Решением является число вида
- Решением является число вида
-
- Решением является число вида
- Решением является число вида
Универсальная тригонометрическая подстановка[править | править код]
Нижеприведённые тождества имеют смысл, только когда тангенс имеет смысл (то есть при 
).
Аналогичные соотношения имеют место и для котангенса (
):
Вспомогательный аргумент (формулы сложения гармонических колебаний)[править | править код]
Сумма двух гармонических колебаний с одинаковой частотой будет вновь гармоническим колебанием. В частности,
где 
и 
не равны нулю одновременно, 
— это угол, называемый вспомогательным аргументом, который может быть найден из системы уравнений:
Примечание. Из вышеприведённой системы при 
следует, что 
, однако нельзя всегда считать, что 
, так как арктангенс определяет угол от 
до 
, а угол может быть, вообще говоря, любым. Нужно учитывать знаки и 
чтобы определить, к какой четверти принадлежит угол , в результате чего добавлять или убавлять 
при необходимости.
Представление тригонометрических функций в комплексной форме[править | править код]
Формула Эйлера утверждает, что для любого вещественного числа 
выполнено следующее равенство:
где 
— основание натурального логарифма,
- — мнимая единица.
При помощи формулы Эйлера можно определить функции 
и 
следующим образом:
Отсюда следует, что
Все эти тождества аналитически обобщаются на любые комплексные значения.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Комплексные числа
- Многочлены Чебышёва
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Треугольник § Тригонометрические тождества только с углами
- Тригонометрические функции
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
как косинус может быть в квадрате это же не число? спасибо
Ученик
(68),
закрыт
14 лет назад
Куратор
Мудрец
(11377)
14 лет назад
Косинус – это конкретное числовое значение, которое характеризует конкретный угол. Косинус любого угла измеряется в пределах от (+1,0) до (-1,0). А число (чем косинус по сути и является) очень просто возвести не только в квадрат, но и в любую другую целую или дробную степень.
Если тебе скажут, что косинус угла составяет 1,2, а ты в это поверишь – получишь 2 (двойку) .
Помни, что сумма квадратов косинуса и синуса одного и того же угла всегда (!!!!) составляет единицу – не больше и не меньше !!!
Косинус (синус, тангенс, котангенс) – величины безразмерные, так как показывает отношение длин сторон треугольника, либо фигур, которые можно условно разделить на конечное число треугольников.
*
Знаток
(336)
14 лет назад
это число.. . =) например, косинус 30 градусов равен 1/2. так что он может быть и в квадрате, и под корнем, и как угодно.. . =)
