п.2.3.1.Отклонение электронного пучка в
однородном электрическом поле
электростатического конденсатора.
Наиболее простой является система в
виде плоского конденсатора. Пусть пучок
электронов запускается параллельно
пластинам (рис. 2.7 ), найдем угол отклонения
пучка в
зависимости от энергии частицWк0.
Поперечная скорость, приобретаемая в
отклоняющем электрическом поле:
,
где
–
время пролета отклоняющей системы, l– протяженность области действия поля.
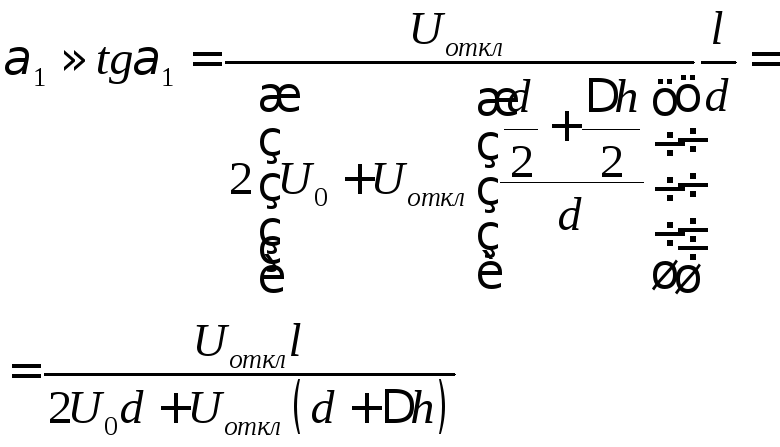
Тангенс угла вылета электрона:
,
где
-отклоняющее
напряжение, d–
расстояние между пластинами конденсатора.
Поперечное смещение электрона в пределах
отклоняющей системы:
,
следовательно, тангенс угла прямой,
соединяющей
|
Рис. |
центр системы с точкой вылета:
|
,
Поперечное смещение на расстоянииxот центра системы определяется
.
п.2.3.2. Фокусировка электронного пучка
в однородном электрическом поле
электростатического конденсатора.
В поле плоского конденсатора можно не
только отклонять, но и фокусировать
пучки заряженных частиц. Благодаря
различным значениям потенциала на
верхней и нижней границе пучка (рис.2.8),
а значит и различным скоростям частиц,
происходит фокусировка пучка. Такие
системы используются в электронно-лучевых
экранах. Можно оценить фокусное расстояние
(расстояние от центра системы до точки
фокусировки). Распределение потенциала
в отклоняющей системе:
.
Тогда потенциал в точках А и В:
,
.
Для малых углов отклонения:
|
Рис.
|
|
.
.
Разность углов отклонения частиц на
границах пучка:
.
Тогда фокусное расстояние можно оценить
соотношением:
. Таким образом, с ростом угла отклонения
уменьшается расстояние до точки
фокусировки, это является причиной
выпуклости экранов.
п.2.3.3.Отклонение в однородном магнитном
поле, ограниченном в пространстве.
|
Рис. |
поле
|
,
.
,
.Рассмотрим систему, в которой
поперечное к движению пучка однородное
магнитное поле существует в ограниченном
пространстве протяженности
(рис.2.9). Магнитное
п.2.3.4.Фокусировка пучка в продольном
однородном магнитном поле.
В
Рис. 2.10. Фокусировка
в однородном продольном магнитном
поле.
продольном однородном магнитном поле
фокусировка происходит в силу того, что
вышедшие из одной точки частицы после
совершения одного оборота по ларморовской
окружности возвращаются на исходную
силовую линию магнитного поля (рис.
2.10). Проекция движения частиц на
перпендикулярную к силовым линиям
плоскость представляет собой пучок
окружностей, имеющих общую точку. Если
угол расходимости пучка
невелик, то фокусировка моноэнергетического
пучка произойдет через один оборот на
расстоянииl=tлVcos2mVc/(eH),
гдеtл=
2mc/(eH)
– период вращения по ларморовской
окружности. Таким образом, расстояние
до места фокусировки пучка зависит от
скорости и массы частиц, и продольное
однородное магнитное поле может быть
использовано для энерго- и масс-сепарации
частиц.
п.2.3.5.Фокусировка пучка в поперечном
однородном магнитном поле энергоанализатора
или массепаратора.
Благодаря зависимости радиуса вращения
в магнитном поле от поперечной скорости
Vи массыmзаряженной
частицы, возможно их разделение
(сепарация) по энергиям и массам, а также
фокусировка как в поперечном, так и в
продольном однородном магнитном поле.
В поперечном магнитном поле наиболее
распространенной является схема с
полукруговой фокусировкой (рис. 2.11).
Выходящий из точечного источникаАперпендикулярно силовым линиям пучок
моноэнергетических частиц будет
фокусироваться после полуоборота на
расстоянии
.
Фокусировка частиц, вылетевших под
одинаковым угломк центральной траектории пучка, происходит
благодаря тому, что круговые траектории
частиц имеют одинаковые радиусы, и их
|
Е
Рис. |
траектории опираются на диаметры,
где
|
,
,
Ширина щели, необходимая для прохождения
.
Если известна масса и заряд – можно
определить энергию (энергоанализатор):
.
Если известна энергия и заряд – можно
определить массу (масс-сепаратора):
.
Если известна масса и энергия – можно
определить заряд (зарядоанализатор):
.
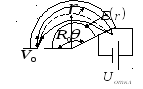
п.2.3.6. Отклонение и фокусировка ионного
пучка в неоднородном электрическом
поле цилиндрического конденсатора
(энергоанализатор).
Хорошую фокусировку позволяет
получить цилиндрический конденсатор.
Электрическое поле цилиндрического
конденсатора обратно пропорционально
расстоянию от центра системы, E(r)
=c/r,
та как по теорема Гаусса поток
электрического поля равен заряду:
,
то есть,
.
Следовательно, уравнение для потенциала
,
тогда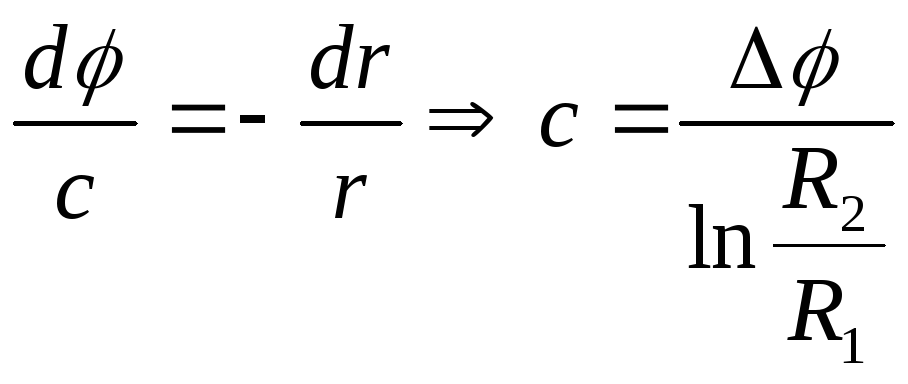
,
где
– радиусы цилиндров (рис.2.12). Таким
образом, электрическое поле в цилиндрическом
конденсаторе:
,
где
=U2–U1,U1,U2
– потенциалы внутреннего и
|
Рис. |
внешнего |
|
Рис. |
Для решения уравнения движения для |
(остальные попадут на стенки цилиндра),
.
и угловое ускорение
.
.
.Для нецентральной траектории уравнение
движения:
.
Исходя из равенства потока электрического
поля
.
Удобно рассмотреть отклонение траектории
от круговой:
(r <<R).
Тогда уравнение движения можно
представить в виде:
.
С учетом постоянства в поле центральных
сил секторальной скорости
выполняется соотношение
,
тогда получим уравнеие:
.
Приведем его к виду: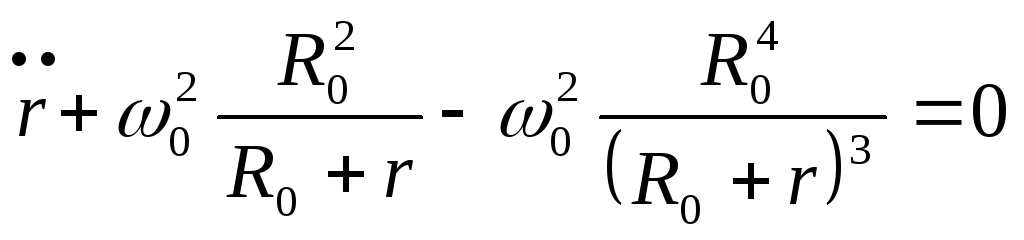
или
,
в результате преобразований получим
уравнение:
.
Пренебрегая
и
,
имеем гармонические колебания:
,
решение которого представляет собой
колебания около круговой траектории с
полупериодом
,
то есть после поворота на этот угол
пучок фокусируется на круговой траектории
(фокусировка по Юзу и Рожанскому).
Соседние файлы в папке Lekcii
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Отклонение пучка электронов может быть вызвано с помощью отклоняющих систем. Основное назначение отклоняющих систем состоит в пространственном перемещении сфокусированного электронного луча. Есть два принципиально различных типа отклоняющих систем: электростатическая, в которой отклонение электронного луча осуществляется поперечным (по отношению к вектору скорости электронов) электрическим полем, и магнитная, использующая поперечное магнитное поле. Отклоняющие системы должны обладать хорошей чувствительностью и малыми искажениями сигналов.Если требуется перемещать луч последовательно по всей плоскости экрана, то простейшая электростатическая отклоняющая система состоит из двух пар попарно ортогональных пластин, расположенных последовательно вдоль оси трубки. Одна пара пластин отклоняет луч в вертикальном направлении, другая –
в горизонтальном. Рассмотрим движение электронов между парой полубесконечных плоских пластин под действием поля ε, создаваемого разностью потенциалов, приложенной к пластинам.
Уравнения движения нерелятивистских электронов в декартовой системе координат при наличии только поперечного электрического поля ε=-εz (εx=εy=0) (рис. 9.6) можно записать в форме:
; (9.3)
; (9.4)
. (9.5)
Допустим, что электрон влетает в пространство между пластинами в направлении оси х с начальной скоростью νx0 (νy=0, νz0=0). Интегрируя (9.3) — (9.5), получаем следующий результат:
; 
; 
. (9.6)
Определяя из первого уравнения (9.6) t и подставляя этот результат во второе, получаем:
. (9.7)
Таким образом, согласно (9.7) траекторией движения электрона в однородном электростатическом поле плоских пластин является парабола. Электроны на выходе из пластин длиной l1 отклоняются на величину
. (9.8)
где ε=Uпл/d; Uпл, d – соответственно разность потенциалов и расстояние между пластинами, 
Ua2— напряжение на втором аноде, определяющее скорость на входе в пластины v0x.
Угол отклонения траектории электрона от первоначального направления определяется дифференцированием (9.7) по х:
, x=l1 (9.9)
Перейдем теперь к вычислению траектории электронов при движении их в магнитной отклоняющей системе, которая обычно содержит две пары катушек, надеваемых на горловину трубки и образующих магнитные поля во взаимно перпендикулярных направлениях. Аналогично электростатической отклоняющей системе, одна из пар катушек отклоняет луч в вертикальной, а другая — в горизонтальной плоскости. Рассмотрим отклонение электрона однородным магнитным полем одной пары катушек (рис. 9.7). В однородном магнитном поле (В= Вy Вx= Вz= 0) (при полном отсутствии электрического) уравнения движения электронов в декартовой системе координат имеют вид:
(9.10)
Система уравнений (9.10) справедлива для вычисления траектории электронов как в магнитных отклоняющих, так и в фокусирующих системах. Из (9.10) видно, что сила, действующая на электроны, перпендикулярна V, т.е. полная скорость электрона 
является величиной постоянной, а направление движения электрона изменяется. Если принять, что x0=0, vz0=0, vx0=v0, то решение системы (9.10) можно записать в форме
(9.11)
где 
– циклотронная частота. Уравнения (9.11) описывают траекторию движения электрона в однородном магнитном поле, которая представляет собой окружность радиуса 
. Следовательно, в однородном магнитном поле электрон будет вращаться по окружности радиуса R с частотой 
. Поскольку диаметр l1 отклоняющих катушек, как правило, существенно меньше R, на выходе из них электрон отклонится от оси трубки на некоторую величину z=l1tg(α) (см. рис, 9.7) и дальше будет двигаться по касательной к его криволинейной траектории в точке выхода из поля. При малых углах tg α = α. и тогда 
, если принять, что путь, пройденный внутри катушек, незначительно превышает их диаметр, то
(9.12)
где Ua — потенциал последнего электрода перед отклоняющей системой. Угол α нетрудно вычислить и из (9.12). Как известно, индукция магнитного поля пропорциональна числу ампер-витков, т.е. B=k1ωI (k1— коэффициент пропорциональности, определяемый конструкцией катушки; ω — число витков: I — ток, протекающий по виткам).
Полное смещение h электрона на плоском экране ЭЛТ, отстоящем на расстоянии L от центра отклоняющих систем (см. рис. 9.6 и 9.7), равно h=tg α. Используя (9.8) и (9.12), можно вычислить смещение луча для электростатической и и магнитной систем отклонения:
(9.13)
(9.14)
соответственно характеризуют отклонение луча или при развости потенциалов между отклоняющими пластинами в 1 В, или при изменении тока, протекающего через катушки, на 1 А. 
измеряется в мм/В, а — в мм/А. Из (9.14) видно. что при магнитном отклонении изменение ускоряющего напряжения Ua существенно меньше влияет на чувствительность, чем при электростатическом, так как 
.
К достоинствам магнитного отклонения можно отнести меньшие аберрации, внешнее относительно ЭЛТ расположение катушек, что позволяет применять отклоняющие системы, вращающиеся вокруг оси трубки. Среди существенных недостатков магнитных отклоняющих систем — значительно большие потребляемые мощности, а также большая инерционность вследствие значительных собственных емкостей и индуктианостей. Электростатические отклоняющие системы из-за малых значений паразитных емкостей и малых времен пролета электронов могут работать на частотах до нескольких сотен мегагерц, а магнитные — только до нескольких десятков килогерц.
Электростатические отклоняющие пластины располагаются в пространстве последовательно друг за другом. Совмещение вертикальных и горизонтальных отклоняющих систем нерационально из-за их сильного взаимного влияния, приводящего к большим искажениям при отклонении луча. Вертикальные и горизонтальные магнитные отклоняющие катушки обычно совмещают в пространстве, так как их взаимное влияние нетрудно исключить точной установкой и изготовлением.
В электростатических системах для увеличения максимального угла отклонения чувствительности и уменьшения искажения при отклонении луча применяют косо расставленные, изломанные и изогнутые пластины. Наилучшие результаты получаются в случае применения изогнутых пластин, при которых траектория электронов луча эквидистантна поверхности отклоняющей системы.
Макеты страниц
Рассмотрим узкий пучок одинаковых заряженных частиц (например, электронов), попадающий в отсутствие полей на перпендикулярный к нему экран в точке О (рис. 73.1). Определим смещение следа пучка, вызываемое перпендикулярным к пучку однородным электрическим полем, действующим на пути длиной 
Пусть первоначально скорость частиц равна 
Войдя в область поля, каждая частица будет двигаться с постоянным по величине и направлению, перпендикулярным к 
ускорением 
— удельный заряд частицы).
Рис. 73.1.
Движение под действием поля продолжается время 
За это время частицы сместятся на расстояние
и приобретут перпендикулярную к 
составляющую скорости
В дальнейшем частицы летят прямолинейно в направлении, которое образует с вектором 
угол а, определяемый соотношением
В результате в дополнение к смещению (73.1) пучок получает смещение
где 
— расстояние от границы области, в которой имеется поле, до экрана.
Таким образом, смешение следа пучка относительно точки О равно
Приняв во внимание формулу (73.2), выражению для смещения можно придать вид
Отсюда вытекает, что частицы, покинув поле, летят так, как если бы они вылетели из центра конденсатора, создающего поле, под углом а, который определяется формулой (73.2).
Теперь предположим, что на имеющей протяженность Л пути частиц включается перпендикулярное к их скорости 
однородное магнитное поле (рис. 73.2; поле перпендикулярно к плоскости рисунка, область поля обведена пунктирной окружностью). Под действием поля каждая частица получит постоянное по величине ускорение 
Рис. 73.2.
Ограничиваясь случаем, когда отклонение пучка полем невелико, можно считать, что ускорение 
постоянно по направлению и перпендикулярно к 
. Тогда для расчета смещения можно использовать полученные нами формулы, заменив в них ускорение 
значением 
. В результате для смещения, которое мы теперь обозначим буквой 
получится выражение
Угол, на который отклонится пучок магнитным полем, определяется соотношением
С учетом (73.5) формулу (73.4) можно представить в виде
Следовательно, при небольших отклонениях частицы, покинув магнитное поле, летят так, как если бы они вылетели из центра области, в которой имеется отклоняющее поле, под углом р, величина которого определяется выражением (73.5).
Из формул (73.3) и (73.4) видно, что как отклонение электрическим, так и отклонение магнитным полем пропорционально удельному заряду частиц.
Отклонение пучка электронов электрическим или магнитным полем используется в электронно-лучевых трубках. Внутри трубки с электрическим отклонением (рис. 73.3), кроме так называемого электронного прожектора, создающего узкий пучок быстрых электронов (электронный луч), помещаются две пары взаимно перпендикулярных отклоняющих пластин. Подавая напряжение на любую пару пластин, можно вызвать пропорциональное ему смещение электронного луча в направлении, перпендикулярном к данным пластинам. Экран трубки покрывают флуоресцирующим составом. Поэтому в месте попадания на экран электронного луча возникает ярко светящееся пятно.
Рис. 73.3.
Электронно-лучевые трубки применяются в осциллографах — приборах, позволяющих изучать быстропротекающие процессы. На одну пару отклоняющих пластин подают напряжение, изменяющееся со временем линейно (напряжение развертки), на другую — исследуемое напряжение. Вследствие ничтожной инерционности электронного луча его отклонение практически без запаздывания следует за изменениями напряжений на обеих парах отклоняющих пластин, причем луч вычерчивает на экране осциллографа график зависимости исследуемого напряжения от времени. Многие неэлектрические величины могут быть с помощью соответствующих устройств (датчиков) преобразованы в электрические напряжения. Поэтому с помощью осциллографов исследуют самые различные процессы.
Электронно-лучевая трубка является неотъемлемой частью телевизионных устройств. В телевидении чаще применяются трубки с магнитным управлением электронным лучом. У таких трубок вместо отклоняющих пластин имеются две расположенные снаружи взаимно перпендикулярные системы катушек, каждая из которых создает перпендикулярное к лучу магнитное поле. Изменяя ток в катушках, вызывают перемещение светового пятна, создаваемого электронным лучом на экране.
В предыдущем ответе не учёл то обстоятельство, что угол между вектором скорости частицы и вектором магнитной индукции всё время меняется при отклонении частицы, поэтому нельзя пренебрегать синусом угла между ними..
Итак, разложим вектор скорости частицы на две координатные оси: одна вдоль вектора магнитной индукции (У), другая (х) – вдоль вдоль начальной траектории частицы, эти координатные оси взаимно перпендикулярны..
Скорость вдоль х неизменна и её можно найти из энергетического соотношения:
mv^2/2=qU
Откуда v(х)=sqrt(2qU/m)
Путь, пройденный вдоль оси у равен: L=v(x)t
Или t=L/v(x)
Скорость вдоль у перед влётом в магнитное поле равна нулю и определяется всецело силой Лоренца:
F=qvB sin(alpha)
Путь, пройденный вдоль оси у равен:
S=(F/m)(t^2)=(qvB/m) sin(alpha)(t^2)=(qvB/m) sin(alpha)(mL)/(2qU/m)
Таким образом получается поперечное смещение:
S=sqrt(q/(2mU))B(L)^2 sin (alpha)
Отношение поперечного смещения к продольному есть тангенс искомого угла:
tg(alpha)=S/L=sqrt(q/(2mU))B L sin (alpha)
Далее учитываем, что tg(a)=sin(a)/cos(a)
cos(alpha)= 1/(sqrt(q/(2mU))B L)
или окончательно:
alpha= arccos(1/(sqrt(q/(2mU))B L))
подставляем значения
m=1,67×10^(-27)кг
q=1,6×10^(-19)Кл
B=50×10^(-3)Тл
U=1200В
L=0,1м
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
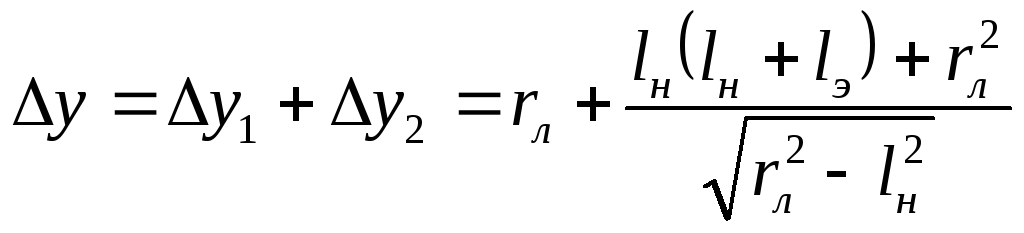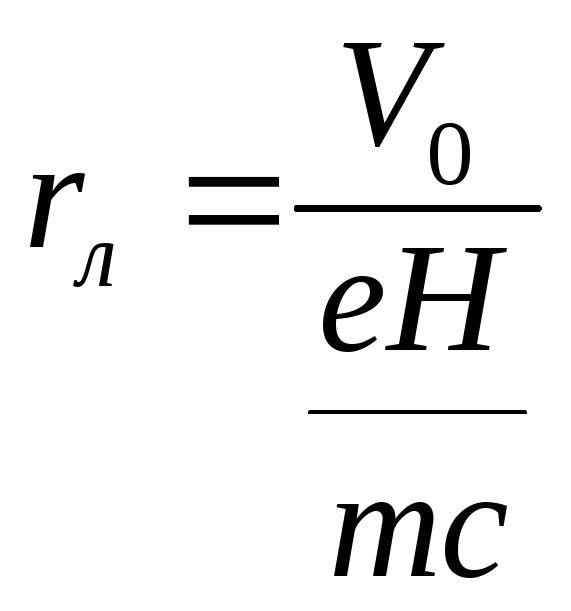