
Пример решения задачи по определению угла отклонения стержня от вертикали при его вращении как функцию угловой скорости и реакций опор в заданных точках.
Задача
С невесомым валом AB шарнирно скреплен однородный стержень OD длиной l и массой m1, имеющий на конце груз массой m2.
Вал и стержень вращаются вокруг оси OZ с постоянной угловой скоростью ω. Известны b1 и b2 – расстояния от опор до точки крепления стержня (рисунок 1.4).
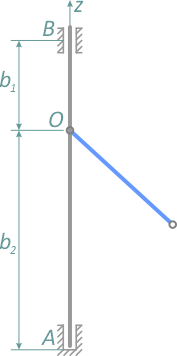
Рисунок 1.4
Требуется определить угол отклонения стержня от вертикали — α, как функцию угловой скорости и реакции опор A и B.
Другие примеры решений >
Помощь с решением задач >
Решение
Применим принцип Даламбера для данной системы. Проведем вращающиеся вместе с валом и стержнем оси координат Axyz так, чтобы стержень OD находился в плоскости yAz. Внешние силы: G1, G2; реакции опор: xA, yA, zA, xB, yB; силы инерции Φ1 и Φ2 (рисунок 1.5).
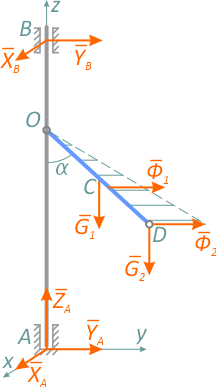
Рисунок 1.5
Отклонение стержня от вертикали происходит за счет сил инерции. Определенной угловой скорости соответствует свой угол отклонения. Величина силы инерции стержня определяется из формулы
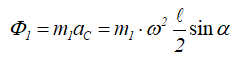
и направлена перпендикулярно к оси вращения, в сторону, противоположную ускорению центра масс стержня.
Эпюра распределения сил инерции стержня представляет собой треугольник (элементарные силы инерции частичек стержня возрастают с удалением от точки O к точке D, т.к. растет их ускорение с увеличением радиуса вращения). Результирующая таких сил приложена на расстоянии 2/3 длины стержня от точки O (см. раздел «Статика», распределенные нагрузки).
Сила инерции точечной массы
![]()
Напишем для равновесия стержня при данной угловой скорости ω уравнение моментов относительно точки O – точки крепления стержня:
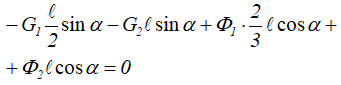
подставляем данные:
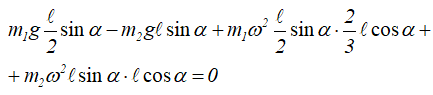
определяем угол:
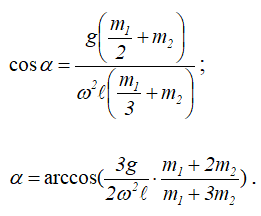
Для определения реакций опор вала составим уравнения равновесия:
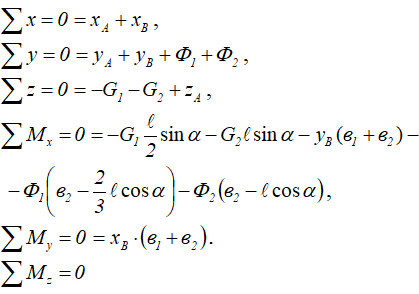
— вращающие моменты отсутствуют, система вращается по инерции, с постоянной угловой скоростью.
Из имеющихся пяти уравнений, подставляя данные задачи, можно найти пять неизвестных реакций в опорах A и B.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
2017-05-21 ![]()
В вагоне, движущемся горизонтально с ускорением $a = 2 м/с^{2}$, висит на шнуре груз массы $m = 200 г$. Найти силу натяжения шнура и угол отклонения шнура от вертикали (рис.).

Решение:
В задаче рассматривается движение тела, ни о форме которого, ни о линейных размерах ничего не сказано. Это позволяет предположить, что и форма и линейные размеры не влияют на характер движения, а тело можно принять за материальную точку.
Независимо от состояния вагона (покой или движение) на груз действуют только две силы: сила тяжести $m vec{g}$ и сила натяжения $vec{T}$ шнура. В покоящемся вагоне (или в случае его движения с постоянной скоростью) обе силы коллинеарны, и их векторная сумма равна нулю. При движении вагона с ускорением шнур отклонится от вертикали в сторону, противоположную направлению ускорения, и обе действующие на груз силы должны сообщать грузу относительно Земли ускорение, равное ускорению вагона. Правильнее было бы говорить, что и груз отклоняется, а вагон, и, следовательно, точка подвеса шнура к вагону опережает груз. (В начале движения вагона с ускорением груз совершает колебания. Мы рассматриваем груз в тот момент, когда колебания затухнут, т. е. когда ускорение и скорость груза равны ускорению и скорости вагона. Нить при этом оказывается отклоненной от вертикали.) Поскольку вагон движется по отношению к Земле с ускорением, следует выбрать систему координат, не связанную с движущимся вагоном. В системе координат, жестко связанной с Землей, второй закон Ньютона имеет вид
$m vec{a} = m vec{g} + vec{T}$, (1)
где $vec{a}$ – ускорение груза относительно Земли, а $vec{T}$ — искомая сила натяжения.
Заменяя уравнение (1) двумя скалярными равенствами, связывающими между собой проекции сил и ускорения на оси ОХ и OY, получаем:
$ma = T sin alpha$, (2)
$0 = T cos alpha – mg$. (3)
Совместно решив эти два уравнения, найдем:
$alpha = arctg (a/g) = arctg 0,204 = 11,5^{ circ}$;
$T = m sqrt{a^{2} + g^{2}} = 20 H$.
Отклонение – груз
Cтраница 1
Отклонение груза от положения равновесия обозначим через у.
[1]
Наибольшие радиальные и тангенциальные составляющие отклонений груза примерно равны, но во времени они не совпадают.
[2]
Угол отклонения груза от вертикали а может также рассматриваться как результат косого подъема груза.
[3]
Датчик измеряет отклонение груза 2 от вертикали и выдает в цепь якоря 4 напряжение, пропорциональное угловой скорости маятника, U / мер. Индуктивность цепи якоря равна L, масса груза т, расстояние от оси вращения статора до центра масс груза 0С /, момент инерции якоря относительно оси вращения J, момент на якоре Мя / c2i, где / с2 – – – const, i – ток в обмотке якоря.
[4]
Расчетные углы отклонения груза от вертикали у поворотных кранов приведены в разд.
[5]
Из табл. 45 видно, что величина отклонения груза зависит от скорости ветра, площади наветренной поверхности и высоты подъема груза.
[6]
Такая ситуация возникает, например, при отклонении груза, прикрепленного к середине недеформированной пружины с закрепленными концами, в перпендикулярном пружине направлении. Размерность 7 в этом случае м – 2с – 2, и период колебаний Т – 1 А-1 обратно пропорционален амплитуде.
[7]
Система имеет одну степень свободы: qx – отклонение груза от положения покоя.
[8]
Подчеркнем, что данное выражение справедливо как при отклонении груза влево, когда потенциальная энергия – это энергия груза в поле тяжести, так и при отклонении вправо, когда потенциальная энергия системы складывается из энергии груза в поле тяжести и потенциальной энергии растянутой резинки.
[9]
Подчеркнем, что данное выражение справедливо как при отклонении груза влево, когда потенциальная энергия – это энергия груза в поле тяжести, так и при отклонении вправо, когда потенциальная энергия системы складывается из энергии груза в поле тяжести и потенциальной энергии растянутой резинки.
[10]
Если в момент г я / О12, когда отклонение груза максимально, увеличить момент Мдан вдвое, уменьшение отклонения груза не произойдет и колебания прекратятся.
[12]
Для определения динамической нагрузки на ГУ, возникающей при отклонении груза по дуге, можно применить формулы, выведенные при рассмотрении влияния на L этот процесс передвижения крана.
[13]
При увеличении v и k продолжительность этого этапа и величина отклонения груза из положения равновесия уменьшаются. Как уже указывалось, этап равномерного движения при относительном покое соприкасающихся элементов в точке срыва сменяется неравномерным относительным движением этих элементов, обусловленным силами упругости пружины и силой трения скольжения, которая изменяется с увеличением скорости относительного движения.
[14]
При подъеме на высоту, превышающую 30 м, величина отклонения груза значительно увеличивается.
[15]
Страницы:
1
2
3
4
Подвешенному на нити шарику сообщили начальную скорость в горизонтальном направлении. Когда нить отклонилась на угол α = 30° от вертикали, ускорение шарика оказалось направленным горизонтально. Найдите угол максимального отклонения нити.
Решение:
Когда нить отклонена на угол α, составляющие ускорения, направленные вдоль нити и по касательной к траектории шарика, определяются формулами:
где v — скорость шарика, l — длина нити.
Поскольку ускорение шарика в этот момент направлено горизонтально, проекции векторов an и aτ на вертикальную ось одинаковы по модулю:
или
откуда:
Далее запишем закон сохранения энергии для шарика:
| mv2 | + mgl • (1 − cos α) = mgl •(1 − cos αm). |
| 2 |
Решая это уравнение относительно cos αm, получим:
| cos αm = cos α − | v2 | = cos α − | sin2 α | = 0,73. |
| 2gl | 2 cos α |
Далее: дробинка во льду тонет [тема: задачи на минимум и максимум]
Теги:
- задачи с решениями
- механика
- законы сохранения
- закон сохранения энергии
2010-03-24 22:33
Иная картина получается при сравнении данного движения относительно какой-либо инерциальной и какой-либо неинерциальной систем отсчета. Силы, действующие, на тело со стороны других тел: силы упругости, трения, тяготения и т. д., не зависят от того, по отношению к какой системе отсчета изучается движение тела. Но ускорения тел относительно инерциальной и неинерциальной систем различны. Поэтому по отношению к неинерциальным системам отсчета нельзя будет объяснить данное движение тела силами, действующими на него со стороны каких-то определенных других тел.
Проиллюстрируем это снова на примере подвешенного груза, считая теперь, что вагон, принимаемый за систему отсчета, движется по горизонтальному прямому участку пути ускоренно. Ускорение поезда обозначим через
![]()
. В этом случае нить, на которой подвешено тело, установится при равновесии не по отвесу, как в равномерно движущемся вагоне, а под некоторым углом к вертикали, отклоняясь в сторону, противоположную ускорению вагона (рис. 205). Отклонение тем больше, чем больше ускорение. Таким образом, тело относительно вагона находится в равновесии, в то время как силы, действующие на тело (сила тяжести
![]()
и сила натяжения нити
![]()
), направлены под углом друг к другу и поэтому уравновешивать друг друга не могут: тело покоится относительно системы отсчета, в то время как результирующая действующих на него сил не равна нулю. Эту результирующую силу легко найти, рассмотрев движение тела относительно Земли. Так как тело относительно вагона неподвижно, то его ускорение
![]()
относительно Земли равно ускорению вагона
![]()
(т. е.
![]()
). Следовательно, результирующая сила равна
![]()
и направлена горизонтально (рис. 205).
Если нить, на которой висит тело, пережечь, то оно начнет ускоренно падать, причем, как показывает опыт, его траектория относительно вагона окажется наклонной прямой, лежащей на продолжении нити до того, как она была пережжена (рис. 205). Но после пережигания нити на тело действует только одна сила — сила притяжения Земли, направленная вертикально вниз. Ускорение же относительно вагона направлено под углом к вертикали.

Рис. 205. Отклонение отвеса в ускоренно движущемся вагоне
Что же касается движения тела относительно Земли, то оно легко объясняется действующими силами: до пережигания нити равнодействующая сил, действующих на тело, равнялась та, поэтому тело и двигалось с тем же ускорением, что и поезд; после пережигания нити тело падает по параболе с начальной скоростью, равной скорости поезда в момент пережигания нити; действительно, после того как нить пережжена, движение поезда уже никак не влияет на движение не связанного с ним тела.
128.1.
Найдите угол
![]()
отклонения от вертикали нити с подвешенным на ней грузом массы
![]()
в вагоне, движущемся по горизонтальному пути с ускорением
![]()
. Зависит ли этот угол от массы груза? Найдите силу натяжения нити
![]()
.
128.2.
Какая сила должна действовать на тело массы
![]()
, чтобы оно двигалось равномерно и прямолинейно относительно вагона, движущегося поступательно с ускорением
![]()
?
