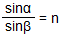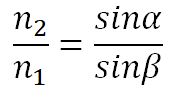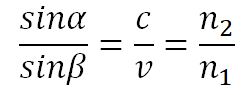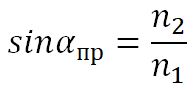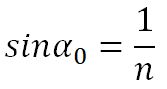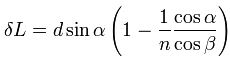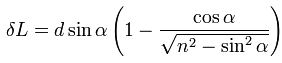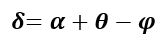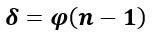Условие задачи:
Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°. Угол падения луча на грань призмы равен 30°, а показатель преломления вещества призмы равен 1,5.
Задача №10.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(varphi=60^circ), (alpha=30^circ), (n_1=1,5), (theta-?)
Решение задачи:
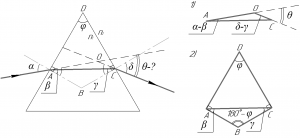 Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Рассмотрим треугольник AOC (смотрите рисунок 1). Искомый угол (theta) является смежным для этого треугольника, поэтому справедливо:
[theta = left( {alpha – beta } right) + left( {delta – gamma } right)]
[theta = alpha + delta – left( {beta + gamma } right);;;;(1)]
Далее рассмотрим четырёхугольник ABCD (смотрите рисунок 2). В этом четырехугольнике два угла – прямые, поэтому угол ABC равен (left( {180^circ – varphi } right)). На этом рисунке теперь рассмотрим треугольник ABC. Сумма углов любого треугольника равна 180°, поэтому будет верно записать:
[beta + gamma + left( {180^circ – varphi } right) = 180^circ ]
[varphi = beta + gamma ;;;;(2)]
Тогда уравнение (1) примет вид:
[theta = alpha + delta – varphi ;;;;(3)]
Чтобы найти угол преломления (delta), запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin gamma = {n_2}sin delta ]
Здесь (gamma) и (delta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_2) равен 1. Тогда:
[sin delta = frac{{{n_1}sin gamma }}{{{n_2}}}]
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin gamma } right)]
Из равенства (2) также следует, что (gamma = varphi – beta), поэтому:
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – beta } right)} right);;;;(4)]
Чтобы найти угол преломления (beta), опять запишем закон преломления света:
[{n_2}sin alpha = {n_1}sin beta ]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Тогда:
[sin beta = frac{{{n_2}sin alpha }}{{{n_1}}}]
[beta = arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)]
Полученное выражение подставим в (4):
[theta = alpha – varphi + arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)} right)} right)]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[theta = 30^circ – 60^circ + arcsin left( {frac{{1,5}}{1}sin left( {60^circ – arcsin left( {frac{{1 cdot sin 30^circ }}{{1,5}}} right)} right)} right) = 47,1^circ ]
Ответ: 47,1°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.37 Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает
10.3.39 Луч света входит в стеклянную призму под углом π/6 и выходит из призмы в воздух
10.3.40 Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды
|
17:22 Найти угол отклонения нормально падающего луча призмой |
|
Задача. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определить угол отклонения φ луча призмой, если ее преломляющий угол А = 30°. Решение задачи по физике: Для решения данной задачи по геометрической оптике воспользуемся законом преломления света: Закон преломления светаПреломление света — явление, при котором луч света, переходя из одной среды в другую, изменяет направление на границе этих сред. Преломление света происходит по следующему закону: При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Рисунок для решения нашей задачи по физике имеет вид $$frac{sinalpha }{sinbeta }=n$$ Отсюда получаем, что $$sinalpha =nsinbeta Rightarrow alpha =arcsinleft ( nsinbeta right )$$ Из геометрии рисунка видно, что $$beta =A,varphi =alpha -beta =alpha -A$$ Подставляем значения и находим: $$alpha =arcsinleft ( nsinbeta right ) =arcsinleft ( 1.5sin30 right )=48.59^{circ}$$ Угол отклонения луча призмой будет равен: $$varphi =alpha -A=48.59-30=18.59^{circ}=18^{circ}36{}’$$ |
Категория: Решение задач по физике | Просмотров: 15264 | | Теги: геометрическая оптика, нормадьно подает луч, грань стеклянной призмы, закон преломления света | Рейтинг: 3.4/7 |
11
3.1. Определение показателя преломления веществ по углу наименьшего отклонения
Рассмотрим метод
определения показателя преломления,
применимый для прозрачных веществ.
Метод состоит в измерении угла отклонения
лучей при прохождении света через
призму, изготовленную из исследуемого
материала. На призму направляется
параллельный пучок лучей, поэтому
достаточно рассмотреть ход одного из
них (S1)
в плоскости, перпендикулярной линии
пересечения
луча преломляющих
граней призмы (рис.6).
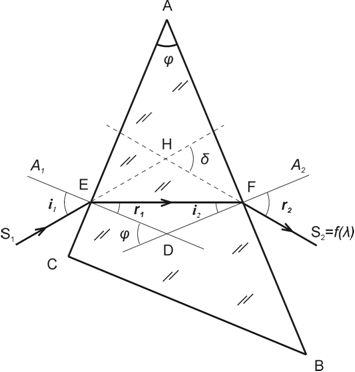
Рис.6.
S1─направление
луча, падающего на призму,
S2─
направление луча, вышедшего из призмы,
А1─направление
нормали к грани, на которую падает луч
S1,
А2─
направление нормали к грани, из которой
выходит луч S2,
i1,
i2
– углы падения,
r1,
r2
– углы преломления на границах раздела
АС и АВ
соответственно,
φ
– преломляющий угол призмы,
δ
– угол отклонения выходящего из призмы
луча относительно первоначального
направления.
Ход луча через
призму рассчитывается на основании
законов преломления света. При преломлении
на первой грани призмы
АС получим
![]()
(12)
где n
– показатель преломления материала
призмы для данной длины волны света.
Для грани АВ
закон преломления запишется как
 .
.
(13)
Соотношения 12 и 13
позволяют найти выражения для определения
n.
Однако экспериментально определить
углы r1
и i1
достаточно
сложно. На практике удобнее измерить
угол отклонения луча призмой δ
и преломляющий
угол призмы φ.
Получим формулу
для определения показателя преломления
n
через углы
δ и φ.
Сначала воспользуемся
известной в геометрии теоремой, что
внешний угол треугольника равен сумме
внутренних углов, не смежных с ним.
Тогда из треугольника EDF
получим
φ= r1+i2
.
(14)
Из треугольника
EHF
и, используя (14), получим:
δ=(i1
–
r1)+(r2
–
i2)=
i1+r2
–(r1+
i2)=
i1+r2+
φ.
(15)
Затем выразим угол
δ
через угол r1
, используя законы преломления (12), (13) и
(14), и определим условия минимальности
δ:
i1
= arcsin(n sin r1);
r2
=
arcsin(n
sin i2)
= arcsin(n sin (φ-
r1));
δ
=
arcsin(n
sin r1)
+arcsin(n sin (φ-
r1)).
Зависимость δ
от r1
имеет минимум, условие которого можно
найти, приравняв производную δ
от r1
нулю:
![]() (16)
(16)
Выражение (16)
выполняется, если r1=
φ
– r1.
В соответствии
с (14) имеем φ
– r1=
i2,
поэтому
r1
= i2.
Тогда из
законов преломления (12) и (13) следует,
что углы i1,
r2
также должны
быть равны:
i1=r2.
Принимая во внимание (14) и (15), получим:
φ
= 2r1;
δmin=2i1
– φ.
C
учетом
этих равенств окончательно получим:
![]() и
и
![]() .
.
Следовательно, при
наименьшем
угле отклонения луча призмой δmin
показатель преломления вещества призмы
может быть определен по формуле
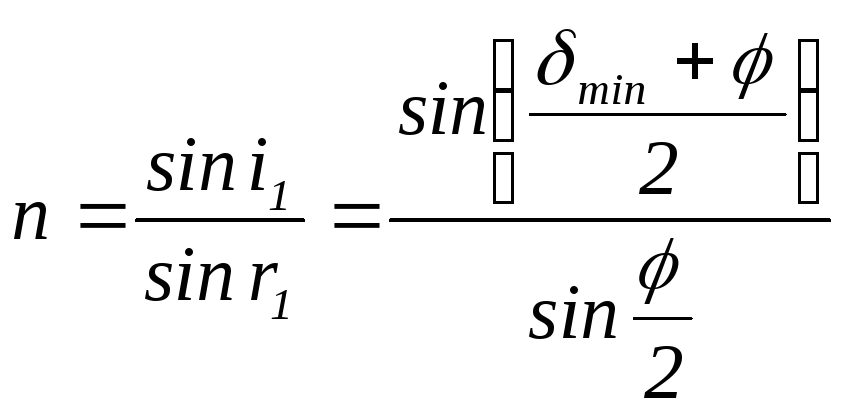 .
.
(17)
Таким образом,
определение показателя преломления
вещества сводится к измерению преломляющего
угла призмы
и угла
наименьшего отклонения
лучей.
Угол наименьшего
отклонения δ
образован
двумя направлениями: направлением луча,
падающего на призму S1
и направлением луча, вышедшего из призмы
S2.
Если источник излучения не является
монохроматическим, то из-за дисперсии
вещества призмы направление преломленного
луча ЕF,
а, следовательно, и направление вышедшего
луча S2
будут
различными для разных длин волн, т.е.
S2=f(λ).
Это приводит к тому, что δ
и n для
разных λ,
будут
различными.
Преломляющий угол
призмы φ
образован гранью призмы СА,
на которую падает луч и гранью АВ,
из которой выходит излучение, или
перпендикулярами к этим граням А1
и А2
соответственно.
Источником излучения
в работе служит ртутная лампа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
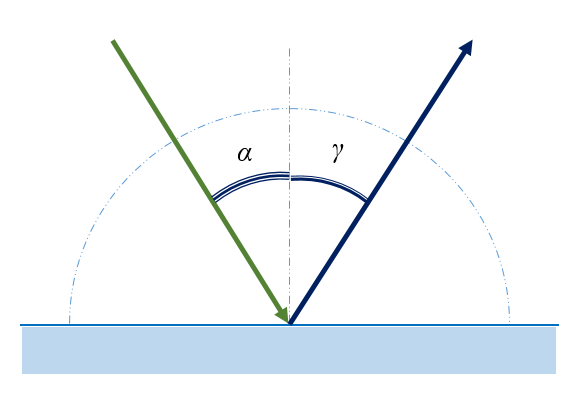
Вывод на основе принципа Гюйгенса:
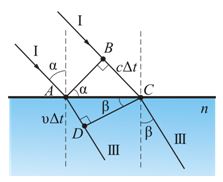
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
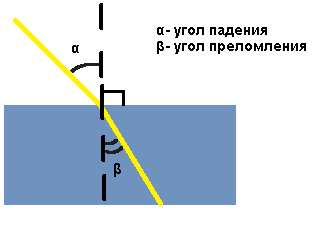
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
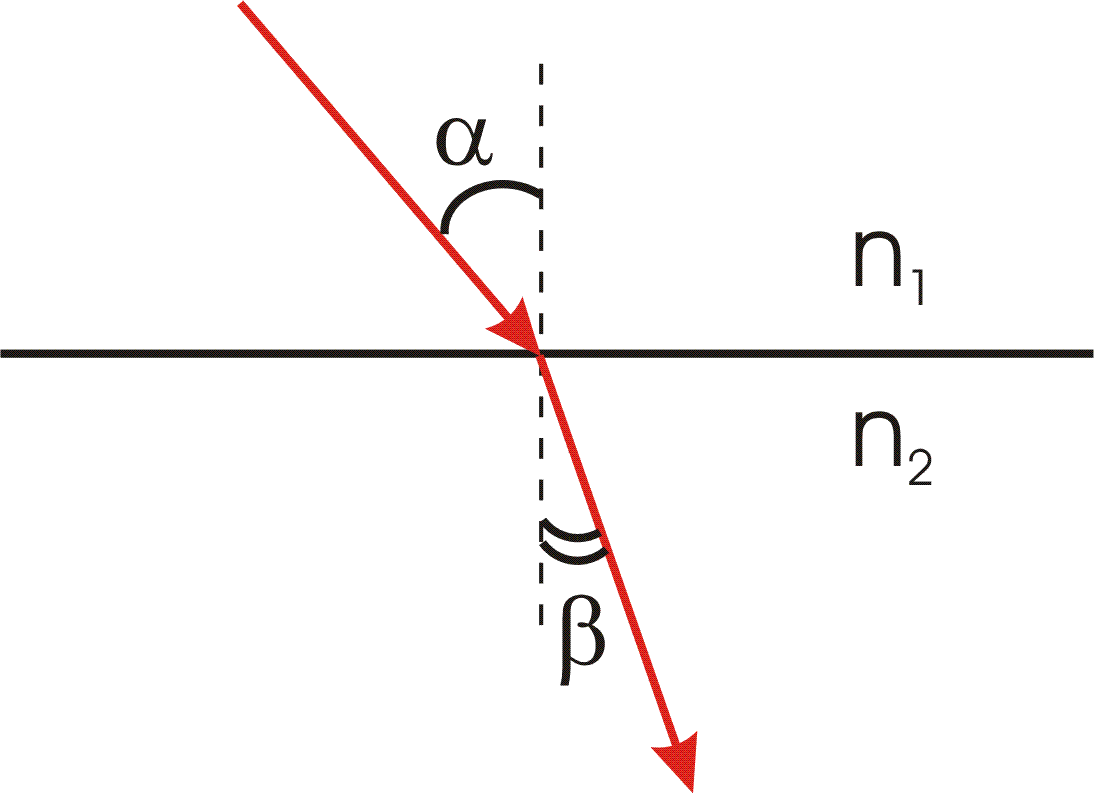

Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что
 , т.е.
, т.е.  .
.
Отсюда следует закон Снелиуса:
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
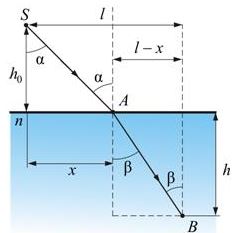
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:
 .
.
Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:
 ,
,
отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса:  .
.
Следствия из принципа Ферма:
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
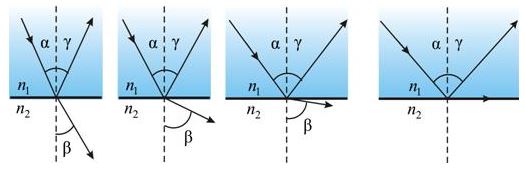
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
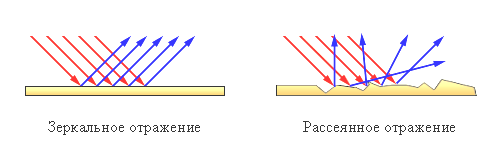
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда – воздух

Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
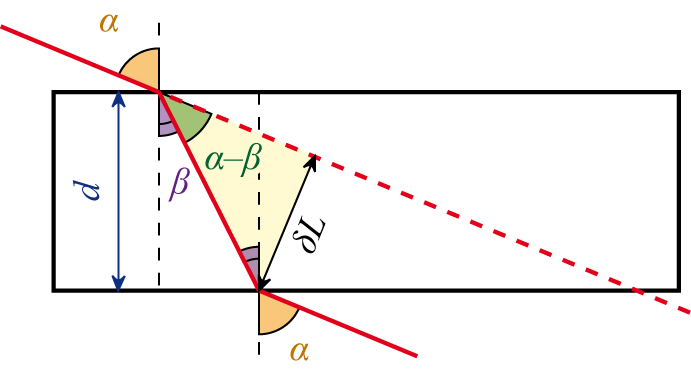
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
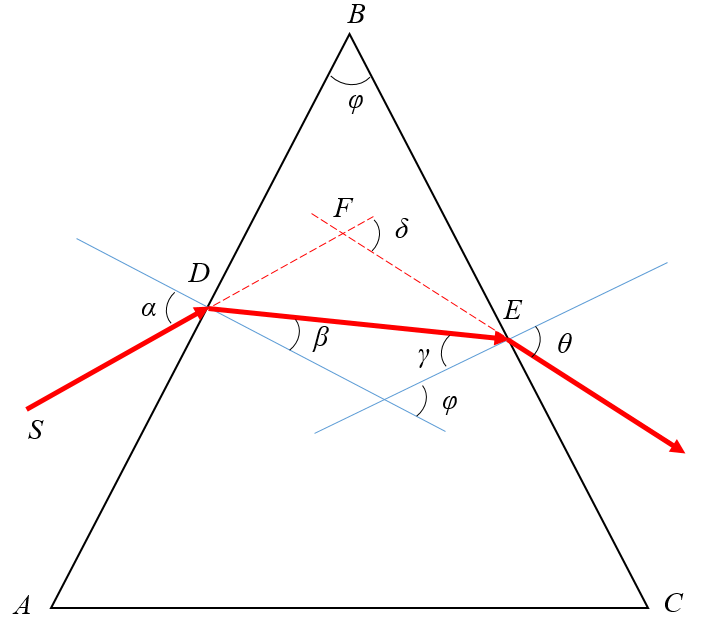
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
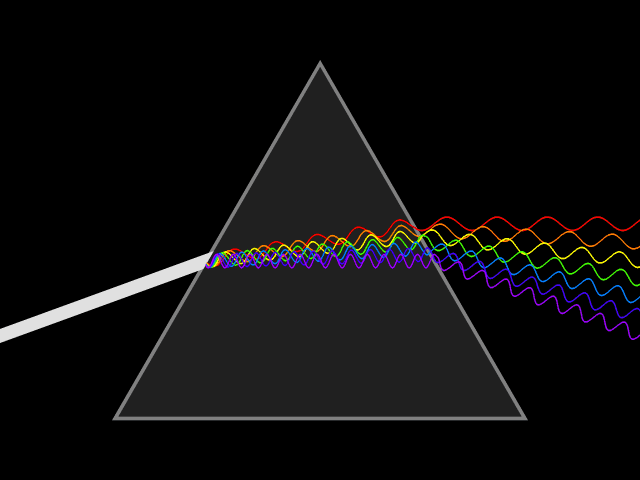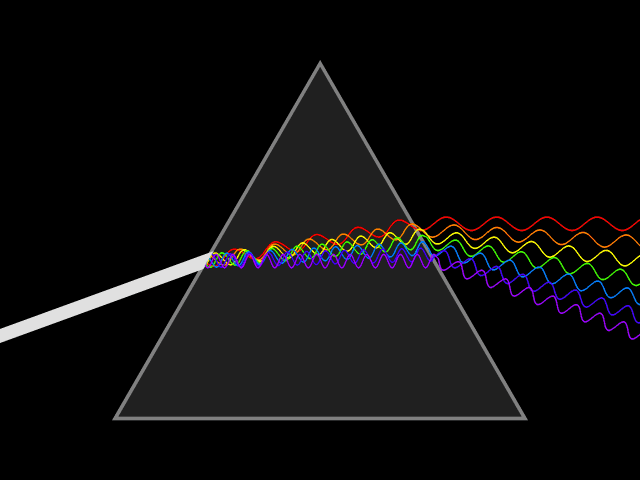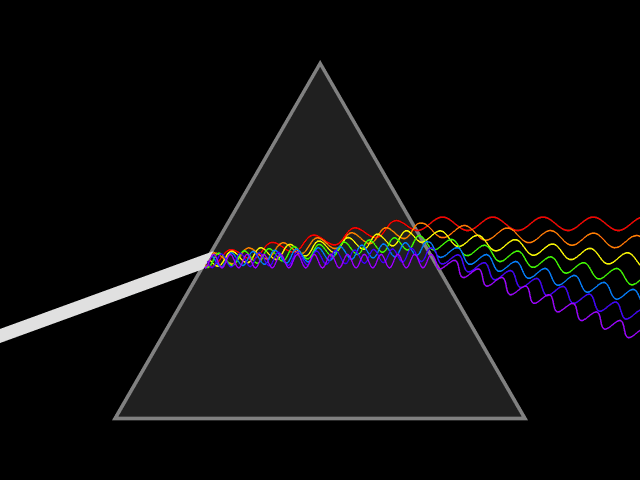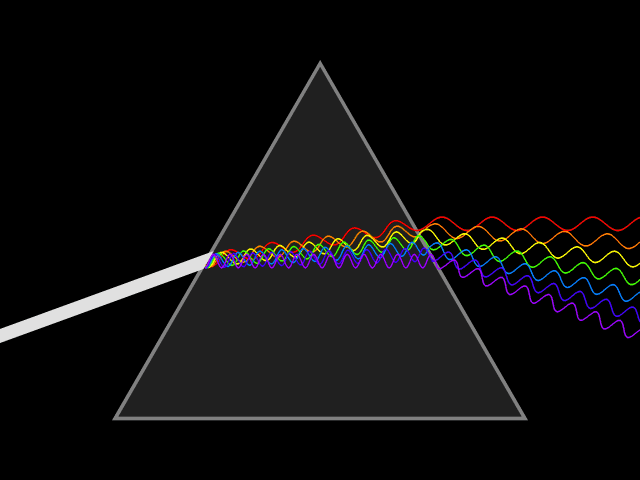
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.


Геометрическая оптика: призмы
В этой статье решаем задачи с призмами. Будем применять закон преломления Снеллиуса, а также геометрические знания.
Задача 1.
Монохроматический луч падает нормально на боковую поверхность призмы, преломляющий угол которой равен . Показатель преломления материала призмы для этого луча равен 1,5. Найдите угол отклонения луча, выходящего из призмы, от первоначального направления.
Так как луч падает нормально на поверхность призмы, то не преломляется на этой поверхности. На вторую же боковую грань он упадет под некоторым углом, и преломится на ней.

К задаче 1
В треугольнике (прямоугольном) угол
по условию, поэтому второй острый угол равен
. Поэтому угол падения луча на вторую грань равен
. Зная показатель преломления, можно найти угол преломления. Нужный нам угол – разность угла преломления и угла падения луча.
По закону преломления
Ответ: .
Задача 2. Луч света входит в стеклянную призму под углом и выходит из призмы в воздух под углом
, причем, пройдя призму, отклоняется от первоначального направления на угол
. Найдите преломляющий угол призмы.

К задаче 2
Рассмотрим рисунок. Угол , смежный с данным углом отклонения луча, равен
. В четырехугольнике
угол
равен
, как вертикальный с углом падения, а угол
равен
как вертикальный с углом преломления. Так как сумма углов четырехугольника равна
, то угол
равен:
Теперь рассмотрим четырехугольник . В нем два угла прямых, поэтому преломляющий угол призмы равен:
Ответ: .
Задача 3.
Световой луч падает по нормали на боковую грань прямой стеклянной призмы, поперечное сечение которой – равнобедренный треугольник, . Показатель преломления материала призмы для этого луча равен 1,5. Определите угол между падающим и вышедшим из призмы лучами.
Рассмотрим два случая падения луча.

К задаче 3
В первом случае ход луча показан рыжим цветом. На боковой грани призмы луч не преломится, так как падает на нее нормально. Найдем угол падения луча на нижнюю поверхность призмы. Угол призмы равен
– так как треугольник равнобедренный. Тогда в треугольнике
угол
. А угол падения луча
равен
. Для данного показателя преломления предельный угол полного отражения равен
То есть луч не преломится, а отразится от нижней грани призмы. Угол отражения также равен , и, следовательно, угол
. Следовательно, треугольник
подобен
и тоже является прямоугольным. Следовательно, на второй боковой грани призмы луч тоже не преломится, и выйдет под углом
по отношению к падающему (угол
, искомый – смежный с ним).
Ответ: .
Теперь рассмотрим второй случай падения луча.

К задаче 3
Снова на первой боковой грани не произойдет преломления. На вторую боковую грань луч упадет под углом , что тоже превышает предельный угол полного отражения, и далее луч попадет на нижнюю грань призмы, падая на нее под углом
. В треугольнике
угол
, угол
. Определим угол
:
Определим угол :
Определим угол отклонения луча: в треугольнике угол
, угол
, следовательно, искомый угол
Ответ: .
Задача 4.
Тонкий световой луч падает на боковую грань стеклянной призмы из воздуха под углом . Угол между боковыми гранями призмы равен
. Показатель преломления воздуха равен 1, а стекла 1,41. Определите угол смещения луча от первоначального направления
.

К задаче 4
Определим угол преломления .
Рассмотрим четырехугольник . В нем два угла – прямые, преломляющий угол призмы –
, тогда угол
(это следует из суммы углов четырехугольника). Следовательно, из суммы углов треугольника можем определить угол
в одноименном треугольнике:
Найденный нами угол – не что иное, как угол падения луча на вторую грань призмы. Тогда данный луч выйдет из призмы, не преломившись, так как падает перпендикулярно границе раздела.
Тогда искомый угол – угол – равен разности угла
и угла преломления
, то есть
.
Ответ: .