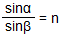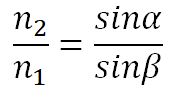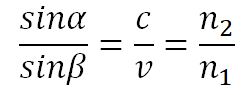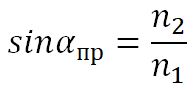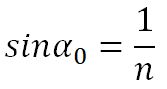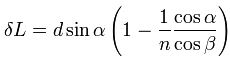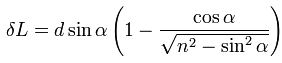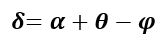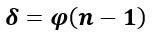Как найти угол отклонения луча света - Сайт, где вы сможете решить свои вопросы

Условие задачи:

Определить угол отклонения лучей монохроматического света с длиной волны 0,55 мкм в спектре первого порядка, полученном с помощью дифракционной решетки, период которой 0,02 мм.

Задача №10.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(lambda=0,55) мкм, (k=1), (d=0,02) мм, (varphi-?)

Решение задачи:

Запишем формулу дифракционной решетки:

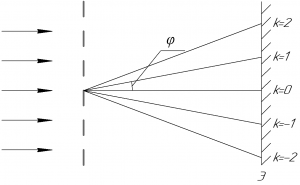
[dsin varphi = klambda;;;;(1)]

В этой формуле (d) – период решетки (также называют постоянной решетки), (varphi) – угол дифракции, (k) – порядок максимума (по условию задачи – первый максимум), (lambda) – длина волны, падающей нормально на решетку.

Из формулы (1) выразим искомый угол дифракции для максимума первого порядка ((k=1) по условию):

[sin varphi = frac{{klambda }}{d}]

[varphi = arcsin left( {frac{{klambda }}{d}} right)]

Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:

[varphi = arcsin left( {frac{{1 cdot 0,55 cdot {{10}^{ – 6}}}}{{0,02 cdot {{10}^{ – 3}}}}} right) = 1,58^circ ]

Ответ: 1,58°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.6.6 Тонкая мыльная пленка освещается светом с длиной волны 0,6 мкм. Чему равна
10.7.2 Один миллиметр дифракционной решетки содержит 20 штрихов. На какой угол отклоняются
10.7.3 Дифракционная решетка имеет 250 штрихов на миллиметр. Под каким углом виден максимум

Источник

17:22

Найти угол отклонения нормально падающего луча призмой

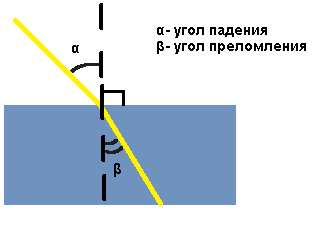
Задача. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определить угол отклонения φ луча призмой, если ее преломляющий угол А = 30°.

Решение задачи по физике:

Для решения данной задачи по геометрической оптике воспользуемся законом преломления света:

Закон преломления света

Преломление света — явление, при котором луч света, переходя из одной среды в другую, изменяет направление на границе этих сред.

Преломление света происходит по следующему закону:
Падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред:
,
где α — угол падения,
β — угол преломления,
n — постоянная величина, не зависящая от угла падения.

При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Если свет идет из среды оптически менее плотной в более плотную среду, то угол преломления всегда меньше угла падения: β < α.
Луч света, направленный перпендикулярно к границе раздела двух сред, проходит из одной среды в другую без преломления.

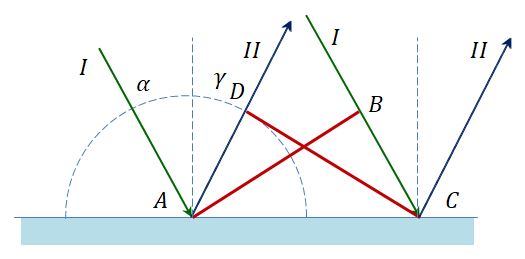
Рисунок для решения нашей задачи по физике имеет вид

Из закона преломления света следует, что

$$frac{sinalpha }{sinbeta }=n$$

Отсюда получаем, что

$$sinalpha =nsinbeta Rightarrow alpha =arcsinleft ( nsinbeta right )$$

Из геометрии рисунка видно, что

$$beta =A,varphi =alpha -beta =alpha -A$$

Подставляем значения и находим:

$$alpha =arcsinleft ( nsinbeta right ) =arcsinleft ( 1.5sin30 right )=48.59^{circ}$$

Угол отклонения луча призмой будет равен:

$$varphi =alpha -A=48.59-30=18.59^{circ}=18^{circ}36{}’$$
Решение контрольных работ

Категория: Решение задач по физике | Просмотров: 15264 | | Теги: геометрическая оптика, нормадьно подает луч, грань стеклянной призмы, закон преломления света | Рейтинг: 3.4/7

Источник

Принцип Гюйгенса:

Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

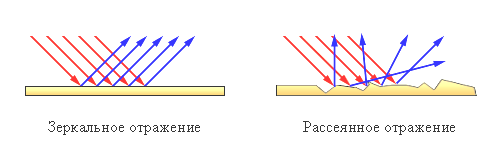
Закон отражения:

отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
угол падения α равен углу отражения γ:

α = γ

otr

Вывод на основе принципа Гюйгенса:

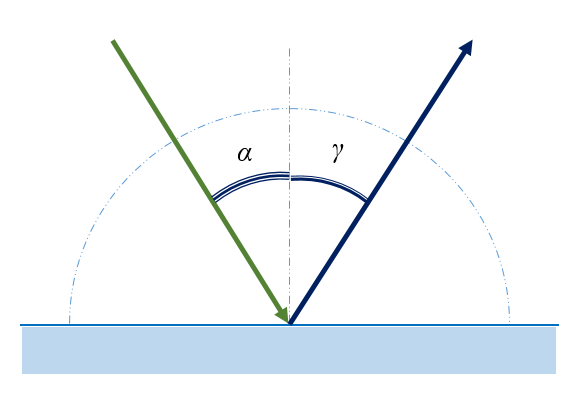
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.

Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.

Закон преломления (закон Снелиуса):

луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.

pl par Prel

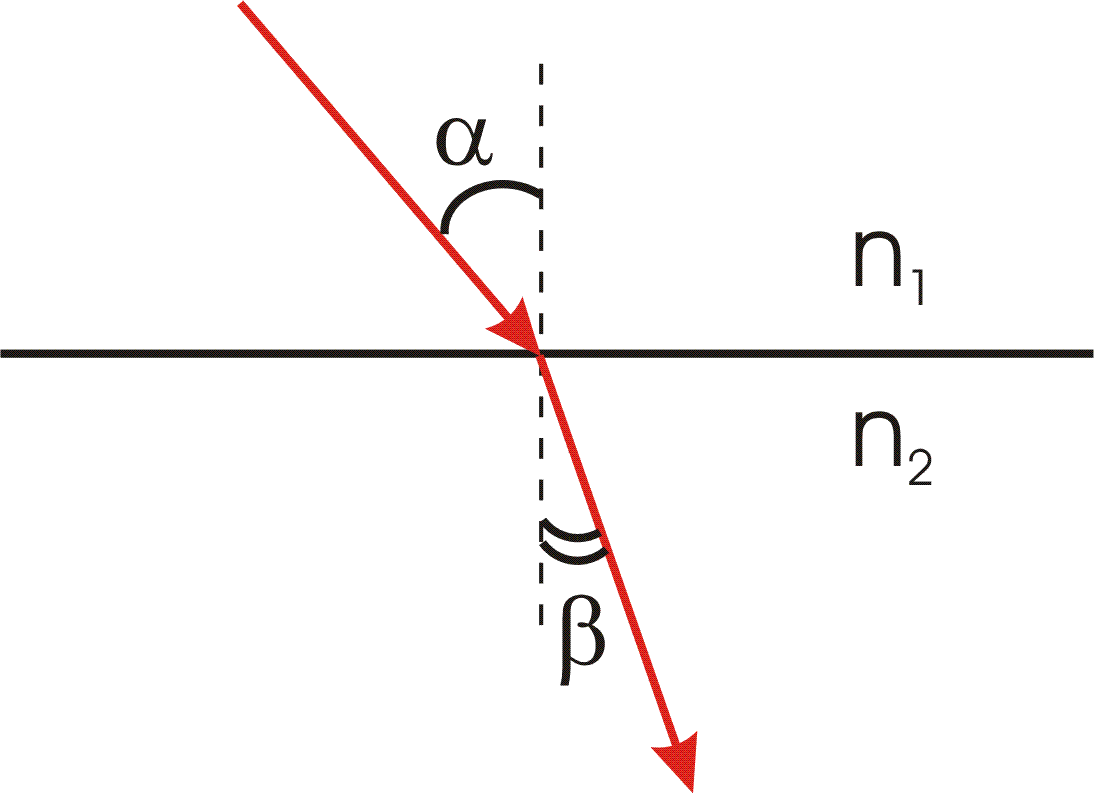
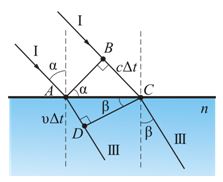
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.

Prel1

Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что

, т.е. .

Отсюда следует закон Снелиуса:

Prel2

Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.

Покажем применение этого принципа к решению той же задачи о преломлении света.

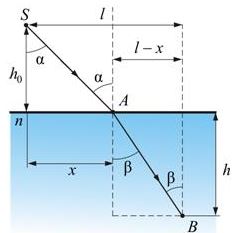
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела

Ferma

В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: .

Следствия из принципа Ферма:

1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.

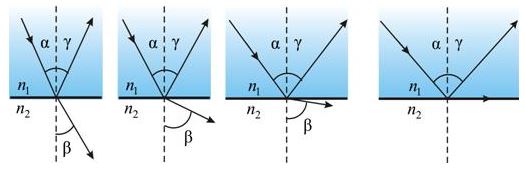
2. Если свет распространяется из среды с большим показателем преломления n₁ (оптически более плотной) в среду с меньшим показателем преломления n₂ (оптически менее плотной) ( n₁ > n₂ ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:

Prel3

3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = α_пр) угол преломления не окажется равным π/2.

Полное отражение

Угол α_пр называется предельным углом полного отражения. При углах падения α > α_пр весь падающий свет полностью отражается.

По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.

Если α = α_пр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.

Таким образом, при углах падения в пределах от α_пр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.

В случае, если вторая среда – воздух

Преломление света в плоскопараллельной пластине

Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.

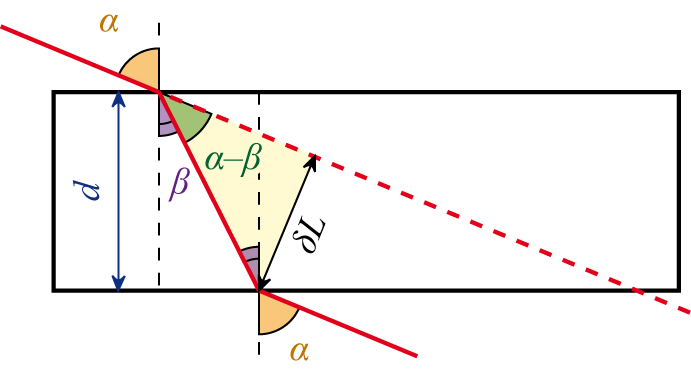
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча

Величина смещения в плоскопараллельной пластине

Величина сдвига луча света δL зависит:

от угла падения света α,
от толщины пластины d,
от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.

C увеличением любого из этих параметров смещение луча света увеличивается.

Smesch

Смещение луча можно выразить через угол падения

Smesch1

Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:

угол падения равен нулю: α = 0,
относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
толщина пластины равна нулю: d = 0

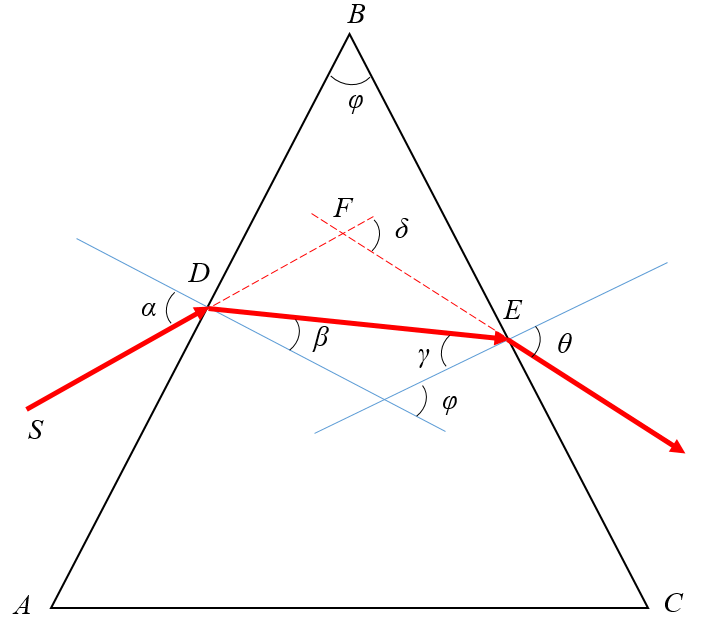
Ход луча через треугольную призму

Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.

prisma1

На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.

Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой

Delta

Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой

Delta1

Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.

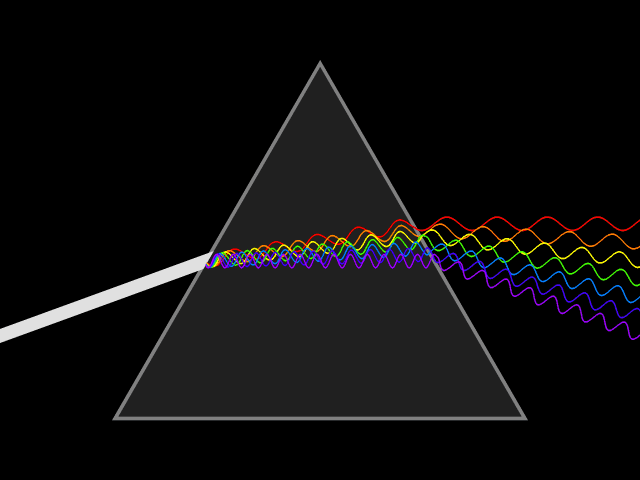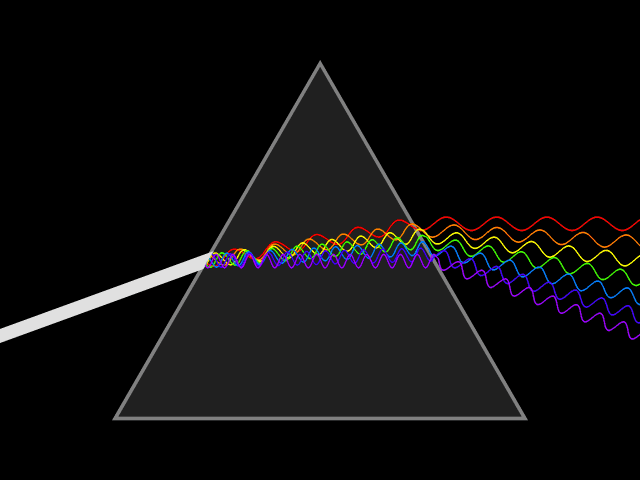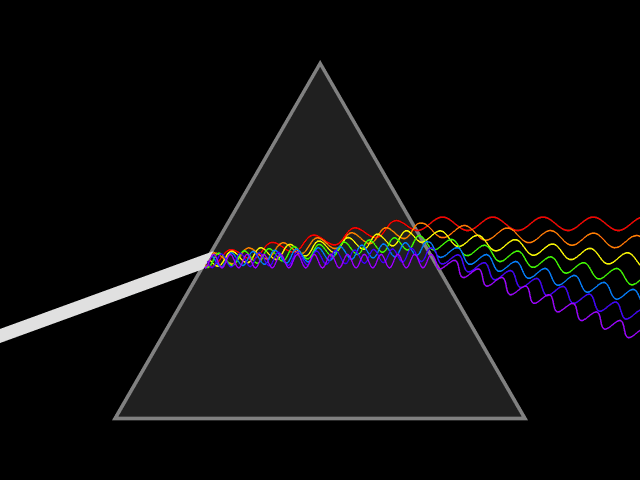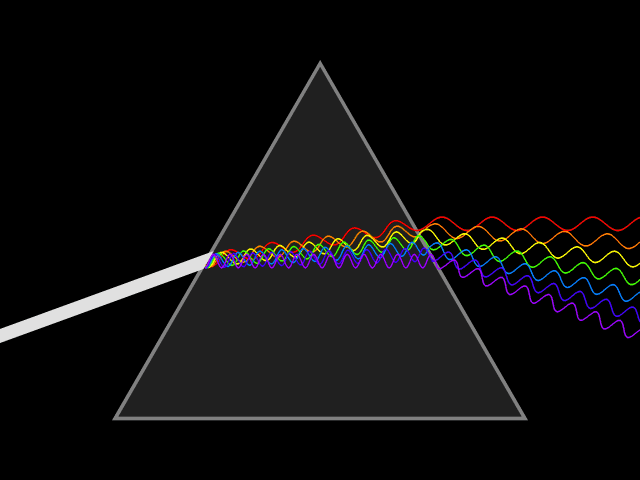
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.

Источник

2.2. Рассмотрим движение фермионов и фотонов в полях тяготения

2.2.1. Рассеяние фермиона (частицы) полем Земли

На какой угол изменится направление скорости частицы под действием поля земного тяготения (рис.1)? Скорость частицы на бесконечности равна $v_{oo}$ . Учитываем, что частица движется по гиперболической траектории. Геометрические свойства гиперболы позволяют доказать, что угол рассеяния , прицельное расстояние и расстояние $r_{m}$ от центра планеты до ближайшей точки траектории частицы связаны соотношением

$tgfrac{Theta }{2}=frac{b^2-r_{m}^2}{2br_{m}}$

Действительно, гипербола – это геометрическое место точек, разность расстояний до которых от двух заданных точек и , называемых фокусами (рис.2), постоянна: $r_{1}-r_{2}=const$ . Один из фокусов гиперболы совпадает с центром Земли, второй фокус лежит на прямой, проходящей через центр Земли и и ближайшую к центру точку траектории.

На бесконечно больших расстояниях от Земли как при приближении, так и при удалении скорость частицы направлена по асимптоте гиперболы, поэтому задача состоит в нахождении угла между асимптотами. Точка пересечения асимптот лежит посередине между фокусами.

Приравняем разности расстояний от фокусов и до бесконечно удаленной точки – это отрезок на рисунке 2 – и до ближайшей к центру Земли точки. Из треугольника находим ,

$O'C=2btgfrac{Theta }{2}$ , $OO'=frac{2b}{cosfrac{Theta }{2}}$ .

Разность расстояний от фокусов до точки составляет

где $BO=r_{m}$ .

Теперь условие равенства разности расстояний до выбранных точек можно записать в виде

$2btgfrac{Theta }{2}=frac{2b}{cosfrac{Theta }{2}}-2r_{m}$ .

Перенося $2r_{m}$ в левую часть, возводя обе части в квадрат и используя тождество

$frac{1}{cos^2Theta }=1+tg^2Theta$

получаем формулу .

Запишем теперь законы сохранения энергии и момента импульса частицы для участка её траектории (см. рис.1):

$E_{A}=E_{B}$ , $L_{A}=L_{B}$ или

$frac{mv_{oo}^2}{2}=frac{mv_{m}^2}{2}-frac{GMm}{r_{m}}$ ,

$bv_{oo}=r_{m}v_{m}$ ,

где $v_{m}$ – скорость частицы в точке ; мы учли, что точка находится в бесконечности, поэтому $L_{A}=L_{oo}=r_{0}mv_{oo}sinalpha _{0}=bmv_{oo}$ , а

$L_{B}=r_{m}mv_{m}sin90°=r_{m}mv_{m}$ . (Вместо закона сохранения момента импульса можно использовать второй закон Кеплера). Из равенства получаем

$r_{m}^2+frac{2GM}{v_{oo}^2}r_{m}-b^2=0$ .

Если считать заданным расстояние $r_{m}$ , то для прицельного расстояния находим

$b=r_{m}sqrt{1+frac{2GM}{r_{m}v_{oo}^2}}$ .

Если считать заданным расстояние , то для $r_{m}$ находим

$r_{m}=frac{2GM}{v_{oo}^2}left(sqrt{1+left(frac{bv_{oo}^2}{GM} right)^2} -1right)$ .

Для определенности будем считать известным прицельный параметр . Тогда, с учетом (3), для угла рассеяния получаем

$tgfrac{Theta }{2}=frac{GM}{bv_{oo}}$

Частица не задевает планету, если $r_{m}geq R$ (см. рис.1). При $r_{m}=R$ расстояние оказывается минимальным и равным

где $v_{2c}=sqrt{frac{2GM}{R}}$ – вторая космическая (параболическая) скорость. При заданном значении $v_{oo}$ и минимальном прицельном расстоянии $b_{min}$ угол отклонения (рассеяния) максимален: $Theta =Theta _{max}$ и

$tgfrac{Theta _{max}}{2}=frac{left(frac{v_{2c}}{v_{oo}} right)^2}{2sqrt{1+left(frac{v_{2c}}{v_{oo}} right)^2}}=frac{frac{GM}{Rv_{oo}^2}}{sqrt{1+frac{2GM}{Rv_{oo}^2}}}$ .

Отсюда следуют частные случаи:

1) Если $v_{oo}gg v_{2c}$ , то $b_{min}=R$ и, следовательно,

$tgfrac{Theta _{max}}{2}=frac{1}{2}left(frac{v_{2c}}{v_{oo}} right)^2=frac{GM}{Rv_{oo}^2}$ .

Так как $frac{v_{2c}}{v_{oo}}ll 1$ , то $Theta _{max}=frac{2GM}{Rv_{oo}^2}$

(мы учли, что при ).

2) Если $v_{oo}ll v_{2c}$ , то формула для угла рассеяния приводится к виду

$tgfrac{Theta _{max}}{2}=frac{v_{2c}}{2v_{oo}}$ .

В предельном случае, когда $frac{v_{2c}}{v_{oo}}rightarrow$ к бесконечности, получаем $tgfrac{Theta _{max}}{2}rightarrow$ к бесконечности и, следовательно, $Theta _{max}rightarrow 180$ градусов.

Таким образом, при достаточно малых значениях $v_{oo}$ направление скорости частицы при облете центрального тела изменится практически на противоположное.

Задачу можно решить из уравнения траектории частицы в полярных координатах:

$frac{p}{r}=1+epsilon cos varphi$ ,

где – полярный угол, $p=frac{L^2}{2malpha }$ -фокальный параметр частицы, $epsilon =sqrt{1+frac{2EL^2}{alpha ^2m}}$ – эксцентриситет орбиты, , причем , и – полная механическая энергия и момент импульса частицы соответственно. Из начальных условий получаем

Следовательно, эксцентриситет орбиты равен

$epsilon =sqrt{1+left(frac{bv_{oo}^2}{GM} right)^2}$

Так как , частица движется по гиперболической траектории. Из выражения следует, что при расстояние минимально и равно

$r_{m}=frac{p}{1+epsilon }=aleft(epsilon -1 right)$ ,

где $a=frac{p}{epsilon ^2-1}=frac{alpha }{2E}$ – полуось гиперболы. Эту формулу можно привести к виду .

Определим угол $varphi _{m}$ между линией, соединяющей точки и (полярной осью), и направлением асимптоты $K_{1}N_{1}$ , к которой приближается траектория частицы, удаляющейся в бесконечность (см. рис.1).

Поскольку при $varphi =varphi _{m}$ бесконечности, то из формулы получаем

$cosvarphi _{m}=-frac{1}{epsilon }$ .

Угол отклонения и угол $varphi _{m}$ связаны соотношением $Theta =-pi +2varphi _{m}$ , поэтому последнее равенство приобретает вид

$tgfrac{Theta }{2}=frac{1}{sqrt{epsilon ^2-1}}$ .

Эту формулу можно получить непосредственно из свойств гиперболы. Подставляя сюда выражение для , снова получаем формулу .

Задача 2 – Отклонение светового луча Солнцем

Следует оценить угол отклонения луча света при его прохождении вблизи поверхности Солнца.

Масса Солнца $M=2cdot 10^{30}$ кГ, радиус Солнца $R=7cdot 10^{8}$ метров.

Пока для простоты будем считать, что свет состоит из корпускул массой . Так как корпускула имеет массу, её траектория должна искривляться под действием гравитации, подобно тому, как искривляется траектория обычных частиц или тел в полях тяготения центральных тел.

Предположим, что световая корпускула движется в поле звезды по гиперболической траектории (см. рис.1). Если рассматривать световую корпускулу как классическую частицу с кинетической энергией $E_{k}=frac{mv^2}{2}=frac{mC^2}{2}$ , то для оценки угла можем воспользоваться результатами задачи 1: формула теперь принимает вид

$tgfrac{Theta }{2}=frac{GM}{bC^2}$ ,

где . Легко убедиться в том, что для обычных небесных тел массой и радиусом выполняется условие $frac{GM}{RC^2}ll 1$ , ∞,

которое называется условием, или приближением, слабого поля (именно при этом условии поля тяготения являются ньютоновскими). Например, на поверхности Солнца $frac{GM}{RC^2}=10^{-6}$ . Учитывая малость угла , можно записать

$Theta =frac{2GM}{bC^2}$ ,

тогда для светового луча, проходящего вблизи поверхности звезды , получим

$Theta =frac{2GM}{RC^2}$ . Для Солнца .

Заметим, что минимальное расстояние $r_{m}$ по-прежнему определяется формулой , которая при $v_{oo}=C$ принимает вид

$r_{m}=frac{GM}{C^2}left(sqrt{1+left(frac{bC^2}{GM} right)^2} -1right)=bleft(1-frac{GM}{bC^2} right)$ .

Очевидно, что рассмотренный способ решения задачи является некорректным с точки зрения современной физической теории. В рамках данного способа скорость световой корпускулы изменяется от $v_{oo}=C$ до $v_{m}=frac{bv_{oo}}{r_{m}}=frac{bC}{r_{m}}$ .

Понятно, что при $bapprox r_{m}approx R$ $v_{m}approx v_{oo}approx C$ , но это приближение ничего не определяет по существу: скорость света остается переменной величиной. Кроме того, теперь мы знаем, что классическая формула $E_{k}=frac{mv^2}{2}$ , где , к световым частицам неприменима: энергия световой частицы, т.е. кванта света, фотона, определяется формулой Планка-Эйнштейна

а скорость фотона в вакууме всегда равна .

Теперь решим задачу другим способом, исходя из квантовой теории света, движущегося в слабом поле тяготения звезды. Полная энергия фотона равна

$E=hnu - frac{GMm}{r}=hnu left(1-frac{GM}{rC^2} right)=const$

(мы учли, что масса фотона равна $m=frac{hnu }{C^2}$ ). Момент импульса фотона равен

$L=rmCcdot sinalpha =rfrac{hnu }{C}sinalpha =const$ .

Рассмотрим движение фотона на участке траектории, которую по-прежнему будем считать гиперболической (см. рис.1). Законы сохранения энергии: $E_{A}=E_{B}$ и момента импульса $L_{A}=L_{B}$ дают уравнения

$nu_{0}=nu left(1-frac{GM}{r_{m}C^2} right)$ ,

$bnu_{0}=r_{m}nu$ ,

где $nu_{0}$ – частота фотона в точке , находящейся в бесконечности, – частота фотона в точке на расстоянии $r_{m}$ от центра звезды. Из первого уравнения непосредственно следует, что $nu >nu _{0}$ – фиолетовое гравитационное смещение. Из обоих уравнений получаем

$r_{m}^2-br_{m}+frac{GMb}{C^2}=0$ .

Если считать заданным прицельный параметр , то

$r_{m}=frac{b}{2}left(1pm sqrt{1-frac{2R_{g}}{b}} right)$ ,

где $R_{g}=frac{2GM}{C^2}$ – гравитационный радиус (или радиус Шварцшильда). Для обычных небесных тел

$frac{R_{g}}{R}=frac{2GM}{RC^2}ll 1$ , т.е. поля тяготения являются слабыми. Например, гравитационный радиус Солнца равен 3 км.

Так как , то в приближении слабого поля можно записать

$r_{m}=frac{b}{2}left(1pm left(1-frac{R_{g}}{2b} right) right)$ ,

или

$r_{m_{1}}=bleft(1-frac{R_{g}}{2b} right) и (r_{m_{2}}=frac{R_{g}}{2}$ .

Очевидно, что второе решение не имеет смысла, поэтому окончательно получаем

$r_{m}=bleft(1-frac{R_{g}}{2b} right)$ .

Аналогично, для угла отклонения находим

$tgfrac{Theta }{2}=frac{R_{g}}{2b}=frac{GM}{bC^2}$ ,

$Theta =frac{R_{g}}{b}=frac{2GM}{bC^2}$ .

Как видим, в приближении слабого поля результаты, полученные с обеих точек зрения – классической и квантовой – полностью совпадают.

Поправка ОТО

Отметим, что в 1915 году расчет угла отклонения выполнил Альберт Эйнштейн. Согласно ОТО, в поле тяготения изменяются законы геометрии и ход времени. Из уравнений ОТО следует, что траектория светового луча в слабом поле тяготения звезды определяется уравнением

$frac{frac{b^2C^2}{GM}}{r}=1+frac{bC^2}{GM}cosvarphi +sin^2varphi$ .

Как видно, это уравнение отличается от уравнения траектории классической световой корпускулы членом . Учитывая, что $Theta =-pi +2varphi _{m}$ , получаем формулу Эйнштейна для угла отклонения светового луча:

$Theta =frac{2R_{g}}{b}=frac{4GM}{bC^2}$ .

Для луча, проходящего вблизи поверхности звезды , этот угол равен

$Theta =frac{4GM}{RC^2}$ .

Для Солнца .

Следствие из фотонной физики

Частица вещества, для которой и производились расчеты, представляет из себя пару одночастотных и синфазных фотонов. Это система устойчива и, будучи разогнана до скорости света, остается устойчивой. Как видно из анимации, фотоны остаются в составе пары. При этом стоит заметить, что на отклонение в поле гравитации на каждый фотон влияет не только собственное инерционное поле, но и поле второго фотона. Поэтому угол отклонения фотонов в паре будет в два раза меньший. Если один из фотонов убрать, то на отклонение фотона полем гравитации центрального тела будет влиять только собственное инерционное поле. Поэтому для угла отклонения следует использовать формулу $Theta =frac{4GM}{RC^2}$ , что соответствует решению Эйнштейна. При этом, в отличие от фотона, для вещества по-прежнему будет справедлива формула $Theta =frac{2GM}{RC^2}$ .

Разгон вещества

Источник

На какой угол отклонится луч света от первоначального направления, упав под углом 45° на поверхность стекла; на поверхность алмаза?

reshalka.com

ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Преломление света. Дисперсия света. Номер №1990

Решение

Дано:
α = 45°.
Найти:

− ?

− ?
Решение:
Показатель преломления стекла равен 1,6, показатель преломления алмаза − 2,42.
По закону преломления:

n
=

s
i
n

;

=
a
r
c
s
i
n
(

s
i
n

)
;
Найдем угол отклонения луча света:

−

−
a
r
c
s
i
n

s
i
n

=
45

−
a
r
c
s
i
n
(

s
i
n
45

1
,
6

)
=
45

−
a
r
c
s
i
n
0
,
442
=
45

−
26

=
19

;

−

−
a
r
c
s
i
n

s
i
n

=
45

−
a
r
c
s
i
n
(

s
i
n
45

2
,
42

)
=
45

−
a
r
c
s
i
n
0
,
292
=
45

−
17

=
28

.
Ответ: 19°; 28°.

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 1,58°.

Смотрите также задачи:

Закон преломления света

Ход луча через треугольную призму

ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Преломление света. Дисперсия света. Номер №1990

Решение

Вам также может понравиться

Как найти цветы дьявола

Как найти массу криптона

Как найти файл в кэше компьютера

Добавить комментарий Отменить ответ