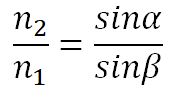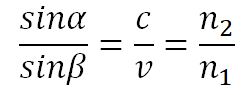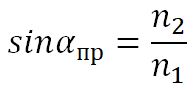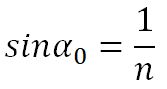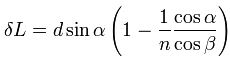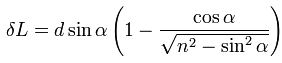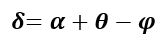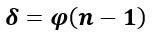Условие задачи:
Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°. Угол падения луча на грань призмы равен 30°, а показатель преломления вещества призмы равен 1,5.
Задача №10.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
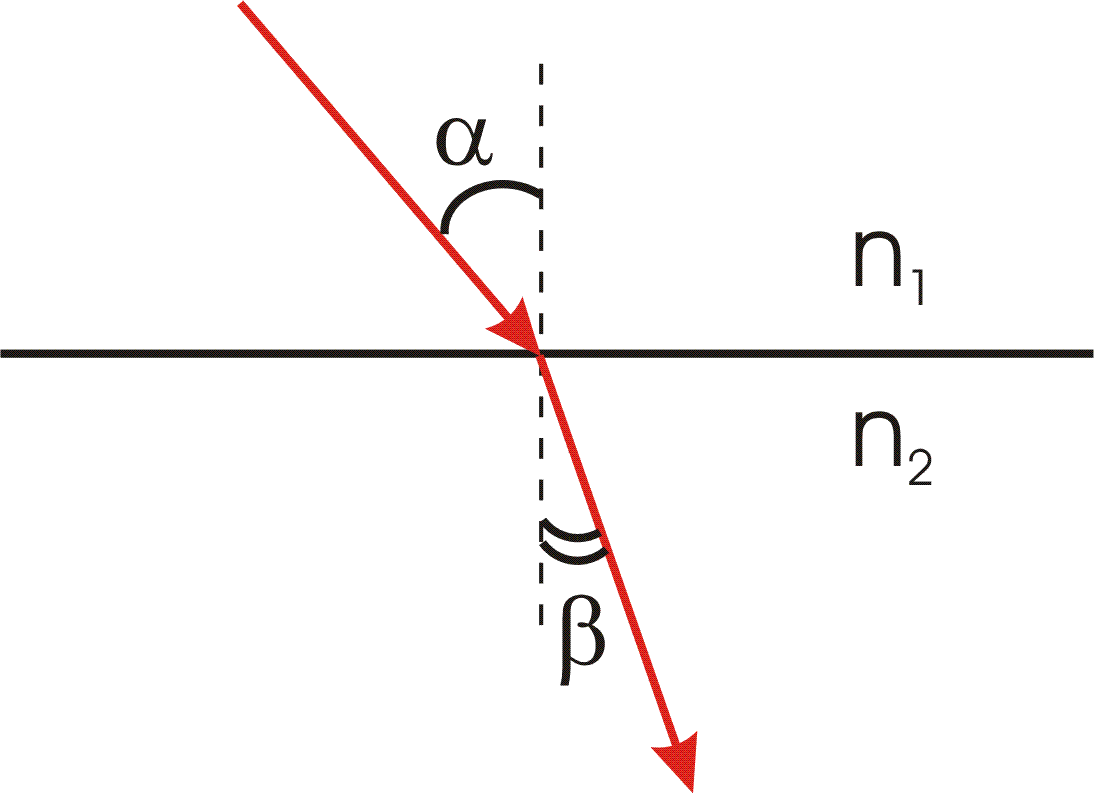
(varphi=60^circ), (alpha=30^circ), (n_1=1,5), (theta-?)
Решение задачи:
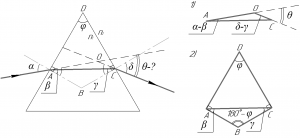 Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Рассмотрим треугольник AOC (смотрите рисунок 1). Искомый угол (theta) является смежным для этого треугольника, поэтому справедливо:
[theta = left( {alpha – beta } right) + left( {delta – gamma } right)]
[theta = alpha + delta – left( {beta + gamma } right);;;;(1)]
Далее рассмотрим четырёхугольник ABCD (смотрите рисунок 2). В этом четырехугольнике два угла – прямые, поэтому угол ABC равен (left( {180^circ – varphi } right)). На этом рисунке теперь рассмотрим треугольник ABC. Сумма углов любого треугольника равна 180°, поэтому будет верно записать:
[beta + gamma + left( {180^circ – varphi } right) = 180^circ ]
[varphi = beta + gamma ;;;;(2)]
Тогда уравнение (1) примет вид:
[theta = alpha + delta – varphi ;;;;(3)]
Чтобы найти угол преломления (delta), запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin gamma = {n_2}sin delta ]
Здесь (gamma) и (delta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_2) равен 1. Тогда:
[sin delta = frac{{{n_1}sin gamma }}{{{n_2}}}]
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin gamma } right)]
Из равенства (2) также следует, что (gamma = varphi – beta), поэтому:
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – beta } right)} right);;;;(4)]
Чтобы найти угол преломления (beta), опять запишем закон преломления света:
[{n_2}sin alpha = {n_1}sin beta ]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Тогда:
[sin beta = frac{{{n_2}sin alpha }}{{{n_1}}}]
[beta = arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)]
Полученное выражение подставим в (4):
[theta = alpha – varphi + arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)} right)} right)]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[theta = 30^circ – 60^circ + arcsin left( {frac{{1,5}}{1}sin left( {60^circ – arcsin left( {frac{{1 cdot sin 30^circ }}{{1,5}}} right)} right)} right) = 47,1^circ ]
Ответ: 47,1°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.37 Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает
10.3.39 Луч света входит в стеклянную призму под углом π/6 и выходит из призмы в воздух
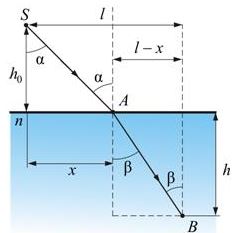
10.3.40 Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды
11
3.1. Определение показателя преломления веществ по углу наименьшего отклонения
Рассмотрим метод
определения показателя преломления,
применимый для прозрачных веществ.
Метод состоит в измерении угла отклонения
лучей при прохождении света через
призму, изготовленную из исследуемого
материала. На призму направляется
параллельный пучок лучей, поэтому
достаточно рассмотреть ход одного из
них (S1)
в плоскости, перпендикулярной линии
пересечения
луча преломляющих
граней призмы (рис.6).
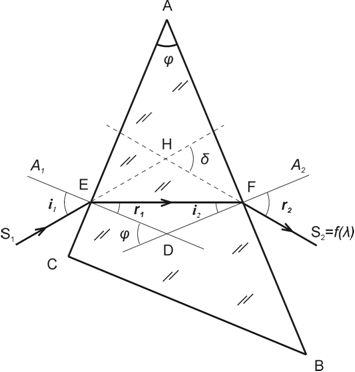
Рис.6.
S1─направление
луча, падающего на призму,
S2─
направление луча, вышедшего из призмы,
А1─направление
нормали к грани, на которую падает луч
S1,
А2─
направление нормали к грани, из которой
выходит луч S2,
i1,
i2
– углы падения,
r1,
r2
– углы преломления на границах раздела
АС и АВ
соответственно,
φ
– преломляющий угол призмы,
δ
– угол отклонения выходящего из призмы
луча относительно первоначального
направления.
Ход луча через
призму рассчитывается на основании
законов преломления света. При преломлении
на первой грани призмы
АС получим
![]()
(12)
где n
– показатель преломления материала
призмы для данной длины волны света.
Для грани АВ
закон преломления запишется как
 .
.
(13)
Соотношения 12 и 13
позволяют найти выражения для определения
n.
Однако экспериментально определить
углы r1
и i1
достаточно
сложно. На практике удобнее измерить
угол отклонения луча призмой δ
и преломляющий
угол призмы φ.
Получим формулу
для определения показателя преломления
n
через углы
δ и φ.
Сначала воспользуемся
известной в геометрии теоремой, что
внешний угол треугольника равен сумме
внутренних углов, не смежных с ним.
Тогда из треугольника EDF
получим
φ= r1+i2
.
(14)
Из треугольника
EHF
и, используя (14), получим:
δ=(i1
–
r1)+(r2
–
i2)=
i1+r2
–(r1+
i2)=
i1+r2+
φ.
(15)
Затем выразим угол
δ
через угол r1
, используя законы преломления (12), (13) и
(14), и определим условия минимальности
δ:
i1
= arcsin(n sin r1);
r2
=
arcsin(n
sin i2)
= arcsin(n sin (φ-
r1));
δ
=
arcsin(n
sin r1)
+arcsin(n sin (φ-
r1)).
Зависимость δ
от r1
имеет минимум, условие которого можно
найти, приравняв производную δ
от r1
нулю:
![]() (16)
(16)
Выражение (16)
выполняется, если r1=
φ
– r1.
В соответствии
с (14) имеем φ
– r1=
i2,
поэтому
r1
= i2.
Тогда из
законов преломления (12) и (13) следует,
что углы i1,
r2
также должны
быть равны:
i1=r2.
Принимая во внимание (14) и (15), получим:
φ
= 2r1;
δmin=2i1
– φ.
C
учетом
этих равенств окончательно получим:
![]() и
и
![]() .
.
Следовательно, при
наименьшем
угле отклонения луча призмой δmin
показатель преломления вещества призмы
может быть определен по формуле
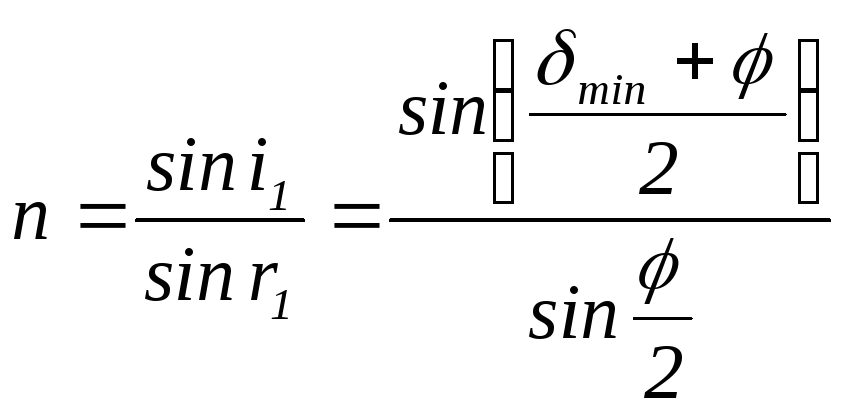 .
.
(17)
Таким образом,
определение показателя преломления
вещества сводится к измерению преломляющего
угла призмы
и угла
наименьшего отклонения
лучей.
Угол наименьшего
отклонения δ
образован
двумя направлениями: направлением луча,
падающего на призму S1
и направлением луча, вышедшего из призмы
S2.
Если источник излучения не является
монохроматическим, то из-за дисперсии
вещества призмы направление преломленного
луча ЕF,
а, следовательно, и направление вышедшего
луча S2
будут
различными для разных длин волн, т.е.
S2=f(λ).
Это приводит к тому, что δ
и n для
разных λ,
будут
различными.
Преломляющий угол
призмы φ
образован гранью призмы СА,
на которую падает луч и гранью АВ,
из которой выходит излучение, или
перпендикулярами к этим граням А1
и А2
соответственно.
Источником излучения
в работе служит ртутная лампа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
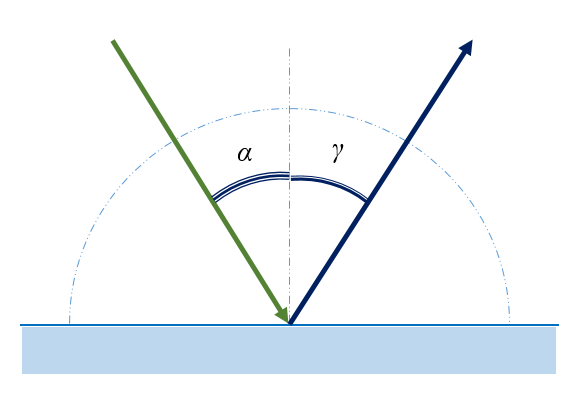
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
Вывод на основе принципа Гюйгенса:
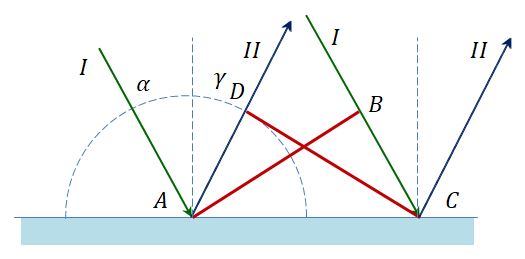
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
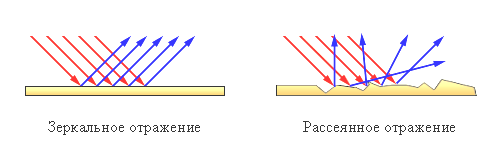
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.

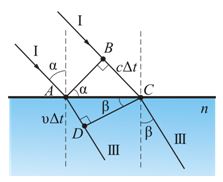
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что
 , т.е.
, т.е.  .
.
Отсюда следует закон Снелиуса:
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:
 .
.
Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:
 ,
,
отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса:  .
.
Следствия из принципа Ферма:
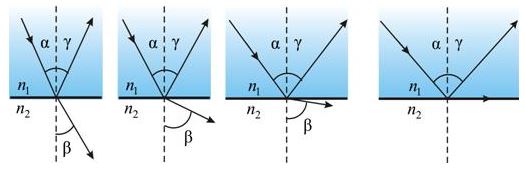
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда – воздух

Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
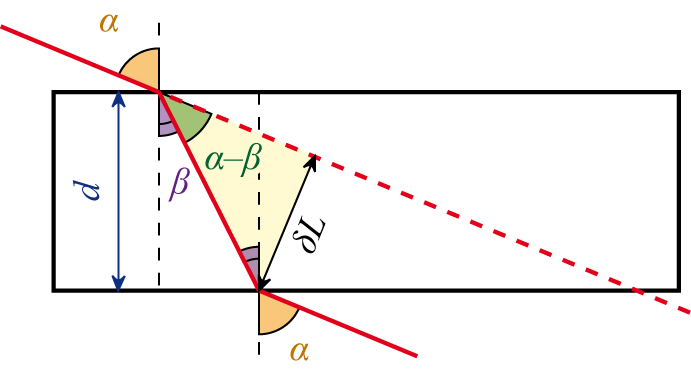
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
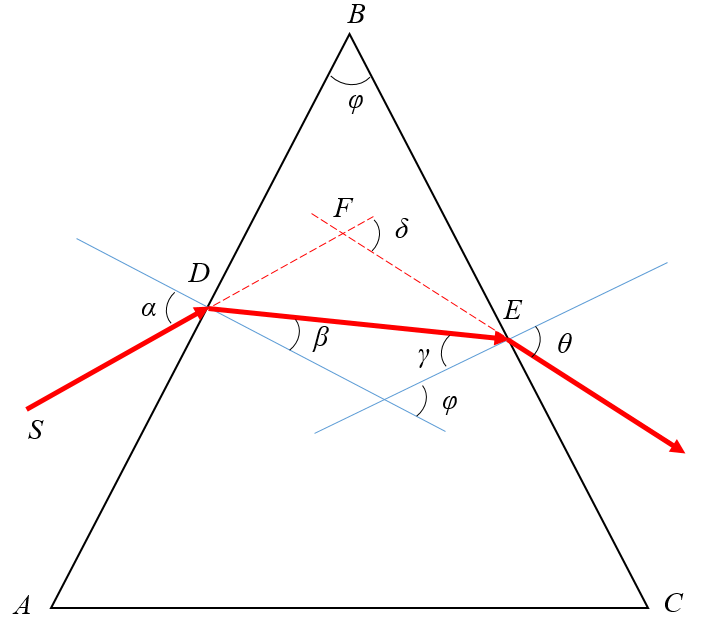
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
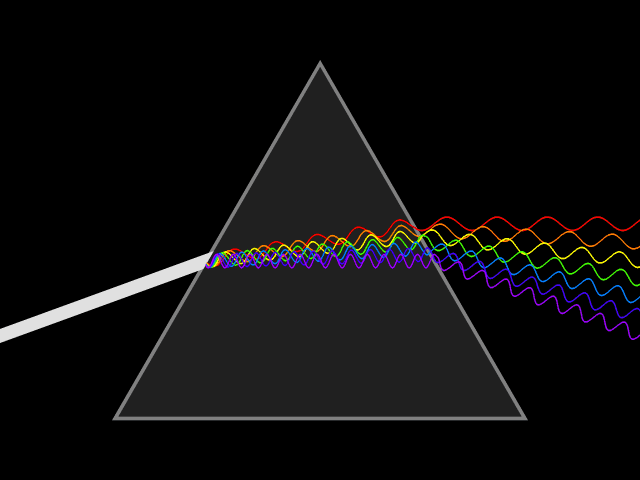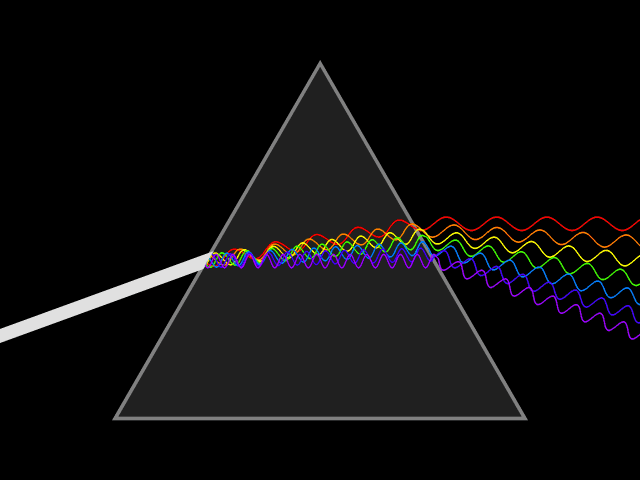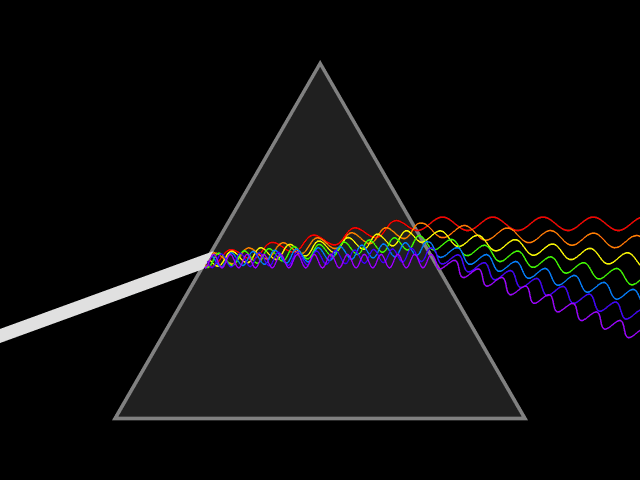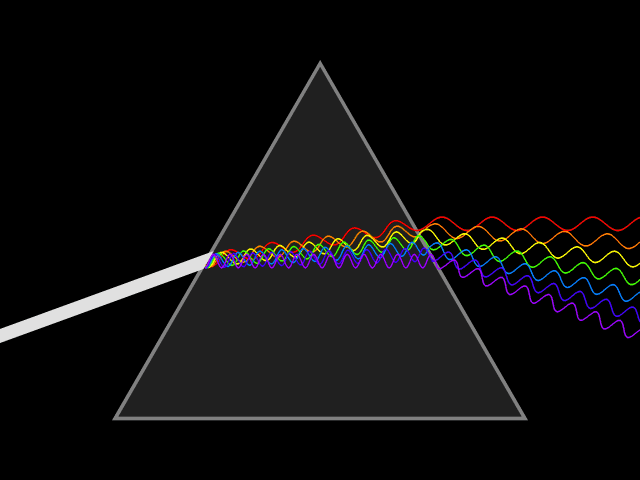
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.


Когда световой луч падает на треугольной призмы в определенном положении, он выходит из призмы, d ispersed в радуги , Есть два типа о е треугольной призмы , которые являются нормальными призму и тонкую призму, но прямоугольная стекло не рассеивается свет, потому что он действует как две похожие перевернутые призмы, одна из которых нейтрализует дисперсию другой.
Нормальная призма
Если луч света падает на грань призмы, он преломляется внутри призмы, пока не упадет на вторую грань и не выйдет из призмы. Луч света преломляется дважды. Луч света отклоняется от своего пути на определенный угол, который называется углом отклонения (α).
Угол отклонения (α) — это угол, образованный направлением распространения падающего луча и выходящего луча в треугольной призме, угол при вершине (A) — это ограниченный угол между двумя сторонами призмы, одна из которых, световой луч падает на него, а другой, световой луч выходит из него.
Когда угол отклонения треугольной призмы = 35 °, это означает, что угол, образованный направлениями распространения падающего и выходящего лучей, = 35 °.
Вывод законов треугольной призмы.
Угол при вершине призмы (A): A = Θ 1 + Φ 2
Где: Θ 1 — угол преломления на первой поверхности, а Φ 2 — угол падения на вторую поверхность.
Угол отклонения (α): α = (Φ 1 — Θ 1 ) + (Θ 2 — Φ 2 )
Где: Φ 1 — угол падения на первую поверхность, а Θ 2 — угол выхода.
α = (Φ 1 + Θ 2 ) — А
Отслеживание пути светового луча в треугольной призме:
Первое: угол падения на первую поверхность (Φ 1 )
Когда Φ 1 > 0 °, луч света преломляется внутри призмы и падает на другую поверхность.
грех Θ 1 = грех Φ 1 / n, A = Θ 1 + Φ 2
Когда Φ 1 = 0 °, луч света проходит без преломления.
Φ 1 = Θ 1 = 0 ° , A = Φ 2
Второе: угол падения на вторую поверхность (Φ 2 ):
Когда Φ 2 > Φ c (критический угол призмы), световой луч полностью отражается внутри призмы.
Угол падения = Угол отражения.
Когда Φ 2 <Φ c , световой луч преломляется и выходит из призмы рядом с разделяющей поверхностью (вдали от нормали).
грех Θ 2 = п грех Φ 2
Третье: угол появления (Θ 2 ).
Когда Θ 2 = 90 °, луч света выходит по касательной к разделяющей поверхности.
Φ 2 = Φ c , A = Θ 1 + Φ c
Когда Θ 2 = 0 °, луч света выходит перпендикулярно противоположной поверхности призмы.
Φ 2 = 2 = 0 °, A = 1
Факторы влияют на угол отклонения треугольной призмы
Согласно соотношению: α = (Φ 1 + Θ 2 ) — A
Угол отклонения в вершине призмы (A) зависит только от угла падения (Φ 1 ) . Угол отклонения уменьшается по мере увеличения угла падения (Φ 1 ) до тех пор, пока он не достигнет своего минимального значения (α o ) и затем снова увеличивается за счет увеличения (Φ 1 ) . Значение (α o ) называется минимальным углом отклонения.
Условия минимального угла отклонения:
- Угол падения (Φ 1) равен углу выхода ( 2 ).
- Угол первого преломления ( 1) равен второму углу падения (Φ 2 ).
Минимальный угол отклонения (α o ) — это наименьший угол отклонения светового луча в призме, при котором угол падения равен углу выхода.
Когда минимальный угол отклонения светового луча в треугольной призме = 30 °, это означает, что это наименьший угол отклонения светового луча в призме, при котором угол падения равен углу выхода = 30 °.
Вычитание показателя преломления призмы, установленного при минимальном угле отклонения:
Когда призма находится в положении минимального отклонения:
Φ 1 = Θ 2 = Φ o , Θ 1 = Φ 2 = Θ o
α o = 2 Φ o — A ∴ Φ o = (α o + A) / 2
А = 2 Θ о ∴ Θ о = А / 2
n = sin Φ o / sin Θ o ∴ n = sin ((α o + A) / 2) / sin (A / 2)
Угол при вершине призмы постоянен. Соответственно, поскольку показатель преломления призмы различается для каждого цвета, минимальный угол отклонения также различается для каждого цвета. Когда α o увеличивается, n также увеличивается, и наоборот. Показатель преломления ( n) зависит от длины волны n ∝ 1 / λ ∴ α o зависит от длины волны.
Рассеяние белого света треугольной призмой:
Белый свет состоит из семи цветов , каждый имеет свою длину волны, Каждый цвет имеет свой угол отклонения. Соответственно, если луч белого света падает на призму, установленную на минимальный угол отклонения, выходящий свет рассеивается на семь спектральных цвета: красный, оранжевый, желтый, зеленый, синий, индиго и фиолетовый (расположены соответственно от вершины призмы к ее основанию).
Фиолетовый цвет имеет максимальное отклонение, максимальный показатель преломления и минимальную длину волны. Красный цвет имеет минимальное отклонение, минимальный показатель преломления и максимальную длину волны.
Тонкая призма
Это треугольная призма из прозрачного материала (стекла) с очень маленьким углом при вершине, не превышающим 10 °, и всегда устанавливается в положение минимального отклонения.Существуют некоторые концепции, связанные с тонкой призмой, такие как угол отклонения, угловая дисперсия и дисперсия. власть .
Угол отклонения
Учет угла отклонения тонкой призмы:
Тонкая призма всегда находится в положении минимального отклонения. Показатель преломления материала призмы можно оценить по соотношению:
п = Sin ((α О + А) / 2) / sin (А / 2)
(α o + A) / 2, A / 2 — малые углы, тогда синус угла равен углу в радианах.
∴ п = (α o + A) / 2 ÷ (A / 2)
п = (α о + А) / А
Α o + A = A n, ∴ α o = A (n — 1)
Факторы, влияющие на угол отклонения тонкой призмы:
- Угол при вершине тонкой призмы (A) прямо пропорционален.
- Показатель преломления его материала (n) прямо пропорционален.
Где α o в тонкой призме не зависит от первого угла падения, тонкая призма всегда находится под минимальным углом отклонения.
Угловая дисперсия
Учет угловой дисперсии в тонкой призме:
Тонкая призма всегда находится в положении минимального отклонения. Она рассеивает белый свет на семь спектральных цветов, где:
Угол отклонения красного света оценивается из соотношения:
(α o ) r = A (n r — 1)
Угол отклонения синего света оценивается из соотношения:
(α o ) b = A (n b — 1)
Где: (n r ) — показатель преломления призмы для красного света, а (n b ) — показатель преломления призмы для синего света.
(α o ) b — (α o ) r = A (n b — n r )
Величина [(α o ) b — (α o ) r ] называется угловой дисперсией между синим и красным лучами.
Угловая дисперсия между синим и красным — это ограниченный угол между расширениями появившихся синего и красного световых лучей после выхода из призмы или разница между углами отклонения синего и красного цветов.
Когда угловая дисперсия между синим цветом и красным цветом = 3 °, это означает, что ограниченный угол между выходящими лучами синего и красного света = 3 °.
Факторы, влияющие на угловую дисперсию:
- Угол при вершине призмы.
- Показатель преломления призмы как для синего, так и для красного цветов.
Желтый цвет считается средним между синим и красным цветом . Средний показатель преломления (n y ) — это средний показатель преломления между синим и красным цветами, Это также показатель преломления желтого света (n y ), n y. = (п б + п г ) / 2.
Среднее отклонение (α o ) y — это среднее отклонение между синим и красным лучами. Это также отклонение желтого света (α o ) y , (α o ) y = ½ × [(α o ) b + (α о ) г ].
Диспергирующая способность
Уменьшение диспергирующей способности:
(α o ) r = A (n r — 1) , (α o ) b = A (n b — 1) .
(α o ) b — (α o ) r = A (n b — n r )
Угол отклонения для желтого света (средний между синим и красным) составляет:
(α o ) y = A (n y — 1)
Где (n y ) — показатель преломления желтого цвета.
Если (α o ) y является средним от (α o ) b и (α o ) r , то (n y ) является средним от (n b ) и (n r ).
ω α = ((α o ) b — (α o ) r ) / (α o ) y
ω α = A (n b — n r ) / A (n y — 1)
ω α = (n b — n r ) / (n y — 1)
Где ω α — дисперсионная способность и может быть определена как:
Дисперсная способность призмы (ω α ) — это отношение угловой дисперсии синего и красного цветов к углу отклонения среднего цвета (желтого).
Когда рассеивающая способность призмы = 0,08, это означает, что отношение угловой дисперсии для синего и красного цветов к углу отклонения желтого цвета = 0,08.
Факторы, влияющие на дисперсионную способность тонкой призмы:
Показатель преломления призмы для синего, красного и желтого цветов.
Ход лучей в призме

Модель наглядно демонстрирует ход лучей в трехгранной призме. Направление падающего луча можно изменять.
Призмы изготавливают из оптического стекла и используют для отклонения лучей света. Рассмотрим ход лучей света в трехгранной призме. Если луч света падает на грань AB и выходит через грань BC, то грань BC называют основанием призмы, см. рис. Противоположный основанию угол γ называют преломляющим углом призмы. Угол Δ между направлением луча 1 и направлением отклонённого луча 2 называется углом отклонения луча в призмы. Угол, на который призма отклоняет (монохроматический) луч света, зависит от преломляющего угла призмы γ, коэффициента преломления призмы n и угла падения α1 (см. рис.)

Рис. Луч 1 падает на грань AB трехгранной призмы, преломляется, падает на грань BC, преломляется и выходит (луч 2) из призмы. При прохождении через призму луч света отклоняется на угол Δ, который зависит от оптической плотности материала призмы n и от преломляющего угла призмы  Показаны нормали n1 и n2 к преломляющим граням призмы. Видно, что луч света, прошедший через призму, отклоняется к основанию AC. При преломлении в точке M углы падения α1 и преломления β1 связаны равенством
Показаны нормали n1 и n2 к преломляющим граням призмы. Видно, что луч света, прошедший через призму, отклоняется к основанию AC. При преломлении в точке M углы падения α1 и преломления β1 связаны равенством
 (1)
(1)
Из треугольника MNB находим угол падения α2 луча на грань призмы BC. Угол  дополняет угол β1 до прямого угла, поэтому
дополняет угол β1 до прямого угла, поэтому

Аналогично, угол  дополняет угол α2 до прямого угла, поэтому
дополняет угол α2 до прямого угла, поэтому
 Поскольку сумма углов в треугольнике равна Π , получаем
Поскольку сумма углов в треугольнике равна Π , получаем
 (2)
(2)
Углы α2 и β2 связаны соотношением
 (3)
(3)
В точке M луч отклоняется на угол α1 и β1, а в точке N – на угол β2 –α2. Поэтому полный угол отклонения луча Δ призмой равен сумме отклонений в точках M и N

Подставляя сюда значение α2 из (2), получаем
 (4)
(4)
Используя равенства (1) – (4) и зная n и γ, можно вычислить угол Δ отклонения луча призмой для каждого угла падения α1 .