Как найти угол отражения луча на границе

Как найти угол отражения луча на границе

На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

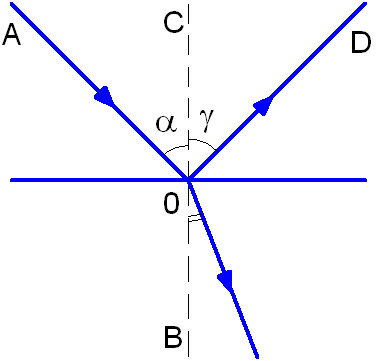
Рис. 1.3. Отражение и преломление света.

Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

1 Падающий луч, отражающий луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости.
2 Угол отражения γ равен углу падения α:

γ = α

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

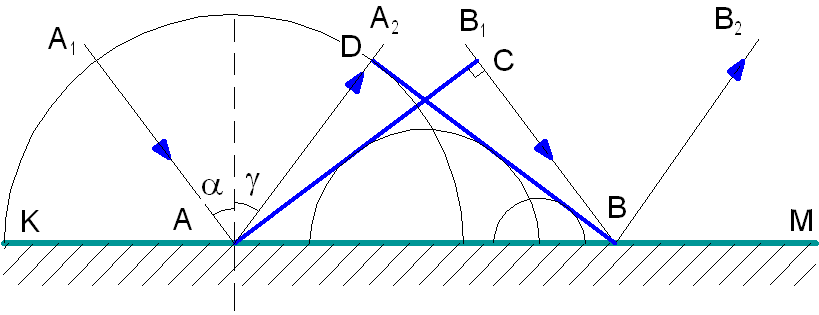
Рис. 1.4. Построение Гюйгенса.

А1А и В1В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА2 и ВВ2.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ.

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

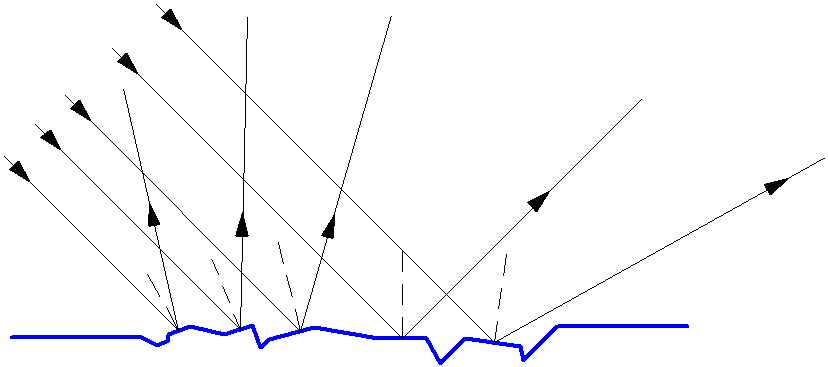
Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

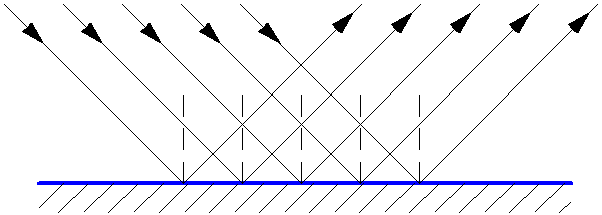
Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

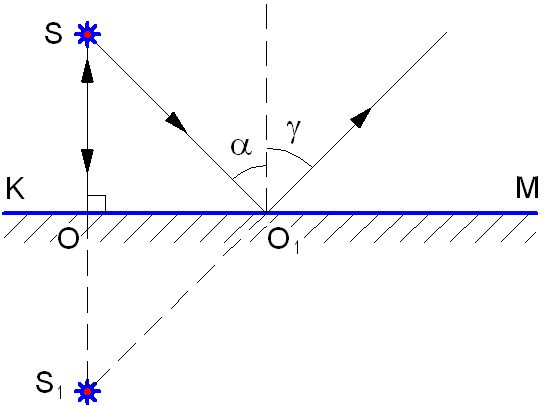
Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO1.

Луч SO1 падает на зеркало под углом α и отражается под углом γ (α = γ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S1, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S1, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S1расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

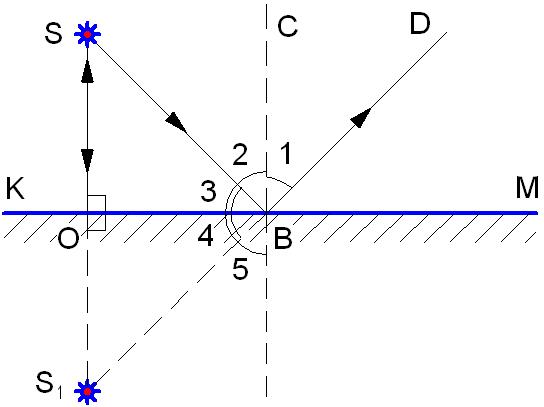
Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS1OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS1, то есть точка S1 расположена симметрично точке S относительно зеркала.

Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

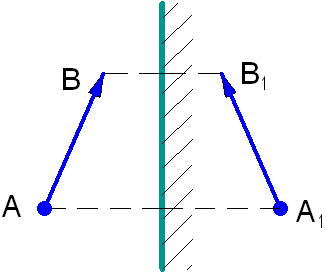
Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Источник

Условие задачи:

Чему равен предельный угол полного внутреннего отражения светового луча на границе раздела двух сред, скорости света в которых равны 108 и 2·108 м/с?

Задача №10.4.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(upsilon_1=10^8) м/с, (upsilon_2=2 cdot 10^8) м/с, (alpha_{пр}-?)

Решение задачи:

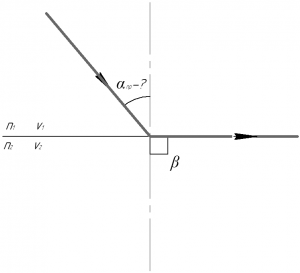Схема к решению задачиПоказатель преломления данной среды относительно вакуума называется абсолютным показателем преломления данной среды (n), его можно определить как отношение скорости света в вакууме (c), равной 3·108 м/с, к скорости света в данной среде (upsilon):

[n = frac{c}{upsilon};;;;(1)]

Из этой формулы можно сделать вывод, что раз ({upsilon_2} > {upsilon_1}), значит ({n_2} < {n_1}), то есть явление полного внутреннего отражения будет наблюдаться при переходе света из среды 1 в среду 2.

Запишем формулу (1) для обеих сред, это пригодится в дальнейшем решении:

[left{ begin{gathered}
{n_1} = frac{c}{{{upsilon _1}}} hfill \
{n_2} = frac{c}{{{upsilon _2}}} hfill \
end{gathered} right.]

Запишем закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения при переходе светового луча из среды 1 в среду 2:

[{n_1}sin alpha_{пр} = {n_2}sin beta]

Здесь (alpha_{пр}) – предельный угол полного внутреннего отражения, (beta) – угол преломления, равный в данном случае 90°, (n_1) и (n_2) – показатели преломления сред. Тогда, так как (sin beta = 1):

[{n_1}sin {alpha _{пр}} = {n_2}]

[sin {alpha _{пр}} = frac{{{n_2}}}{{{n_1}}}]

[{alpha _{пр}} = arcsin left( {frac{{{n_2}}}{{{n_1}}}} right)]

Учитывая систему, записанную выше, имеем:

[{alpha _{пр}} = arcsin left( {frac{{{upsilon _1}}}{{{upsilon _2}}}} right)]

Задача решена, подставим данные задачи в полученную формулу и посчитаем численный ответ:

[{alpha _{пр}} = arcsin left( {frac{{{{10}^8}}}{{2 cdot {{10}^8}}}} right) = 30^circ ]

Ответ: 30°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.4.10 Предельный угол полного внутреннего отражения для бензола 45°. Определить
10.4.12 Предельный угол полного внутреннего отражения в системе скипидар-воздух равен 45°
10.4.13 На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света

Источник

В
общем случае произвольного угла падения
луча на границу раздела двух сред
коэффициент отражения
R
определяется известными формулами
Френеля,
согласно которым он является функцией
значений оптических постоянных этих
двух сред и значения угла падения, а
также зависит от поляризации
падающего луча (понятие поляризации
света предполагается известным
студентам).7

2.2.1.
Отражение
на границе
раздела
двух прозрачных
сред

Формулы
Френеля для отражения на границе
раздела
двух прозрачных
сред
имеют следующий вид.

Для луча,
поляризованного перпендикулярно
плоскости падения:

Rs
=
(2.2.1а)

Для
луча, поляризованного параллельно
плоскости падения:

Rp
= (2.2.1б)

Для
простейшего случая нормального падения
луча из среды c показателем преломления
n1
на границу раздела с полностью прозрачным
(непоглощающим) материалом, имеющим
показатель преломления n2,
формулы Френеля (2.2.1а) и (2.2.1б) сводятся
к одной простой формуле, так как
коэффициент отражения
R
перестает зависеть от вида поляризации
падающего луча:

R
= (n2
–
n1)2
/ (n2
+
n1)2. (2.2.2а)

При
нормальном падении луча из вакуума (n1
= 1) или воздуха (n1

1) уравнение (2.1.5) переходит, при обозначении
n2
просто через n,
в хорошо известную простейшую формулу

R
= (n
-1)2
/ (n
+1)2. (2.2.2б)

Рассмотрим
угловую зависимость коэффициента
отражения на примере границы раздела
двух прозрачных сред со значениями
показателя преломления, равными 1.0
(вакуум или воздух) и 2.0 (см. рис. 9).

Как
видно из рис. 9, при падении луча из
оптически менее плотной среды на
поверхность более плотной коэффициент
отражения
Rs
(для поляризации перпендикулярно
плоскости падения) нелинейно возрастает
с увеличением угла падения. Напротив,
коэффициент отражения
Rp
(для поляризации параллельно плоскости
падения) нелинейно убывает с увеличением
угла падения, проходя через глубокий
(почти до нуля) минимум при определенном
значении угла, называемом углом
Брюстера.8
Для стекла со значением n2
≈ 1.5 в воздухе или вакууме значение угла
Брюстера составляет примерно 56°.

Рис.
9. Угловая зависимость коэффициента
отражения для случаев падения луча (а)
из менее плотной среды (вакуум) в более
плотную (n2
= 2.0) и (б) из той же более плотной среды
в менее плотную (вакуум).

Такое
различное угловое поведение значений
Rs
и Rp
приводит к тому, что при падении пучка
неполяризованного света, характеризуемого
коэффициентом отражения
R
= (Rs
+ Rp)/2,
отраженный и преломленный лучи оказываются
в той или иной степени поляризованными.
В отраженном луче преобладает (или, при
угле Брюстера, полностью доминирует)
s-составляющая
поляризации (этот эффект раньше даже
использовался на практике для создания
поляризаторов за счет многократного
отражения). В
преломленном
луче
преобладает
p-составляющая
поляризации.

Рис.
9 показывает далее, что при падении луча
из оптически более плотной среды на
поверхность менее плотной общая форма
кривых угловой зависимости коэффициентов
отражения
Rs
и
Rp
сохраняется. Однако возрастание обоих
коэффициентов отражения с увеличением
угла происходит гораздо быстрее, и их
значения, равные 1.0 (100%) достигаются не
при нормальном падении, как в предыдущем
случае, а при определенном значении
угла падения 
<< 90°, которое называется критическим
углом или углом полного внутреннего
отражения.9
Для стекла со значением n2
≈ 1.5 в воздухе или вакууме значение
критического угла составляет примерно
41°.

2.2.2.
Отражение
на границе
сильно поглощающего материала

Для
сильно
поглощающего материала (

n)
действительный
показатель преломления n
во всех вышеприведенных соотношениях
должен быть заменен комплексным
показателем преломления
,
что делает их достаточно сложными, В
простейшем случае нормального падения
из вакуума или воздуха соотношение
(2.2.2б) принимает вид

(2.2.3)

Из
уравнения (2.2.3)
видно, что при

n
значение R
стремится к единице (случай зеркального
отражения металлов).

Переходя
к более детальному рассмотрению отражения
на границе сильно поглощающего материала,
необходимо уточнить само понятие
коэффициента отражения. Тот коэффициент
отражения R,
который рассматривался выше, более
точно именуется термином «энергетический
коэффициент отражения». Однако для
полной характеристики отраженного луча
необходимо знать не только его энергию,
но и его фазу. Дело в том, что фаза
отраженного луча остается неизменной
только при отражении от полностью
прозрачного диэлектрика. При наличии
поглощения в материале фаза отраженного
от него луча изменяется тем

больше,
чем выше его показатель поглощения .
Крайним случаем являются металлы (

n),
при отражении от которых фаза отраженного
луча изменяется на
(180).
Таким образом, изменение фазы луча при
отражении от поверхности материала,
обозначаемое обычно термином «фазовый
угол»,
является хотя и непрямой, но вполне
однозначной характеристикой поглощения
в материале. Поскольку
= (),
то и фазовый угол является функцией
частоты падающего излучения. При
измерении энергетического коэффициента
отражения R
информация о значениях фазового угла
(и соответственно о поглощении) теряется.

Полную
информацию об отраженном луче дает
комплексный амплитудный
коэффициент отражения:

, (2.2.4)

где


и
(
)
– фазовый угол. Однако амплитудный
коэффициент отражения не поддается
прямому измерению, и поэтому для
извлечения информации о значениях
фазового угла из экспериментальных
данных требуется достаточно сложная
вычислительная процедура (см. ниже
параграфы 3.2 и 6.1).

Зависимость
комплексного амплитудного коэффициента
отражения от угла падения

дается соответствующими уравнениями
Френеля для перпендикулярно и параллельно
поляризованных пучков:

(2.2.5а)

и

(2.2.5б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Отражение света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон отражения света, построение изображений в плоском зеркале.

Когда световой луч падает на границу раздела двух сред, происходит отражение света: луч изменяет направление своего хода и возвращается в исходную среду.

На рис. 1 изображены падающий луч AO, отражённый луч OB, а также перпендикуляр OC, проведённый к отражающей поверхности KL в точке падения O.

Рис. 1. Закон отражения

Угол AOC называется углом падения. Обратите внимание и запомните: угол падения отсчитывается от перпендикуляра к отражающей поверхности, а не от самой поверхности! Точно так же угол отражения – это угол BOC, образованный отражённым лучом и перпендикуляром к поверхности.

Закон отражения.

Сейчас мы сформулируем один из самых древних законов физики. Он был известен грекам ещё в античности!

Закон отражения.
1) Падающий луч, отражённый луч и перпендикуляр к отражающей поверхности, проведённый в точке падения, лежат в одной плоскости.
2) Угол отражения равен углу падения.

Таким образом, angle AOC=angle BOC, что и показано на рис. 1.

Закон отражения имеет одно простое, но очень важное геометрическое следствие. Давайте посмотрим на рис. 2. Пусть из точки A исходит световой луч. Построим точку {A}, симметричную точке A относительно отражающей поверхности KL.

Из симметрии точек A и {A} ясно, что angle AOK=angle {A}. Кроме того, angle AOK+angle AOC=90^{circ}. Поэтому angle {A}, и, следовательно, точки {A} лежат на одной прямой! Отражённый луч OB как бы выходит из точки {A}, симметричной точке A относительно отражающей поверхности. Данный факт нам чрезвычайно пригодится в самом скором времени.

Закон отражения описывает ход отдельных световых лучей – узких пучков света. Но во многих случаях пучок является достаточно широким, то есть состоит из множества параллельных лучей. Картина отражения широкого пучка света будет зависеть от свойств отражающей поверхности.

Если поверхность является неровной, то после отражения параллельность лучей нарушится. В качестве примера на рис. 3 показано отражение от волнообразной поверхности. Отражённые лучи, как видим, идут в самых разных направлениях.

Рис. 3. Отражение от волнообразной поверхности

Но что значит “неровная” поверхность? Какие поверхности являются “ровными”? Ответ таков: поверхность считается неровной, если размеры её неровностей не меньше длины световых волн. Так, на рис. 3 характерный размер неровностей на несколько порядков превышает величину длин волн видимого света.

Поверхность с микроскопическими неровностями, соизмеримыми с длинами волн видимого света, называется матовой. В результате отражения параллельного пучка от матовой поверхности получается рассеянный свет – лучи такого света идут во всевозможных направлениях. (Именно поэтому мы видим окружающие предметы: они отражают рассеянный свет, который мы и наблюдаем с любого ракурса.)
Само отражение от матовой поверхности называется поэтому рассеянным или диффузным. (Латинское слово diffusio как раз и означает распространение, растекание, рассеивание.)

Если же размер неровностей поверхности меньше длины световой волны, то такая поверхность называется зеркальной. При отражении от зеркальной поверхности параллельность пучка сохраняется: отражённые лучи также идут параллельно (рис. 4)

Рис. 4. Отражение от зеркальной поверхности

Приблизительно зеркальной является гладкая поверхность воды, стекла или отполированного металла. Отражение от зеркальной поверхности называется соответственно зеркальным. Нас будет интересовать простой, но важный частный случай зеркального отражения – отражение в плоском зеркале.

Плоское зеркало.

Плоское зеркало – это часть плоскости, зеркально отражающая свет. Плоское зеркало – привычная вещь; таких зеркал несколько в вашем доме. Но теперь мы сможем разобраться, почему, смотрясь в зеркало, вы видите в нём отражение себя и находящихся рядом с вами предметов.

Точечный источник света S на рис. 5 испускает лучи в разных направлениях; давайте возьмём два близких луча, падающих на плоское зеркало. Мы уже знаем, что отражённые лучи пойдут так, будто они исходят из точки S{} , симметричной точке S относительно плоскости зеркала.

Рис. 5. Изображение источника света в плоском зеркале

Самое интересное начинается, когда расходящиеся отражённые лучи попадают к нам в глаз. Особенность нашего сознания состоит в том, что мозг достраивает расходящийся пучок, продолжая его за зеркало до пересечения в точке S{}. Нам кажется, что отражённые лучи исходят из точки S{} – мы видим там светящуюся точку!

Эта точка служит изображением источника света S Конечно, в реальности ничего за зеркалом не светится, никакая энергия там не сосредоточена – это иллюзия, обман зрения, порождение нашего сознания. Поэтому точка S{} называется мнимым изображением источника S. В точке S{} пересекаются не сами световые лучи, а их мысленные продолжения “в зазеркалье”.

Ясно, что изображение S{} будет существовать независимо от размеров зеркала и от того, находится ли источник непосредственно над зеркалом или нет (рис. 6). Важно только, что-бы отражённые от зеркала лучи попадали в глаз – а уж глаз сам сформирует изображение источника.

Рис. 6. Источник не над зеркалом: изображение есть всё равно

От расположения источника и размеров зеркала зависит область видения – пространственная область, из которой видно изображение источника. Область видения задаётся краями K и L зеркала KL. Построение области видения изображения S{} ясно из рис. 7; искомая область видения выделена серым фоном.

Рис. 7. Область видения изображения источника S

Как построить изображение произвольного предмета в плоском зеркале? Для этого достаточно найти изображение каждой точки этого предмета. Но мы знаем, что изображение точки симметрично самой точке относительно зеркала. Следовательно, изображение предмета в плоском зеркале симметрично предмету относительно плоскости зеркала (рис. 8).

Рис. 8. Изображение предмета AB в плоском зеркале

Расположение предмета относительно зеркала и размеры самого зеркала не влияют на изображение (рис. 9).

Рис. 9. Изображение не зависит от взаимного расположения предмета и зеркала

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Отражение света.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 февраля 2023 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Отражение.

два отражения: от перьев птицы и от воды

Отраже́ние — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения).

В акустике отражение является причиной эха и используется в гидролокации. В геологии оно играет важную роль в изучении сейсмических волн. Отражение наблюдается на поверхностных волнах в водоёмах. Отражение наблюдается со многими типами электромагнитных волн, не только для видимого света: отражение УКВ и радиоволн более высоких частот имеет важное значение для радиопередач и радиолокации. Даже жёсткое рентгеновское излучение и гамма-лучи могут быть отражены на малых углах к поверхности специально изготовленными зеркалами. В медицине отражение ультразвука на границах раздела тканей и органов используется при проведении УЗИ-диагностики.

История[править | править код]

Впервые закон отражения упоминается в «Катоптрике» Евклида, датируемой примерно 300 годом до н. э.

Законы отражения. Формулы Френеля[править | править код]

Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части[1]. Широко распространённая, но менее точная формулировка «угол отражения равен углу падения» не указывает точное направление отражения луча. Тем не менее, выглядит это следующим образом:

Angle.svg

Этот закон является следствием применения принципа Ферма к отражающей поверхности и, как и все законы геометрической оптики, выводится из волновой оптики. Закон справедлив не только для идеально отражающих поверхностей, но и для границы двух сред, частично отражающей свет. В этом случае, равно как и закон преломления света, он ничего не утверждает об интенсивности отражённого света.

Вывод закона

Пусть vec{k} лежит в плоскости чертежа. Пусть ось x направлена горизонтально, ось y — вертикально. Из соображений симметрии следует, что vec{k}, vec{k'} и vec{k''}должны лежать в одной плоскости.

Выделим из падающего луча плоскополяризованную составляющую, у которой угол между {vec {E}} и плоскостью произволен. Тогда если выбрать начальную фазу равной нулю, то

  • E=E_{m}e^{{i(omega t-{vec {k}}{vec {r}})}}=E_{m}e^{{omega t-k_{x}x-k_{y}y}};
  • E'=E'_{m}e^{{i(omega 't-{vec {k'}}{vec {r}})}}=E'_{m}e^{{omega 't-k'_{x}x-k'_{y}y+alpha '}};
  • E''=E''_{m}e^{{i(omega ''t-{vec {k''}}{vec {r}})}}=E''_{m}e^{{omega ''t-k''_{x}x-k''_{y}y+alpha ''}}.

Результирующее поле в первой и второй среде равны соответственно

  • E_{1}=E+E'=E_{m}e^{{omega t-k_{x}x-k_{y}y}}+E'_{m}e^{{omega 't-k'_{x}x-k'_{y}y+alpha '}};
  • E_2 = E'' = E''_m e^{omega'' t - k''_x x - k''_y y + alpha''} .

Очевидно, что тангенциальные составляющие E_1 и E_2 должны быть равны на границе раздела то есть при y=0 .

Тогда

E_m e^{omega t - k_x x - k_y y} + E'_m e^{omega' t - k'_x x - k'_y y + alpha'} = E''_m e^{omega'' t - k''_x x - k''_y y + alpha''}

Для того, чтобы последнее уравнение выполнялось для всех t, необходимо, чтобы omega = omega' = omega'', а для того, чтобы оно выполнялось при всех x, необходимо, чтобы

k_x = k'_x = k''_x Leftrightarrow ksin{alpha} = k'sin{alpha'} = k''sin{alpha''} Leftrightarrow cfrac {omega} {v_1} sin{alpha} = cfrac {omega} {v_1} sin{alpha'} = cfrac {omega} {v_2} sin{alpha''},

где

v_{1} и v_{2} — скорости волн в первой и второй среде соответственно.

Отсюда следует, что alpha = alpha' blacksquare

Сдвиг Фёдорова[править | править код]

Сдвиг Фёдорова — явление малого (меньше длины волны) бокового смещения луча света с круговой или эллиптической поляризацией при полном внутреннем отражении. В результате смещения отражённый луч не лежит в одной плоскости с падающим лучом, как это декларирует закон отражения света геометрической оптики.

Явление теоретически предсказано Ф. И. Фёдоровым в 1954 году, позже обнаружено экспериментально.

Механизм отражения[править | править код]

В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла.

  • При попадании электромагнитной волны (свет) на поверхность диэлектрика: возникают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях (как антенна-диполь). Все эти волны складываются и — в соответствии с принципом Гюйгенса — Френеля — дают зеркальное отражение и преломление[прояснить][источник не указан 2328 дней].
  • При попадании электромагнитной волны (свет) на поверхность проводника: возникают колебания электронов (электрический ток), электромагнитное поле которого стремится компенсировать это воздействие, что приводит к практически полному отражению света.

В зависимости от резонансной частоты колебательных контуров в молекулярной структуре вещества при отражении излучается волна определённой частоты (определённого цвета). Так предметы приобретают цвет. Хотя цвет объекта определяется не только свойствами отражённого света (см. Цветовое зрение и Физиология восприятия цвета).

Виды отражения[править | править код]

θi = θr.
Угол падения равен углу отражения

Отражение света может быть зеркальным (то есть таким, как наблюдается при использовании зеркал) или диффузным (в этом случае при отражении не сохраняется путь лучей от объекта, а только энергетическая составляющая светового потока) в зависимости от природы поверхности.

Зеркальное отражение[править | править код]

Зеркальное отражение света отличает определённая связь положений падающего и отражённого лучей: 1) отражённый луч лежит в плоскости, проходящей через падающий луч и нормаль к отражающей поверхности, восстановленную в точке падения; 2) угол отражения равен углу падения. Интенсивность отражённого света (характеризуемая коэффициентом отражения) зависит от угла падения и поляризации падающего пучка лучей (см. Поляризация света), а также от соотношения показателей преломления n2 и n1 2-й и 1-й сред. Количественно эту зависимость (для отражающей среды — диэлектрика) выражают формулы Френеля. Из них, в частности, следует, что при падении света по нормали к поверхности коэффициент отражения не зависит от поляризации падающего пучка и равен

frac{(n_2 - n_1)^2}{(n_2 + n_1)^2}

В важном частном случае нормального падения из воздуха или стекла на границу их раздела (показатель преломления воздуха = 1,0; стекла = 1,5) он составляет 4 %.

Полное внутреннее отражение[править | править код]

Наблюдается для электромагнитных или звуковых волн на границе раздела двух сред, когда волна падает из среды с меньшей скоростью распространения (в случае световых лучей это соответствует бо́льшему показателю преломления).

С увеличением угла падения i, угол преломления также возрастает, при этом интенсивность отражённого луча растет, а преломленного — падает (их сумма равна интенсивности падающего луча). При некотором критическом значении i = i_k интенсивность преломленного луча становится равной нулю и происходит полное отражение света. Значение критического угла падения можно найти, положив в законе преломления угол преломления равным 90°:

sin{i_k} = n_2/n_1

Диффузное отражение света[править | править код]

При отражении света от неровной поверхности отраженные лучи расходятся в разные стороны (см. Закон Ламберта). По этой причине нельзя увидеть своё отражение, глядя на шероховатую (матовую) поверхность. Диффузным отражение становится при неровностях поверхности порядка длины волны и более. Таким образом, одна и та же поверхность может быть матовой, диффузно-отражающей для видимого или ультрафиолетового излучения, но гладкой и зеркально-отражающей для инфракрасного излучения.

Примечания

  1. ↑ Ландсберг Г.С. Элементарный учебник физики: Учеб. пособие В 3 т. Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика / под ред. Г. С. Ландсберга. — М.: ФИЗМАТЛИТ, 2009. — С. 220 – 221. — 656 с. — ISBN 978-5-9221-0351-0.

Ссылки[править | править код]

  • Внутреннее отражение
  • Уголковый отражатель
  • Принцип Гюйгенса — Френеля
Источник

Добавить комментарий