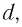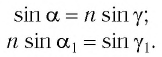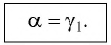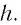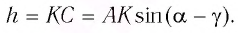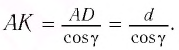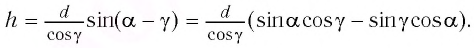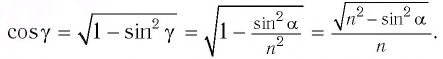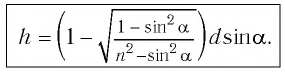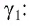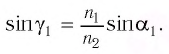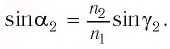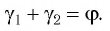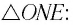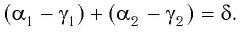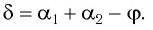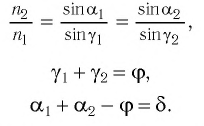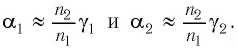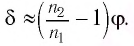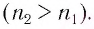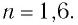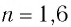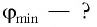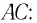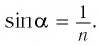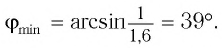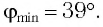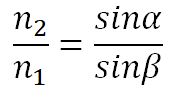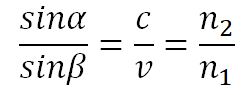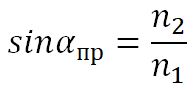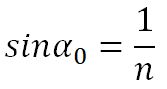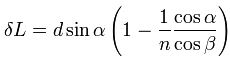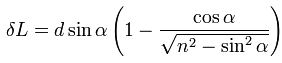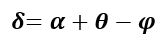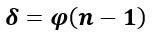В курсе школьной физики изучаются две преломляющие системы:
- плоскопараллельная пластинка
- призма
Плоскопараллельной пластинкой называется оптически прозрачная система (параллелепипед с двумя параллельными гранями). Расстояние между этими двумя плоскостями достаточно мало (рис. 1).
Рис. 1. Плоскопараллельная пластинка
Пусть дана плоскопараллельная пластинка шириной и точечный источник
, из материала с показателем преломления
. Данная плоскопараллельная пластинка помещена в среду с показателем преломления
. От источника под углом
к вертикали падает луч света (на границу раздела сред 1/2). В точке А происходит преломление луча. Далее луч, распространяющийся внутри пластины, падает на вторую границу раздела (в данном случае, 2/1). В точке В также происходит преломление, и луч выходит из системы. Проанализируем ход луча:
- преломление в точке А можно описать законом Снеллиуса:
(1)
- за счёт параллельных граней пластинки, в точку В луч падает под тем же углом
(накрест лежащие углы)
- преломление в точке В также можно описать законом Снеллиуса:
(2)
Т.е. анализ прохождения луча основывается на законах преломления. Избавимся в соотношениях (1) и (2) от параметров второй среды (пластинки), тогда:
(3)
Или, сократив:
(4)
Из соотношения (4) можно сделать вывод, что , что говорит о том, что луч, проходя плоскопараллельную пластинку, выходит из неё под тем же углом (угол падения на пластинку равен углу выхода из пластинки). Таким образом, плоскопараллельная пластинка не меняет направления распространения луча, а смещает его. Для характеристики смещения луча относительно первоначального направления —
(рис. 2).
Призмой называется оптически прозрачная система в форме геометрического тела — призмы, которая имеет плоские полированные грани, через которые входит и выходит свет.
Рис. 2. Призма
Одним из параметров призмы являются преломляющий угол призмы () — угол между гранями на призмы, на одну из которых луч света падает, с другой грани уходит. В основном, задачи на призму касаются угла отклонения луча (
), т.е. угла между падающим лучом (его продолжением) и лучом, выходящим из призмы (его продолжением). Тогда для призмы выведено соотношение:
(5)
Вывод: для оптических систем достаточно прорисовать ход лучей через систему (исходя из законов преломления). А далее, с помощью рисунка, найти необходимые в задаче элементы чаще всего с помощью закона Снеллиуса и геометрических соотношений.
Содержание:
Прохождение света через плоскопараллельные пластинки и призмы:
Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы.
Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые, создают различные оптические приборы. Рассмотрим отдельные элементы оптических приборов.
Плоскопараллельная пластинка
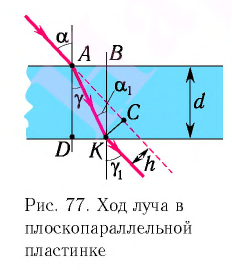
Рассмотрим ход луча в плоскопараллельной пластинке. На рисунке 77 показан ход светового луча в плоскопараллельной пластинке толщиной
Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 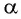
Здесь 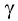
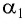
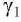
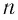
Накрест лежащие углы 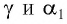
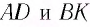

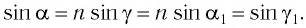
Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению на некоторое расстояние
Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут также казаться смещенными.
Найдем, от каких параметров пластинки зависит смещение 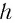
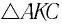
Из 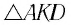
Отсюда:
С учетом закона преломления 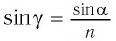
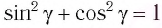
Расстояние 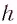
Как видно из соотношения (2), смещение 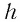
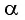
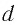
Трехгранная призма
Рассмотрим ход луча в трехгранной призме. Пусть световой луч 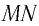
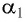
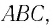
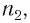
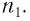
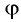
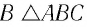
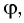
Пусть луч 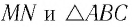
Если показатель призмы 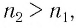
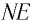
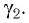
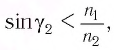
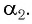
Отклонение от начального направления луча 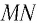
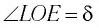
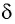
Рассмотрим 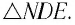
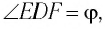
Применим эту же теорему к
Из формул (5) и (6) определим связь угла падения 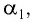
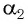
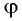
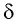
В результате получим систему уравнений (3), (4), (5), (7):
Система уравнений (8) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.
- Заказать решение задач по физике
Если угол падения 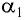
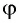
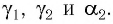
Подставляя полученные выражения для 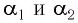
Из соотношения (9) следует, что, во-первых: чем больше преломляющий угол 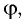
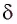
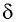
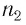
Пример решения задачи
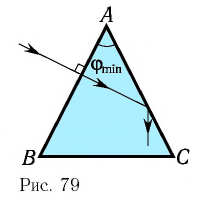
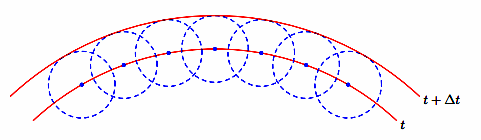
Определите наименьший преломляющий угол 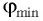
Дано:
Решение:
Запишем условие полного отражения на боковой грани
Вследствие того, что 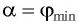
Ответ:
- Поляризация света
- Линзы в физике
- Глаз как оптическая система
- Звук в физике и его характеристики
- Электромагнитная природа света
- Интерференция света
- Дифракция света
- Принцип Гюйгенса — Френеля
-
Преломление в плоскопараллельной пластине
И
плоскопараллельную пластину толщиной
d из материала с
абсолютным показателем преломления
n, на которую падает
из воздуха под углом i
узкий луч света (рис. 5.3). На первой и
второй гранях
Перемножим
почленно эти равенства:
Но
как
внутренние накрест лежащие углы при
параллельных прямых и секущей.
Следовательно,
Тогда
(для
острых углов). Значит, выходящий луч
параллелен падающему, и плоскопараллельная
пластина смещает его на h.
Из
(угол между AK
и
AM
равен i
как один из вертикальных). Из
,
отсюда
По
известным тригонометрическим формулам
-
П
роведите
анализ полученного выражения. Как
зависит смещение h от
толщины пластины, угла падения и
показателя преломления?
-
Преломление в трехгранной призме
И
воздуха падает луч на грань трехгранной
призмы (рис. 5.4, а).
Призма сделана из материала оптически
более плотного, чем окружающая среда.
Если бы не было призмы, луч через точку
М
прошел бы прямолинейно. Но в точке М
он испытывает преломление на границе
с оптически более плотной средой,
поэтому идет под углом преломления
меньшим, чем угол падения. На грани СВ
в точке N
луч снова преломляется, но на этот раз
на границе с оптически менее плотной
средой, так что угол преломления больше
угла падания. Таким образом, луч оба
раза при преломлении откланяется в
одну сторону на суммарный угол отклонения
δ
– угол между входящим и выходящим
лучами. Грани призмы, на которых луч
испытал преломление, называются
преломляющими гранями. Двугранный угол
С
между преломляющими гранями –
преломляющий угол. Грань, на которую
опирается угол С называется основанием
призмы. Итак, если призма сделана из
материала оптически более плотного,
чем окружающая среда, то при преломлении
луч дважды отклоняется в сторону
основания. Если она сделана из материала
оптически менее плотного, чем окружающая
среда, то наоборот. Постройте самостоятельно
ход лучей в такой призме.
-
О
пределите
угол, на который отклонится луч света
в призме с преломляющим углом α,
подающий на одну из ее граней под углом
i.
-
Линзы
В
к рис. 5.4, а и мысленно отрежем нижнюю
и верхнюю часть призмы, не подходя
близко к точкам преломления М и N
(рис. 5.4, б). Для данного луча ничего
не изменится, только теперь усеченная
призма имеет два основания – большее
и меньшее. Дважды преломляясь на границах
усеченной призмы, луч оба раза отклоняется
в сторону большего основания (если
призма сделана из материала, оптически
более плотного, чем окружающая среда).
Сконструируем
систему призм, как показано на рис. 5.5,
и направим на нее параллельный пучок
лучей. Не входя в подробности преломления,
мы знаем его результат. Лучи, пройдя
через призмы, отклоняются в сторону
больших оснований, а так как такие
основания расположены ближе к оси
пучка, параллельные лучи соберутся в
какое-то пятно около этой оси. Не надо
думать, что они соберутся в точку, но
сам факт сближения лучей должен быть
понятен. Такая собирательная система
помимо сложности изготовления и
использования имеет принципиальный
недостаток – много лучей проходит
между призмами, не преломляясь. Можно
заполнить промежутки, одновременно
упростив конструкцию, если взять кусок
стекла и отшлифовать его по сферическим
поверхностям. Такие сферические
стекла или линзы3
широко применяются в оптике. Сферическое
стекло – отшлифованная стеклянная
пластина, ограниченная сферическими
или плоскими поверхностями. Середина
такой линзы практически представляет
собой плоскопараллельную пластину.
Лучи, идущие под углом, отличным от
нуля, в такой пластинке смещаются на h
(см. рис. 5.3). Но это смещение будет
пренебрежимо малым, если ограничится
параксиальными (приосевыми) лучами и
сделать линзу достаточно тонкой.
Тогда любой луч (из выбранных параксиальных)
пройдет через точку О (рис. 5.6),
практически не отклоняясь. Точка, через
которую лучи проходят, не отклоняясь,
называется оптическим центром линзы.
В
се
прямые, проходящие через оптический
центр, – оптические оси. Одна из
оптических осей, проходящая и через
центр сферической поверхности, называется
главной (ограничимся случаем
центрированных систем, в которых
центры кривизны всех поверхностей
лежат на одной прямой). Остальные
оптические оси – побочные.
Параллельный
пучок лучей (естественно, параллельный
и одной из оптических осей, рис. 5.6) после
преломления в данной линзе собирается
приблизительно в одной точке, называемой
действительным фокусом. Такие линзы
называются собирающими. Как мы
видели, собирающими будут выпуклые
линзы (у которых середина толще краев),
если они сделаны из материала, оптически
более плотного, чем окружающая среда.
Параллельный пучок лучей после
преломления в линзе может рассеиваться
(рис. 5.7), тогда в одной точке, называемой
мнимым фокусом, соберутся продолжения
этих лучей. Такие линзы называются
рассеивающими.
Сделанные
из материала, оптически более плотного,
чем окружающая среда, они вогнуты
(середина тоньше краев). Если линзы
сделаны из материала менее плотного,
чем окружающая среда (например, пустотелые
линзы в воде), собирающими будут вогнутые,
а рассеивающими – выпуклые. Проверьте
это построением. Все фокусы, расположенные
по одну сторону линзы, лежат в одной
плоскости, перпендикулярной главной
оптической оси и проходящей через
главный фокус. Она называется фокальной
плоскостью.
Изображением
точки S в линзе будет
точка пересечения всех
преломленных лучей или их продолжений.
В первом случае изображение будет
действительное, во втором – мнимое.
Как всегда, чтобы найти точку пересечения
всех лучей, достаточно построить любые
два. Мы можем это сделать, пользуясь
формулой для второго закона преломления.
Но такая работа достаточно трудоемкая,
поэтому ее обычно избегают. По известным
свойствам линз можно построить три
луча без всяких вычислений. Луч, падающий
параллельно какой-либо оптической оси,
после двойного преломления пройдет
через действительный фокус или его
продолжение пройдет через мнимый фокус.
По закону обратимости луч, падающий по
направлению на соответствующий фокус,
после двойного преломления выйдет
параллельно определенной оптической
оси. Наконец, через оптический центр
линзы луч пройдет, не отклоняясь.
Н
а
рис.5.8 построено изображение точки S
в собирающей линзе, на рис. 5.9 – в
рассеивающей. При таких построениях
изображают главную оптическую ось и
на ней показывают фокусные расстояния
F (расстояния от
главных фокусов или от фокальных
плоскостей до оптического центра линзы)
и двойные фокусные расстояния (для
собирающих линз). Затем ищут точку
пересечения преломленных лучей (или
их продолжений), используя любые два
из вышеперечисленных.
О
вызывает затруднение построения
изображения точки, расположенной на
главной оптической оси. Для такого
построения нужно взять любой луч,
который будет параллелен какой-то
побочной оптической оси (пунктир на
рис. 5.10). После двойного преломления он
пройдет через побочный фокус, который
лежит в точке пересечения этой побочной
оси и фокальной плоскости. В качестве
второго луча удобно использовать луч,
идущий без преломления вдоль главной
оптической оси.
На рис.
5.11 изображены две собирающие линзы.
Вторая «лучше» собирает лучи, ближе их
сводит, она «сильнее». Оптической
силой линзы называется величина,
обратная фокусному расстоянию:
.
Выражается оптическая сила линзы в
диоптриях (дптр). Одна диоптрия
равна оптической силе линзы,
фокусное расстояние которой 1 м. У
собирающих линз положительная оптическая
сила, у рассеивающих – отрицат
ельная.
Построение
изображения предмета в собирающей
линзе сводится к построению его крайних
точек. В качестве примера выберем
стрелку АВ
(рис. 5.12).
Изображение точки А
построено так, как показано на рис. 5.8,
точка В1
может быть найдена так, как показано
на рис. 5.10. Ведем обозначения: расстояние
от предмета до линзы
расстояние от линзы до изображения
фокусное расстояние
Из подобия треугольников
и
(по равным острым углам прямоугольные
треугольники подобны) следует, что
Из подобия треугольников
и
(по тому же признаку подобия) –
Следовательно,
Разделив
уравнение почленно на dFf
и перенеся отрицательный член в другую
сторону равенства, получим
Мы
вывели формулу тонкой линзы. В этой
формуле d, f
и F рассматриваются
как алгебраические величины, знак
которых может быть разным в разных
случаях. При этом возможны всего три
случая, представленные в таблице.
|
Собирающие линзы |
|
|
d>F |
d<F |
|
1. d>0, F>0, Изображение |
2. d>0, Изображение мнимое |
|
Рассеивающие |
|
|
3. d>0, F<0, Изображение |
-
Н
а
каком расстоянии от собирающей линзы
надо поместить предмет, чтобы расстояние
от предмета до его действительного
изображения было наименьшим?
Линейным увеличением линзы называется
число, показывающее, во сколько раз
линейные размеры изображения больше
линейных размеров предмета. Из подобия
рассмотренных треугольников (рис.5.12)
имеем
-
П
очему
на фотографиях, сделанных в инфракрасных
лучах, зелёная растительность получается
белой?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные законы геометрической оптики были известны задолго до установления физической природы света. Большая часть из них выводятся из общего принципа, описывающего поведение волн. Впервые этот принцип выдвинул современник Ньютона Христиан Гюйгенс.
Принцип Гюйгенса
Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.
Чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t + ∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Этот принцип подходит для описания волн любой природы (световых, механических, электромагнитных и пр.).
Для механических волн принцип Гюйгенса имеет наглядное толкование: частицы среды, до которых доходят колебания, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.
Закон прямолинейного распространения света
В оптически однородной среде свет распространяется прямолинейно.
Опытным доказательством этого закона служат резкие тени, отбрасываемые непрозрачными телами при освещении светом источника небольших размеров («точечного источника»).
Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет.
Внимание!
Законы геометрической оптики выполняются приближенно при условии, что размеры препятствий на пути световых волн много больше длины волны. Так, закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через очень малые отверстия.
Пример №1. Здание, освещенное солнечными лучами, отбрасывает тень длиной L = 36 м. Вертикальный шест высотой h = 2,5 м отбрасывает тень длиной l = 3 м. Найдите высоту H здания.
Так как шест и здание расположены вертикально, они параллельны. Так как на них светит один и тот же источник света, то угол падения лучей одинаков. Следовательно, треугольники, образованные стеной зданий, лучом солнца и землей, а также землей, лучом солнца и шестом, подобны. Отсюда можно сделать вывод, что отношение высоты здания к высоте шеста будет отношению длины тени здания к длине тени шеста:
Hh=Ll
H2,5=363=12
H=12·2,5=30 (м)
Закон отражения света
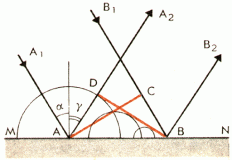
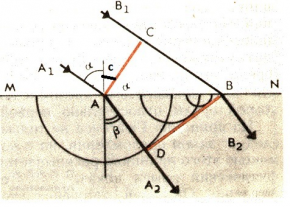
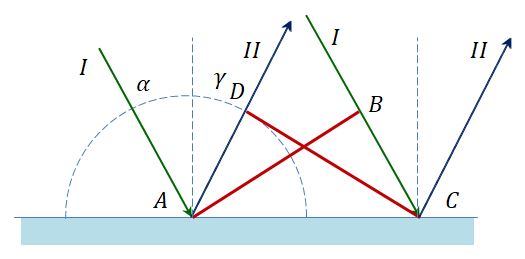
Рассмотрим отражение плоской волны (см. рис. ниже).
Пусть:
- MN — отражающая поверхность.
- A1A и B1B — два параллельных луча падающей плоской волны.
- AC — волновая поверхность плоской волны.
- α и γ— угол падения и отражения лучей A1A и B1B.
Определение
Плоская волна — волна, волновые поверхности которой представляют собой плоскости.
Угол падения — угол между падающим лучом и перпендикуляром к отражающей поверхности.
Угол отражения — угол между перпендикуляром к отражающей поверхности и отраженным лучом.
Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности AC достигают отражающей границы неодновременно. Возбуждение колебаний в точке A начинается раньше, чем в точке B, на время Δt=CBv (v — скорость волны).
В момент, когда волна достигнет точки B, и в этой точке начнется возбуждение колебаний, вторичная волна в точке A уже будет представлять собой полусферу радиусом r = AD = v∆t = CB. Радиусы вторичных волн от источников, находящихся между точками A и B, меняются так, как показано на рисунке выше.
Огибающей вторичных волн является плоскость DB, касательная к сферическим поверхностям. Она является волновой поверхностью отраженной волны. Отраженные лучи AA2 и BB2 перпендикулярны волновой поверхности DB. Между ними образуется угол γ, являющийся углом отражения.
Так как AD = CB и треугольники ADB и ACB прямоугольные, то углы DBA и CAB равны. Но угол α= ∠CAB, а γ= ∠DBA как углы с перпендикулярными сторонами. Следовательно, α=γ.
Закон отражения света
Угол падения равен углу отражения. Падающий луч, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
Пример №2. Луч света падает на плоское зеркало. Угол падения α равен 20°. Чему равен угол между падающим и отражённым лучами?
Поскольку, согласно закон отражения света, угол падения равен углу отражения, то угол между падающим и отражённым лучами равен удвоенному углу α. Следовательно, он равен 40°.
Закон преломления света
На границе двух разнородных сред свет меняет направление распространения. Часть его энергии возвращается в первую среду, то есть, происходит отражение света. Если же вторая среда прозрачна, то часть света проходит через границу, разделяющую первому и вторую среду. При этом он меняет свое направление. Это явление называется преломлением света.
Преломление света на границе двух сред легко продемонстрировать с помощью стакана, воды и карандаша. Если опустить карандаш в пустой стакан, то он будет выглядеть таким же прямым, как и всегда (см. рисунок слева). Если же опустить карандаш в стакан, заполненный водой, мы увидим, что его часть под водой будто бы «преломилась».
Закон преломления света, который определяет взаимное расположение луча падающего, луча преломленного и перпендикуляра, восстановленного в точке падения, был открыт опытным путем в XVII веке. Но его можно доказать, основываясь на принципе Гюйгенса.
Известно, что скорость света достигает максимального значения только в вакууме. При распространении в среде скорость света снижается. Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость распространения волны в первой среде как v1, а во второй — как v2.
Пусть на плоскую границу раздела двух сред (к примеру, из воздуха в воду) падает плоская световая волна (см. рисунок выше). Волновая поверхность AC перпендикулярна лучам A1A и B1B. Поверхности MN сначала достигнет луч A1A. B1B достигнет ее через некоторое время, которое можно определить отношением:
Δt=CBv1
В момент, когда вторичная волна в точке B только начинает возбуждаться, волна от точки A уже имеет вид полусферы, радиус которой определяется выражением:
AD=v2Δt
Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае, ею является плоскость BD. Она является огибающей вторичных волн.
Угол падения α равен CAB в треугольнике ABC (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно:
CB=v1Δt=ABsinα
Угол преломления β равен углу ABD в треугольнике ABD. Поэтому:
AD=v2Δt=ABsinβ
Поделим первое выражение на второе и получим:
sinαsinβ=v1v2=n
Закон преломления света
Падающий луч, луч преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред.
Пример №3. Угол падения параллельных лучей на плоскопараллельную пластинку равен 60о. Найдите расстояние между точками, в которых из пластины выходят параллельные лучи, если расстояние между лучами, прошедшими сквозь пластину, равно 0,7 м.
Сначала построим рисунок хода лучей до пластины, внутри нее и после нее. Расстояние между лучами, прошедшими сквозь пластину, обозначим за l. Оно равна длине перпендикуляра, соединяющего эти лучи.
Значение величины угла β, который составляет нормаль к пластине и направлением распространения луча в ней, определяется законом преломления света:
sinαsinβ=n
Луч выходит из пластины под некоторым углом γ таким, что:
sinβsinγ=1n
Следовательно:
n=sinγsinβ=sinαsinβ
Отсюда: sinγ=sinα или γ= α. Если вспомнить геометрические законы, можно сделать вывод, что расстояние между пластинами, являющееся гипотенузой прямоугольного треугольника, можно вычислить путем деления катета на косинус угла между ним и гипотенузой:
L=lcos60°=0,70,5=1,4 (м)
Величина n — относительный показатель преломления.
Физический смысл показателя преломления заключается в том, что он равен отношению скоростей света в средах, на границе между которыми происходит преломление.
n=v1v2
Различают также абсолютный показатель преломления — показатель преломления среды относительно вакуума. Он равен синусу угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.
Поскольку в вакууме скорость света максимальна, абсолютный показатель преломления можно выразить формулой:
n=cv1
где v1 — скорость света в среде, c — скорость света в вакууме.
Между абсолютными и относительными показателями преломления есть взаимосвязь. Пусть скорость распространения света в первой среде равна v1, во второй — v2. Тогда абсолютные показатели преломления для первой и второй среды равны:
n1=cv1
n2=cv2
Тогда относительный показатель преломления при переходе света из первой среды во вторую будет равен отношению абсолютного показателя преломления второй среды к абсолютному показателю преломления первой среды:
n=v1v2=n2n1
Внимание!
Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой, а среду с большим абсолютным показателем преломления — оптически более плотной.
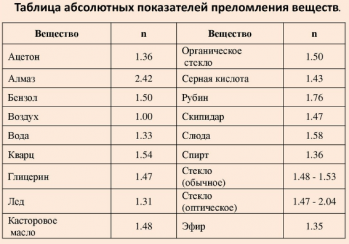
Пример №4. Определить показатель преломления воды относительно алмаза.
n=nвnа
Абсолютные показатели преломления воды и алмаза — постоянные табличные величины.
n=1,332,42≈0,55
Полное отражение
Закон преломления света позволяет объяснить интересное и практически важное явление — полное отражение света.
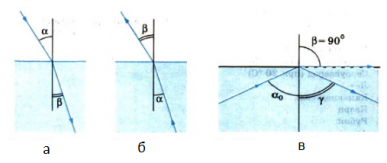
При прохождении света из оптически менее плотной среды в более плотную, к примеру, из воздуха в стекло или воду, v1>v2. Следовательно, согласно закону преломления показатель преломления n > 1. Поэтому α > β (см. рисунок а). В результате преломления луч приближается к перпендикуляру, восстановленному к точке падения луча.
Если же направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль ранее преломленного луча (см. рисунок б), то закон преломления запишется следующим образом:
sinαsinβ=v2v1=1n
Преломленный луч по выходе из оптически более плотной среды будет направлен по линии ранее падавшего луча, поэтому α < β, т. е. преломленный луч в этом случае отдаляется от перпендикуляра, восстановленного в точке падения к границе раздела сред. По мере увеличения угла α угол преломления β также увеличивается. При этом, согласно закону преломления света, он всегда будет больше угла α. Наконец, при некотором угле падения α значение угла преломления β приблизится к 90°, и преломленный луч будет направлен почти по границе раздела двух сред (см. рисунок в). Наибольшему возможному углу преломления β = 90° соответствует угол падения α0.
Попробуем выяснить, что произойдет при α > α0. При падении света на границу двух сред световой луч, как мы уже говорили ранее, частично отражается и частично преломляется. Но при α > α0 преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.
Примеры полного отражения света:
- блеск от ограненного алмаза;
- блеск капель росы на солнце;
- внутреннее отражение предметов, находящихся под водой.
Определение
Угол полного отражения — угол падения α0, соответствующий углу преломления 90°.
При sin β = 1 (что соответствует углу 90°) угол полного отражения можно определить по формуле:
sinα0=1n
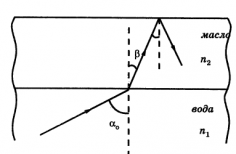
Пример №5. Луч света, идущий из толщи воды, полностью отражается от ее поверхности. Выйдет ли луч в воздух, если на поверхность воды налить слой кедрового масла?
Синус угла полного отражения для луча, идущего из воды к воздуху:
sinα0=1n1
sinα0 n1=1
где n1 — показатель преломления воды.
Запишем закон преломления света для случая, когда на поверхность воды налито масло:
Тогда синус угла полного отражения для луча, идущего из воды к маслу:
sinα0sinβ=n2n1
где n2 — показатель преломления масла.
Тогда:
sinβ=1n2
Эта формула соответствует случаю, когда угол β является углом полного отражения. Следовательно, луч света за пределы масляной пленки в воздух не выйдет.
Практическое применение явления полного отражения света
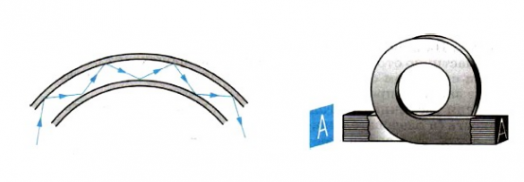
Явление полного отражения света применяют в волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод — это стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления.
За счет многократного полного отражения свет может быть направлен, либо по прямому, либо по изогнутому пути (см. рисунок слева). Волокна собираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (см. рисунок справа). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.
В последнее время волоконная оптика широко используется для быстрой передачи компьютерных сигналов. По волоконному кабелю передается модулированное лазерное излучение.
Задание EF17610
Ученик провёл опыт по преломлению монохроматического света, представленный на фотографии.
Затем вся установка была помещена в воду. Как изменятся частота световой волны, длина волны, падающей на стекло, и угол преломления?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Описать эксперимент, проведенный учеником.
2.Установить, как изменяется частота световой волны при перемещении установки из воздуха в воду.
3.Установить, как при этом изменяется длина световой волны.
4.Установить, как при этом изменяется угол преломления.
Решение
Ученик направил луч монохроматического света на стекло под углом 30 градусов к нормали. При этом луч вышел под углом 20 градусов. Это говорит о том, что свет из менее плотной оптической среды попал в более плотную.
Частота световой волны — характеристика, не зависящая от условий распространения этой волны. Поэтому при перемещении установки из воздуха в воду частота останется прежней.
Чтобы установить, как меняется длина световой волны и угол преломления. Нужно рассчитать изменение показателя преломления света. Относительный показатель преломления в первом и втором опыте будет соответственно равен:
sinαsinβ=nвоздух−стекло
sinαsinγ=nвода−стекло
Относительные показатели преломления можем выразить через абсолютные:
nвоздух−стекло=nстеклоnвоздух
nвода−стекло=nстеклоnвода
Абсолютный показатель преломления — табличная величина. Мы возьмем приблизительный значения: для воздуха — 1, для воды — 1,33, для стекла — 1,5. В действительности абсолютный показатель преломления стекла может составлять от 1,43 до 2,17. Но это не столь важно, поскольку важно лишь то, что он в любом случае больше абсолютного показателя преломления воды.
Получим:
nвоздух−стекло=1,51=1,5
nвода−стекло=1,51,33≈1,3
Видно, что при перемещении из воздуха показатель преломления уменьшился. Тогда:
sinαsinγ=1,3
Так как числитель в левой части уравнения остался прежним, а число в правой части уменьшилось, то синус угла преломления увеличился. Поскольку синус угла находится в прямой зависимости от величины угла, то и угол преломления увеличился.
Длина волны определяется формулой:
λ=vν
Учтем, что скорость распространения света в более плотной среде уменьшается. Если скорость уменьшилась, то длина воды тоже уменьшилась, поскольку между ними существует прямо пропорциональная зависимость.
Ответ: 321
pазбирался: Алиса Никитина | обсудить разбор
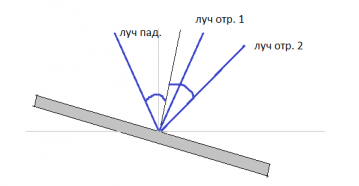
Задание EF18593
Алгоритм решения
1.Записать известные данные.
2.Зарисовать рисунок после поворота зеркала.
3.Представить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
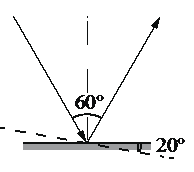
• Угол между падающим и отраженным углом: γ1 = 60о.
• Угол поворота угла: φ = 20о.
Построим рисунок с учетом того, что зеркало повернули:
Поскольку угол падения, равен углу отражения, то:
α1+β1=60°
α1=β1
2α1=60°
α1=60°2=30°
На рисунке видно, что после переворачивания зеркала угол падения α увеличился на угол переворота:
α=α1+φ=30°+20°=50°
Так как угол падения равен углу отражения, то:
α=β=50°
Отсюда угол между лучом падающим и лучом отраженным равен:
γ=α+β=50°+50°=100°
Ответ: 100
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19015
На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.
Алгоритм решения
1.Записать исходные данные.
3.Записать закон полного отражения.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Радиус круглого плота: R = 2,4 м.
• Показатель преломления воды: n = 4/3.
Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.
Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:
sinα=1n
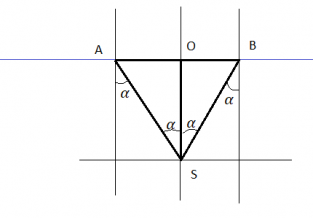
Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.
Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.
Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:
H=Rcotα
Котангенс угла определяется как отношение косинуса этого угла к его синусу:
cotα=cosαsinα
Косинус угла можем выразить из основного тригонометрического тождества:
sin2α+cos2α=1
Следовательно:
cosα=√1−sin2α
Отсюда котангенс равен:
cotα=√1−sin2αsinα
Тогда глубина бассейна:
H=Rcotα=R√1−sin2αsinα
Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:
H=R√1−(1n)21n=Rn√1−1n2
Подставим известные данные и получим:
H=2,4·43⎷1−1(43)2=3,2√1−916=3,2√74≈0,8·2,65=2,12 ⎛⎜⎜⎝м⎞⎟⎟⎠
Ответ: 2,12
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.2k
Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
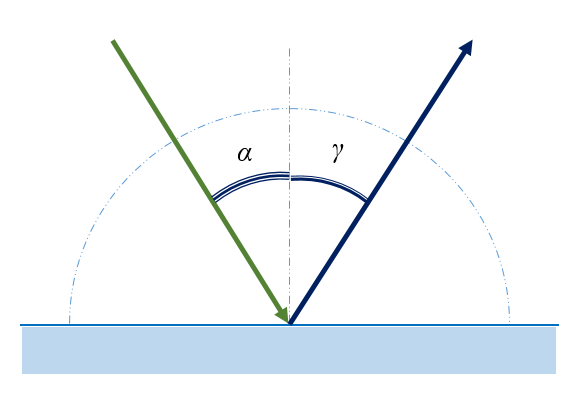
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
Вывод на основе принципа Гюйгенса:
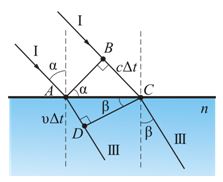
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
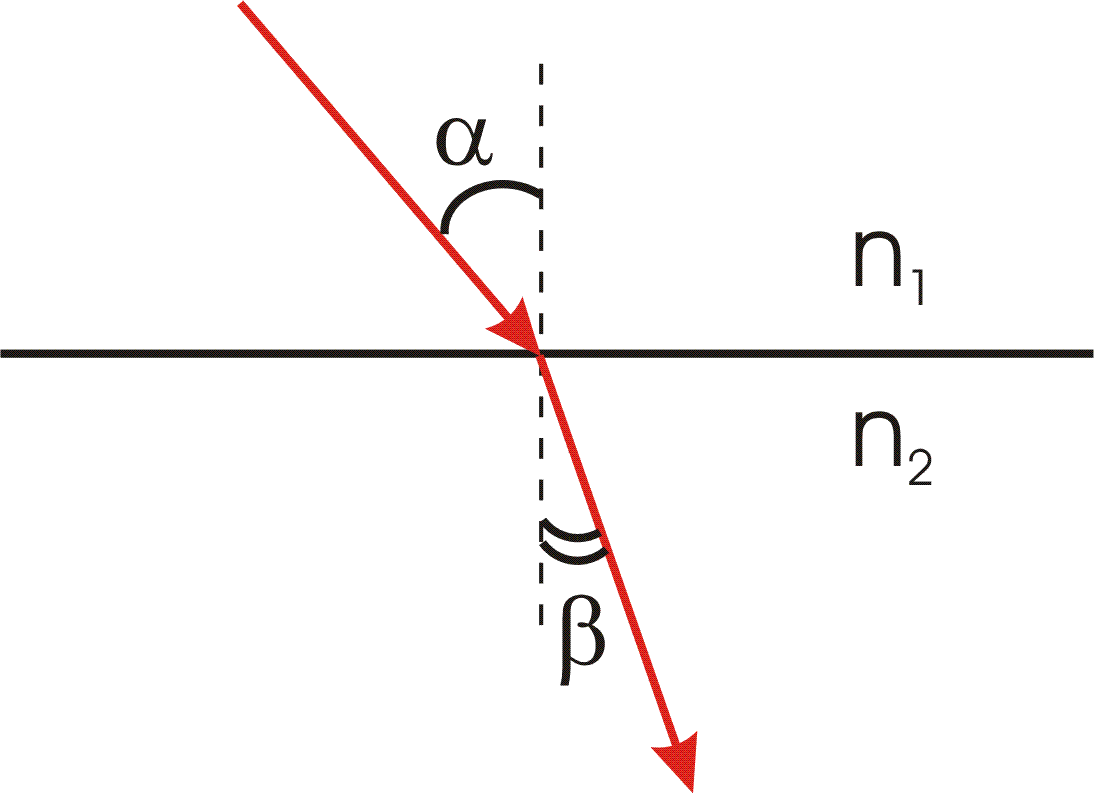

Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что


Отсюда следует закон Снелиуса:
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: 
Следствия из принципа Ферма:
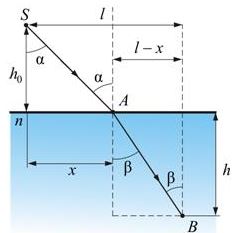
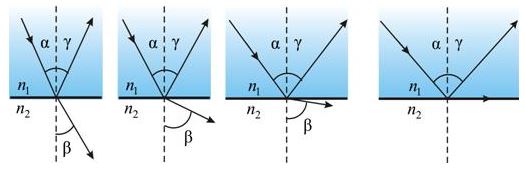
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда – воздух
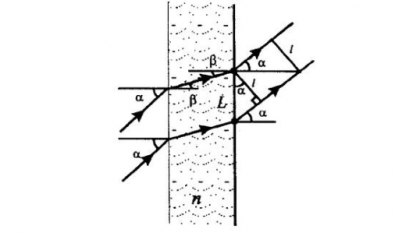
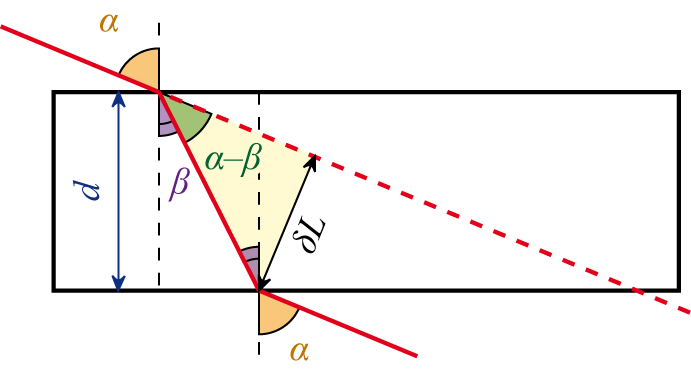
Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
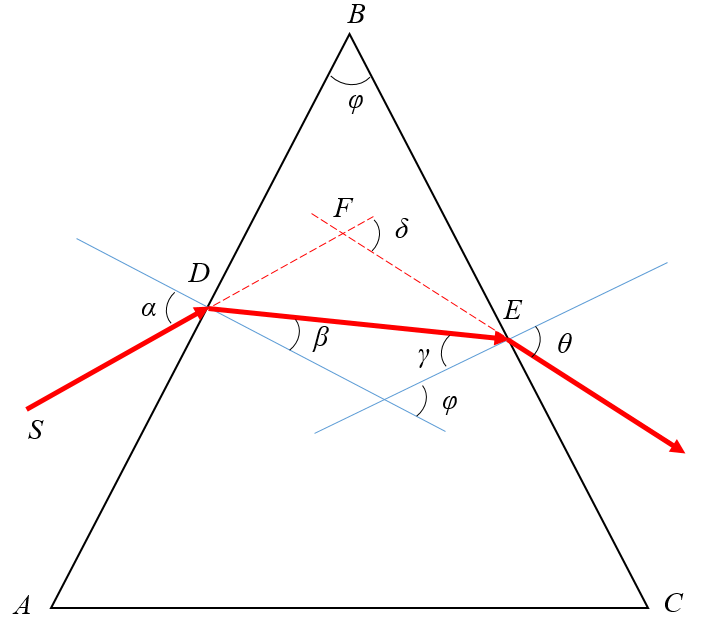
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.