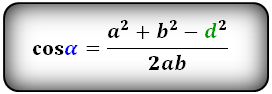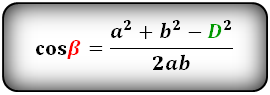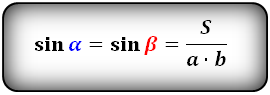Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Частными
случаями параллелограмма являются прямоугольник и ромб. Квадрат одновременно является частным
случаем и прямоугольника и ромба, поэтому все выявленные для параллелограмма зависимости справедливы
для прямоугольника, квадрата и ромба.
На практике необходимость определения угла между диагоналями на основе прочих элементов может
возникнуть, в частности, при необходимости производства построений на местности и для перепроверки
уже проведенных построений.
- Острый угол между диагоналями параллелограмма через площадь
и диагонали - Угол между диагоналями параллелограмма через диагонали и
сторону - Угол между диагоналями параллелограмма через две стороны и
диагонали
Через площадь и диагонали
Для нахождения острого угла между диагоналями параллелограмма следует воспользоваться формулой:
sin α = 2S/(Dd)
где α – острый угол между диагоналями, S – площадь параллелограмма, D и d – его диагонали.
Цифр после
запятой:
Результат в:
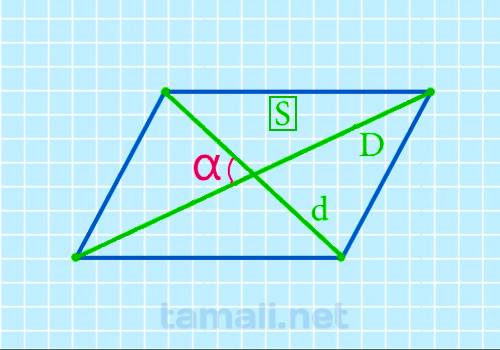
Приведем пример расчета по формуле для наглядного случая, когда диагонали перпендикулярны, и площадь
данного ромба равняется половине площади прямоугольника, в который данный ромб можно вписать.
При D = 20 мм, d = 10 мм, площадь описанного прямоугольника равна 20*10=200 мм², откуда S = 200/2=100 мм².
Вычисления дают sin α = 2S/(Dd) = 2*100/(20*10) = 1, откуда α = 90°. Известный факт – диагонали
ромба перпендикулярны.
Через две стороны и диагонали
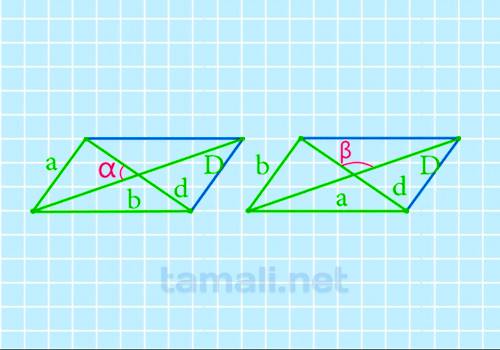
В предыдущей формуле угол определялся через диагонали и одну сторону, в данной задаче требуется
определить угол по диагоналям и 2 сторонам. Тем самым, одно из условий является избыточным, и фигура
по произвольным данным может не оказаться параллелограммом. Но для случая параллелограмма, т.е.
взаимной увязки данных, формулы таковы:
cos α = (b2-a2)/(Dd), cos β = (a2-b2)/(Dd)
где a и b – стороны параллелограмма, α и β – углы между диагоналями (взаимно дополнительные до
180°).
Цифр после
запятой:
Результат в:
Пример приведем по предыдущему случаю, остается только рассчитать недостающую сторону b, которая из
простых соображений (воспользовавшись правилом длины катета против угла в 30°) оказывается равной 20
мм. Вычисляем: cos α = (b²-a²)/(Dd) = (20²-34,64²)/(40*40) = -0,5, откуда
α = 120°.
Через диагонали и сторону
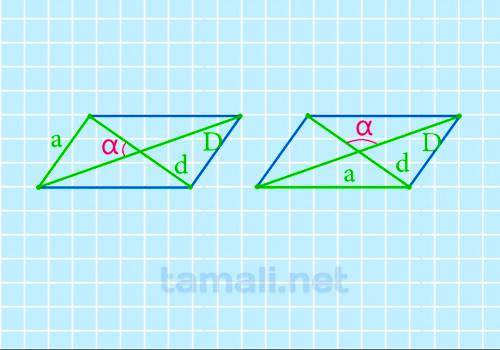
Для нахождения угла между диагоналями параллелограмма через диагонали и сторону формула такова:
cos α = (D² + d² – 4a²)/(2Dd)
где a – сторона параллелограмма, остальные обозначения прежние.
Цифр после
запятой:
Результат в:
Здесь следует считаться с тем, что если в предыдущей задаче угол по условию являлся острым, в данной
задаче он может быть и тупым, с отрицательным значением косинуса угла.
Пример расчета опять-таки по наглядному случаю, когда обе диагонали равны. Это прямоугольник с
диагоналями D = 40 мм и d = 40 мм. При угле между диагоналями 120° половина диагонали составит 40/2 = 20 мм, половина высоты прямоугольника (она же – половина короткой
стороны) составит половину от половины диагонали (в прямоугольном треугольнике противолежащий углу в
30° катет равен половине гипотенузы), т.е. 10 мм, откуда половина стороны параллелограмма составит
√(20²-10²)=√300=17,32 мм, а сторона параллелограмма a = 2*17,32=34,64 мм.
Подставляем в формулу: cos α = (D² + d² – 4a²)/(2Dd) = (40²+40²-4*34,642) = ‑1600/(2*40*40) = -0,5.
Значению косинуса -0,5 соответствует угол 120°. Это же значение даст и калькулятор.
Квадрат достаточно задать одним элементом – стороной. Для задания прямоугольника необходимо задать
уже две его смежные стороны; для ромба сторону и угол между сторонами. Для задания же
параллелограмма необходимо задание 3 его взаимно независимых элементов. Это могут быть 2 смежные
стороны и угол между ними, но возможно и иное задание.
В любом четырехугольнике можно провести 2 диагонали, и они также могут входить в набор элементов для
задания фигуры. В данной статье приводятся справочные формулы для определения угла между диагоналями
параллелограмма через другие его элементы. Рассчитать же этот угол для каждого из 3 рассматриваемых
случаев позволят калькуляторы сайта, в которые необходимо ввести известные элементы, и в результате
получить синус или косинус искомого угла либо сам угол в градусах или радианах.



Найти углы параллелограмма зная длину сторон и диагональ
Введите стороны параллелограмма (a,b) и диагональ (d).
Формула расчёта углов параллелограмма зная длину сторон и диагональ:
cos(α)=(a2+b2-d2)/(2*a*b), β=(360-α*2)/2.
Косинус α равен, сторона (a) в квадрате, плюс сторона (b), в квадрате, и минус диагональ (d), в квадрате. Разделённое на сторону (a), умноженное на сторону (b) и умноженное на два. Угол β – вычитаем из 360 градусов угол α умноженный на два, всё это делим на два.
| Сторона параллелограмма (a) | ||
| Сторона параллелограмма (b) | ||
| Диагональ параллелограмма (d) |
Площадь параллелограмма
Периметр параллелограмма
Найти длину стороны параллелограмма зная диагональ и сторону
Вычислить высоту параллелограмма зная длину стороны и угол
Найти диагональ параллелограмма зная стороны и угол
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
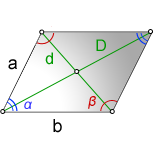
Зная диагонали и сторону a в параллелограмме, можно найти угол пересечения диагоналей, находящийся напротив известной стороны. В треугольнике, образованном половинами диагоналей и стороной параллелограмма, косинус угла будет равен сумме квадратов половин диагоналей за вычетом квадрата стороны a, деленной на удвоенное произведение половин диагоналей.(рис.106.3)
cosγ=(〖d_1/4〗^2+〖d_2/4〗^2-a^2)/((d_1 d_2)/4)=(〖d_1〗^2+〖d_2〗^2-4a^2)/(2d_1 d_2 )
Второй центральный угол является дополнительным до 180 градусов для угла γ, и может быть найден через разность. Затем методом, обратным вышеописанному, из другого треугольника можно найти сторону b.
δ=180°-γ
cosδ=-cosγ
b=√(〖d_1/4〗^2+〖d_2/4〗^2+2d_1 d_2 cosγ )
Зная диагонали и стороны параллелограмма, можно найти углы параллелограмма также через теорему косинусов. (рис.106.2)
cosα=(a^2+b^2-〖d_2〗^2)/2ab
β=180°-α
Высота параллелограмма может быть рассчитана из прямоугольного треугольника, так как, являясь катетом, она относится к гипотенузе, как синус противолежащего ей угла α, вне зависимости от того, на какую сторону она опущена. Поэтому, выразив высоту через синус, можно подставить выражение для стороны a и найти ее через диагонали. (рис.106.1)
h_b=a sinα
h_a=b sinα
Биссектрисой параллелограмма называется отрезок, делящий пополам угол α или β, и проведенный до ближайшей стороны. Примечательно, что для обеих биссектрис отрезок всегда будет пересекать более длинную сторону параллелограмма, образуя равнобедренный треугольник. В таком треугольнике, зная угол и меньшую сторону параллелограмма, можно найти биссектрису, через диагонали это возможно сделать, заменив выражения в формуле эквивалентными. (рис.106.4)
l_α=√(2a^2-2a^2 cosβ )=a√(2-2 cosβ )
l_β= b√(2-2 cosα )
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 05 ноября 2011
-
Обновлено: 13 августа 2021
Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.