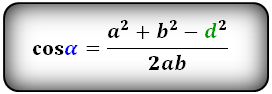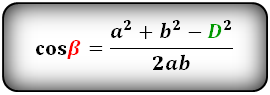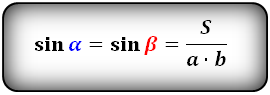У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.
- Острый угол параллелограмма через боковую сторону и
высоту - Острый угол параллелограмма через высоту, сторону и
периметр - Острый угол параллелограмма через площадь и две стороны
- Острый угол параллелограмма через две стороны и короткую
диагональ - Тупой угол параллелограмма через две стороны и длинную
диагональ
Острый угол параллелограмма через боковую сторону и высоту
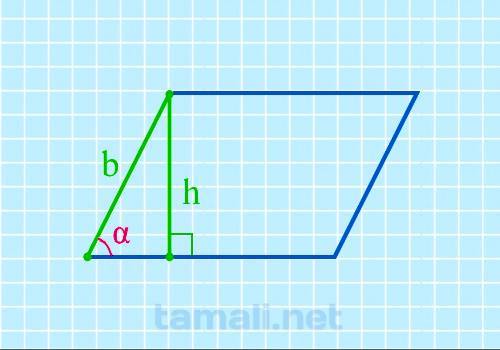
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:
sin α = h / b
где α – острый угол, h – высота, b – боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.
Острый угол параллелограмма через площадь и две стороны
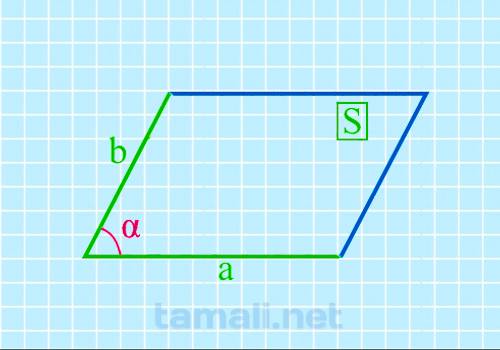
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:
sin α= S / ab
где α – острый угол, S — площадь параллелограмма, a и b – его стороны.
Цифр после
запятой:
Результат в:
Пример. Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.
Острый угол параллелограмма через высоту, сторону и периметр
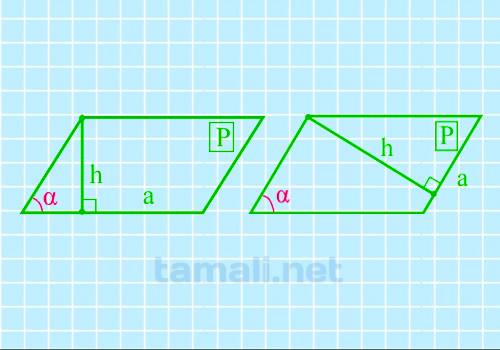
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:
sin α = (2h + a) / P
где α – острый угол, h — высота, a — сторона, P — периметр.
Цифр после
запятой:
Результат в:
Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.
Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.
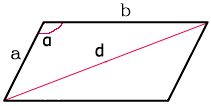
Острый угол параллелограмма через две стороны и короткую диагональ
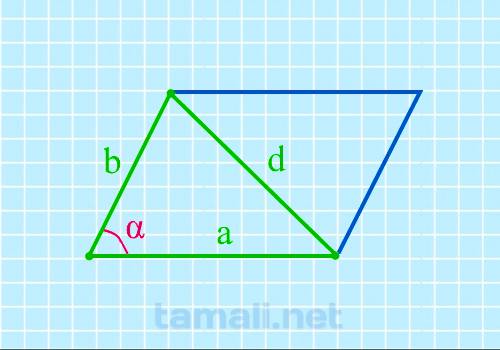
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:
cos α = (a² + b² — d²) / 2ab
где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.
Цифр после
запятой:
Результат в:
Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.
Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.
Тупой угол параллелограмма через две стороны и длинную диагональ
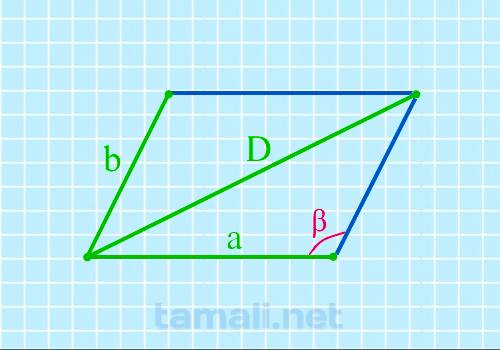
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:
cos β = (a² + b² — D²) / 2ab
где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.
Цифр после
запятой:
Результат в:
Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.
Свойства параллелограмма
У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.
Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.
Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.
Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.
Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.
1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.
Теперь применим это знание для решения задач из ОГЭ.
Задача №1
Для решения, воспользуемся свойством односторонних углов.
Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119
Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.
Точно также решается задача №2 с трапецией.
Меньший угол – это острый угол. Значит 180-131=49
Задача №3
Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.
Найдем меньший угол параллелограмма – он острый, равен 180-105=75
2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Для этой теоремы подходят следующие задачи:
Задача №4
Решение:
Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66
Задача №5
Решение:
Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.
Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80
В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.
Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.



Найти углы параллелограмма зная длину сторон и диагональ
Введите стороны параллелограмма (a,b) и диагональ (d).
Формула расчёта углов параллелограмма зная длину сторон и диагональ:
cos(α)=(a2+b2-d2)/(2*a*b), β=(360-α*2)/2.
Косинус α равен, сторона (a) в квадрате, плюс сторона (b), в квадрате, и минус диагональ (d), в квадрате. Разделённое на сторону (a), умноженное на сторону (b) и умноженное на два. Угол β – вычитаем из 360 градусов угол α умноженный на два, всё это делим на два.
| Сторона параллелограмма (a) | ||
| Сторона параллелограмма (b) | ||
| Диагональ параллелограмма (d) |
Площадь параллелограмма
Периметр параллелограмма
Найти длину стороны параллелограмма зная диагональ и сторону
Вычислить высоту параллелограмма зная длину стороны и угол
Найти диагональ параллелограмма зная стороны и угол
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
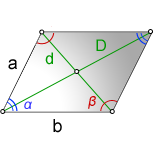
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 05 ноября 2011
-
Обновлено: 13 августа 2021
Углы параллелограмма
Угол
Параллелограмм представляет собой четырехугольник, противоположные стороны которого параллельны и равны друг другу. Два угла, прилежащие к одной стороне параллелограмма, в сумме составляют 180°. Если известен один угол параллелограмма, несложно найти смежный с ним угол путем вычитания из 180° величину известного угла.
α = 180°-β
Таким образом, мы нашли значения всех углов, т.к. известно, что противолежащие углы параллелограмма равны.
Отрезок, проведенный из двух противоположных вершин параллелограмма, является его диагональю. Если заданы стороны и диагональ, можно определить углы параллелограмма. Диагональ делит параллелограмм на два одинаковых треугольника. Основанием треугольника является диагональ, боковыми сторонами — смежные стороны параллелограмма. Для определения угла используем теорему косинусов, по которой квадрат стороны треугольника (в нашем треугольнике это диагональ) равен сумме квадратов двух его сторон, образующих искомый угол, плюс удвоенное произведение этих сторон на косинус угла. Отсюда, косинус искомого угла равен сумме квадратов смежных сторон (а, b) минус квадрат третей стороны треугольника (в нашем случае — диагонали), противолежащей искомому углу, и все это деленное на удвоенное произведение смежных сторон:
d2 = a2 + b2 + 2ab cos (α)
cos (α) = (a2 + b2 — d2) / 2ab
,
где а, b — стороны параллелограмма, d — диагональ.
Воспользовавшись таблицей косинусов находим величину искомого угла. После чего находим смежный с ним угол.