Как найти угол пересечения высот в треугольнике

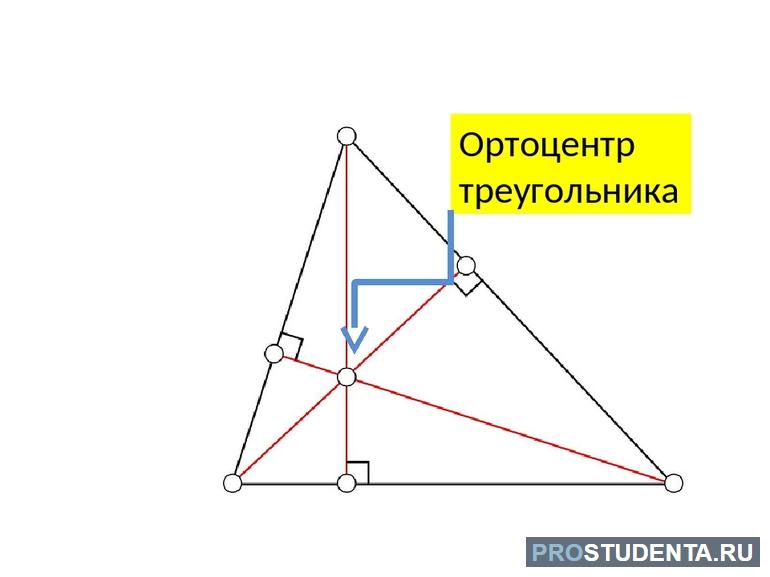
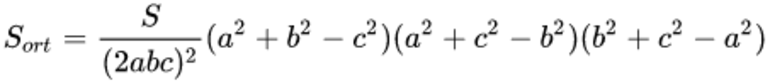Свойства высот треугольника. Ортоцентр

Анна Малкова

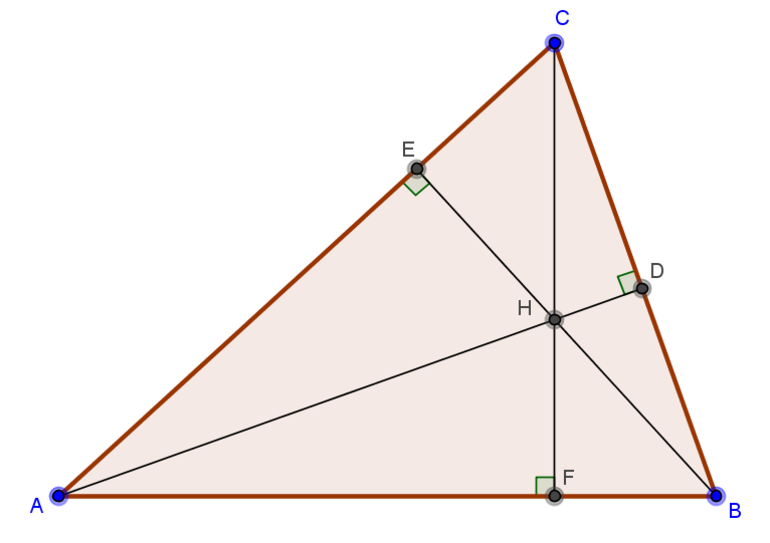
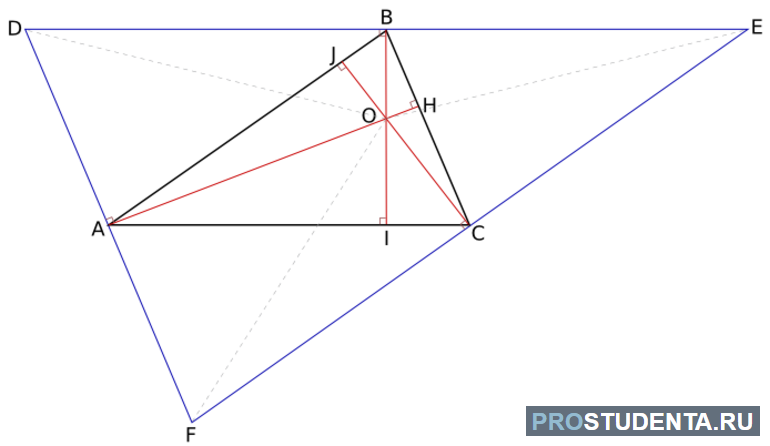
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если 

1. Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
2. Четырехугольник ВКМН также можно вписать в окружность.
3. Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
4. ,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН – прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

– смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

б) Найдем , если и


По теореме синусов,

Свойства высот треугольника

свойства высоты в треугольнике

Свойство 1

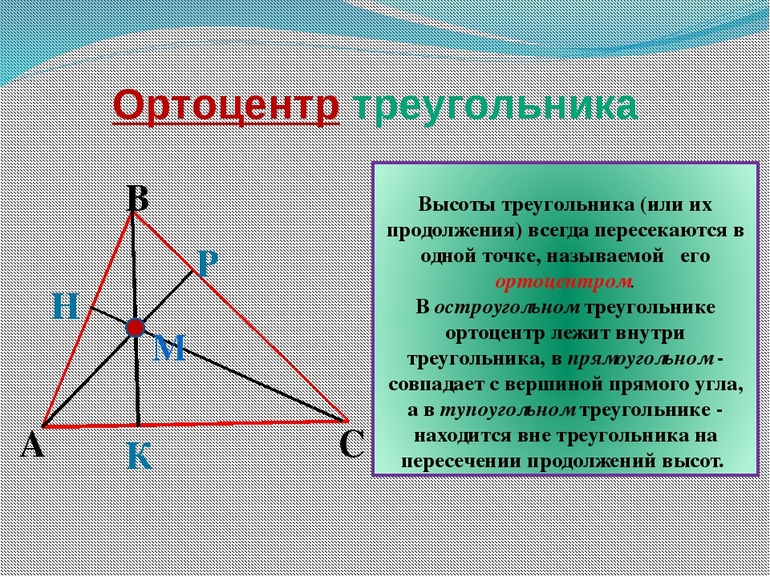
Высоты треугольника или их продолжения пересекаются в одной точке – ортоцентре треугольника.

Свойство 2

Если AD, BE, CF – высоты треугольника ABC, O – точка пересечения этих высот или их продолжений, то:

Свойство 3

Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника, подобных между собой и подобных исходному треугольнику:

Высота на сторону c вычисляется по формулам:

Точка пересечения высот треугольника – свойства, координаты и расположение ортоцентра

Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

• внутри;
• снаружи;
• в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

• H — ортоцентр в ABC;
• О — центр описанной окружности.

Тогда:

• окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
• отрезок BH вдвое длиннее отрезка АС;
• середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Свойства высот треугольника. Ортоцентр

Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если , и , если

1. Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
2. Четырехугольник ВКМН также можно вписать в окружность.
3. Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.
4. ,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН – прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

– смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

[spoiler title=”источники:”]

http://nauka.club/matematika/geometriya/ortotsentr.html

http://ege-study.ru/materialy-ege/svojstva-vysot-treugolnika-ortocentr/

[/spoiler]

Ортоцентр – это точка пересечения высот треугольника.

Рассмотрим остроугольный треугольник ABC:
O – ортоцентр,
∠ BAC = a,
∠ ABC = b,
∠ ACB = c.

Утверждения.
1. Треугольник ABC подобен треугольнику, образованному вершиной B и основанием двух высот:
Δ ABC ∼ Δ H₃BH₂,
коэффициент подобия:
H₃B / AB = H₂B / CB = H₃H₂ / AC = cos b.

2. Соотношение отрезков, на которые ортоцентр делит высоту, можно вычислить по формуле:
BO / OH₁ = cos b / (cos a * cos c).

3. Высоты треугольника можно вычислить по формуле:
BH₁ = AC * sin a * sin c / sin b.

4. Расстояние от ортоцентра до вершины треугольника:
OB = AC / tg b.

5. 1 / BH₁ + 1 / CH₂ + 1 / AH₃ = 1 / r,
r – радиус вписанной окружности.

Докажем эти утверждения.
1.

В треугольнике ABC проведены высоты BD и CE.
Докажем, что треугольник ABC подобен треугольнику ADE.

Решение.
Рассмотрим Δ ABD:
cos A = AD / AB.
Рассмотрим Δ ACE:
cos A = AE / AC.
Таким образом,
cos A = AD / AB = AE / AC.
Значит, Δ ABC ∼ Δ ADE по двум сторонам и углу между ними.

2.

Диагонали трапеции ABCD пересекаются под прямым углом.
CH – высота, проведенная к большему основанию AD.
∠ CAD = a,
∠ ACD = c,
∠ ADC = d.
Найдем отношение, в котором диагональ трапеции делит высоту CH.

Решение.
Пусть K – точка пересечения диагоналей трапеции,
O – точка пересечения диагонали BD и высоты CH. 
Найдем соотношение CO / OH.

Δ BOC подобен Δ DOH по двум углам,
так как ∠ BCO = ∠ DHO = 90,
∠ BOC = ∠ DOH как вертикальные.
Значит,
CO / OH = BC / DH. (*)

Рассмотрим Δ CKD:
KC = CD * cos c.
Рассмотрим Δ BCK:
BC = KC / cos a = (CD * cos c) / cos a.
Рассмотрим Δ CHD:
HD = CD * cos d.

Из (*) и последних трех равенств получаем:
CO / OH = BC / DH =
( (CD * cos c) / cos a ) : (CD * cos d) =

Таким образом, мы нашли соотношение отрезков, на которые ортоцентр O треугольника ABD делит высоту CH:

3.

Найдем расстояние от ортоцентра треугольника до его вершины, и высоту, проведенную из этой вершины, если известны углы треугольника и противолежащая сторона.

Решение.
Рассмотрим треугольник ABC.
O – ортоцентр.
∠ BAC = a,
∠ ABC = b,
∠ ACB = с,
также известна величина стороны AC. 
Найдем BH и OB.

Обозначим AH за x, тогда HC = AC – x.

Рассмотрим Δ AHB:
BH = x * tg a.
Рассмотрим Δ CHB:
BH = (AC – x) * tg c.

Таким образом,
BH = x * tg a = (AC – x) * tg c.

Рассмотрим Δ AHB:

Таким образом высоту можно вычислить по формуле, 

4.
Найдем теперь расстояние от вершины B до ортоцентра.

Так как BH = BO + OH, получаем:

Выражаем из уравнения (1) OH и подставляем в уравнение (2):

Значит, расстояние от ортоцентра до вершины можно вычислить по формуле: 

5.
1 / BH₁ + 1 / CH₂ + 1 / AH₃ = 1 / r.

Площадь треугольника ABC можно вычислить по формуле:
S = ½ * AC * BH₁ = ½ * AB * CH₂ = ½ * BC * AH₃,

Значит,
BH₁ = 2S / AC
CH₂ = 2S / AB
AH₃ = 2S / BC

1 / BH₁ = AC / 2S
1 / CH₂ = AB / 2S
1 / AH₃ = BC / 2S

1 / BH₁ + 1 / CH₂ + 1 / AH₃ = (AC + BC + AB) / 2S = p / S, (*)
где p – полупериметр.

Еще одна формула площади треугольника:
S = p * r,

откуда r = S / p
1 / r = p / S.

Из (*) и последнего равенства получаем нужное нам равенство.

Содержание 👉

Решение задач по геометрии часто сводится к самой простой фигуре, называемой треугольником, точка пересечения высот которого обладает важными свойствами, помогающими найти неизвестные величины: стороны, углы, периметр и площадь. В интернете можно найти немало информации по этой теме, но, как правило, она не систематизирована. В результате тратится много времени на поиск формул и важных утверждений.

Оглавление:

• Общие сведения
• Информация об ортоцентре
• Полезные свойства и формулы

Общие сведения

Перед переходом к основным соотношениям высот с другими параметрами треугольника нужно ознакомиться с теоретическими сведениями об этой фигуре. Треугольник — фигура, состоящая из трех вершин, не лежащих на одной прямой, и отрезков, соединяющих их. Упрощенная форма записи в математике — символ «тильда», т. е. Δ. После последнего идут названия трех вершин, например, ΔPTS. Угол обозначается символом ∠, а после него указывается полная запись (∠РТS) или сокращенная (∠a).

Специалисты рекомендуют не называть вершины русскими буквами, поскольку эта запись не является верной. Треугольники бывают нескольких типов, на основании которых можно применить некоторые свойства, утверждения (теоремы) и формулы.

Типы треугольников

Математики классифицируют треугольные фигуры по определенным правилам или критериям. Они отличаются между собой по сторонам и углам. В первом случае фигуры бывают:

• произвольными;
• равнобедренными;
• равносторонними.

К первым принадлежат все фигуры с различными сторонами, ко вторым — с двумя равными, а к третьим — с тремя. Если классифицировать Δ по углам, то фигуры можно разделить на три типа. К ним принадлежат:

• прямоугольные;
• тупоугольные;
• остроугольные.

В прямоугольном Δ один из углов является прямым, т. е. равным 90 градусам. Тогда, используя свойство суммы его ∠, можно сделать вывод, что при сложении последних получается величина, равная 90°. Если Δ тупоугольный, то один из его ∠ эквивалентен величине, которая больше 90°. В остроугольном Δ все ∠ имеют градусную меру меньше 90°.

Следует отметить, что произвольные и равнобедренные Δ бывают прямоугольными и тупоугольными. Однако равносторонние (правильные) могут быть только остроугольными, поскольку все их углы эквивалентны значению 60°. Это можно определить по формуле: ∠K = ∠L = ∠M = 180 / 3 = 60. Кроме того, только вокруг этого типа фигуры можно описать окружность.

Основные и дополнительные параметры

У каждой фигуры, а треугольник не является исключением, существуют основные и дополнительные параметры. К первым относятся стороны и углы, ко вторым — периметр, площадь, высота, медиана и биссектриса.

Периметр — совокупность или алгебраическая сумма значений длин всех его сторон. Площадью является размерность фигуры, которая рассчитывается по некоторому соотношению. Она может быть только у плоских элементов геометрии, кроме точки, прямой, угла, луча и отрезка.

Следует отметить, что при решении задач в фигуре проводятся дополнительные элементы: высота, биссектриса и медиана. Первой называется отрезок, который проводится из вершины треугольника на противоположную сторону под углом 90 градусов. Высота образует подобный Δ относительного того, где она проведена. Это утверждение следует из равенства двух углов и пропорциональности сторон.

Все высоты в остроугольном треугольнике расположены внутри него. Если Δ является прямоугольным, то высоты, которые проводятся из вершин его острых углов, совпадают с катетами. В тупоугольном Δ высота, проведенная из вершины любого острого ∠, всегда находится вне фигуры.

Следующим вспомогательным отрезком является медиана. Она проводится из вершины, как и высота, но не под прямым углом, а соединяет среднюю точку противоположной стороны, посредством которой и будет делиться на две равные части. Биссектриса делит угол на две равные части. Она проводится из вершины Δ.

В произвольном Δ количество высот, медиан и биссектрис эквивалентно числу его вершин, то есть можно провести по три элемента. Однако бывают исключения из этого правила: если фигура равнобедренная или равносторонняя, то ее высота является медианой и биссектрисой.

Информация об ортоцентре

Теорема об ортоцентре позволяет вывести важные свойства высот треугольника, пересекающихся в одной точке. Ее формулировка следующая: высоты, проведенные в произвольном Δ, пересекаются в одной точке. Для доказательства требуется начертить произвольный ΔKLM. Он не должен содержать прямой или тупой угол. Далее нужно действовать по такому алгоритму:

1. Из двух вершин следует провести высоты, которые пересекают противоположную сторону под прямым углом, то есть из вершины L опустить LN на сторону КМ. Аналогичную операцию нужно выполнить для вершины К (KU к LM).
2. Высоты пересекутся в некоторой точке — будущем ортоцентре треугольника. Ее следует обозначить W.
3. Предположим, что высоты не пересекаются. Следовательно, они параллельны. Это записывается таким образом: LN || KU. Сторона KL является секущей по определению.
4. Исходя из третьего пункта, алгебраическая сумма значений углов (∠К/2 и ∠L/2) эквивалентна 180. Из равенства получается, что ∠К + ∠L = 360. Если ∠К и ∠L — внутренние углы ΔKLM, то их сумма не может составлять 360 градусов. Следовательно, предположение ошибочно.
5. На основании доказанного в четвертом пункте утверждения можно сделать вывод, что высоты пересекаются в точке W.
6. Аналогичным образом доказывается, что высота MV, опущенная из вершины M, проходит через ортоцентр. Для этого нужно повторить 1—5 пункты алгоритма, но вместо KU провести MV.
7. Утверждение доказано.

Однако теоремы о высотах недостаточно для решения задач по геометрии. Для этого случая математики вывели полезные свойства и соотношения, облегчающие нахождение неизвестной величины или доказательства нового утверждения.

Полезные свойства и формулы

При решении задач могут потребоваться некоторые свойства ортоцентра, которые были доказаны математиками. К ним относятся следующие:

1. Расположение ортоцентра: остроугольный — в центре, прямоугольный — совпадает с образующей прямой угол вершиной, тупоугольный — внешний (находится за пределами треугольника).
2. Ортоцентр остроугольного Δ — центр окружности, вписанной в него.
3. Алгебраическая сумма квадратов расстояний от вершин до ортоцентра (KW, LW и MW) с учетом квадратов сторон (KL, LM и KM) эквивалентна двенадцати квадратам радиуса окружности R, которая описана вокруг треугольника: KW² + LW² + MW² + KL² + LM² + KM² = 12 * R².
4. Расстояние (К{kl}) от ортоцентра до середины стороны KL: К{kl} = KL / (2 * tg (∠K)). Для других величин (К{lm} и К{mk}): К{lm} = LM / (2 * tg (∠L)) и К{mk} = MK / (2 * tg (∠M)) соответственно.
5. Величина расстояний от W до вершин (KW, LW и MW): KW = KL / tg (∠K), LW = LM / tg (∠L) и MW = KM / tg (∠M).
6. Площадь S: S = KL² * sin (∠K) / 2 = LM² * sin (∠L) / 2 = KM² * sin (∠M) / 2.

Существует определенный класс задач, в которых требуется найти координаты ортоцентра. В этом случае нужно начертить декартовую систему координат и отметить на ней вершины, а затем соединить их отрезками. Далее необходимо провести высоты и найти ортоцентр треугольника, а затем начертить из искомой точки проекции на координатные прямые.

Таким образом, расположение ортоцентра треугольника зависит от его вида и является важным параметром для построения вписанных и описанных окружностей.

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Определение высоты треугольника

Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

Свойства высоты треугольника

Свойство 1

Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

• GE = EL
• GD = DM
• GF = FK

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.