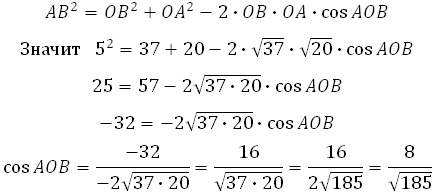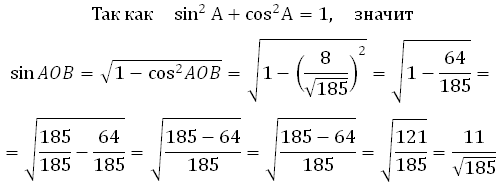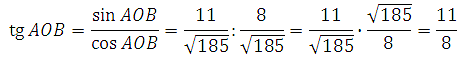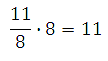Как найти угол по клеткам в градусах - Сайт, где вы сможете решить свои вопросы

Как вычислить градусную меру угла по клеточкам ?

Определить размер угла в градусах по клеточкам можно, выполнив следующие действия:

Нарисовать угол на сетке так, чтобы вершина угла совпадала с точкой пересечения линий сетки.
Из вершины угла рисуется окружность, которая разбивается на дуги точками пересечения с линиями сетки, причем пересечения с горизонтальной и вертикальной линиями вблизи узлов сетки (или в узле) считаются одной точкой.
Надо подсчитать количество получившихся дуг и определить угол соответствующий каждой дуге, если получилось N дуг, то каждой будет соответствовать угол в 360/N градусов (это размер дуги в градусах).
Подсчитать количество дуг, которые расположены внутри угла и умножить на размер дуги градусах.

По клеточкам можно найти косинус или синус угла

без рисования окружности.

Знаете ответ?

На клетчатой бумаге изображён вписанный угол

Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

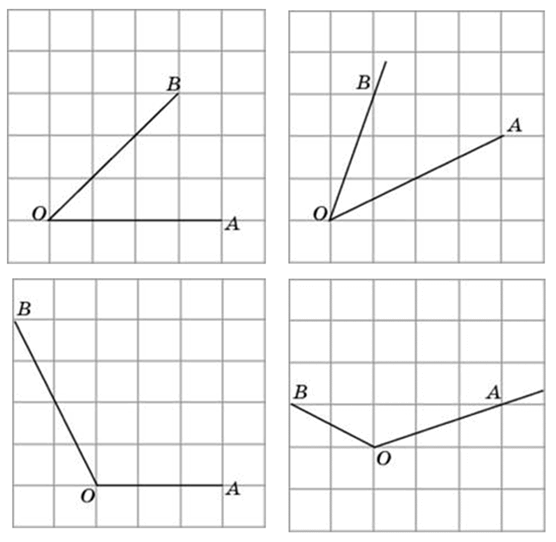
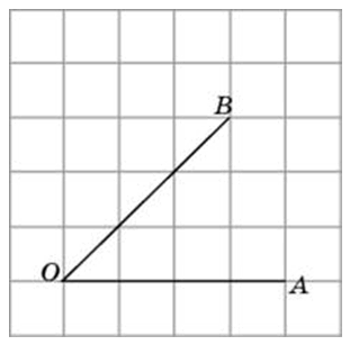
Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.

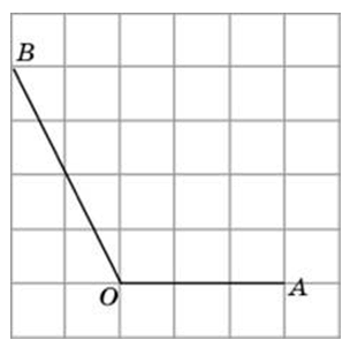
Чему равен этот угол?

Понятно, что 45 градусам.

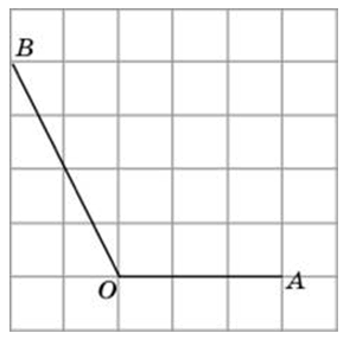
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

225 градусов (180 + 45 или 360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:

По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).

27887. Найдите величину угла ABC . Ответ дайте в градусах.

27888. Найдите величину угла ABC. Ответ дайте в градусах.

27889. Найдите величину угла ABC . Ответ дайте в градусах.

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

Как найти величину угла по клеткам в окружности

На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.

Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.

На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.

Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:

Найдите угол ABC. Ответ дайте в градусах.

Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.

[spoiler title=”источники:”]

Круг на клетчатой бумаге

http://oge.sdamgia.ru/search?search=%D0%9D%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D1%83%D0%B3%D0%BE%D0%BB%20ABC

[/spoiler]

Источник

Построение углов на клетчатом листе без транспортира

Решение задач по геометрии начинается с выполнения чертежа. От того насколько точно он выполнен, зависит исход решения задачи. Особенно коварно себя ведут углы. Зачастую ошибка в 10° при выполнении чертежа и задача может быть решена неправильно. Но как известно, на экзаменах ОГЭ (9 класс) и ЕГЭ (11 класс) по математике использование транспортира не допускается. Но существует универсальный способ построение острых углов без транспортира с шагом в 10°.

Алгоритм их построения угла К числу десятков искомого угла прибавить единицу-это количество клеток по вертикали, которые необходимо отсчитать от вершены угла . Полученный результат отнять от 11- это количество клеток по горизонтали, которые необходимо отсчитать от вершены угла.
Например, для построения угла в 30° нужно отступить от вершины угла 4 (3+1) клетки по вертикали и 7 (11-4) клетки по горизонтали .
Остается только выучить «координаты» для углов 10° и 80° (6;1) и (1;6).

Построение углов на клетчатом листе без транспортира

Делись этой информацией с друзьями!

Источник

Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.

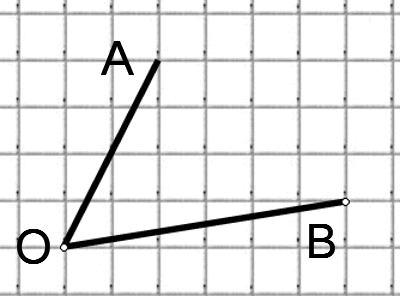
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):

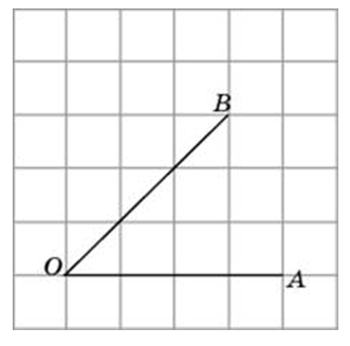
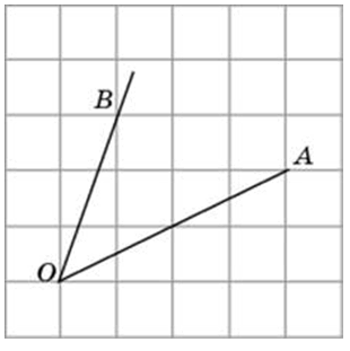
Итак, рассмотрим задание:

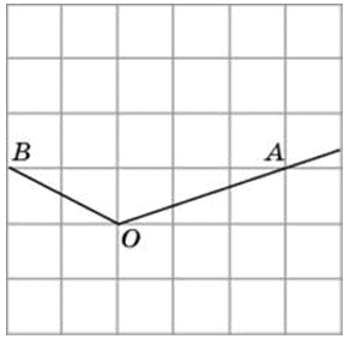
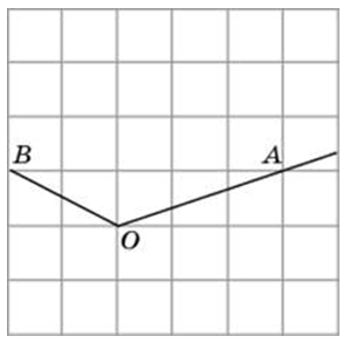
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.

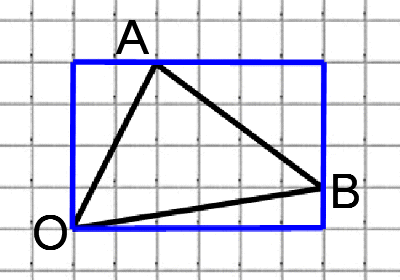
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.

Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).

АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,

ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,

OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,

По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Из основного тригонометрического тождества можем найти sin AOB:

*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.

Теперь можем найти тангенс:

Умножим результат на 8 и запишем ответ:

Ответ: 11

Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.

Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.