Как найти угол по косинусу по формуле - Сайт, где вы сможете решить свои вопросы

Найти угол, зная косинус угла: примеры решения

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.

Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).

Замечание 1

Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.

Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:

Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ

Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.

В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.

Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ

Пример 1

Найдите, чему равен $arccos 0,456$.

Решение:

Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:

Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ

После нажатия кнопки мы получили значение $α = 27,129°$.

Пример 2

Определите, чему равен угол, если известен его косинус, и он равен $0,95$.

Решение:

Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Источник

Страница содержит полную информацию о теореме косинусов, а также калькулятор, с помощью которого можно найти стороны и угол треугольника и формулу теоремы косинусов.

Теорема косинусов обобщает теорему Пифагора на произвольные плоские треугольники и устанавливает соотношение между сторонами треугольника и его углами.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов

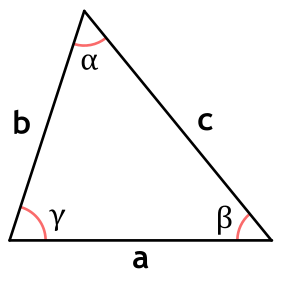
{a^2 = b^2 + c^2-2bc cos (alpha)}
{b^2 = a^2 + c^2-2ac cos (beta)}
{c^2 = a^2 + b^2-2ab cos (gamma)}

a, b, c – стороны треугольника,

α, β, γ – углы треугольника.

Источник

Загрузить PDF

Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ .

1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.^[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — неизвестная сторона, — косинус угла, противоположного неизвестной стороне, и — две известные стороны.^[2]
3
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку . Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.^[4] Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.
- Например, косинус 89° ≈ 0,01745. Итак: $c^{{2}}=5^{{2}}+9^{{2}}-2(5)(9)(0,01745)$ .
5

Перемножьте числа. Умножьте на косинус известного угла.
6

Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
7

Вычтите два числа. Вы найдете $c^{{2}}$ .
8

Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.^[5]

Реклама

1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.^[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — косинус неизвестного угла, — известная сторона, противолежащая неизвестному углу, и — две другие известные стороны. ^[7]
3
4
Перемножьте числа. Умножьте на косинус неизвестного угла.
- Например, $12^{{2}}=8^{{2}}+10^{{2}}-160cos {C}$ .
5
Возведите в квадрат. То есть умножьте число само себя.
- Например, $144=8^{{2}}+10^{{2}}-160cos {C}$
6

Сложите квадраты и . Но сначала возведите соответствующие числа в квадрат.
7

Изолируйте косинус неизвестного угла. Для этого вычтите сумму $a^{{2}}$ и $b^{{2}}$ из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.^[9] На калькуляторе функция арккосинуса обозначается $COS^{{-1}}$ .
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама

1

Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
2

Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
3

Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.

Реклама

Советы

Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.

Об этой статье

Эту страницу просматривали 5394 раза.

Была ли эта статья полезной?

Источник

Как найти угол имея цифровое значение синуса, косинуса, тангенса,котангенса? например есть значение sin a=0,3452 какой угол этому соответствует?

Функции: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), называются тригонометрическими. Они выражают зависимости длин сторон от углов треугольника при гипотенузе. Определяются отношением какой-либо из сторон треугольника к другой. То есть, показывают, насколько одна сторона больше другой. Это отношение может быть характерно только для строго определенного угла. Выражаются тригонометрические функции в безразмерных единицах.

Если известно значение какой-либо тригонометрической функции (в данном случае, синуса – sin), а требуется найти соответствующий ему угол в градусах, то нужно:

найти обратную тригонометрическую функцию, так называемую “arc”: arcsin, arccos, arctg, arcctg.. Эти функции находятся: по таблицам Брадиса, в которых для каждого угла приведены свои – строго определенные значения тригонометрических функций (таблицами Брадиса пользовались в “докомпьютерный век”), с помощью “инженерных” калькуляторов или компьютерными программами, в частности – Excel. Для того, чтобы определить значение угла по таблицам Брадиса, нужно водить пальцем по их строкам (с тысячами значений), где найти нужную величину (то ли 5, то ли 6 знаков после запятой). И увидеть соответствующее ему значение угла. Так что, с помощью Excel это делается несравненно быстрее и точнее.
Однако функции arc показывают значение в радианах. Искомый угол равен 0,35245 радиан. Если нужно в градусах, то следуют применить еще и формулу перевода радиан в градусы.

asin

Определение значения arcsin угла (в радианах) и значения в градусах – с помощью функций Excel

Итак, ответ получен:

Синусу угла альфа со значением 0,3452 соответствует угол 20,194 градуса.

автор вопроса выбрал этот ответ лучшим

RIOLIt
[176K]

6 лет назад

Данному значению синуса соответствует угол- немногим более 20 градусов, это- по таблице, а если есть значение гипотенузы, то- по отношению- можно найти катет и другие элементы треугольника и- возможно- все улы, здесь- главное- зацепка- кончик ниточки, чтобы размотать весь клубочек,( а имея в

хозяйстве инженерный калькулятор, можно сразу- по функции найти угол с точностью до н- ого знака после запятой…)

Можно без компьютера, без калькулятора, без таблиц Брадиса найти этот угол. Для этого нужен такой инструмент, как транспортир. Можно воспользоваться угломером. Если есть чертежный прибор, который еще называют кульман, то и им. Но сначала высисляют катет и гипотенузу. Чем больше длина, тем точгее. Допустим, гипотенуза 100 мм, тогда противолежащий катет будет равен 100*0,3452=34,52мм. Берем клетчатую бумагу, по вертикали откладываем 35 мм от горизонтальной линии вверх. Из верхней точки циркулем с разведенными ножками на 100 мм делаем засечку на глризонтальной линии. Соединяем три точки линиями и измеряем угол.

Если честно, то в повседневной жизни не припомню, чтобы приходилось определять углы по синусу или тагенсу. Вот строить углы приходится постоянно. Например, нужно обрезать плинтуса под углом 45 градусов. Никакой транспортир или угломер не нужен. На заводе плинтус обрезан под прямым углом, тогда просто отмеряешь два одинаковых катета и проводишь гипотенузу, угол получантся сам собой. Так же легко строить углы 30 и 60 градусов, так как гипотенуза равна двум противолежащим катетам.

Еще углы можно измерять смартфоном илитпланшетом, если в нем установлено приложение по измерению углов, очень удобная штука, не надо покупать строительный уровень.

bezdelnik
[34.1K]

6 лет назад

Найти угол имея цифровое значение синуса, косинуса, тангенса можно по таблицам Брадиса, на логарифмической линейке или на калькуляторе. Если sin a=0,3452, то a=20,194… градуса. Можно найти приближенное значение тригонометрических функций по их графикам, для синуса и косинуса это графики синусоиды и косинусоиды. Найдя значения синуса и косинуса значения тангенса и котангенса можно вычислить по формулам tg a = Sin a /Cos a, ctg a = Cos a/Sin a

DartFallen
[68.2K]

6 лет назад

Я открою Вам одну старую и великую тайну! Все эти величины давно вычислены и сведены в таблицу. Носит она название таблицы Браддиса.

Когда я учился в старших классах у каждого ученика была желтенькая такая брошюрка, в которой и представлены многие данные и не только для градусной меры углов. Величины эти постоянные и периодического пересчета не требуют.

Вот как-то так…

Blockphild
[0]

8 месяцев назад

Зачем так все сложно и это в век компьютеров? Иди сюда -> https://allcalc.ru/node/1039

вставляй величины катетов и гипотенуз –> жми на кнопку -> ВЫЧИСЛИТЬ и вот тебе результат в градусах и радианах.

Недостаток: нужно иметь интернет

Не надо никаких там EXCEL, таблиц Брадисов и прочей ерунды, мы в 21 веке живем, все делается очень быстро.

Успехов!

bezdelnik
[34.1K]

5 лет назад

Для некоторых значений тригонометрических функций соответствующие углы общеизвестны из учебников по математике. Например,для углов 0°, 30°, 45°, 60°, 90° синус равен 0, 1/2, √2/2, √3/2, 1 ,соответственно, а косинус такие же значения в обратном порядке. Это должны знать все получившие среднее школьное образование.

Знаете ответ?

Смотрите также:

В треугольнике АВС угол С равен 90°, АВ=10, АС=√51. Как найти sin A?

Как вычислить площадь параллелограма по формуле S=a·b·sin A с след.данными?

В треугольнике ABC угол C = 90°, sin A = 4/5, AC=9. Найти AB. Как решить?

Как доказать теорему о равенстве синусов острых углов?

Как построить угол, если известен синус?

Если синус X равен 1, чему равен косинус X(см)?

Как найти котангенс, тангенс, синус, косинус?

Как выучить таблицу значений синуса, косинуса, тангенса разных углов?

Перечислите все формулы, объединяющие синус, косинус, тангенс и котангенс?

Как записать две различные функции для синуса и косинуса?

Источник

Стандартные обозначения углов и сторон треугольника

Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.

Формулировка[править | править код]

Для плоского треугольника со сторонами a,b,c и углом alpha , противолежащим стороне ,
справедливо соотношение:

${displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha .}$

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними^[1]

Доказательства[править | править код]

Классическое доказательство

Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:

откуда

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

$h^{2}=b^{2}-(bcos alpha )^{2}qquad qquad qquad (1)$

$h^{2}=a^{2}-(c-bcos alpha )^{2}qquad qquad (2)$

Приравниваем правые части уравнений (1) и (2) и:

$b^{2}-(bcos alpha )^{2}=a^{2}-(c-bcos alpha )^{2}$

или

$a^{2}=b^{2}+c^{2}-2bccos alpha$

Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.

Выражения для сторон b и c:

$b^{2}=a^{2}+c^{2}-2accos beta$

$c^{2}=a^{2}+b^{2}-2abcos gamma$

Доказательство через координаты

Одним из доказательств является доказательство её в координатной плоскости.

Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c, AC=b, CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα).
Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
$a^{2}=(bcos {a}-c)^{2}+b^{2}sin ^{2}{a}$
$a^{2}=b^{2}cos ^{2}{a}-2bccos {a}+c^{2}+b^{2}sin ^{2}{a}$
$a^{2}=b^{2}(cos ^{2}{a}+sin ^{2}{a})+c^{2}-2bccos {a}$
Так как
$cos ^{2}{a}+sin ^{2}{a}=1$ (основное тригонометрическое тождество), то
$a^{2}=b^{2}+c^{2}-2bccos {a}$
Теорема доказана.
Для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² – известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.

Доказательство через векторы

Ниже подразумеваются операции над векторами, а не длинами отрезков
${displaystyle AC=AB+BC=>BC=AC-AB=>BC^{2}=AC^{2}+AB^{2}-2cdot ACcdot AB}$

Так как скалярное произведение векторов равно произведению их модулей (длин) на косинус угла между ними, последнее выражение можно переписать:
${displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha }$
где a, b, c — длины соответствующих векторов

Следствия[править | править код]

Теорема косинусов может быть использована для нахождения косинуса угла треугольника

$cos {alpha }={frac {b^{2}+c^{2}-a^{2}}{2bc}}$

В частности,

Теорема косинусов может быть записана также в следующем виде^[2]:

$a^{2}=(b+c)^{2}-4cdot bcdot ccdot cos ^{2}(alpha /2)$

$a^{2}=(b-c)^{2}+4cdot bcdot ccdot sin ^{2}(alpha /2)$

Доказательство

Последние две формулы мгновенно следуют из основной формулы теоремы косинусов (см. в рамке выше), если в правой её части воспользоваться формулами разложения квадрата суммы (для второй формулы – квадрата разности) двух членов на квадратный трехчлен, являющийся полным квадратом. Для получения окончательного результата (двух формул выше) в правой части надо еще воспользоваться известными тригонометрическими формулами:

$1+cos alpha =2cdot cos ^{2}(alpha /2)$

$1-cos alpha =2cdot sin ^{2}(alpha /2)$

Кстати, вторая формула формально не содержит косинусов, но её все равно именуют теоремой косинусов.

Для других углов[править | править код]

Теорема косинусов для двух других углов имеет вид:

${displaystyle c^{2} =a^{2}+b^{2}-2abcos gamma }$

${displaystyle b^{2} =a^{2}+c^{2}-2accos beta }$

Из этих и из основной формулы могут быть выражены углы:

${displaystyle alpha =arccos left({frac {b^{2}+c^{2}-a^{2}}{2bc}}right)}$

${displaystyle beta =arccos left({frac {a^{2}+c^{2}-b^{2}}{2ac}}right)}$

${displaystyle gamma =arccos left({frac {a^{2}+b^{2}-c^{2}}{2ab}}right)}$

История[править | править код]

Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.

Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.^[3]^:105
Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.

В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии.
В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.

Вариации и обобщения[править | править код]

Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
Теоремы косинусов (геометрия Лобачевского)
Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):

$AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}.$

Для евклидовых нормированных пространств[править | править код]

Пусть в евклидовом пространстве задана норма, ассоциированная со скалярным произведением, то есть . Тогда теорема косинусов формулируется следующим образом:

Теорема.
$leftVert {vec {a}}-{vec {b}}rightVert ^{2}=leftVert {vec {a}}rightVert ^{2}+leftVert {vec {b}}rightVert ^{2}-2({vec {a}},{vec {b}})$

Для четырёхугольников[править | править код]

Возводя в квадрат тождество можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников:

$d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B-2accos omega -2bccos angle C$

, где

— угол между прямыми AB и CD.

Или иначе:

$d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B+2accos(angle A+angle D)-2bccos angle C$

Формула справедлива и для тетраэдра, под

подразумевается угол между скрещивающимися ребрами.

С помощью неё можно найти косинус угла между скрещивающимися ребрами

зная все ребра тетраэдра:

${displaystyle cos w=(b^{2}+d^{2}-e^{2}-f^{2})/2ac}$

Где

пары скрещивающихся ребер тетраэдра.

Косвенный аналог для четырёхугольника[править | править код]

Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:

Между сторонами a, b, c, d и противоположными углами и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:

${displaystyle e^{2}f^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos(alpha +gamma )}$

Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.

Симплексы[править | править код]

${displaystyle S_{i}S_{j}cos angle A={frac {(-1)^{(n-1+i+j)}}{2^{n-1}((n-1)!)^{2}}}{begin{vmatrix}0&1&1&1&dots &1\1&0&d_{12}^{2}&d_{13}^{2}&dots &d_{1(n+1)}^{2}\1&d_{21}^{2}&0&d_{23}^{2}&dots &d_{2(n+1)}^{2}\1&d_{31}^{2}&d_{32}^{2}&0&dots &d_{3(n+1)}^{2}\vdots &vdots &vdots &vdots &ddots &vdots \1&d_{(n+1)1}^{2}&d_{(n+1)2}^{2}&d_{(n+1)3}^{2}&dots &0\end{vmatrix}}}$

при этом мы должны зачеркнуть строку и столбец, где находится $d_{ij}$ или $d_{ji}$ .

A — угол между гранями $S_{i}$ и $S_{j}$ , $S_{i}$ -грань, находящаяся против вершины i, $d_{ij}$ – расстояние между вершинами i и j.

См. также[править | править код]

Решение треугольников
Скалярное произведение
Соотношение Бретшнайдера
Теорема косинусов для трёхгранного угла
Теорема о проекциях
Теорема Пифагора
Сферическая теорема косинусов
Теорема котангенсов
Теорема синусов
Теорема тангенсов
Тригонометрические тождества
Тригонометрические функции

Примечания[править | править код]

↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
↑ ¹ ² Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
↑ Florian Cajori. A History of Mathematics — 5th edition 1991

Литература[править | править код]

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.

Источник

Найти угол, зная косинус угла: примеры решения

Формула теоремы косинусов

Советы

Об этой статье

Была ли эта статья полезной?

Формулировка[править | править код]

Доказательства[править | править код]

Следствия[править | править код]

Для других углов[править | править код]

История[править | править код]

Вариации и обобщения[править | править код]

Для евклидовых нормированных пространств[править | править код]

Для четырёхугольников[править | править код]

Косвенный аналог для четырёхугольника[править | править код]

Симплексы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Тимвьювер пишет коммерческое использование как исправить

Как найти общую напряженность в точке

Как составить свое резюме в word

Добавить комментарий Отменить ответ