Найти угол, зная косинус угла: примеры решения
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).
Замечание 1
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите, чему равен $arccos 0,456$.
Решение:
Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
После нажатия кнопки мы получили значение $α = 27,129°$.
Пример 2
Определите, чему равен угол, если известен его косинус, и он равен $0,95$.
Решение:
Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Синус, косинус, тангенс и котангенс
Острые углы в прямоугольном треугольнике.
В геометрии определения синуса, косинуса, тангенса и котангенса мы изучаем на примере острых углов в прямоугольном треугольнике.
Вот и они:

Возьмем прямоугольный треугольник АВС и распишем для него формулы для нахождения синуса, косинуса, тангенса и котангенса острых углов α и β.
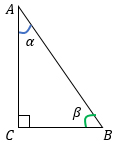
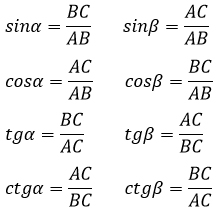
Острые углы прямоугольного треугольника обладают очень интересными сверхспособностями, которые могут пригодится при решении геометрических задач.
Во-первых, их сумма равна 90°.
Во-вторых, верны будут следующие равенства (доказать их верность очень легко – смотри предыдущие 8 формул):
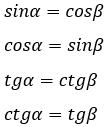
Смежные углы.
Теперь немного отстранимся от прямоугольных треугольников. Есть еще очень клевые формулы, но они подходят для смежных углов.
Пусть даны смежные углы α и β (напомню, что сумма смежных углов равна 180°).
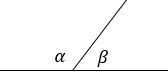
Для них будут верны следующие равенства (доказываются через формулы приведения, т.к. α = 180° – β):
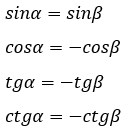
Формулы приведения.
| Функции | Углы | ||||||||
| -α | 90°-α | 90°+α | 180°-α | 180°+α | 270°-α | 270°+α | 360°-α | 360°+α | |
| sin | -sinα | +cosα | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα |
| cos | +cosα | +sinα | -sinα | -cosα | -cosα | -sinα | +sinα | +cosα | +cosα |
| tg | -tgα | +ctgα | -ctgα | -tgα | +tgα | +ctgα | -ctgα | -tgα | +tgα |
| ctg | -ctgα | +tgα | -tgα | -ctgα | +ctgα | +tgα | -tgα | -ctgα | +ctgα |
Таблица значений тригонометрических функций для “прекрасных” углов.
| α | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| tgα | 0 | √3/3 | 1 | √3 | – | 0 | – | 0 |
| ctgα | – | √3 | 1 | √3/3 | 0 | – | 0 | – |
Осталось это всё запомнить и научиться применять на практике)
Вообще, достаточно запомнить информацию только про синусы и косинусы, а уже через них выводить значения тангенса и котангенса.
Еще рекомендую к прочтению статью про тригонометрические тождества.
Успехов в подготовке!
С уважением, Васильева Анна.
Угол между векторами.

Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Сложение векторов: длина суммы векторов и теорема косинусов
Определения скалярного произведения векторов через угол между ними
Сложение векторов по правилу треугольника (суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора приложено к концу вектора ) даёт возможность упрощать выражение перед вычислением произведений векторов.
Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке “Векторы и операции над векторами”.
Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С – не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия – одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.
При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть и – векторы, – угол между ними, а – сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:
,
где – угол, смежный с углом . У смежных углов одна сторона общая, а другие стороны лежат на одной прямой (см. рисунок выше).
Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:
.
В случае вычитания векторов () происходит сложение вектора с вектором , противоположным вектору , то есть имеющим ту же длину, но противоположным по направлению. Углы между и и и между и являются смежными углами, у них, как уже было отмечено, одна сторона общая, а другие стороны лежат на одной прямой. В случае вычитания векторов для нахождения длины разности векторов нужно знать следующее свойство косинусов смежных углов:
косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.
Перейдём к примерам.
Сложение векторов – решение примеров
Пример 1. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .
Решение. Из элементарной тригонометрии известно, что .
Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус “изначального” угла:
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 2. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .
Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:
Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус “изначального” угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус “изначального” угла:
Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус “изначального” угла (задача обратная по отношению к примеру 1) и находим его:
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :
Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Пример 5. Векторы и взаимно перпендикулярны, а их длины . Найти длину их суммы и и длину их разности .
Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол – тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения – произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:
Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:
1) длина суммы векторов равна длине разности векторов, т. е. ,
2) длина суммы векторов больше длины разности векторов, т. е. ,
3) длина суммы векторов меньше длины разности векторов, т. е. ?
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/
http://function-x.ru/vectors_cosinus.html
[/spoiler]
Смежные углы. Свойства смежных углов
Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.
На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:
Свойства смежных углов
1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.
Справедливость пунктов 2 и 3 очевидны и следуют из (1).
Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)
То есть синусы смежных углов равны.
Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но
То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Определение арккосинуса(arccos)
Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
Функция арккосинус не является четной или нечетной
Видео
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.
Теорема косинусов
Для любого треугольника справедливо равенство:
a2 = b2 + c2 — 2b × c × cosA,
где угол A — это угол, противолежащий стороне a.
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
a2 = b2 + c2,
где a — гипотенуза.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6. Из треугольника АВС найдем cos B:

- Из треугольника СМВ по теореме косинусов найдём СМ:



Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:

- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.

- Если c2 < a2 + b2, то ∠C — острый.




