Хорда равна радиусу
Если хорда равна радиусу окружности, то какие из этого можно сделать выводы?
Если хорда равна радиусу окружности, то она стягивает дугу 60º.
Дано : окружность (O; R)
Рассмотрим треугольник AOB.
OA=OB=R, хорда AB по условию также равна радиусу: AB=R, следовательно, AB=OA=OB, то есть треугольник AOB — равносторонний.
Величина дуги равна величине опирающегося на неё центрального угла, то есть хорда AKB стягивает дугу в 60º:
(Кроме того, поскольку градусная мера окружности равна 360º, а 60º — одна шестая часть от 360º, то дуга AKB составляет шестую часть окружности).
Что и требовалось доказать .
Так как вписанный угол равен половине соответствующему ему центрального угла (либо равен половине дуги, на которую он опирается), то
- центральный угол, опирающийся на хорду, равную радиусу, равен 60º;
- вписанный угол, опирающийся на хорду, равную радиусу, равен 30º.
Вычисление углов в окружности
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ вычисление величин углов в окружности .doc
Задания для самостоятельной работыдома по-образцу. Учащихся перед началов классной работы следует предупредить о необходимости сравнивать решенную в классе задачу и с той, которую предстоит решать самому.
Центральный угол на 51 о больше вписанного угла, опирающегося на ту же дугу. Найдите вписанный угол.
Под каким углом из точки C дуги окружности видна стягивающая ее хорда, если дуга содержит 100 о ?
Под каким углом из точки дуги окружности видна стягивающая ее хорда, если дуга составляет одну треть окружности?
Угол ACB , величиной 50 о , вписан в окружность. Найдите градусную величину дуги ACB .
На рисунке угол ACB равен 30 о , угол AEF равен 40 о . Найдите угол BDF .
На рисунке угол A равен 40 о , угол B равен 30 о , угол D равен 45 о . Найдите угол EFC .
Острый вписанный угол опирается на хорду, которая делит окружность на две части, градусные величины которых относятся как 4 : 5. Найдите этот угол.
Точки А, В, С, расположенные на окружности, делят эту окружность на три дуги, градусные величины которых относятся как 2 : 3 : 7. Найдите больший угол треугольника АВС.
Окружность разделена точками A , B , C , D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите меньший угол четырехугольника ABCD .
Окружность разделена точками A , B , C , D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите угол между диагоналями AC и BD четырехугольника ABCD .
Задания для тех, кто изучает математику на расширенном уровне.
Выбранный для просмотра документ вычисление величин углов в окружности.ppt
Описание презентации по отдельным слайдам:
Углы, связанные с окружностью
Угол с вершиной в центре окружности называется центральным.
Каждый центральный угол данной окружности определяют дугу окружности, которая состоит из точек окружности, принадлежащих этому углу.
Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным.
Углы, связанные с окружностью
Вписанный угол измеряется половиной дуги окружности.
Вписанный угол
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности.
Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
Углы, связанные с окружностью
Угол между касательной и хордой
Угол, с вершиной на окружности, одна сторона которого лежит на касательной, а вторая – пересекает окружность, измеряется половиной дуги окружности, лежащей внутри этого угла.
Угол с вершиной внутри окружности
Теорема. Угол, с вершиной внутри окружности, измеряется полусуммой дуг, на которые опираются данный угол и вертикальный с ним угол.
Угол с вершиной вне окружности
Теорема. Угол, с вершиной вне окружности, стороны которого пересекают окружность, измеряется полуразностью дуг окружности, заключенных внутри этого угла.
Угол с вершиной вне окружности
Теорема. Угол, с вершиной вне окружности, одна сторона которого лежит на касательной к окружности, а вторая сторона пересекает окружность, измеряется полуразностью дуг окружности, заключенных внутри этого угла.
Угол с вершиной вне окружности
Теорема. Угол, с вершиной вне окружности, стороны которого лежат на касательных к окружности, измеряется полуразностью дуг окружности, заключенных внутри этого угла.
Упражнение 1
Чему равен вписанный угол, опирающийся на диаметр окружности?
Ответ: 90о.
Упражнение 2
Найдите центральный угол AOB, опирающийся на хорду AB, равную радиусу.
Ответ: 60о.
Упражнение 3
Угол ACB вписан в окружность. Градусные величины дуг AC и BC равны 98о и 48о соответственно. Найдите угол ACB.
Ответ: 107о.
Упражнение 4
Ответ: 30о.
Найдите вписанный угол, опирающийся на дугу, которая составляет окружности.
Упражнение 5
Ответ: 18о.
Найдите вписанный угол, опирающийся на дугу, которая составляет 10 % окружности.
Упражнение 6
Вписанный угол на 35 меньше центрального угла, опирающегося на ту же дугу. Найдите вписанный угол.
Ответ: 35о.
Упражнение 11
Ответ: 50о.
Вершины треугольника ABC, вписанного в окружность, делят окружность на части, градусные величины которых равны 100о, 120о и 140о. Найдите наименьший угол треугольника ABC.
Упражнение 12
Ответ: 45о.
Сторона AB треугольника ABC равна , радиус описанной окружности равен 1. Найдите угол C.
Упражнение 13
Ответ: 30о.
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне.
Упражнение 15
Углы ABC и BCD вписаны в окружность и равны 45о и 30о соответственно, S – точка пересечения AD и BC. Найдите угол ASC.
Ответ: 75о.
Упражнение 16
Хорда CD пересекает диаметр AB окружности под углом 60о. Градусная величина дуги AD равна 80о. Найдите градусную величину дуги BC.
Ответ: 40о.
Упражнение 18
Стороны угла с вершиной C вне окружности отсекают от окружности дуги A1B1, A2B2, градусные величины которых равны 30о и 100о. Найдите угол C.
Ответ: 35о.
Упражнение 19
Углы ABC и BCD вписаны в окружность и равны 20о и 50о соответственно, S – точка пересечения прямых AB и CD. Найдите угол ASC.
Ответ: 30о.
Упражнение 20
Стороны угла с вершиной C вне окружности отсекают от окружности дуги AB1, AB2, градусные величины которых равны 60о и 140о соответственно, CA – касательная. Найдите угол C.
Ответ: 40о.
Упражнение 21
Через концы дуги в 60о проведены касательные, пересекающиеся в точке C. Найдите угол ACB.
Ответ: 120о.
Упражнение 22
Хорда АВ стягивает дугу окружности в 44о. Найдите углы, которые образует эта хорда с касательными к окружности, проведенными через ее концы.
Ответ: 22о.
Упражнение 23
Две равные окружности расположены таким образом, что каждая из них проходит через центр другой. Найдите угол, под которым видна их общая хорда AB из центра O1 одной из окружностей.
Ответ: 120о.
Упражнение 25
Ответ: 90о.
Точки А, В, С, расположенные на окружности c с центром в точке O, делят эту окружность на три дуги, градусные величины которых относятся как 3 : 4 : 5. Найдите угол AOB.
Упражнение 28
В четырехугольнике ABCD, вписанном в окружность, угол A равен 75о, угол B равен 90о. Найдите разность двух других углов.
Ответ: 15о.
Упражнение 29
Углы A и C вписанного в окружность пятиугольника ABCDE равны 120о и 100о соответственно. Найдите угол DBE.
Ответ: 40о.
Упражнение 30
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите угол между диагоналями AC и BD четырехугольника ABCD.
Ответ: 80о.
Упражнение 7
Центральный угол на 51о больше вписанного угла, опирающегося на ту же дугу. Найдите вписанный угол.
Ответ: 51о.
Упражнение 8
Под каким углом из точки C дуги окружности видна стягивающая ее хорда, если дуга содержит 100о?
Ответ: 130о.
Упражнение 9
Под каким углом из точки дуги окружности видна стягивающая ее хорда, если дуга составляет одну треть окружности?
Ответ: 120о.
Упражнение 10
Угол ACB, величиной 50о, вписан в окружность. Найдите градусную величину дуги ACB.
Ответ: 260о.
Упражнение 14
На рисунке угол ACB равен 30о, угол AEF равен 40о. Найдите угол BDF.
Ответ: 70о.
Упражнение 17
На рисунке угол A равен 40о, угол B равен 30о, угол D равен 45о. Найдите угол EFC.
Ответ: 115о.
Упражнение 24
Острый вписанный угол опирается на хорду, которая делит окружность на две части, градусные величины которых относятся как 4 : 5. Найдите этот угол.
Ответ: 80о.
Упражнение 26
Ответ: 105о.
Точки А, В, С, расположенные на окружности, делят эту окружность на три дуги, градусные величины которых относятся как 2 : 3 : 7. Найдите больший угол треугольника АВС.
Упражнение 27
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите меньший угол четырехугольника ABCD.
Ответ: 60о.
Задания 31-42 предназначены для самостоятельной работы
учеников, желающих развивать математические навыки.
Упражнение 31
На рисунке угол A равен 120о, угол C равен 110о. Найдите угол E.
Ответ: 130о.
Упражнение 32
Хорда CD перпендикулярна радиусу OB окружности и пересекает его в середине E. Найдите градусную величину дуги BC.
Ответ: 60о.
Упражнение 33
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 1:2:3:4. Найдите угол между прямыми AD и BC.
Ответ: 36о.
Упражнение 34
Из точки вне окружности проведены к ней две касательные. Кратчайшее расстояние от этой точки до окружности равно радиусу окружности. Найдите угол между касательными.
Ответ: 60о.
Упражнение 35
В угол АСB вписана окружность. Точки касания делят окружность на дуги, градусные величины которых относятся как 3:2. Найдите величину угла АCB.
Ответ: 36о.
Упражнение 36
В угол АСB, величиной 50о, вписана окружность. Точки касания делят окружность на две дуги. Найдите градусную величину наибольшей дуги окружности, заключенной внутри угла ACB.
Ответ: 230о.
Упражнение 37
В угол АСB, величиной 45о, вписана окружность. Точки касания делят окружность на две дуги. Найдите число, выражающее отношение градусных величин меньшей и большей дуг окружности, заключенных внутри угла ACB.
Ответ: 3:5.
Упражнение 38
Окружность разделена точками А, В, С на дуги, градусные величины которых относятся как 11 : 3 : 4. Через точки А, В, С проведены касательные до их взаимного пересечения. Найдите наибольший угол образовавшегося треугольника DEF.
Ответ: 80о.
Упражнение 39
Треугольник ABC вписан в окружность. Угол A равен 40о, угол B равен 60о. Найдите угол между касательной к окружности, проведенной через вершину C и прямой AB.
Ответ: 20о.
Упражнение 40
Треугольник ABC вписан в окружность. Угол A равен 40о, угол B равен 60о. Найдите угол между касательными к окружности, проведенной через вершины A и B.
Ответ: 20о.
Упражнение 41
Стороны четырехугольника ABCD касаются окружности в точках, делящих эту окружность на четыре части, градусные величины которых относятся как 8:7:11:10. Найдите наименьший угол четырехугольника ABCD.
Ответ: 70о.
Упражнение 42
Две окружности касаются внешним образом в точке C, AB – их общая внешняя касательная, A и B – точки касания. Найдите угол ACB.
Ответ: 90о.
Выбранный для просмотра документ рабочий лист окружность.doc
Рабочий лист темы «Окружность».
Окружность—это множество точек плоскости, находящихся на одном расстоянии от точки, являющейся центром окружности . П.21
Хорда—это отрезок, соединяющий две точки окружности. П.21 Свойство отрезков хорд.
Круг—это множество точек плоскости, ограниченной окружностью.
S = R 2
=
Радиус—это отрезок, соединяющий центр и точку на окружности.
R = C / 2
= 3, 14….
Длина окружности — это длина дуги, соответствующая
центральному углу в 360. П.114
C = 360 градусов
Длина окружности —это длина отрезка, соответствующего окружности, вытянутой в прямую линию. П.114
C = 2 R ( см) = 2 * 3,14* R
C = 2 R
Диаметр—это хорда, проходящая через центр.
Касательная — это прямая, которая имеет с окружностью только одну общую точку . П.71 Свойства касательной :
1. Радиус, проведенный в точку касания, перпендикулярен касательной. Нарисуй 1
2. П.74 Центр окружности лежит на биссектрисе угла, образованного двумя касательными, проведенными из одной точки к окружности. Нарисуй 2
3. П.74 Отрезки двух касательных, проведенных из одной точки к окружности, равны.
1. Нарисуй свойство 1
2. Нарисуй свойство 2
3. Нарисуй свойство 3
Свойство секущей и касательной. *
Нарисуй свойства и определения
Центральный угол образован радиусами, выходящими из центра.
Вписанный угол образован двумя хордами, выходящими из одной точки.
Вписанный угол, опирающийся на диаметр
Вписанные углы, опирающиеся на одну и ту же дугу.
угол между секущей и касательной.
угол между касательными.
Он равен дуге, на которую опирается.
Его величина равна половине дуги, на которую он опирается.
Вписанный угол, опирающийся на диаметр прямой
Вписанные углы, опирающиеся на одну и ту же дугу, равны
Дуга окружности – это часть окружности, заключенной между радиусами.
Длина дуги L =
Сектор—это часть круга, ограниченного радиусами и дугой . П.115
Площадь круга S = *
Краткое описание документа:
В данном материале предложены: презентация, содержащая теоретический и практический материал по теме “Углы в окружности”. С помощью ее можно решить около 50 задач темы.Рабочий лист, содержащий материал темы, который можно использовать для изучения и повторения материала. А также как опорную схему для решения задач;Лист с чертежами к задачам презентации и набор задач для самостоятельного решения по- образцу задачи, решенной в классе.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 988 человек из 78 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 310 человек из 68 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 673 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 538 748 материалов в базе
Материал подходит для УМК
«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
§ 2. Центральные и вписанные углы
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 06.02.2022
- 13
- 0
- 06.02.2022
- 22
- 0
- 06.02.2022
- 20
- 0
- 06.02.2022
- 24
- 0
- 06.02.2022
- 16
- 0
- 06.02.2022
- 20
- 0
- 06.02.2022
- 19
- 0
- 06.02.2022
- 18
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 06.02.2022 13
- RAR 1.2 мбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Воробьева Галина Васильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала

- На сайте: 6 лет и 7 месяцев
- Подписчики: 0
- Всего просмотров: 40604
- Всего материалов: 55
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России классы будут переводить на дистант, если заболели 20% детей
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Минпросвещения определило порядок получения заключений на международные договоры
Время чтения: 1 минута
Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d9621a2cc2f7b1b • Your IP : 85.95.188.35 • Performance & security by Cloudflare
[spoiler title=”источники:”]
http://infourok.ru/vychislenie-uglov-v-okruzhnosti-5749585.html
http://mathvox.ru/geometria/okrujnosti-i-ih-svoistva/glava-9-hordi-i-sekuschie/esli-horda-ravna-radiusu/
[/spoiler]
04
Ноя 2021
Категория: 01 Геометрия
2021-11-04
2022-09-11
Задача 1. Найдите хорду, на которую опирается угол вписанный в окружность радиуса
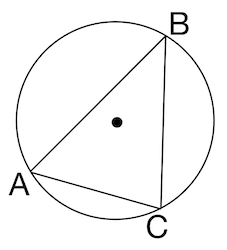
Решение: + показать
Задача 2. Найдите хорду, на которую опирается угол вписанный в окружность радиуса

Решение: + показать
Задача 3. Хорда делит окружность на две части, градусные величины которых относятся как
Под каким углом видна эта хорда из точки
, принадлежащей большей дуге окружности? Ответ дайте в градусах.

Решение: + показать
Задача 4. Хорда стягивает дугу окружности в
Найдите угол
между этой хордой и касательной к окружности, проведенной через точку
Ответ дайте в градусах.

Решение: + показать
Задача 5. Через концы и
дуги окружности с центром
проведены касательные
и
Угол
равен
Найдите угол
. Ответ дайте в градусах.

Решение: + показать
Задача 6. Касательные и
к окружности образуют угол
равный
Найдите величину меньшей дуги
стягиваемой точками касания. Ответ дайте в градусах.

Решение: + показать
Задача 7. Через концы
дуги окружности в
проведены касательные
и
Найдите угол
Ответ дайте в градусах.

Решение: + показать
Задача 8. Найдите угол если его сторона
касается окружности,
— центр окружности, а меньшая дуга окружности
заключенная внутри этого угла, равна
Ответ дайте в градусах.

Решение: + показать
Задача 9. Угол равен
где
— центр окружности. Его сторона
касается окружности. Найдите величину меньшей дуги
окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение: + показать
Задача 10. Угол равен
. Его сторона
касается окружности. Найдите градусную величину дуги
окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение: + показать

Вы может пройти тест
Автор: egeMax |
Нет комментариев
Как найти угол по хорде и радиусу? Если знаете — ответьте
Как найти угол, под которым видна хорда известной длины из центра окружности? Радиус известен
Угол, под которым хорда видна из центра, образован двумя радиусами. Так что система «два радиуса и хорда» образует равнобедренный треугольник, для которого хорда — основание. Почему равнобедренный — думаю, понятно.
А теперь опустим из центра перпендикуляр на эту хорду. Раз треугольник равнобедренный, то это будет и высота, и медиана, и биссектриса того самого угла, который мы хотим найти. Ну и вполне очевидно, что половинаНу и как только нашли половину угла, не штука найти и весь угол.
Рубрика — образование
Волкова Е.А.
Профи
(730),
закрыт
12 лет назад
На которую хорда делит окружность?
злато-серебро
Оракул
(87912)
12 лет назад
Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. В данном случае эта хорда видна из любой точки большей дуги под углом. равным половине угла 140 градусов, то-есть 70°.
Из любого точки мéньшей дуги угол, под которым видна эта хорда, равен 110°.
Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Спрятать решение
Решение.
Из точки C хорда АВ видна под углом АCВ. Пусть большая часть окружности равна 7x, тогда меньшая равна 5x.
Значит, меньшая дуга окружности равна 150°, а большая — 210°. Вписанный угол равен половине дуги, на которую он опирается, значит, опирающийся на большую дугу угол АCВ равен 105°.
Ответ: 105.
Кодификатор ФИПИ/Решу ЕГЭ:
