Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
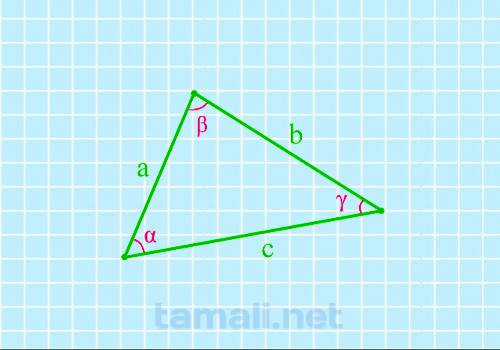
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
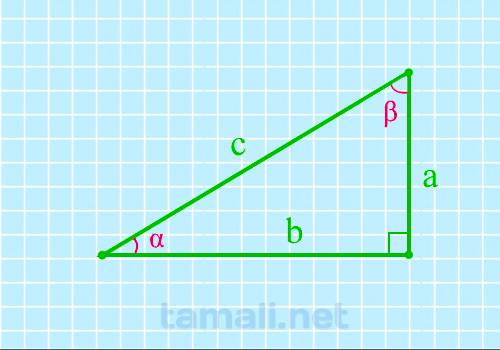
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
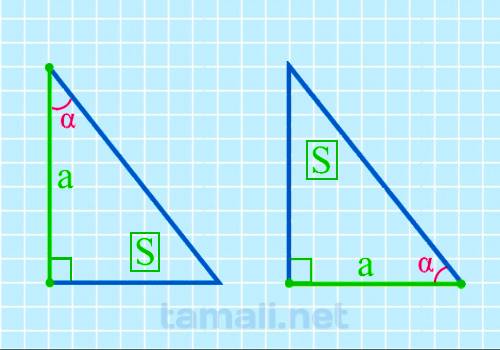
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
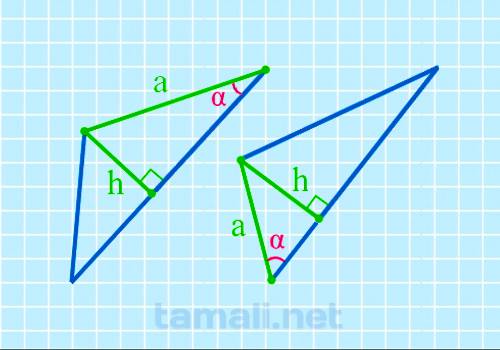
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
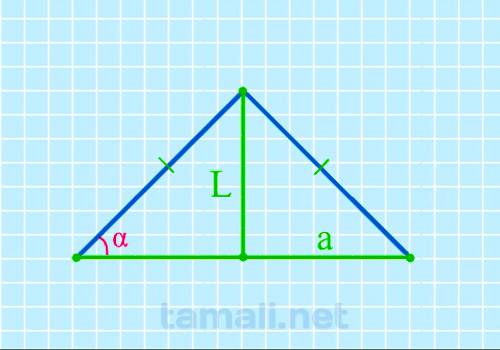
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
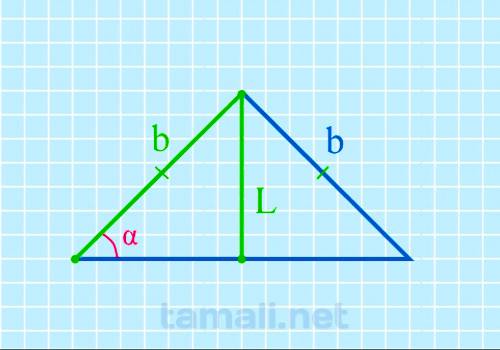
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
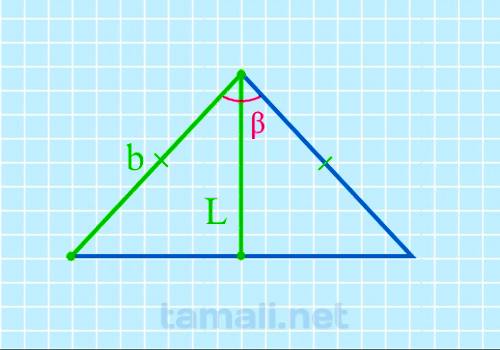
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
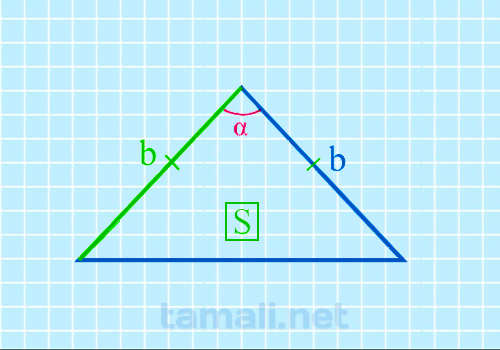
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
Лучший ответ
Бенцион Гопник
Оракул
(57326)
13 лет назад
есть разные инженерные калькуляторы и везде по разному. . Ну обычно над кнопкой cos наверху написано cos -1 -имеется ввиду арккосинус. Так вот надо нажать на кнопку которая переключает с того что написано на кнопках на то, что написано над кнопками. обычно 2-ndf -вторичная функция. и потом нажать на косинус
Остальные ответы
Николай Михалевич
Знаток
(298)
13 лет назад
арккосинус тебе в помощь
иван пастухов
Ученик
(214)
13 лет назад
зависит от калькулятора)
иногда есть арки, иногда нет
если нет, то подбором)
Yupi
Мыслитель
(9607)
13 лет назад
набираешь известное число и жмешь кнопку архкосинус
alfer
Мастер
(1338)
13 лет назад
написать число, поставить галку на inv и жать на коминус
Как найти углы прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти углы прямоугольного треугольника
Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Если ∠β = , то ∠α =
0
Если ∠α = , то ∠β =
0
Формула
α = 90° – β
β = 90° – α
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
или так:
α = arctg(a/b)
β = arctg(b/a)
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°
∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
∠α =
0
∠β =
0
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Формулы
sin(α) = a/c
sin(β) = b/c
cos(α) = b/c
cos(β) = a/c
или так:
α = arcsin(a/c) = arccos(b/c)
β = arcsin(b/c) = arccos(a/c)
Пример
Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:
∠α = arccos(3/6) = arccos(0.5) = 60°
∠β = arcsin(3/6) = arcsin(0.5) = 30°
См. также
Информация по назначению калькулятора
Треугольник – это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.
В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.
Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:
⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° – это правильный многоугольник.
⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник – это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.
⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.
Треугольники также могут быть классифицированы в соответствии с их внутренними углами:
⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны – катеты треугольника.
⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).
⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник – это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.
⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.
Онлайн калькулятор поможет найти параметры треугольника, такие как:
- Длины сторон
- Углы
- Высота
- Периметр
- Площадь
- Медианы
- Биссектрисы
- Радиус Вписанной и Описанной окружностей
- Диаметр Вписанной и Описанной окружностей
- Длина Вписанной и Описанной окружностей
- Площадь Вписанной и Описанной окружностей
– равны в равностороннем треугольнике
– также равны в равностороннем треугольнике
– это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
– равен сумме всех 3х сторон (P=AB+BC+AC)
– равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)
Содержание
- Как найти косинус на калькуляторе
- Нахождение косинусного соотношения
- Использование коэффициента косинуса для определения угла
- подсказки
- Как найти угол, используя синус, тангенс и косинус
- Как найти котангенс на графическом калькуляторе
- Как построить график и найти решение на калькуляторе
- Найти угол, зная косинус угла: примеры решения
- Таблица косинусов, найти значения угла косинусов
- Таблица косинусов от 0° — 360°
Как найти косинус на калькуляторе
Использование косинуса в калькуляторе экономит много времени по сравнению с поиском в таблице, что люди делали до калькулятора. Косинус происходит от части математики, называемой тригонометрия, которая имеет дело с отношениями между сторонами и углами в прямоугольных треугольниках. Косинус определенно имеет дело с отношением между одним из непрямых углов, его смежной стороной и гипотенузой.
Нахождение косинусного соотношения
Проверьте режим калькулятора. На научных калькуляторах это отображается на экране. Для построения графиков калькуляторов нажмите «Режим». Если вы используете градусы (как правило, если вы находитесь в геометрии), калькулятор должен быть установлен в градусах или «градус». Если вы используете радианы (предкалькуляция или тригонометрия), для него следует установить радианы или «радианы».
Нажмите кнопку «Cos», расположенную в центре калькулятора. «Cos» — это сокращение от косинуса. Ваш калькулятор должен отображать «cos (.»
Введите меру угла, для которого вы хотите узнать коэффициент косинуса. Например, 45 градусов.
Закройте скобки, нажав «).»
Нажмите клавишу ввода. Калькулятор должен отображать ваш коэффициент косинуса в десятичном виде. В этом примере вы должны увидеть 0, 7071.
Использование коэффициента косинуса для определения угла
Проверьте режим калькулятора. На научных калькуляторах это отображается на экране. Для построения графиков калькуляторов нажмите «Режим». Если вы используете градусы (как правило, если вы находитесь в геометрии), калькулятор должен быть установлен в градусах или «градус». Если вы используете радианы (предкалькуляция или тригонометрия), для него следует установить радианы или «радианы».
Нажмите кнопку «2nd», а затем нажмите «Cos». Ваш калькулятор должен отображать «cos» с отрицательным 1 для показателя степени и открытых скобок.
Введите коэффициент косинуса. Это длина соседней стороны, деленная на длину гипотенузы. Например, используйте 1/2. Нажмите клавишу «1», клавишу деления, а затем клавишу «2».
Нажмите Ввод.» Калькулятор покажет угол для вашего косинуса. В этом примере калькулятор должен отображать 60 градусов.
подсказки
При вводе угла он не должен быть больше 90 градусов, поскольку углы не соответствуют теореме о треугольной сумме углов. При вводе коэффициента косинуса у вас никогда не должно быть неправильной доли, потому что гипотенуза будет больше по определению и находится в знаменателе.
Как найти угол, используя синус, тангенс и косинус

Функции синуса, косинуса и тангенса часто должны использоваться для решения угловых задач в алгебраических, геометрических и тригонометрических тестах. Как правило, одному дается длина двух сторон прямоугольного треугольника и предлагается найти меру одного или всех углов в треугольнике. Расчет угла требует, чтобы вы использовали либо .
Как найти котангенс на графическом калькуляторе

В тригонометрии котангенс является обратной величиной касательной. Формула для определения касательной — это противоположная сторона, разделенная на соседнюю сторону треугольника. Итак, поскольку котангенс является обратным, то формулой для определения котангенса является смежная сторона, разделенная на противоположную сторону .
Как построить график и найти решение на калькуляторе

Графические калькуляторы — это один из способов помочь студентам понять взаимосвязь между графиками и решением ряда уравнений. Ключом к пониманию этой взаимосвязи является знание того, что решение уравнений является точкой пересечения графиков отдельных уравнений. Нахождение точки пересечения .
Источник
Найти угол, зная косинус угла: примеры решения
![]()
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
С нами работают 108 689 преподавателей из 185 областей знаний. Мы публикуем только качественные материалы
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^<-1>$, а $cos$ на $cos^<-1>$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^<-1>$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Найдите, чему равен $arccos 0,456$.
Решение:
Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^<-1>$ обведена красным:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
После нажатия кнопки мы получили значение $α = 27,129°$.
Определите, чему равен угол, если известен его косинус, и он равен $0,95$.
Решение:
Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.
- Telegram
- Вконтакте
- Одноклассники
![]()
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
С нами работают 108 689 преподавателей из 185 областей знаний. Мы публикуем только качественные материалы
Эксперты на Автор24 помогут сделать любую учебную работу!
Эксперты на Автор24 помогут сделать любую учебную работу!
Источник
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
Таблица косинусов от 0° — 360°
|
|
|
|
|
|
|
|
|
|
Пожалуйста напишите с чем связна такая низкая оценка:
Источник
