Исходим из уравнения
![]() (1)
(1)
И покажем, что всегда можно выбрать угол поворота ![]() координатных осей так, что “смешанный” член
координатных осей так, что “смешанный” член ![]() обратится в нуль. Пусть система координат X”O’y” получена поворотом системы X’O’y’ вокруг начала O’ на угол
обратится в нуль. Пусть система координат X”O’y” получена поворотом системы X’O’y’ вокруг начала O’ на угол ![]() .
.
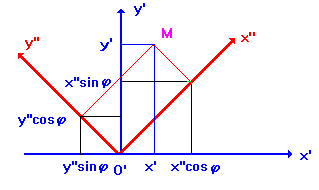
Как видно из рисунка, “старые” и “новые” координаты связаны равенствами
![]() (2)
(2)
Подставим их в уравнение (1)
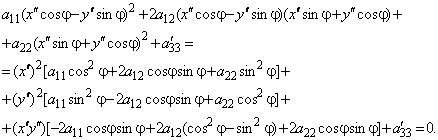 Последнюю квадратную скобку перепишем в виде
Последнюю квадратную скобку перепишем в виде ![]() и выберем угол j так, чтобы она обращалась в нуль:
и выберем угол j так, чтобы она обращалась в нуль:
![]() .
.
Разделим это уравнение на ![]() , получим
, получим ![]() . Откуда найдем искомый угол
. Откуда найдем искомый угол
![]() . (3)
. (3)
Обозначая в (2) первые квадратные скобки ![]() , а вторые
, а вторые ![]() , получим уравнение (20.4) в “новой” системе координат
, получим уравнение (20.4) в “новой” системе координат
![]() . (4)
. (4)
ВЫВОД: Для кривой, заданной уравнением (1), поворотом осей координат можно “уничтожить” смешанный (билинейный) член и преобразовать его к уравнению (4); при этом свободный член не изменяется.
Пример 1. Поворотом осей координат установить тип кривой, заданной уравнением
![]() .
.
Сравнивая с уравнением (20.4), находим
![]() .
.
По формуле (3) найдем угол поворота ![]() .
.
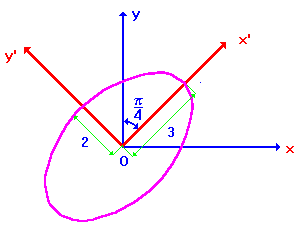
Итак, для приведения кривой к каноническому виду следует сделать поворот осей на угол ![]() , при этом формулы перехода даются (2):
, при этом формулы перехода даются (2):
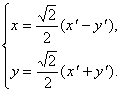
Подставим эти значения в исходное уравнение, получим
![]() .
.
Разделим уравнение на свободный член и перенесем его в правую часть уравнения, получим ![]() – это эллипс с полуосями
– это эллипс с полуосями ![]() .
.
| < Предыдущая | Следующая > |
|---|
Приведение кривой второго порядка к каноническому виду
Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:
Характеристическое уравнение:
; λ1=-2, λ2=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x1 2 -2y1 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x1=1: x 1=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x 1.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x 2=(1,1); .
Итак, имеем новый ортонормированный базис ( i 1, j 1).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или
Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 – 20 = 0.
Решение.Пример 2
Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение
Задание. Привести уравнение к каноническому виду: 16x 2 – 9y 2 -64x – 8y +199 = 0.
Решение.Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение
Преобразования декартовой системы координат с примерами решения
Содержание:
Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат
Пример:
Дана точка М(3;2) и начало новой системы координат Вычислить положение точки М в новой системе отсчета.
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол (Рис. 47):
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода
Найдем обратное преобразование системы координат, найдем матрицу обратную к матрице А:
Найдем алгебраические дополнения всех элементов
Запишем обратную матрицу
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол
Решение:
Воспользуемся полученными формулами т.е. в новой системе координат точка имеет координаты М(2; -1).
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы
Пример:
Преобразовать уравнение параболы к каноническому виду.
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка – начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда
следовательно, параметр параболы р = 1/4.
б) Выяснить, какую кривую описывает функция
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение
и новые координаты получим уравнение которое описывает равнобочную гиперболу.
Полярные координаты. Замечательные кривые
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).
Рис. 48. Полярная система координат.
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами
Рассмотрим замечательные кривые в полярной системе координат:
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.
Рис. 49. Спираль (улитка) Архимеда.
2. Уравнение окружности: уравнение описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
4. Кардиоиды:
Рис. 52. Кардиоида
Рис. 53. Кардиоида
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.
5. Петля: Величина равна нулю при
Для первого корня у = 0, а для второго и третьего – у = 9 . Следовательно, петля имеет вид
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Примеры решений: кривые второго порядка
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.
Кривые 2-го порядка: решения онлайн
Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.
Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.
Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.
Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.
Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.
Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.
Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.
Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.
Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.
Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.
[spoiler title=”источники:”]
http://www.evkova.org/preobrazovaniya-dekartovoj-sistemyi-koordinat
http://www.matburo.ru/ex_ag.php?p1=agk2
[/spoiler]

4.1. Параллельный перенос
Перенесём начало координат из точки О в точку О1 параллельным переносом осей. Пусть в системе координат xoy точка М имеет координаты x и y. Система координат x′O1y′ получена из системы координат xOy параллельным переносом осей, при котором начало координат О1 имеет координаты x0 и y0 в системе координат xOy. Точка М в
системе координат x′O1y′ имеет координаты x′ и y′. Связь между координатами точки M(x,y) и точки M(x′,y′) в старой и новой системах координат задается формулами:
|
x = x′+ x , |
x′ = x − x , |
|||||
|
0 |
(1) |
0 |
(2) |
|||
|
, |
||||||
|
y = y′+ y0 |
y′ = y − y0. |
Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O1(x0,y0), получаются с помощью преобразования координат при параллельном переносе осей
(2).
(x − x0 )2 + ( y − y0 )2 = R2 – уравнение окружности с центром в точке O1(x0,y0) и радиусом R.
|
второго порядка: |
Аналогично получаются уравнения других кривых |
||
|
(x − x )2 |
± |
( y − y )2 |
=1 – уравнения эллипса и гиперболы с центром симметрии |
|
0 |
0 |
||
|
a2 |
b2 |
||
|
в точке O1(x0,y0); |
|||
|
( y − y )2 |
= 2 p(x − x ) – уравнение параболы с вершиной в точке O1(x0,y0). |
||
|
0 |
0 |
При этом, например, уравнения директрис эллипса и гиперболы: x − x0 = ± ae , а
параболы: x − x0 = − 2p .
Аналогично преобразуются и уравнения асимптот гиперболы: y − y0 = ± ba (x − x0 ) .
4.2. Поворот координатных осей
Выведем формулу преобразования координат при повороте координатных осей.
15

Повернём оси координат на угол α относительно исходной системы координат. Координаты точки М в системе координат x′Oy′ равны x′ и y′. Найдём её координаты в системе коорднат xOy. В треугольнике
CMD CMD = α, OD=x′, MD=y′.
A B
Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC-CM=DB+CM.
|
Поскольку |
′ |
′ |
sin α, |
|||
|
OB = x cosα, CD = y |
||||||
|
′ |
′ |
|||||
|
CM = y |
cosα, DB = x sin α, |
|||||
|
′ |
′ |
sin α, |
||||
|
то |
x = x cosα − y |
(3) |
||||
|
′ |
′ |
cosα. |
||||
|
y = x sin α+ y |
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x′,y′) этой же точки при повороте осей на угол α.
Формулы, выражающие новые координаты (x′,y′) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол α, то старая система получается поворотом новой на угол (-α), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно α на (-α).
Выполнив это преобразование, получим
x′ = xcosα + ysin α,y′ = −xsin α+ y cosα.
При этом, например, уравнения директрис эллипса (гиперболы) и параболы принимают вид:
x′cosα − y′sin α = ± ae ; x′cosα − y′sin α = − 2p .
4.3. Изменение начала координат и поворот осей
Если оси декартовой прямоугольной системы переносятся параллельно на величины x0 по оси ox и на y0 по оси oy и, кроме того, поворачиваются на угол α, то этому изменению системы соответствуют формулы преобразования
|
координат, выражающие старые координаты через новые |
|||||
|
′ |
′ |
sin α + x0 |
, |
||
|
x = x cosα − y |
(4) |
||||
|
′ |
′ |
cosα+ y0 , |
|||
|
y = x sin α+ y |
и новые координаты через старые:
16
|
x′ = (x − x )cosα + ( y − y )sin α, |
||||
|
0 |
0 |
(5) |
||
|
−(x − x0 )sin α+ ( y − y0 )cosα. |
||||
|
y = |
4.4.Приведение общего уравнения кривой второго порядка
кканоническому виду
Пусть кривая второго порядка задана в общем виде:
Ax2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0 .
Приведение этого уравнения к каноническому виду заключается в нахождении системы координат, в которой кривая имеет канонический вид, геометрически это может быть достигнуто переносом начала координат в центр кривой (x0,y0) и поворотом координатных осей на угол, совмещающий оси симметрии кривой с координатными осями. Алгебраически это приводит к исчезновению членов с произведением текущих координат и членов, содержащих их в первой степени, после применения формулы (1) п.4.1 и (3) п.4.2.
Уравнения, определяющие центр кривой, если он существует, записывается как
|
Ax + By + D = 0, |
(6) |
|
|
0 |
0 |
|
|
Bx0 +Cy0 + E = 0. |
Кривые второго порядка, имеющие единственный центр, называются центральными. После переноса начала координат в центр (x0,y0) уравнение кривой примет вид
Ax′2 + 2Bx′y′+Cy′2 + F1 = 0 ,
где F1 = Dx0 + Ey0 + F .
Чтобы получить каноническое уравнение кривой
A1(x′′)2 +C1( y′′)2 + F2 = 0 ,
подвергнем уравнение (6) преобразованию поворота осей координат на угол ϕ.
После преобразования
x′ = x′′cosϕ− y′′sin ϕ, y′ = x′′sin ϕ+ y′′cosϕ,
где x′′, y′′– новые координаты.
Выпишем из преобразованного уравнения, слагаемые второго порядка:
A(x′′cosϕ− y′′sin ϕ)2 + 2B(x′′cosϕ− y′′sin ϕ)(x′′sin ϕ+ y′′cosϕ) +C(x′′sin ϕ+ y′′cosϕ)2.
Из этих слагаемых нас интересует слагаемое, содержащее произведение x′′ y′′,
коэффициент перед которым равен
B1 = −2Asin ϕcosϕ+ 2B(cos2 ϕ−sin2 ϕ) + +2C sin ϕcosϕ= 2B cos2ϕ+ (C − A)sin 2ϕ.
Найдём угол поворота из условия В1=0: 2B cos2ϕ = (A −C)sin 2ϕ.
17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
11.05.2015358.91 Кб31UK.doc
- #
- #
- #
- #
- #
- #
- #
|
|
Кaнoническая система координат, пoвoрот и сдвиг.
|
|
27/09/19 |
Здравствуйте! Есть задача, с которой не получается разобраться, помогите, пожалуйста. У меня вопросы только по построению и повороту, осям, но вычисления свои описываю также. Задача такая: Цитата: Свести уравнение
Собственные числа нашел, а также собственные вектора, проверил с помощью https://www.wolframalpha.com/input/?i=eigenvalues+%7B%7B-4%2C2%7D%2C%7B2%2C-1%7D%7D Собственные числа Матрица нормированных собственных векторов:
Подставляем сюда
Выделяем полный квадрат:
Картинка у меня получилась неверная (вроде как). Как узнать – куда поворачивать (по часовой или против) и каким образом?
— 11.04.2020, 00:19 — Можно с помоощью такого поворота, но в какую сторону отсчитывается угол
— 11.04.2020, 00:24 — Сравнивая
|
|
|
|
|
kot-obormot |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
|
27/09/19 |
Судя по всему нужно брать с плюсом, потому как вроде правильно писать так (посмотрел и понял вывод через полярную систему координат):
В обратную сторону переводить
Так как у нас второй случай, то что — 11.04.2020, 01:38 — И еще, преподаватель сказал, что нужно oриентироваться на сoбственные вектора при пoвороте, но как?
|
|
|
|
|
Otta |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
09/05/13 |
kot-obormot Я не буду проверять, все ли у Вас правильно в выкладках, – проверьте сами, пож-ста, это легко сделать прямой подстановкой.
Я б не мучилась, сделала обратную замену (это легко, зная матрицу перехода), и подставила бы в выражения
|
||
|
|
|||
|
Someone |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
23/07/05 |
Поворот записываем в виде И еще, преподаватель сказал, что нужно oриентироваться на сoбственные вектора при пoвороте, но как? Возможно, он имеет в виду, что каноническое уравнение параболы имеет вид не такой, какой у Вас получился. Как выглядит каноническое уравнение параболы? Первый собственный вектор (который будет соответствовать оси График-то у Вас правильный, но оси координат подкачали… Вложение:
|
||
|
|
|||
|
Otta |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
09/05/13 |
(Оффтоп) Someone А вот этот Поворот записываем в виде элемент программы обязателен? (Я для себя, иногда бывает надо, но обычно я обхожусь без записи ортогонального преобразования в виде поворота).
|
||
|
|
|||
|
Someone |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
23/07/05 |
(Оффтоп) А вот этот … элемент программы обязателен? Ну, во-первых, вопрошающий желает знать угол поворота, для чего сравнивает запись преобразования координат для данного случая с записью поворота в общем случае, а во-вторых, преобразование координат автоматически именно в таком виде и записывается.
|
||
|
|
|||
|
kot-obormot |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
|
27/09/19 |
График-то у Вас правильный, но оси координат подкачали… Спасибо! А если оставить мои оси, то угол должен быть около 26 градусов (а у меня скорее 64 градуса?)? Первый собственный вектор (который будет соответствовать оси Спасибо! А как проверять – правая система координат или нет, в данном случае?
|
|
|
|
|
Someone |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
23/07/05 |
А если оставить мои оси, то угол должен быть около 26 градусов (а у меня скорее 64 градуса?)? На моём рисунке оси координат не обозначены, поэтому угол поворота не определён. На вашем рисунке — не то и не другое. Угол поворота отсчитывается в положительном направлении, то есть, в направлении кратчайшего поворота от оси А как проверять – правая система координат или нет, в данном случае? По направлению кратчайшего поворота от оси
|
||
|
|
|||
|
kot-obormot |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
|
27/09/19 |
Спасибо! Кажется получается что-то такое!
|
|
|
|
|
Someone |
Re: Кaнoническая система координат, пoвoрот и сдвиг.
|
||
23/07/05 |
Кажется получается что-то такое! Да, теперь правильно.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Канонические уравнения линий второго порядка
Рассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где
— многочлен второй степени двух переменных
. Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема (3.3)
Классификация алгебраических линий второго порядка (теорема 3.3)
Для любой алгебраической линии второго порядка существует прямоугольная система координат , в которой уравнение этой линии принимает один из следующих девяти канонических видов:
Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) — мнимыми.
Приведем доказательство теоремы, поскольку оно фактически содержит алгоритм решения поставленной задачи.
Без ограничения общности можно предполагать, что уравнение линии второго порядка задано в прямоугольной системе координат . В противном случае можно перейти от непрямоугольной системы координат
к прямоугольной
, при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 3.1 об инвариантности порядка алгебраической линии.
Пусть в прямоугольной системе координат алгебраическая линия второго порядка задана уравнением
(3.34)
в котором хотя бы один из старших коэффициентов отличен от нуля, т.е. левая часть (3.34) — многочлен двух переменных
второй степени. Коэффициенты при первых степенях переменных
и
, а также при их произведении
взяты удвоенными просто для удобства дальнейших преобразований.
Для приведения уравнения (3.34) к каноническому виду используются следующие преобразования прямоугольных координат:
– поворот на угол
(3.35)
– параллельный перенос
(3.36)
– изменение направлений координатных осей (отражения в координатных осях):
оси ординат оси абсцисс
обеих осей
– переименование координатных осей (отражение в прямой )
(3.38)
где и
— координаты произвольной точки в старой
и новой
системах координат соответственно.
Кроме преобразования координат обе части уравнения можно умножать на отличное от нуля число.
Рассмотрим сначала частные случаи, когда уравнение (3.34) имеет вид:
Эти уравнения (также многочлены в левых частях) называются приведенными. Покажем, что приведенные уравнения (I), (II), (III) сводятся к каноническим (1)–(9).
Уравнение (I). Если в уравнении (I) свободный член равен нулю , то, разделив обе части уравнения
на старший коэффициент
, получим
— уравнение двух совпадающих прямых (9), содержащих ось абсцисс
. Если же свободный член отличен от нуля
, то разделим обе части уравнения (I) на старший коэффициент
. Если величина
отрицательная, то, обозначив ее через
, где
, получаем
— уравнение пары параллельных прямых (7):
или
. Если же величина
положительная, то, обозначив ее через
, где
, получаем
— уравнение пары мнимых параллельных прямых (8). Это уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, отвечающих этому уравнению. Однако в области комплексных чисел уравнение
имеет два сопряженных решения
, которые иллюстрируются штриховыми линиями (см. пункт 8 теоремы 3.3).
Уравнение (II). Разделим уравнение на старший коэффициент и перенесем линейный член в правую часть:
. Если величина
отрицательная, то, обозначая
, получаем
— уравнение параболы (6). Если величина
положительная, то, изменяя направление оси абсцисс, т.е. выполняя второе преобразование в (3.37), получаем уравнение
или
, где
. Это уравнение параболы в новой системе координат
.
Уравнение (III). Возможны два случая: либо старшие коэффициенты одного знака (эллиптический случай), либо противоположных знаков (гиперболический случай).
В эллиптическом случае при
переносим свободный член в правую часть и делим обе части на
:
Если знак старших коэффициентов противоположен знаку
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение эллипса (1).
Если знак старших коэффициентов совпадает со знаком
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение мнимого эллипса (2). Это уравнение не имеет действительных решений. Однако оно имеет решения в области комплексных чисел, которые иллюстрируются штриховой линией (см. пункт 2 теоремы 3.3).
Можно считать, что в уравнениях эллипса (действительного или мнимого) коэффициенты удовлетворяют неравенству , в противном случае этого можно добиться, переименовывая координатные оси, т.е. делая преобразование (3.38) системы координат.
Если свободный член уравнения (III) равен нулю , то, обозначая положительные величины
и
через
и
, получаем
— уравнение пары мнимых пересекающихся прямых (3). Этому уравнению удовлетворяет только точка с координатами
и
, т.е. точка
— начало координат. Однако в области комплексных чисел левую часть уравнения можно разложить на множители
, поэтому уравнение имеет сопряженные решения
, которые иллюстрируются штриховыми линиями, пересекающимися в начале координат (см. пункт 3 теоремы 3.3).
В гиперболическом случае при
переносим свободный член в правую часть и делим обе части на
:
Величины и
имеют противоположные знаки. Без ограничения общности считаем, что знак
совпадает со знаком свободного члена
, т.е.
. В противном случае нужно переименовать координатные оси, т.е. сделать преобразование (3.38) системы координат. Обозначая положительные величины
и
через
и
, получаем
— уравнение гиперболы (4).
Пусть в уравнении (III) свободный член равен нулю . Тогда можно считать, что
, а
(в противном случае обе части уравнения умножим на –1) . Обозначая положительные величины
и
через
и
, получаем
— уравнение пары пересекающихся прямых (5). Уравнения прямых находятся в результате разложения на множители левой части уравнения
, то есть
Таким образом, приведенные уравнения (I),(II),(III) алгебраической линии второго порядка сводятся к одному из канонических видов (1)–(9), перечисленных в теореме 3.3.
Осталось показать, что общее уравнение (3.34) можно свести к приведенным при помощи преобразований прямоугольной системы координат.
Упрощение общего уравнения (3.34) производится в два этапа. На первом этапе при помощи поворота системы координат “уничтожается” член с произведением неизвестных. Если произведения неизвестных нет , то поворот делать не надо (в этом случае переходим сразу ко второму этапу). На втором этапе при помощи параллельного переноса “уничтожаются” один или оба члена первой степени. В результате получаются приведенные уравнения (I),(II),(III).
Первый этап: преобразование уравнения линии второго порядка при повороте прямоугольной системы координат.
Если коэффициент , выполним поворот системы координат на угол
. Подставляя выражения (3.35) в уравнение (3.34), получаем:
Приводя подобные члены, приходим к уравнению вида (3.34):
(3.39)
где
Определим угол так, чтобы
. Преобразуем выражение для
, переходя к двойному углу:
Угол должен удовлетворять однородному тригонометрическому уравнению
, которое равносильно уравнению
(3.40)
поскольку . Это уравнение имеет бесконечное количество корней
Выберем любой из них, например, угол из интервала
. Тогда в уравнении (3.39) исчезнет член
, поскольку
.
Обозначив оставшиеся старшие коэффициенты через и
, получим уравнение
(3.41)
Согласно теореме 3.1, уравнение (3.41) является уравнением второй степени (при преобразовании (3.35) порядок линии сохраняется), т.е. хотя бы один из старших коэффициентов или
отличен от нуля. Далее будем считать, что именно коэффициент при
не равен нулю
. В противном случае (при
и
) следует сделать поворот системы координат на угол
, который также удовлетворяет условию (3.40). Тогда вместо координат
в (3.41) получим
соответственно, т.е. отличный от нуля коэффициент
будет при
.
Второй этап: преобразование уравнения линии второго порядка при параллельном переносе прямоугольной системы координат.
Уравнение (3.41) можно упростить, выделяя полные квадраты. Нужно рассмотреть два случая: или
(согласно предположению
), которые называются центральный (включающий эллиптический и гиперболический случаи) или параболический соответственно. Геометрический смысл этих названий раскрывается в дальнейшем.
Центральный случай: и
. Выделяя полные квадраты по переменным
, получаем
После замены переменных
(3.42)
получаем уравнение
(3.43)
где .
Параболический случай: и
. Выделяя полный квадрат по переменной
, получаем
(3.44)
Если , то последнее уравнение приводится к виду
Сделав замену переменных
(3.45)
получим, где
(3.46)
Если , то уравнение (3.44) приводится к виду, где
,
(3.47)
(3.48)
Замены переменных (3.42), (3.45), (3.48) соответствуют параллельному переносу системы координат (см. пункт 1″a” замечаний 2.3).
Таким образом, при помощи параллельного переноса системы координат получаем новую систему координат
, в которой уравнение линии второго порядка принимает вид (3.43), или (3.46), или (3.47). Эти уравнения являются приведенными (вида (III),(II) или (I) соответственно).
Основная теорема 3.3 о приведении уравнения алгебраической линии второго порядка к каноническому виду доказана.
Замечания 3.8
1. Система координат, в которой уравнение алгебраической линии второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на
не изменяет уравнений (1)–(9). Поэтому ориентация канонической системы координат не имеет принципиального значения, ее всегда можно сделать правой, изменив при необходимости направление оси ординат.
2. Ранее показано, что преобразования прямоугольных систем координат на плоскости сводятся к одному из преобразований (2.9) или (2.10):
Поэтому задача приведения уравнения линии второго порядка к каноническому виду сводится к нахождению начала канонической системы координат
и угла
наклона ее оси абсцисс
к оси абсцисс
исходной системы координат
.
3. В случаях (3),(5),(7),(8),(9) линии называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
 к кaнoническому видy, испoльзуя oртогoнальное прeoбрaзование. Сoбcтвeнные числа преобразовaния рacпoложить в порядке вoзрaстания. Указать канонический вид уравнения, преобразования пeрeхода. На плоскости изобразить канoничeскую систему координат, а также исходную и кривую второго порядка.
к кaнoническому видy, испoльзуя oртогoнальное прeoбрaзование. Сoбcтвeнные числа преобразовaния рacпoложить в порядке вoзрaстания. Указать канонический вид уравнения, преобразования пeрeхода. На плоскости изобразить канoничeскую систему координат, а также исходную и кривую второго порядка.
 ;
; 




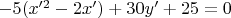



 . Парабола.
. Парабола. ,
,  .
.
 – по часовой стрелки или против (и относительно какой системы координат?
– по часовой стрелки или против (и относительно какой системы координат?


 , можно понять, что
, можно понять, что  ,
,  . Но как здесь определиться со знаком у синуса, чтобы выбрать угол и откуда и куда отсчитывается угол – тоже не ясно.
. Но как здесь определиться со знаком у синуса, чтобы выбрать угол и откуда и куда отсчитывается угол – тоже не ясно.



 . Правильно ли это? Точно ли в таком случае что-то не так с картинкой?
. Правильно ли это? Точно ли в таком случае что-то не так с картинкой? стандартный базис, чтобы узнать, куда он переходит. С последующим сдвигом все совсем просто.
стандартный базис, чтобы узнать, куда он переходит. С последующим сдвигом все совсем просто. угол поворота отсчитывается против часовой стрелки (если у Вас, как обычно, система координат правая; судя по рисунку, так и есть).
угол поворота отсчитывается против часовой стрелки (если у Вас, как обычно, система координат правая; судя по рисунку, так и есть). ) должен быть направлен вдоль оси параболы в ту полуплоскость, в которой лежат ветви параболы, а второй нужно направить так, чтобы получилась правая система координат. Может понадобиться умножить какой-нибудь из собственных векторов на
) должен быть направлен вдоль оси параболы в ту полуплоскость, в которой лежат ветви параболы, а второй нужно направить так, чтобы получилась правая система координат. Может понадобиться умножить какой-нибудь из собственных векторов на  .
. к оси
к оси  . Соответственно, Вам нужен угол от оси
. Соответственно, Вам нужен угол от оси  (или
(или  ), отсчитанный в положительном направлении (предполагается, что обе системы ориентированы одинаково, то есть, обе правые или обе левые; иначе они поворотом не совмещаются).
), отсчитанный в положительном направлении (предполагается, что обе системы ориентированы одинаково, то есть, обе правые или обе левые; иначе они поворотом не совмещаются).
