Как найти угол поворота кривой

Для
построения профиля необходимо вычислить
элементы кривой: Т –
тангенс,
К – кривая, Д – домер, Б – биссектриса.

Элементы кривой
вычисляются по формулам:

Тангенс
; Кривая;

Домер
; Биссектриса

,

где R
– радиус
кривой, м; 
– угол
поворота трассы.

Пример вычисления
элементов кривой.

В
примере вершина угла поворота пк 4 + 33,
угол поворота 
= 43
26
и радиус кривой R
= 150 м.

Тангенс

м;

Кривая
м;

Домер
м;

Биссектриса
м.

2.7 Вычисление пикетажного значения главных точек кривой

Главные
точки кривой – это начало кривой (НК),
середина кривой (СК) и конец кривой (КК).
Пикетажное значение показывает расстояние
от начала трассы (НТ) до соответствующей
точки.

Вычисление
пикетажного значения главных точек
кривой выполняется по формулам:

пк НК = пк ВУ – Т;

пкКК = пкНК + К;

пкСК = пкНК +0,5К

Контроль: пкКК =
пкВУ + Т – Д;

пкКК = пкСК +0,5К.

Пример вычисления
пикетажных значений главных точек
кривой.

По
приведенным исходным данным пикетажные
значения главных точек кривой принимают
значения:

пк НК = пк ВУ – Т =
пк 4+33 – 59,74 = 3+73,26

пкКК
= пкНК + К = 373,26 + 113,65 = 486,91

пкСК
= пкНК +0,5К = пк 3+73,26 + 0,5 
113,65 = 430,08

Контроль:

пкКК
= пкВУ + Т – Д = пк 4 +33 +59,74 – 5,83 = 486,91

пкКК
= пкСК +0,5К = 430,08 + 0,5 
113,65 = 486,90

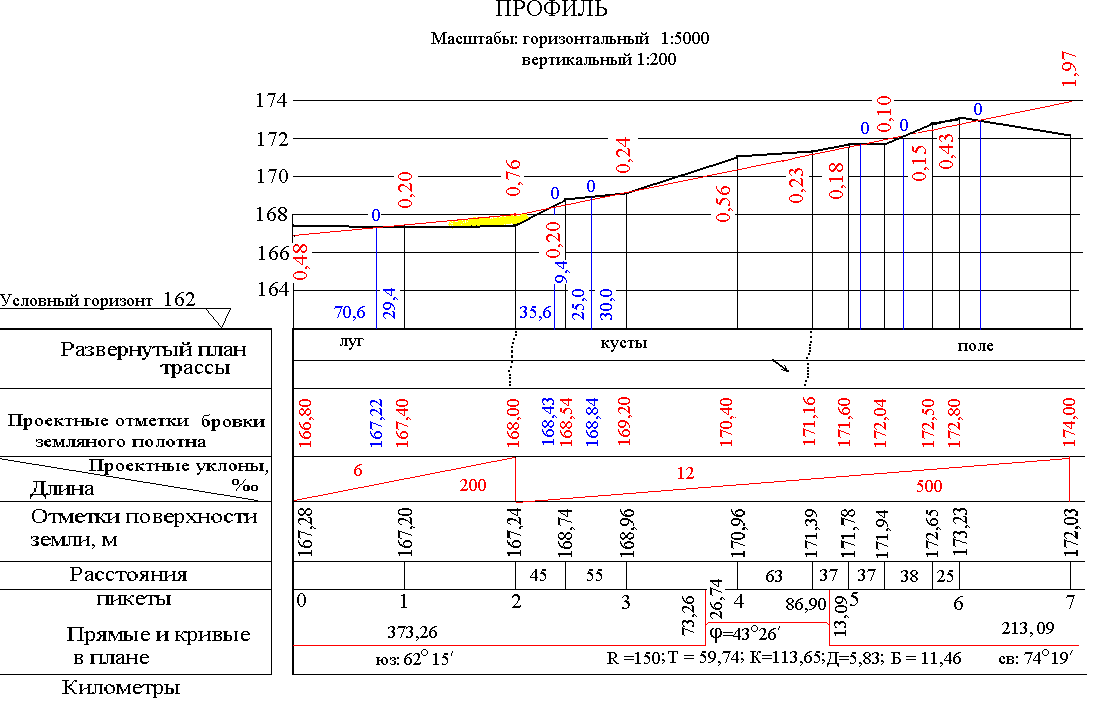
2.8 Построение продольного профиля

Профиль строится
на миллиметровой бумаге формата А3.
Масштаб для построения продольного
профиля по горизонтали и вертикали
различный. Для обеспечения наглядности
обычно вертикальный масштаб в 10 раз
крупнее горизонтального. В индивидуальном
задании указываются масштабы для
построения профиля. Профиль строится
с использованием специальной таблицы
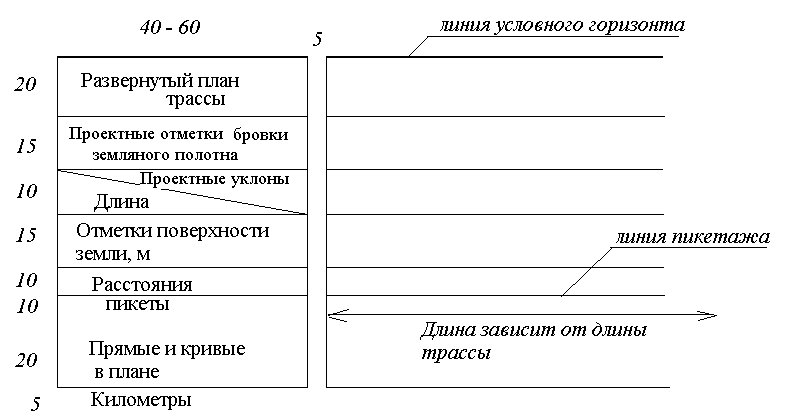
– сетки профиля. Ее размеры (в мм) и графы
приведены на рис.
7.

Рис 7. Сетка профиля

Профиль располагается
выше сетки профиля. При его построении
это необходимо учесть. Общий вид профиля
приведен на рис. 9.

Построение профиля
начинается с графы «Расстояния».
В этой графе указываются пикетные и
плюсовые точки. С учетом горизонтального
масштаба строятся полные пикеты по 100
м. В графе они отмечаются вертикальными
линиями. Если между пикетами есть
плюсовые точки, они также наносятся в
эту графу и подписываются расстояния
между ними (рис. 8).

Рис. 8. Заполнение
графы «Расстояния» и «Пикеты»

В примере, между
пикетами 5 и 6 расположены две плюсовые
точки: +37 и +75. Расстояния подписываются
37и38(75 – 37 = 38 м) и25(100 – 75
м). Сумма отрезков 37 + 38 + 25 = 100 м (Рис.8).

Затем заполняется
графа «Пикеты».
В этой графе подписываются пикеты около
вертикальных линий, начиная с пикета 0
(пк0) (рис. 8).

Графа «Развернутый
план трассы»
заполняется по данным пикетажа
(пикетажной книжки). По середине графы
проводится ось дороги условно развернутая
в прямую линию. Вдоль линии наносится
план местности, прилегающий к трассе и
все объекты, которые находятся в полосе
25 м влево и вправо от оси трассы,
показываются границы между угодьями и
строения. В точках, соответствующих
вершинам углов поворота показывается
направление поворота трассы (вправо
или влево). Вместо условных знаков
допускается писать соответствующее
название: «луг», «лес» и т. д. (рис. 10).

Рис. 10. Заполнение
графы «Развернутый план трассы»

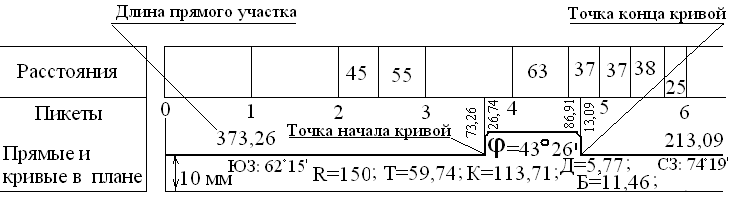
Графа «Прямые
и кривые в плане»
заполняется по результатам вычисления
пикетажных значений главных точек
кривых (Рис.11). В графе проводится прямая
линия на расстоянии 10 мм от нижней
границы. По пикетажному значению точки
«Начало кривой» она наносится на профиль
с учетом горизонтального масштаба на
линии пикетажа. От линии пикетажа
опускается перпендикуляр на ось дороги,
которая проводится вдоль графы. До точки
«Начало кривой» трасса показывается
прямой линией. Аналогично показывается
точка «Конец кривой». От нее трасса так
же показывается прямой. Между точками
«Начало кривой» и «Конец кривой» ось
дороги прерывается и кривая показывается
скобой. Если поворот правый, то скоба
направлена вверх, если поворот левый,
то скоба обращена вниз.

Рис. 11. Заполнение
графы «Прямые и кривые в плане»

Вдоль перпендикуляров
от пикетажной линии до оси дороги у
точек «Начало кривой» и «Конец кривой»
подписываются расстояния от заднего
пикета до точки и от точки до переднего
пикета.

Внутри кривой
выписываются угол поворота трассы ,
радиус R,
тангенс Т, кривая К, домер Д, биссектриса
Б.

Над
серединой каждой прямой вставки
записывают ее длину, а под ней дирекционный
угол или румб. Начальное направление
трассы выдается в задании. После поворота
трассы направление меняется. Ориентирующий
угол вычисляется по формулам зависимости
дирекционного угла и румба. В нашем
примере применяется формула второй
четверти:

_пк0-НК
= r
+ 180
= 6215
+ 180
= 24215;

_КК-ПК7
= _пк0-НК
+
= 43
26
= 285
41.
r
= 360
– 285
41
= 7419(сз).

Графа «Отметки
земли»
заполняется из «Ведомости геометрического
нивелирования». Отметки выписываются
к соответствующим пикетам и плюсовым
точкам с точностью 0,01 м.

ВНИМАНИЕ: «иксовые»
точки в построении не участвуют и их
отметки не
выписываются (рис.
2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Круговые кривые. Железнодорожные линии (также и автомобильные дороги) в плане состоят из прямолинейных участков, сопряжённых между собой кривыми. Наиболее простой и распространённой формой кривой является дуга окружности. Такие кривые носят название круговых кривых. На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400 и 300 м. Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями.

Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).

Рис. 15.3 Схема круговой кривой

Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:

– тангенс кривой Т (или касательная) – отрезок прямой между вершиной угла и началом или концом кривой;

– кривая К – длина кривой от начала кривой до её конца;

– биссектриса кривой Б – отрезок от вершины угла до середины кривой;

– домер Д – разность между длиной двух тангенсов и кривой.

Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):

Т = R×tg(a/2); К = R×a = p R a°¤180°; Б = R [sec(a/2) – 1], (15.1)

где a° – угол поворота в градусах.

Домер вычисляют по формуле

. (15.2)

Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.

В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:

ПК НК = ПК ВУ – Т; ПК КК = ПК НК + К; ПК СК = ПК НК + К/2. (15.3)

Правильность вычислений контролируют по формулам:

ПК КК = ПК ВУ + Т – Д; ПК СК = ПК ВУ + Д/2. (15.4)

Пример.

Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.

По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.

Вычислим пикетажное положение главных точек:

Контроль:

ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00

– Т 96,73 + Т 96,73

ПК НК 5 + 39,27 7 + 32,73

+ К 1 + 91,81 – Д 1,65

ПК КК 7 + 31,08 ПК КК 7 + 31,08

ПК НК 5 + 39,27 ПК ВУ 6 + 36,00

+ К/2 95,90 – Д/2 0,82

ПК СК 6 + 35,17 ПК СК 6 + 35,18

Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим

,

где s и r – текущие значения расстояния от начала переходной кривой и ее радиуса кривизны;

R – радиус кривизны в конце переходной кривой.

Индексом k отмечены значения переменных в конце переходной кривой.

Для радиуса кривизны переходной кривой в текущей точке i найдём:

r = lR/s, (15.5)

где через l обозначена длина переходной кривой s_k. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.

Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол

.

Подставляя выражение радиуса кривизны r из (15.5), получим

.

Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:

,

откуда

Rlj = s²/2.

б)

а)

Рис. 15.4 Схема переходной кривой:

а – углы поворота трассы: φ – в текущей точке i, β – в конце

переходной кривой (точка КПК); б – приращения координат

Из полученного уравнения вытекают формулы:

; ; l = 2Rb, (15.6)

где b – угол поворота трассы в конце переходной кривой;

l – длина переходной кривой;

R – радиус кривизны в конце переходной кривой, равный радиусу следующей за нею круговой кривой.

Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):

dx = cosj×ds; dy = sinj×ds. (15.7)

Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):

cosj = 1-j²/2 = 1 – s⁴/(8R²l²);

sinj = j – j³/6 = s²/(2Rl) – s⁶/(48R³l³).

Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:

; (15.8)

. (15.9)

Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:

,

где x_КПК и y_КПК – координаты конца переходной кривой, вычисляемые по формулам (15.8) и (15.9) с аргументом s = l .

Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.

Рис. 15. 5 Смещение начала переходной кривой	Рис. 15.6 Сопряжение круговой кривой с переходными

Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q₁ и имеющая длину K = Ra.

При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна

K_c = R (a-2b) + 2l = Ra – 2Rb + 2l = K – l + 2l = K + l.

Тангенс и биссектриса определяются по формулам:

Т_с = T + m + T_p; Б_c = Б + Б_p,

где Т_p = ptg(a/2); Б_p = psec(a/2).

Домер в этом случае равен

.

В полевых условиях значения m, Т_p и Б_p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).

Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 – 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 – 9y 2 -64x – 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Преобразования декартовой системы координат с примерами решения

Содержание:

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол (Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы к каноническому виду.

Решение:

Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка – начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

2. Уравнение окружности: уравнение описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

3. Уравнение описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего – у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Бесконечно малые и бесконечно большие функции
• Замечательные пределы
• Непрерывность функций и точки разрыва
• Точки разрыва и их классификация
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

[spoiler title=”источники:”]

http://www.evkova.org/preobrazovaniya-dekartovoj-sistemyi-koordinat

http://www.matburo.ru/ex_ag.php?p1=agk2

[/spoiler]

Расчет элементов кривой. Тангенсы, хорда, биссектриса, домер, длина кривой.

Опубликовано 6 лет назад. Просмотров с момента размещения на сайте 109887

Также, Вас может заинтересовать: