Как найти угол поворота осей координат - Сайт, где вы сможете решить свои вопросы

В
аналитической геометрии часто применяется
преобразование координат, называемое
поворотом
осей. Оно
заключается в следующем: обе оси координат
поворачиваются в одну сторону на один
и тот же угол, а начало координат остается
неизменным. Примеры использования этого
преобразования будут даны в следующих
двух параграфах.

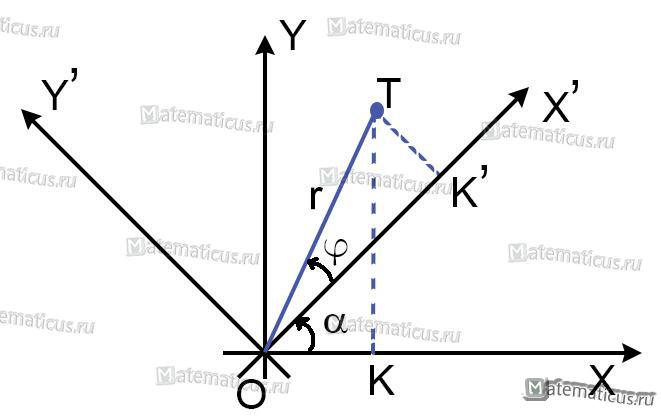
Пусть
оси координат повернуты на угол

(рис. 3.14). Угол

– это угол, на который нужно повернуть
старую ось

до ее совмещения с новой осью

;
угол

считается положительным при повороте
против часовой стрелки.

Выведем
формулы, позволяющие выразить старые
координаты

любой точки

через ее новые координаты

и

.

Для
этого построим радиус-вектор

точки

и обозначим через

углы, образованные им соответственно
с осями

:
точка

имеет полярные координаты

,
если за полярную ось принять ось

,
и координаты

,
если за полярную ось принять ось

Углы

связаны равенством

.
Выражая декартовы координаты точки

через ее полярные координаты, имеем:

(А)

(Б)

Заменяя
в формулах (А)

на

и используя формулы для синуса и косинуса
суммы двух углов, находим:

Отсюда,
используя формулы (Б), находим следующие
формулы, выражающие старые координаты

через
новые координаты

(3.42)

Формулы обратного
перехода, выражающие новые координаты
через старые, мы получим аналогичным
путем из формул (Б), заменяя в них угол

на

:

(3.42′)

Формулы
(3.42′)
можно получить также из соотношений
(3.42), рассматривая их как уравнения,
определяющие

через

,
и разрешая их относительно

Формулы
(3.42′)
можно было бы получить из формул (3.42)
еще и следующим путем: поменять в формулах
(3.42) местами

,
а также

и заменить

на

(так как новые оси получаются из старых
поворотом на угол

,
то и старые оси могут быть получены из
новых поворотом в обратную сторону, т.
е. на угол

Рекомендуем
читателю получить формулы (3.42′)
этими двумя способами.

§ 3.9. Исследование общего уравнения кривой второго порядка Наиболее общее уравнение второй степени относительно и имеет вид:

(3.49)

В
аналитической геометрии его называют
общим уравнением кривой второго порядка.
От уравнения:

уравнение
(3.49) отличается наличием члена с
произведением координат, т. е. коэффициент

мы считаем не равным нулю.

В
настоящем параграфе наша задача –
показать, что и уравнение (3.49), так же,
как и уравнение (3.39), может определять
только одну из изученных нами ранее
кривых – эллипс, гиперболу или параболу
(с возможными для каждого из них случаями
вырождения), найти способ по виду
уравнения (3.49) установить тип определяемой
им кривой (подобно тому, как это делалось
для уравнения (3.39) по знаку произведения

)
и научиться для каждого конкретного
уравнения (3.49) строить кривую.

Наиболее
простой способ решения этой задачи –
при помощи поворота координатных осей
на некоторый угол

преобразовать уравнение (3.49) в уравнение
вида (3.39) по отношению к новой системе
координат, поскольку уравнение (3.39) нами
уже изучено во всех подробностях.

Итак,
повернем координатные оси на некоторый
угол

.
Новые оси координат обозначим через

и

.
Тогда старые координаты будут выражаться
через новые по формулам (3.42) так:

Подставляя
эти значения

в уравнение (3.49), после приведения
подобных членов приведем его к виду:

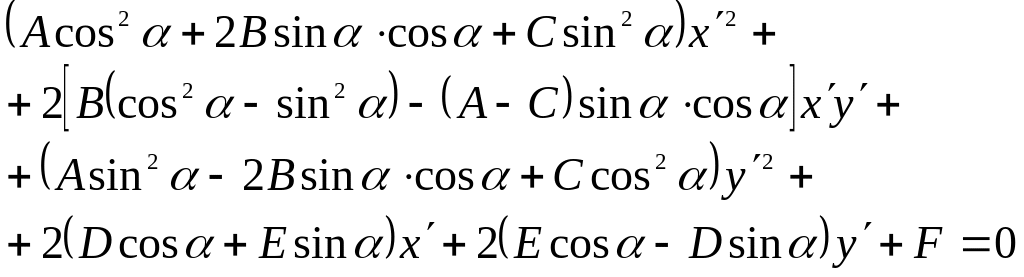
(3.50)

Уравнение (3.50) имеет
ту же структуру, что и уравнение (3.49).
его можно записать в виде:

(3.50′)

где

(3.51)

(Значения
новых коэффициентов

и

,
несущественные для дальнейшего, мы не
описываем.)

Выберем
теперь угол

таким, чтобы новый коэффициент

в уравнении (3.50′)
обратился бы в нуль; это дает нам для
определения угла

уравнение:

(3.52)

откуда
находим:

(3.53)

Формула
(3.53) определяет два значения угла

,
разность между которыми равна

;
поэтому безразлично, какое из них
выбрать: переход от одного к другому
равносилен перестановке новых осей
координат

После
того, как угол

определен по формуле (3.53), уравнение
(3.50′)
приводится к виду:

(3.54)

и,
как нам известно, определяет эллипс
(окружность), гиперболу или параболу
(или вырождения этих кривых) в зависимости
от знака произведения

(см. § 3.6.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Исходим из уравнения

(1)

И покажем, что всегда можно выбрать угол поворота координатных осей так, что “смешанный” член обратится в нуль. Пусть система координат X”O’y” получена поворотом системы X’O’y’ вокруг начала O’ на угол .

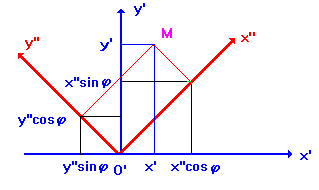
Как видно из рисунка, “старые” и “новые” координаты связаны равенствами

(2)

Подставим их в уравнение (1)

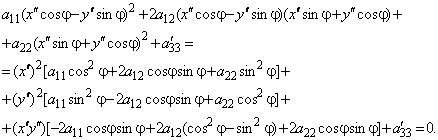Последнюю квадратную скобку перепишем в виде и выберем угол j так, чтобы она обращалась в нуль:

Разделим это уравнение на , получим . Откуда найдем искомый угол

. (3)

Обозначая в (2) первые квадратные скобки , а вторые , получим уравнение (20.4) в “новой” системе координат

. (4)

ВЫВОД: Для кривой, заданной уравнением (1), поворотом осей координат можно “уничтожить” смешанный (билинейный) член и преобразовать его к уравнению (4); при этом свободный член не изменяется.

Пример 1. Поворотом осей координат установить тип кривой, заданной уравнением

Сравнивая с уравнением (20.4), находим

По формуле (3) найдем угол поворота .

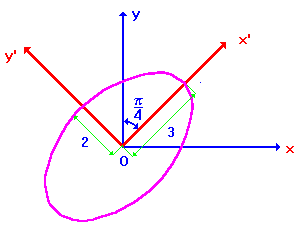
Итак, для приведения кривой к каноническому виду следует сделать поворот осей на угол , при этом формулы перехода даются (2):

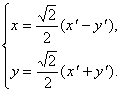
Подставим эти значения в исходное уравнение, получим

Разделим уравнение на свободный член и перенесем его в правую часть уравнения, получим – это эллипс с полуосями .

< Предыдущая		Следующая >

Источник

Чтобы найти поворот осей, зададим две системы координат, согласно рисунку

Пусть точка T в новой полярной системе координат имеет полярный радиус r и полярный угол φ. В старой полярной системе координат полярный угол точки T будет равен α+φ, а полярный радиус r будет как в новой системе координат.

Тогда уравнения примут вид:

x = r cos(α+φ)

y = r sin(α+φ)

Применяя тригонометрические тождества суммы двух углов для синуса и косинуса , получим выражения:

x = r (cosα cosφ — sinα sinφ) = r (cosφ) cosα — (r sinφ) sinα

y = r (sinα cosφ + cosα sinφ) = r (cosφ) sinα + (r sinφ) cosα

Обозначим

X = r cosφ и Y = r sinφ

Получим уравнения поворота осей координат

x = X cosα — Y sinα

y = X sinα + Y cosα

Если обозначим следующим образом

x = OK , y = KT — старые координаты точки T
x´= OK´, y´ = KT´ — новые координаты точки T
α — угол поворота осей

тогда формулы поворота осей координат примут вид:

Пример
До поворота осей на угол -30⁰ точка L имела абсциссу x=2 и ординату y=0

Требуется найти координаты точки L после поворота осей.

Решение
Подставляя в формулу, находим новые координаты осей x´, y´

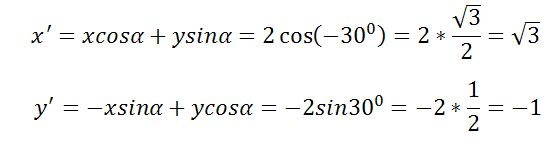
12750

Источник

Макеты страниц

Пусть на плоскости заданы две системы координат, имеющие общее начало О: система Оху (старая) и система OXY (новая), которая получена поворотом старой системы на угол а. Это значит, что угол (рис. 34) и, следовательно, угол .

Рис. 34

Найдем формулы, выражающие старые координаты х и у произвольной точки М плоскости через ее новые координаты X и Y.

Введем полярные координаты: старые — с полярной осью, совпадающей с осью и новые — с полярной осью, совпадающей с осью ОХ. Пусть точка М в новой полярной системе имеет полярный угол и полярный радиус . В старой полярной системе полярный угол точки М будет равен полярный радиус будет таким же, как и в новой системе.

Поэтому по формулам (7) будем иметь:

Используя тригонометрические тождества для косинуса и синуса суммы двух углов, получим:

Но , поэтому

Формулы (19) называются формулами поворота осей.

Пример. Выразить старые координаты точки х и у через ее новые координаты X и Y при повороте осей на угол .

Решение. Так как по формулам (19) получим:

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2023 года; проверки требуют 2 правки.

Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица^[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.

Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.

Матрица поворота в двумерном пространстве[править | править код]

В двумерном пространстве поворот можно описать одним углом ;theta со следующей матрицей линейного преобразования в декартовой системе координат:

$M(theta )={begin{pmatrix}cos {theta }&mp sin {theta }\pm sin {theta }&cos {theta }end{pmatrix}}$

или

${displaystyle M(theta )=exp left({theta }cdot {begin{bmatrix}0&mp 1\pm 1&0end{bmatrix}}right)}$

Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:

${displaystyle {begin{bmatrix}x'\y'\end{bmatrix}}={begin{bmatrix}cos theta &mp sin theta \pm sin theta &cos theta \end{bmatrix}}{begin{bmatrix}x\y\end{bmatrix}}.}$

Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:

{displaystyle x'=xcos theta mp ysin theta ,}

{displaystyle y'=pm xsin theta +ycos theta .}

Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).

Матрица поворота в трёхмерном пространстве[править | править код]

Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.

Матрицами вращения вокруг оси декартовой системы координат на угол varphi в трёхмерном пространстве с неподвижной системой координат являются:

Вращение вокруг оси :

${displaystyle M_{x}(varphi )={begin{pmatrix}1&0&0\0&cos varphi &-sin varphi \0&sin varphi &cos varphi end{pmatrix}}.}$

Вращение вокруг оси :

${displaystyle M_{y}(varphi )={begin{pmatrix}cos varphi &0&sin varphi \0&1&0\-sin varphi &0&cos varphi end{pmatrix}}.}$

Вращение вокруг оси :

${displaystyle M_{z}(varphi )={begin{pmatrix}cos varphi &-sin varphi &0\sin varphi &cos varphi &0\0&0&1end{pmatrix}}.}$

Матрица поворота последовательности поворотов в некотором оговорённом порядке:

${displaystyle M_{x}(alpha )*M_{y}(beta )*M_{z}(gamma )={begin{pmatrix}1&0&0\0&cos alpha &-sin alpha \0&sin alpha &cos alpha end{pmatrix}}{begin{pmatrix}cos beta &0&sin beta \0&1&0\-sin beta &0&cos beta end{pmatrix}}{begin{pmatrix}cos gamma &-sin gamma &0\sin gamma &cos gamma &0\0&0&1end{pmatrix}}={begin{pmatrix}cos beta cos gamma &-sin gamma cos beta &sin beta \sin alpha sin beta cos gamma +sin gamma cos alpha &-sin alpha sin beta sin gamma +cos alpha cos gamma &-sin alpha cos beta \sin alpha sin gamma -sin beta cos alpha cos gamma &sin alpha cos gamma +sin beta sin gamma cos alpha &cos alpha cos beta end{pmatrix}}.}$

Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси^[2]. Например, при повороте на угол ${displaystyle alpha =90^{circ }}$ вокруг оси ось переходит в : ${displaystyle M_{z}(90^{circ })cdot mathbf {e} _{x}=mathbf {e} _{y}}$ . Аналогично, ${displaystyle M_{y}(90^{circ })cdot mathbf {e} _{z}=mathbf {e} _{x}}$ и ${displaystyle M_{x}(90^{circ })cdot mathbf {e} _{y}=mathbf {e} _{z}}$ . Правая система координат связана с выбором правого базиса (см. правило буравчика).

Матрица поворота в n-мерном пространстве[править | править код]

Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.

Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости^[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.

Итак, аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.

Например:

$M_{1,2}(alpha )={begin{pmatrix}cos alpha &-sin alpha &0&0&0\sin alpha &cos alpha &0&0&0\0&0&1&0&0\0&0&0&1&0\0&0&0&0&1end{pmatrix}}$

— матрица поворота в 5-мерном пространстве в плоскости $x_{1}x_{2}$ ,

$M_{2,4}(alpha )={begin{pmatrix}1&0&0&0&0&0&0\0&cos alpha &0&-sin alpha &0&0&0\0&0&1&0&0&0&0\0&sin alpha &0&cos alpha &0&0&0\0&0&0&0&1&0&0\0&0&0&0&0&1&0\0&0&0&0&0&0&1end{pmatrix}}$

— матрица поворота в 7-мерном пространстве в плоскости $x_{2}x_{4}$ .

Изменение оси поворота[править | править код]

Пусть — матрица поворота вокруг оси с ортом на угол ;alpha , ;M' — матрица поворота вокруг оси с ортом ;n' на тот же угол, причем

где ;M'' — матрица поворота, изменяющая орт оси поворота . Тогда

$M'=M''cdot Mcdot M''^{;T},$

где $;M''^{{;T}}$ — транспонированная матрица ;M'' .

Перестановочность поворотов[править | править код]

Если $;M_{1}$ — матрица поворота вокруг оси с ортом на угол ;alpha , $;M_{2}$ — матрица поворота вокруг оси с ортом на угол ;beta ,
то $M_{2}cdot M_{1}$ — матрица, описывающая поворот, являющийся результатом двух последовательно осуществленных поворотов ( $;M_{1}$ и $;M_{2}$ ), поскольку

$(M_{2}cdot M_{1})cdot r=M_{2}cdot (M_{1}cdot r).$

При этом последовательность поворотов можно поменять, видоизменив поворот $;M_{1}$ :

$M_{2}cdot M_{1}=M'_{1}cdot M_{2},$

где матрица $;M'_{1}$ — матрица поворота на угол ;alpha вокруг оси c ортом ;n', повернутым с помощью поворота $;M_{2}$ :

$n'=M_{2}cdot n,qquad M'_{1}=M_{2}cdot M_{1}cdot M_{2}^{T},$

поскольку $M_{2}^{T}cdot M_{2}=E$ , так как матрица поворота является ортогональной матрицей ( — единичная матрица). Заметим, что коммутативности поворотов в обычном смысле нет, то есть

$M_{2}cdot M_{1}neq M_{1}cdot M_{2}.$

Выражение матрицы поворота через углы Эйлера[править | править код]

Последовательные повороты около осей на угол прецессии ( alpha ), угол нутации ( beta ) и на угол собственного вращения ( gamma ) приводят к следующему выражению для матрицы поворота:

${displaystyle M(alpha ,beta ,gamma )={begin{pmatrix}cos alpha cos gamma -sin alpha cos beta sin gamma &-cos alpha sin gamma -sin alpha cos beta cos gamma &sin alpha sin beta \sin alpha cos gamma +cos alpha cos beta sin gamma &-sin alpha sin gamma +cos alpha cos beta cos gamma &-cos alpha sin beta \sin beta sin gamma &sin beta cos gamma &cos beta end{pmatrix}}.}$

Ось ;X' — ось X, повёрнутая первым поворотом (на ;alpha ), ;Z'' — ось Z, повёрнутая первым и вторым поворотом (на ;alpha и ;beta ). Вследствие перестановочности поворотов приведённая матрица соответствует поворотам на углы ;gamma , ;beta , ;alpha вокруг осей Z, X, Z:

${displaystyle M(alpha ,beta ,gamma )=M_{Z}(alpha )cdot M_{X}(beta )cdot M_{Z}(gamma )}$

В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:

1) Поворот около осей:
2) Соответственно:
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)

Матрица поворота вокруг произвольной оси[править | править код]

Пусть ось вращения задана единичным вектором , а угол поворота theta .

Тогда матрица поворота в декартовых координатах имеет вид:

$M({hat {mathbf {v} }},theta )={begin{pmatrix}cos theta +(1-cos theta )x^{2}&(1-cos theta )xy-(sin theta )z&(1-cos theta )xz+(sin theta )y\(1-cos theta )yx+(sin theta )z&cos theta +(1-cos theta )y^{2}&(1-cos theta )yz-(sin theta )x\(1-cos theta )zx-(sin theta )y&(1-cos theta )zy+(sin theta )x&cos theta +(1-cos theta )z^{2}end{pmatrix}}$

Выражение матрицы поворота через кватернион[править | править код]

Если задан кватернион , то соответствующая матрица поворота имеет вид:

$Q={begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}end{bmatrix}}.$

Свойства матрицы поворота[править | править код]

Если — матрица, задающая поворот вокруг оси на угол varphi , то:

Примечания[править | править код]

См. также[править | править код]

Матрица перехода
Поворот

Литература[править | править код]

Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.

Ссылки[править | править код]

Поворот плоскости. Матрица поворота

Источник

§ 3.9. Исследование общего уравнения кривой второго порядка Наиболее общее уравнение второй степени относительно и имеет вид:

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://www.matematicus.ru/wp-content/uploads/2017/12/Povorot-osej.jpg" alt="Поворот осей" width="661" height="416" />

Если обозначим следующим образом

Матрица поворота в двумерном пространстве[править | править код]

Матрица поворота в трёхмерном пространстве[править | править код]

Матрица поворота в n-мерном пространстве[править | править код]

Изменение оси поворота[править | править код]

Перестановочность поворотов[править | править код]

Выражение матрицы поворота через углы Эйлера[править | править код]

Матрица поворота вокруг произвольной оси[править | править код]

Выражение матрицы поворота через кватернион[править | править код]

Свойства матрицы поворота[править | править код]

Примечания[править | править код]

См. также[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Армейские друзья как найти

Как найти свою реферальную ссылку вот

Как найти контакты в вайбере на компьютере

Добавить комментарий Отменить ответ