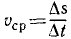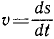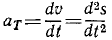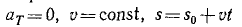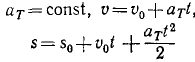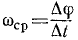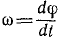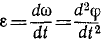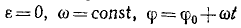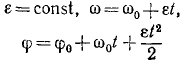Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
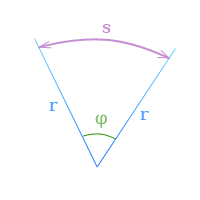
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
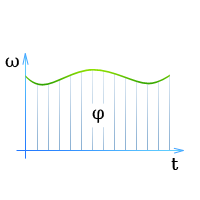
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|
Содержание:
Вращение твердого тела вокруг неподвижной оси:
Вращением тела вокруг неподвижной оси называется такое его движение, при котором две точки тела, например А и В, неподвижны (рис. 162). Прямая, проходящая через указанные две неподвижные точки, называется осью вращения. Если мысленно провести через тело две полуплоскости — неподвижную 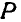
Рис. 162.
При вращении тела угол поворота его 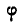 изменяется с течением времени, а поэтому он является функцией времени:
изменяется с течением времени, а поэтому он является функцией времени:
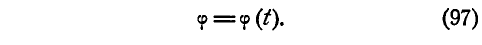
Уравнение (97) называется уравнением вращения; зная его, можно для любого момента t найти угол 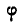 , а следовательно, и положение вращающегося тела.
, а следовательно, и положение вращающегося тела.
Величины угловой скорости и углового ускорения тела, вращающегося вокруг неподвижной оси, определяются по формулам (87) и (90).
Если 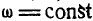 , то такое вращение тела называется равномерным и уравнение вращения его (97) напишется аналогично уравнению (71) расстояний точки, движущейся равномерно:
, то такое вращение тела называется равномерным и уравнение вращения его (97) напишется аналогично уравнению (71) расстояний точки, движущейся равномерно:
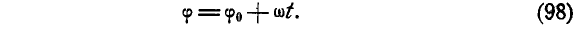
Поэтому такое уравнение по аналогии с равномерным движением точки называется уравнением равномерного вращения.
Точно так же, если 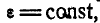 то вращение тела называется равнопеременным.
то вращение тела называется равнопеременным.
Уравнения равнопеременного вращения тела могут быть выведены аналогично уравнениям (82) и (83) равнопеременного движения точки путем замены линейных характеристик угловыми и записаны в виде:
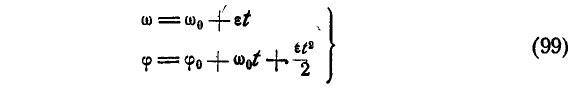
Условимся угловую скорость вращающегося тела изображать вектором, отложенным по оси вращения в такую сторону, чтобы, смотря с конца этого вектора, вращение тела происходило в направлении, противоположном движению часовой стрелки (рис. 163).
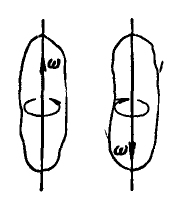
Рис. 163.
При вращении тела вокруг неподвижной оси (рис. 164) любая точка его М, отстоящая на расстоянии h от оси вращения, описывает окружность радиуса h и имеет линейную скорость, определяемую формулой (89): 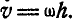
Если провести из любой точки О оси радиус-вектор в точку М, то вектор линейной скорости точки М может быть представлен также в виде векторного произведения  на
на 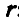 :
:
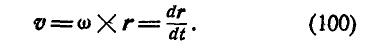
В самом деле, раскрывая векторное произведение, получим величину скорости, определяемую формулой (89):
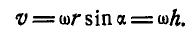
Вектор же скорости направлен перпендикулярно к плоскости векторов 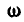 на
на 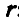 в такую сторон, чтобы обход контура параллелограмма, построенного на
в такую сторон, чтобы обход контура параллелограмма, построенного на 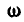 на
на 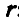 , задаваемый первым вектором
, задаваемый первым вектором 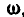 , стоящим в векторном произведении, происходил против часовой стрелки, что согласуется с определением векторного, произведения двух векторов.
, стоящим в векторном произведении, происходил против часовой стрелки, что согласуется с определением векторного, произведения двух векторов.
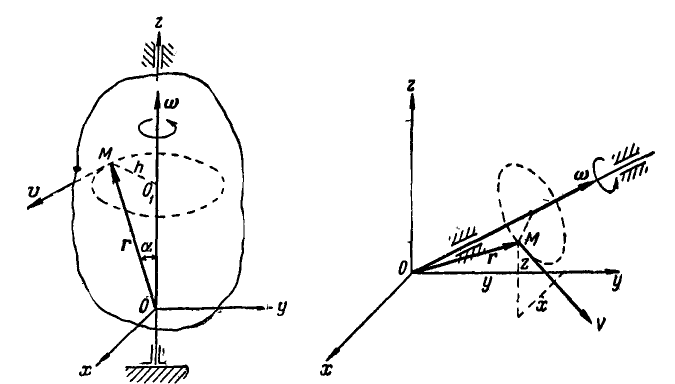
Рис. 164. Рис. 165.
В самом общем случае, когда ось вращения тела составляет любые углы с координатными осями (рис. 165), проекции скорости точки М могут быть найдены по формулам проекций векторного произведения двух векторов (11):
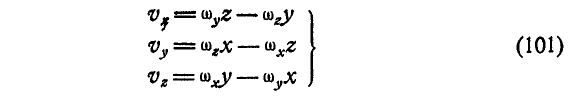
Равенства (101) называются формулами Эйлера. Здесь 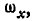
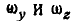 — проекции
— проекции 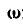 ; а
; а 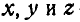 —проекции
—проекции 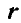 на координатные оси.
на координатные оси.
Если ось вращения вертикальна (рис. 164), то 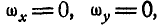
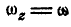 и формулы Эйлера принимают вид:
и формулы Эйлера принимают вид:
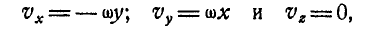
что было получено нами раньше (88). Мы уже знаем, что величина углового ускорения 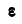 определяется по формуле (90).
определяется по формуле (90).
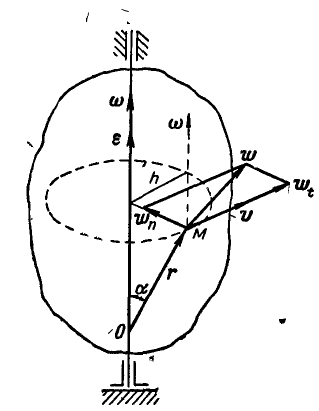
Рис. 166.
Введем в рассмотрение вектор углового ускорения е, под которым мы будем понимать векторную величину:
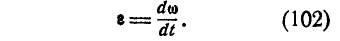
Так как 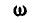 имеет постоянное направление, то вектор
имеет постоянное направление, то вектор 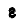 всегда совпадает с осью вращения.
всегда совпадает с осью вращения.
При 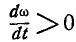 векторы
векторы 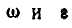 — одного направления;
— одного направления;
при 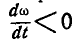 векторы
векторы 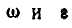 — противоположных направлений.
— противоположных направлений.
Нормальное и касательное ускорения любой точки М вращающегося тела (рис. 166) Moryт быть найдены по формулам (91):
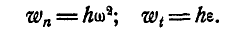
Дадим векторное обобщение этим величинам. В самом общем случае вектор ускорения может быть найден по формуле (79):
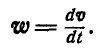
Принимая во внимание формулы (100) и (102), имеем:
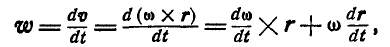
или
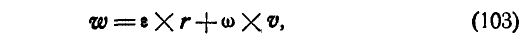
где
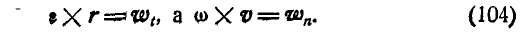
Действительно, в силу определения векторного произведения, находим:
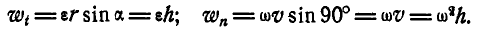
Это приводит нас к формулам (91). Направления же 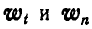 соответствуют правилу откладывания векторов, полученных по правилам векторного произведения (рис. 166).
соответствуют правилу откладывания векторов, полученных по правилам векторного произведения (рис. 166).
Задача №1
Маховик делает 360 об/мин. Найти его угловую скорость 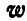 . ,
. ,
Решение. В нашем случае 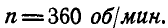 По формуле (94) находим:
По формуле (94) находим:
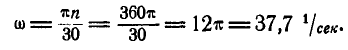
Задача №2
Маховик начинает вращаться равноускоренно из состояния покоя. Сделав с момента начала движения 60 оборотов, маховик имеет угловую скорость, равную 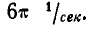 Определить угловое ускорение маховика.
Определить угловое ускорение маховика.
Решение. По условию задачи 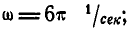
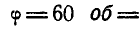
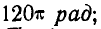
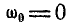 и
и 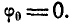
По формулам (99) получаем:
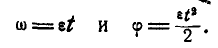
Подставляя значение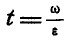 , найденное из первого уравнения, во второе, находим:
, найденное из первого уравнения, во второе, находим:
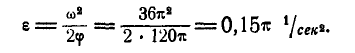
Задача №3
Тело делает 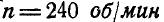 вокруг оси, составляющей углы
вокруг оси, составляющей углы 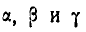 с координатными осями; при этом
с координатными осями; при этом 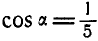 ,
, 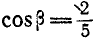 и
и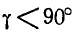 .
.
Найти такую точку тела, расположенную в плоскости 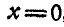 , проекции скорости которой суть:
, проекции скорости которой суть: 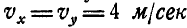 .
.
Решение. Угловая скорость:
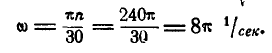
Для определения 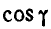 имеем известное соотношение:
имеем известное соотношение: 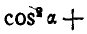
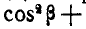
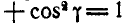 , откуда:
, откуда:
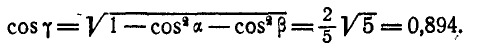
Найдем теперь проекции угловой скорости на координатные оси:
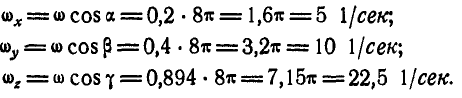
По формулам Эйлера (101) имеем:
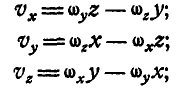
или
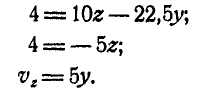
Из первых двух уравнений находим, что 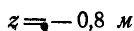 и
и 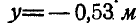 , а поэтому искомая точка будет:
, а поэтому искомая точка будет: 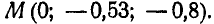
Задача №4
Маховик радиусом R = 1 м вращается вокруг неподвижной оси, проходящей через его центр перпендикулярно к плоскости чертежа, согласно уравнению 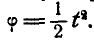
Найти скорость и ускорение точки М обода маховика по прошествии 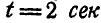 после начала его движения. Для всех точек маховика, расположенных вдоль радиуса ОМ, изобразить графически скорости и ускорения.
после начала его движения. Для всех точек маховика, расположенных вдоль радиуса ОМ, изобразить графически скорости и ускорения.
Решение. Найдем сначала по формулам (87) и (90) угловую скорость и угловое ускорение маховика:
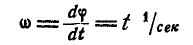
и
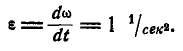
Далее, линейная скорость, нормальное и касательное ускорения’ точки М в момент t найдутся по формулам (89) и (91):
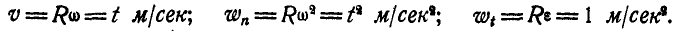
При 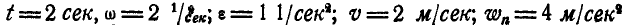 и
и 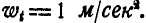
Величина и направление ускорения точки М определятся по формулам (92) и (93):
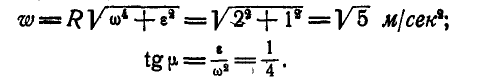
Так как величины линейных скоростей и ускорений точек, расположенных на одном из радиусов’маховика, например ОМ, зависят от величины самого радиуса, входящего в формулы (89) и (92) в первой степени, то отсюда следует, что концы векторов скоростей и ускорений точек одного радиуса будут расположены на прямой (рис. 167). Для удобства выполнения чертежа на радиусе ОМ дано изображение ускорений точек прямой ОМ, а на радиусе 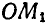 — изображение скоростей.
— изображение скоростей.
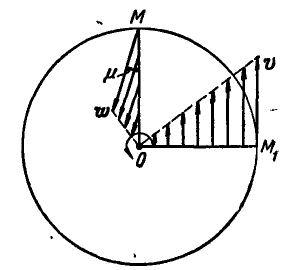
Рис. 167.
Задача №5
Диск, прикрепленный к вертикальной проволоке, совершает крутильные колебания вокруг оси проволоки так, что угол закручивания его меняется по закону: 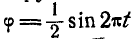 , где
, где 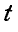 выражается в секундах.
выражается в секундах.
Найти нормальное, касательное и полное ускорения какой-либо точки М на ободе диска в момент 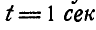 , если диаметр диска
, если диаметр диска 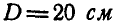 (рис. 168).
(рис. 168).
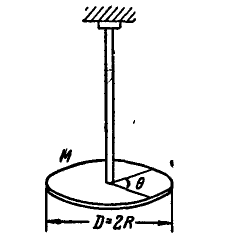
Рис. 168.
Указание: находим сначала угловую скорость и угловое ускорение диска по формулам (87) и (90), а затем ускорение точки М по формулам (91) и (92).
Ответ.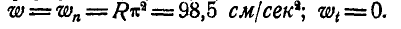
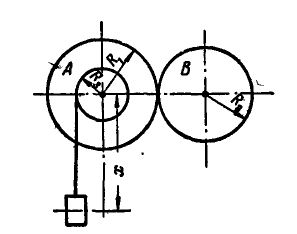
Рис. 169.
Задача №6
Зубчатое колесо А радиусом 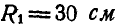 находится во внешнем зацеплении с колесом В радиусом
находится во внешнем зацеплении с колесом В радиусом 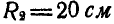 (рис. 169). На выступ радиусом
(рис. 169). На выступ радиусом 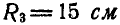 колеса А намотана нить, к концу которой подвешен груз. Движение груза в сантиметрах и секундах выражается уравнением:
колеса А намотана нить, к концу которой подвешен груз. Движение груза в сантиметрах и секундах выражается уравнением: 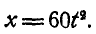 Найти угловую скорость и угловое ускорение колеса В, а также полное ускорение точки на ободе этого колеса.
Найти угловую скорость и угловое ускорение колеса В, а также полное ускорение точки на ободе этого колеса.
Решение. В общей точке касания колеса А и В имеют одинаковую линейную скорость, равную 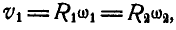 где
где 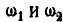 — угловые скорости колес А и В. Отсюда следует, что
— угловые скорости колес А и В. Отсюда следует, что 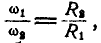
т. е. отношение угловых .скоростей колес обратно пропорционально их радиусам.
Найдем теперь угловую скорость 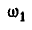 , и угловое ускорение
, и угловое ускорение 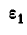 колеса А:
колеса А:
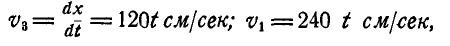
откуда
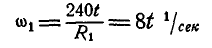
и
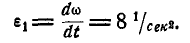
Вращение колес А и В равноускоренное, а поэтому 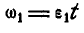 и
и 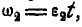 откуда
откуда
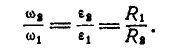
Отсюда угловая скорость 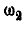 и угловое ускорение
и угловое ускорение 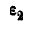 колеса В:
колеса В:
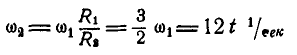
и
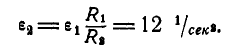
Ускорение какой-либо точки обода колеса В находим по формуле (92):
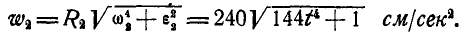
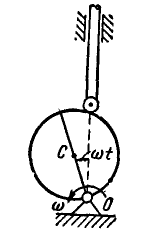
Рис. 170.
Вращение твердого тела вокруг неподвижной оси
Вращением вокруг неподвижной оси называют движение твердого тела, при котором его точки описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к их плоскостям
Вращательное движение
Как было показано, для определения движения твердого тела достаточно определить движение трех его точек, не лежащих на одной прямой. Пусть во- время движения тела две его точки О и O1 остаются неподвижными.
Тогда движение тела можно определить движением третьей точки К, принадлежащей телу и не лежащей на одной прямой с точками О и O1. Выберем эту точку произвольно и, соединив все три точки прямолинейными отрезками, получим треугольник OO1K-Так как точки О и O1 неподвижны, то неподвижна и сторона OO1 треугольника OO1K, и движение точки К, а также и всего тела определится поворотом плоскости треугольника OO1K вокруг прямой OO1. Точку К мы выбрали произвольно, следовательно, поворачивается вокруг прямой OO1 любая плоскость, проведенная в теле через эту прямую. Такое движение тела называют вращательным движением, или, коротко, вращением, а неподвижную прямую OO1, вокруг которой вращается тело, называют осью вращения.
Ось вращения может проходить и за пределами тела. Так, например, Луна, двигаясь вокруг Земли, повернута к ней всегда одной стороной. Движение Луны по отношению к Земле можно назвать вращением. Ось вращения проходит за пределами Луны через центры круговых траекторий ее точек.
Если движение тела определять по движению его точек, то вращение вокруг оси можно определить как движение твердого тела, при котором все точки тела описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к плоскостям этих окружностей, а ось вращения можно определить как неподвижную прямую, на которой расположены центры окружностей, описываемых точками вращающегося тела.
Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела: φ=φ(t)
Уравнение вращательного движения. Построим основную систему координат xcyz, направив ось Oz по оси вращения тела (рис. 101). Эта система неподвижная и не связана с вращающимся телом. Построим теперь другую, подвижную, систему координат x’0y’z’, направив ось Oz’ также по оси OO1 вращения тела, а ось Ox’ — на какую-либо точку K1 тела. Эта система координат неизменно связана с телом и поворачивается вместе с ним относительно основной системы xOyz. Угол φ на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела, называют углом поворота и обозначают буквой φ. Так, если в начальное мгновение оси Ox’ и Ox (см. рис. 101) совпадали, то углом поворота мы назовем двугранный угол между неподвижной плоскостью xθz и подвижной плоскостью x’Oz’ или равный ему линейный угол x’Ox’.
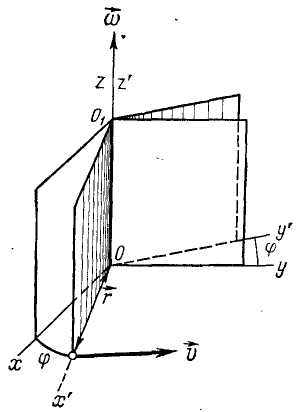
Рис. 101
Угол φ можно рассматривать как угловую координату тела, потому что он определяет положение всего вращающегося тела. Измеряется угол φ в радианах.
Будем считать угол φ положительным, если он отсчитан от положительной оси Ox к положительной оси Оу, т. е. против вращения часовой стрелки, если смотреть с положительного направления оси Oz. При отсчете в противоположную сторону будем считать угол отрицательном.
Чтобы определить вращение тела, надо знать угол поворота как некоторую непрерывную однозначную функцию времени:
φ=φ(t) (82)
Уравнение (82) является уравнением вращательного движения твердого тела вокруг неподвижной оси.
Всякая плоскость OO1K, проведенная через ось вращения и какую-либо точку К тела, поворачивается за данное время на такой же угол φ, на который за это же время повернулась плоскость x’Oz’. Это следует из условия неизменяемости твердого тела.
Угловая скорость выражается первой производной от угла поворота по времени:
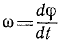
Угловая скорость. Угол поворота характеризует вращение тела только с геометрической стороны. Чтобы охарактеризовать вращение тела не только в пространстве, но и во времени, возьмем отношение изменения ∆φ угла поворота ко времени Δt, в течение которого это изменение происходило, называемое средней угловой скоростью тела:
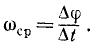 (83′)
(83′)
Пределом отношения (83′) при Δt, стремящимся к нулю, является первая производная от угла поворота по времени. Она характеризует изменение угла поворота в данное мгновение, т. е. характеризует вращение тела не только по отношению к окружающему пространству, но и во времени. Эта величина принята за пространственно-временную меру вращения твердого тела вокруг оси и ее называют угловой скоростью тела:
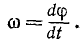 (83)
(83)
Знак производной (83) указывает, в какую сторону поворачивается тело вокруг оси Oz: если производная (83) положительна, то наблюдатель, смотрящий с положительной стороны оси Oz, видит тело вращающимся против часовой стрелки, т. е. справа налево — от положительного направления оси Ox к положительному направлению оси Оу: при отрицательной производной (83) вращение тела происходит в обратном направлении.
Размерность угловой скорости равна размерности угла поворота, деленной на размерность времени. Но угол поворота является отвлеченной величиной, и размерность его—единица. Следовательно, размерность угловой скорости обратна размерности времени.
[ω]=T-1.
Чаще всего время измеряют в секундах, тогда единица угловой скорости ceκ-1.
Равномерное вращение иногда характеризуют числом п оборотов, совершаемых телом за единицу времени (обычно за минуту).
Найдем соотношение между угловой скоростью ω, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает n оборотов в минуту, то оно поворачивается за каждую минуту на 2πn радианов, а за секунду—в 60 раз меньше, следовательно,
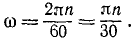 (84)
(84)
Формулу (84) широко применяют в технической механике. Приближенно можно считать
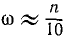 (84′)
(84′)
В формулах (84) и (84′) n выражеyо в оборотах за минуту, a ω — в радианах за секунду, как их большей частью и выражают. Однако для очень медленно вращающихся тел число оборотов удобнее считать не за минуту, а за другие единицы времени. Так, Земля вращается вокруг своей оси, делая 1 оборот в сутки. Было бы неудобно считать, что Земля делает 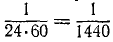 оборота в минуту. Угловую скорость Земли следует подсчитывать не по формуле (84), а из тех соображений, что Земля делает один оборот (2π радианов) за сутки, а в сутках 86400 сек, следовательно,
оборота в минуту. Угловую скорость Земли следует подсчитывать не по формуле (84), а из тех соображений, что Земля делает один оборот (2π радианов) за сутки, а в сутках 86400 сек, следовательно,
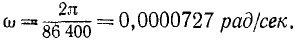
Самые медленные вращения встречаются в звездном мире. Так< например, период обращения Солнца вокруг центра Галактики (Млечного пути) составляет 190 миллионов лет.
Наибольшая угловая скорость, полученная в технике, соответствует миллионам оборотов в минуту. C такой скоростью вращаются гироскопы Гюгенара —маленькие роторы, подвешенные без подшипников в магнитном поле.
За одно и то же время все части твердого тела поворачиваются вокруг оси на один и тот же угол. Следовательно, угловая скорость является общей мерой вращения для всего тела, и в каждое мгновение тело, вращающееся вокруг оси, имеет только одну угловую скорость.
Для тех случаев, когда тело совершает сложное движение, например вращается вокруг оси в то время, как эта ось поворачивается, удобно изображать угловую скорость вектором, направленным вдоль оси вращения. Величина и положение вектора показывают величину угловой скорости и положение оси вращения. Но вектор угловой скорости, как и вектор момента силы относительно точки, отличается от прочих известных нашим читателям векторов (скорость точки, ускорение точки, радиус-вектор, сила и др.) тем, что, изображая его стрелкой соответствующей длины, отложенной вдоль оси вращения, надо (вполне произвольно) условиться относительно направления стрелки. В нашем курсе мы всюду пользуемся правой системой координат, поэтому установим и для вектора угловой скорости правило правого винта, т. е. будем направлять вектор угловой скорости вдоль оси вращения к той ее стороне, с которой вращение тела представляется происходящим против вращения часовой стрелки. Так, например, вектор угловой скорости земного шара, вращающегося с запада на восток, мы направим к северному полюсу: глядя с северного полюса, мы увидели бы Землю вращающейся против часовой стрелки.
Угловое ускорение выражается первой производной от угловой скорости по времени:
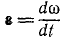
Угловое ускорение. Изменение угловой скорости происходит с течением Времени и, вообще говоря, бывает различным в разные моменты времени. Пространственно-временную меру, характеризующую изменение угловой скорости тела в данное мгновение, называют угловым ускорением тела.
Поскольку угловая скорость — векторная величина, вектором Должно быть и угловое ускорение. Но при вращении тела вокруг Неподвижной оси мы обычно рассматриваем угловую скорость как скаляр, и потому здесь нас могут интересовать только величина и знак углового ускорения.
Пусть величина угловой скорости изменилась на ∆ω в течение промежутка времени Δt. Предел отношения 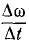 при Δt, стремящемся к нулю, выражает угловое ускорение тела и обозначается греческой буквой ε (эпсилон):
при Δt, стремящемся к нулю, выражает угловое ускорение тела и обозначается греческой буквой ε (эпсилон):
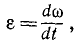 (85)
(85)
или, принимая во внимание равенство (83),
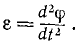
Следовательно, угловое ускорение выражается первой производной “от угловой скорости по времени, или, что то же, второй производной от угла поворота по времени. Эта величина характеризует быстроту изменения угловой скорости тела, вращающегося вокруг неподвижной оси.
Размерность углового ускорения равна размерности угла поворота, деленной на квадрат размерности времени, т. е. равна единице, деленной на квадрат времени.
[ω]=T-2.
Чаще всего время измеряется в секундах, тогда единица углового ускорения ceκ-2, или по записи, рекомендованной ГОСТом, pa∂/ceκ2.
Если с течением времени абсолютная величина угловой скорости тела увеличивается, то производная 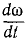 имеет тот же знак, что и ω, и вращение тела ускоренное. Если же величина угловой скорости с течением времени уменьшается, то производная
имеет тот же знак, что и ω, и вращение тела ускоренное. Если же величина угловой скорости с течением времени уменьшается, то производная 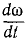 и угловая скорость имеют различные знаки — вращение тела замедленное. Каждое из этих вращений, и ускоренное и замедленное, называют переменным вращением.
и угловая скорость имеют различные знаки — вращение тела замедленное. Каждое из этих вращений, и ускоренное и замедленное, называют переменным вращением.
Задача №7
Унифиляр (тело, подвешенное на вертикальном стержне) (рис. 102) закрутили на угол 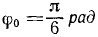 от равновесного положения и затем (в мгновение t = 0) предоставили самому себе, и он стал вращаться согласно уравнению
от равновесного положения и затем (в мгновение t = 0) предоставили самому себе, и он стал вращаться согласно уравнению
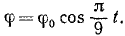
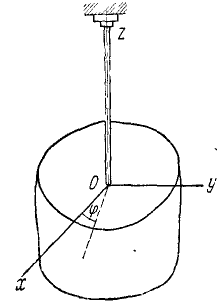
Рис. 102
Определить угловую скорость (в ρa∂/ceκ.) и угловое ускорение (в рад/сек) через каждые 3 сек от начала движения.
Решение. Дифференцируя уравнение движения, получим выражение угловой скорости унифиляра:
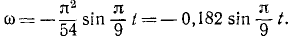
Дифференцируя вторично найдем, угловое ускорение унифиляра:
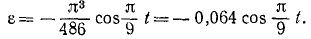
Чтобы определить угол поворота, угловую скорость и угловое ускорение в заданные мгновения, надо в уравнение движения тела и в полученные соотношения подставить t = 3, 6, 9, … и т. д. секунд. Анализируя полученные данные относительно ω и ε, убедимся, что унифиляр совершает крутильные колебания с периодом 18 сек.
- Заказать решение задач по теоретической механике
Равномерное и равнопеременное вращения
Если угловая скорость ω постоянна, то производная 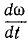 = 0, и вращение равномерное. Таким образом, при равномерном вращении тела угловое ускорение равно нулю, угловая скорость постоянна, а угол поворота изменяется пропорционально времени:
= 0, и вращение равномерное. Таким образом, при равномерном вращении тела угловое ускорение равно нулю, угловая скорость постоянна, а угол поворота изменяется пропорционально времени:
ε = 0, ω = const, φ = φ0+ωt, (86)
где φ0-начальное значение угла.
Формулы (86) справедливы только для равномерного вращения тела и неприменимы при других движениях.
Из различных переменных вращений тела в задачах наиболее часто встречается равнопеременное вращение. Равнопеременным вращением называют такое вращение твердого тела вокруг оси, πph котором угловое ускорение остается постоянным:
ε = const.
Интегрируя это уравнение, находим
ω = εt + C1.
Постоянную интегрирования C1 находим из начальных данных. В начальное мгновение (при t=0) величина угловой скорости была ω0. Подставляя эти частные значения аргумента t и функции ω, находим постоянную C1:
C1 = ω0.
Таким образом,
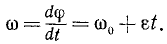
Интегрируя это равенство, получаем
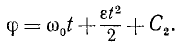
Постоянную C2 находим из начальных данных. Если при начале вращения тело было повернуто на некоторый угол φ0, то, подставляя φ0 вместо φ и 0 вместо t, найдем C2 = φ0. Для равнопеременного вращения тела имеем:
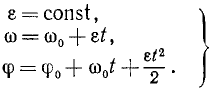 (87)
(87)
Формулы (87) справедливы только для равнопеременного вращения твердого тела и неприменимы при других движениях.
Задача №8
Барабан суперцентрифуги делает при установившемся движении 30000 об/мин, а после прекращения подачи энергии (на выбеге) вращается равнозамедленно с угловым ускорением ε=π1∕ceκ2. Определить время выбега (время до остановки) и угол поворота барабана за это время.
Решение. В мгновение прекращения подачи энергии угловая скорость барабана была
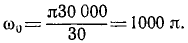
C этого мгновения барабан вращается равнозамедленно по (87):
ω= 1000π—πt.
В мгновение остановки барабана угловая скорость его равна нулю. Подставляя это значение угловой скорости, находим время выбега.
t = 1000 сек = 16 мин 40 сек.
За это время барабан повернется на угол
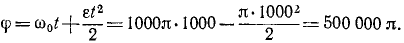
Чтобы по углу поворота определить число оборотов, надо поделить этот угол (выраженный в радианах) yа 2π—число радианов в одном обороте.
Ответ. t = 16 мин 40 сек, φ = 250 000 об.
Задача №9
В инерционном аккумуляторе Уфимцева (1918 г.) для ветроэлектрических станций стальной диск вращается в глубоком вакууме, делая 20 000 об/мин. Предоставленный самому себе, он продолжает вращаться в течение двух недель. Определить е диска, считая вращение равнозамедленным.
Решение. Определим начальную угловую скорость диска н время (2 нед.) до остановки в секундах:
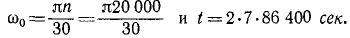
Ответ получим, разделив ω0 на t.
Ответ. 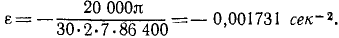
Траектории, скорости и ускорения точек вращающегося тела
Точки вращающегося тела, расположенные на одной прямой, параллельной оси вращения, совершают одинаковые движения
Траектории точек вращающегося тела
Вращением тела называют движение, при котором точки тела описывают окружности с центром на оси вращения. Следовательно, по самому определению вращательного движения траектории точек тела—окружности.
Если тело мысленно пересечь какой-либо плоскостью, перпендикулярной оси вращения, то в этой плоскости будут находиться круговые траектории всех расположенных в ней точек тела. Очевидно, что движения точек тела, лежащих на ном в какой-либо из точек к этой плоскости, совершенно одинаковы, а потому и движение точек всего тела может быть полностью охарактеризовано движением точек, лежащих в этой плоскости.
Сохраним и в этом параграфе расположение осей координат (см. рис. 101), при котором оси Oz и Oz’ неподвижной и подвижной систем совпадают с осью вращения тела, а плоскость x’0y’ находится в плоскости хОу.
Возьмем в этом теле какую-либо точку К (рис. 103), координаты которой относительно подвижной системы обозначимx’,y’ и г’. Эти координаты точки К во время вращения тела не меняются, так как оси подвижной системы координат неизменно связаны с телом и вращаются вместе с ним. Координаты той же точки в основной системе обозначим х, у и z.
Координаты х и у точки К связаны с координатами х’ и у’ той же точки формулами, известными из аналитической геометрии и понятными из чертежа (рис. 103):
х = х’ cos φ—y’ sin φ, (88′)
y = x’ sin φ +y’ os φ. (88″)
Если тело вращается, то с течением времени меняется угол φ, являющийся некоторой функцией (71) от времени t, а следовательно, меняются и координаты х и у точки К в основной системе отсчета. Координата же z при направлении оси Oz вдоль оси вращения не изменяется и остается равной z’:
z = z’. (88″‘)
Аналогично можно определить подвижные координаты по неподвижным и углу φ:
х’ = х cos φ у sin φ; y’ = y cos φ—x sinφ; z’ = z.
Скорость точки тела, вращающегося вокруг оси, равна произведению угловой скорости тела на расстояние точки от оси: υ= ωr
Скорости точек вращающегося тела. Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (88), рассматривая φ как функцию времени. Будем иметь
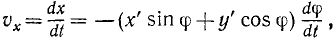
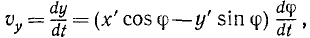
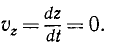
Но согласно (88) выражение, стоящее в скобках в первом из этих равенств, есть у, а во втором х, а потому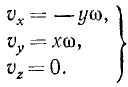 (89)
(89)
Возводя эти равенства в квадрат и складывая, найдем
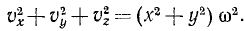
Но в левой части мы имеем квадрат полной скорости точки, а в скобках правой части — квадрат расстояния точки от оси. Мы получили одну из главнейших формул кинематики:
υ = ωr (90)
— величина скорости точки вращающегося тела равна произведению угловой скорости тела на расстояние точки от оси вращения.
Таким образом, для определения скорости точки вращающегося тела нет необходимости знать ее координаты, надо знать лишь расстояние точки от оси вращения и угловую скорость тела.
Можно определить угловую скорость тела по скорости какой-либо из его точек и по расстоянию этой точки от оси вращения:
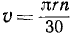 (91)
(91)
По этим формулам можно определить скорость любой точки вращающегося тела, независимо от того, какую форму имеет тело и находится точка на поверхности или внутри тела. Скорость точки тела, вращающегося вокруг оси, называют вращательной скоростью точки. Она направлена перпендикулярно к плоскости, проходящей через точку и ось вращения, против хода часовой стрелки или по ходу часовой стрелки в зависимости от знака производной (83).
Если же смотреть на тело с той стороны оси вращения, куда мы направили вектор 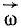 угловой скорости, то вектор вращательной скорости
угловой скорости, то вектор вращательной скорости 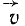 всякой точки тела направлен против хода часов. Такое же направление (против хода часов) имеет вектор
всякой точки тела направлен против хода часов. Такое же направление (против хода часов) имеет вектор 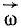 , если смотреть на него с конца вектора вращательной скорости
, если смотреть на него с конца вектора вращательной скорости 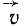 .
.
Следовательно, вектор вращательной скорости точки и по величине и по направлению можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Его можно представить в виде векторного произведения аналогично тому, как это сделано в статике с моментом силы относительно точки.
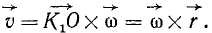
Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т. п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ω на радиус R тела:
υoκp = ωR.
Задача №10
Определить вращательную скорость точек земной поверхности на экваторе и на широте Москвы (55°45′) при вращении Земли вокруг оси (рис. 104). Средний радиус Земли 6371 км и cos 55o45′ = 0,5628.
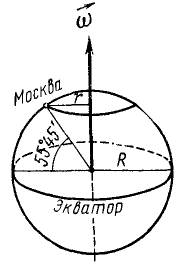
Рис. 104
Решение. Вращаясь вокруг своей оси, Земля совершает один оборот (2π рад) за сутки (86 400 сек), и угловая скорость Земли ω=727∙10-7 pa∂/ceκ. Умножая угловую скорость на радиус Земли, выраженный в метрах (6371 ∙ 103), найдем вращательную скорость точек Земли на экваторе:
υ= ωR=727 • 6371 • 10-4 = 463 м/сек.
Для определения вращательной скорости точек в Москве надо умножить ω Земли на расстояние г от Москвы до земной оси:
υ = 727 • 10-7 • 0,5628 • 6371 • 103 = 261 м/сек.
Ответ. Вращательная скорость точек на экваторе 463 м/сек, в Москве 261 м/сек.
Она направлена против вращения часовой стрелки, если смотреть с северного полюса.
Задача №11
Шкив динамомашины R1= 15 см (рис. 105) вращается посредством бесконечного ремня от паровой машины со шкивом R2 — 60 см, делающим 100 об/мин. Определить угловую скорость ω1 шкива динамомашины.
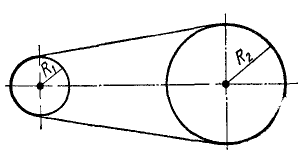
Рис. 105
Решение. Определим окружную скорость шкива паровой машины:
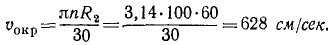
Такова же величина скорости частиц ремня, а следовательно, и окружная скорость шкива динамомашины. Его угловая скорость
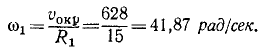
Ответ. ω1=41,87 рад/сек, n = 400 об/мин.
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения тела: αr=er
Ускорение точек вращающегося тела
Если в выражении касательного (69) и нормального (74) ускорений вместо скорости v мы подставим выражение (90) вращательной скорости, то получим касательное и нормальное ускорения точки тела, вращающегося вокруг неподвижной оси.
Касательное ускорение
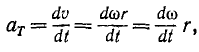
или
aτ = εr. (92)
Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения.
Центростремительное ускорение точки вращающегося тела равно произведению квадрата угловой скорости тела на расстояние точки от оси вращения тела:
αN=ω2r
Каждая точка вращающегося тела описывает окружность, а потому радиус кривизны р траектории точки равен расстоянию этой точки от оси вращения тела. Имеем
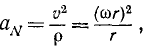
или
αN=ω2r
Нормальное ускорение точки вращающегося тела обычно называют центростремительным ускорением. Оно равно произведению квадрата угловой скорости на расстояние точки от оси вращения тела.
Величина полного ускорения точки тела, вращающегося вокруг оси, выражается формулой
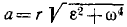
Зная касательное и центростремительное ускорения, определим по формуле (75) величину полного ускорения этой точки:
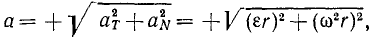
или
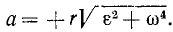 . (94)
. (94)
Иногда бывает необходимо определить проекции ускорения точки вращающегося тела на неподвижные оси координат. Для этого продифференцируем равенства (89) по времени, учитывая, что при вращении тела меняется не только его угловая скорость, но и координаты х и у его точек:
ax =—уε—υyω, ay = xε+υλω, αz = 0.
Подставляя вместо υx и υy их значения (89), найдем проекции ускорения точки вращающегося тела на неподвижные оси:
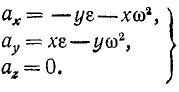 . (95)
. (95)
Возводя в квадрат и складывая, найдем
a2 = (x2 + y2) (ε2 + ω4),
или, так как x2+y2 = r2, получаем уже знакомую нам формулу (94). Следовательно,
aTх=—yε; αTy = xε; aNх= — xω2; aNy=-yω2. (95′)
Задача №12
Тело вращается вокруг оси Oz без начальной угловой скорости и с постоянным угловым ускорением ε = 0,4 рад/сек2. Определить для t = 10 сек: 1) координаты точки К тела, если при t = 0 координаты точки К были: х = +10, y=0, z-0∙, 2) ее вращательную скорость; 3) направляющие косинусы вращательной скорости; 4) касательное и центростремительное ускорения той же точки; 5) направляющие косинусы касательного и центростремительного ускорений; 6) угол, составляемый векторами полного и центростремительного ускорений.
Решение. Тело вращается равноускоренно; по (87) найдем угловое ускорение, угловую скорость и угол поборота тела для заданного мгновения: ε = 0,4 ρaд/ceκ2; ω = 0,4 • 10 = 4 ρaд/ceκ;
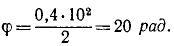
Тело повернулось за 10 сек на 20 рад. Переведем радианы в градусы:
ar = 1145о54’56”,
за вычетом полных оборотов определим угол αr, составляемый радиусом-вектором с осью Ox (рис. 106):
20 рад = 65о54’56”,
По тригонометрическим таблицам находим: cos ar = 0,4080, sin ar = 0,9130. Приняв во внимание, что расстояние точки К от оси вращения тела равно 10 см, найдем координаты точки К в мгновение t=10 сек:
х=10 cos ar = +4,080 см,
y = 10 sin ar = +9,130 см.
Величину вращательной скорости определим по (90):
υ = ωr = 4 • 10 = 40 см/ceκ.
Чтобы определить направляющие косинусы вращательной скорости, найдем сначала по (89) ее проекции на оси координат:
υx= — yω = — 36,52 см/сек,
υy= +xω = + 16,32 см/сек
по затем по (62) — направляющие косинусы:
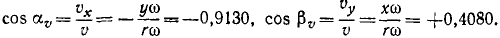
Определим по (92) величину касательного ускорения:
aτ=εr = 0,4 ∙10 = 4 см/ceκ2
и по (95′) — проекции касательного ускорения на оси х и у:
aTx = — yε=—3,652 см/сек2, aTy = xε =+1,632 см/сек2.
Разделив проекции на модуль касательного ускорения, найдем направляющие косинусы касательного ускорения:
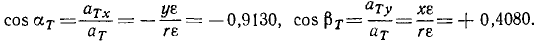
Мы видим, что направляющие косинусы касательного ускорения тождественны с направляющими косинусами скорости.
Напомним, что знак направляющего косинуса определяется знаком числителя. Если ω и ε имеют одинаковые знаки (как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки ω и ε различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны.
Величину центростремительного ускорения определим по (93);
aN=ω2r = 42∙10 = 160 см/сек2
и по (95′) —его проекции на оси координат:
aNx=—xω2= —65,280 см/сек2,
aNy = — yω2 = —146,080 см/сек2.
Проекции нормального ускорения точки на оси координат имеют знаки, обратные знаку соответствующей координаты точки. В самом деле, ayx отрицательна, если абсцисса х положительна, и положительна, если х отрицательна (аналогично и ayy). Следовательно, центростремительное ускорение всегда направлено к началу координат, т. е. к центру круговой траектории точки.
Разделив проекции центростремительного ускорения на его модуль, найдем направляющие косинусы центростремительного ускорения:
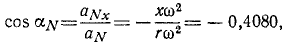
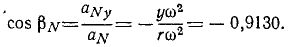
Так как касательное ускорение перпендикулярно к центростремительному, то (по условию перпендикулярности, известному из аналитической геометрии) сумма произведений соответствующих направляющих косинусов должна равняться нулю. Действительно,
cos aT cos aN + cos βT cos βN = ( — 0,9130) ( —0,4080) + ( + 0,4080) ( — 0,9130) =0.
Определим теперь тангенс угла между направлением полного и нормального ускорений:
Пользуясь таблицами тригонометрических функций, определим, что угол равен lo26’0″.
Ответ. 1) х = + 4,080 см, у = + 9,130 см; 2) υ = 40 см/сек, 3)cos aυ=—0,9130, cos βυ = +0.4080; 4) aT = 4 см/сек1, aN= 160 см/сек2; 5) cos aT=—0,9130, cos βT= +0,4080, cos aN = – 0,4080, cos βN=—0,9130; 6) угол равен lo26’0″.
Задача №13
При сборке ротора молотковой дробилки была допущена неточность, в результате которой центр тяжести ротора отстоит от оси вращения на расстоянии 1 мм. Определить центростремительное ускорение центра тяжести ротора, если n = 3000 об/мин.
Решение. По формулам (84) и (93) имеем
Ответ. aN=98,6 м/сек2 ≈ 10g.
Зависимости между углом поворота, угловой скоростью, угловым ускорением и временем аналогичны зависимостям между расстоянием, скоростью, касательным ускорением и временем
Аналогия формул
Формулы кинематики вращательного движения аналогичны соответствующим формулам кинематики точки и могут быть из них получены, если заменить расстояние s углом поворота φ, скорость υ— угловой скоростью ω и касательное ускорение αT-угловым ускорением ε. Это правило является мнемоническим, оно непригодно для вывода формул, но может облегчить их запоминание. Ниже приведен ряд формул, получающихся одна из другой такой заменой.
| Движение точки | Вращение точки |
|
Уравнение движения по траектории Средняя скорость точки Величина скорости точки Величина касательного ускорения Равномерное движение точки Равнопеременное движение |
Уравнение вращения вокруг оси Средняя угловая скорость тела Величина угловой скорости тела Величина углового ускорения Равномерное вращение тела Равнопеременное вращение |
- Сферическое движение твердого тела
- Плоско-параллельное движение твердого тела
- Движение твердого тела, имеющего неподвижную точку
- Движение твердого тела
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
[/spoiler]
Содержание:
- Кинематика твердого тела
- Простейшие движения твердого тела
- Поступательное движение твердого тела
- Вращательное движение твердого тела вокруг неподвижной оси
- Закон вращательного движения
- Угловая скорость и угловое ускорение вращающегося тела
- Угловая скорость
- Угловое ускорение
- Некоторые случаи вращения тела вокруг неподвижной оси
- Равномерное вращение
- Равномерно переменное вращательное движение
- Кинематические характеристики точек тела, вращающегося вокруг неподвижной оси
- Линейная скорость
- Линейное ускорение
- Векторы угловой скорости и углового ускорения вращающегося тела
- Векторное выражение линейной скорости точки тела, вращающегося вокруг неподвижной оси
- Векторное выражение нормального и тангенциального ускорений
- Передача вращательного движения
Кинематика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Кинематика твердого тела
В кинематике твердого тела определяются закон движения и кинематические характеристики абсолютно твердого тела, а также кинематические характеристики точек тела.
Абсолютно твердым телом называется материальное тело, в котором расстояния между любыми двумя его точками остается постоянным.
Простейшие движения твердого тела
После рассмотрения кинематики материальной точки перейдем к изучению движения твердого тела. Рассмотрим сначала его простейшие виды — поступательное и вращательное.
Поступательное движение твердого тела
Поступательным называется такое движение твердого тела, при котором произвольная прямая, проведенная на этом теле, перемещается, всегда оставаясь параллельной самой себе.
Примерами поступательного движения твердого тела может быть: движение планки мотовила зерноуборочного комбайна при прямолинейном его движении; движение клавиши соломотряса (шарнирного параллелограмма O1ABO2 рис. 2.10, а), который осуществляет круговое поступательное движение; поступательное движение штанги кулачкового механизма (рис. 2.10, б), которой осуществляет обратнопоступательное движение; движение педали велосипеда относительно рамы, поршня двигателя
относительно цилиндра, движение кузова автомобиля при прямолинейном движении и т. п.
Таким образом, траектории движения точек тела при поступательном движении могут быть как прямая линия, так и любые кривые. Термин “поступательное движение” касается только тела, а не точки.
Каким же образом определяются кинематические характеристики движения твердого тела при поступательном движении? Рассмотрим теорему
“При поступательном движении тела все его точки движутся по тождественных траекториях и имеют в каждый момент времени одинаковые скорости и ускорения”.

Доказательство: Пусть есть тело, которое движется поступательно и которое за некоторый промежуток времени перешло из одного положения в другое (рис. 2.11). Прямая AB, проведена через произвольные точки А и В тела осталась параллельной
самой себе и заняла новое положение A´B´. Выберем за начало отсчета произвольную точку О. Проведем из точки О радиусы — векторы  ,
,  двух произвольных точек тела А и В. Из треугольника ОАВ, что создано на рис. 2.11, следует, что
двух произвольных точек тела А и В. Из треугольника ОАВ, что создано на рис. 2.11, следует, что

Согласно определению поступательного движения тела вектор  , соединяющий
, соединяющий
точки А и В и перемещается параллельно самому себе является постоянным вектором,
потому что точки А и В принадлежат твердому телу:

То есть, при поступательном движении тела радиусы — векторы  и
и  произвольных точек А и В, изменяясь по направлению, будут отличаться согласно формуле на один и тот же постоянный вектор
произвольных точек А и В, изменяясь по направлению, будут отличаться согласно формуле на один и тот же постоянный вектор  .
.
Итак, из этого следует, что траекторию движения точки В можно получить, сместив траекторию точки А по направлению вектора  на расстояние AB, и поэтому эти траектории будут тождественными, конгруэнтными (совмещаются при наложении).
на расстояние AB, и поэтому эти траектории будут тождественными, конгруэнтными (совмещаются при наложении).
Определим скорости точек A и B тела. Для этого продифференцируем по времени выражение:

Вторая составляющая правой части этого выражения будет равна нулю:

поскольку  = const, то окончательно имеем:
= const, то окончательно имеем:

а это скорости точек А и В:
 =
=  .
.
Таким образом, скорости точек А и В движущегося тела постепенно, равны по величине и имеют одинаковое направление, поскольку они расположены на касательных к одинаковым траекториям движения и направлены в одну и ту же сторону.
Определим ускорение точек А и В. После второго дифференцирования по времени выражения имеем:

Как и в предыдущем случае имеем  поскольку
поскольку  = const. Тогда окончательно:
= const. Тогда окончательно:

или

и
 =
=  .
.
Таким образом, поступательное движение тела вполне определяется движением
какой-либо одной его точки.
Окончательно можно сделать следующие вывод: определение поступательного
движения твердого тела сводится к определению движения только одной его точки,
поскольку все точки тела движутся одинаково. При этом скорость и ускорения, которые являются общими для всех точек тела, называются скоростью и ускорением поступательного движения тела, а уравнения движения любой его точки является уравнением поступательного движения тела.
Таким образом, в результате полного тождества движения всех точек тела, движется поступательно, большинство задач по кинематике такого движения тела решается методами кинематики материальной точки.
Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение вокруг неподвижной оси – это движение твердого тела, при котором все его точки, двигаясь в параллельных плоскостях, описывают окружности с центрами, лежащими на одной неподвижной прямой, называемой осью вращения.
Закон вращательного движения
Кроме поступательного движения твердого тела в простых относится вращательное движение. Вращательное движение тел наиболее распространено используется в технике. Рассмотрим его сущность и сначала сформулируем его определение.
Вращательным движением твердого тела называется такое движение, при котором все точки тела движутся по кругам, центры которых лежат на одной прямой, которая называется осью вращения.
Ось вращения может находиться, как внутри самого тела, так и быть снаружи его.
Для того, чтобы осуществить вращательное движение твердого тела, необходимо закрепить неподвижно две любые точки этого тела, например, в подшипниках, тогда прямая, проходящая через все точки будет осью вращения и будет оставаться при вращении тела неподвижной.
Определим положение тела, вращающегося вокруг неподвижной оси.
Представим твердое тело, вращающееся вокруг неподвижной оси z (рис. 2.12).
Проведем через ось вращения z две полуплоскости, одна из которых  есть
есть
неподвижной полуплоскостью, а вторая полуплоскость  неизменно сопряжена с
неизменно сопряжена с
телом и вращается вместе с ним. Тогда положение тела в любой момент времени t однозначно определяется двугранным углом φ между полуплоскостями  и
и  , взятыми с соответствующим знаком, называется углом поворота тела φ.
, взятыми с соответствующим знаком, называется углом поворота тела φ.
При вращении тела вокруг неподвижной оси z угол поворота φ является непрерывной и однозначной функцией времени:
φ = φ(t).

Выражение называется законом вращательного движения тела или кинематическим уравнением вращательного движения.
Если есть эта функция, то положение тела будет полностью определено. То есть каждому значению параметра времени t имеем в соответствии только единую величину угла φ.
Угол поворота φ тела вокруг неподвижной оси имеет знак. Так, угол φ будет
положительным (φ > 0), если смотреть с положительного конца оси z видеть вращения
подвижной плоскости  в направлении против часовой стрелки. И наоборот, будет отрицательным (φ < 0), когда глядя с положительного конца оси z, видеть вращения подвижной плоскости
в направлении против часовой стрелки. И наоборот, будет отрицательным (φ < 0), когда глядя с положительного конца оси z, видеть вращения подвижной плоскости  по направлению движения часовой стрелки.
по направлению движения часовой стрелки.
Угол поворота тела измеряется в радианах или оборотах. Как известно, один оборот равен 2π рад. Поэтому связь между углом поворота φ, что измеряется в радианах, и углом поворота N, измеряется в оборотах, будет таким:
φ = 2πN,
где N — количество оборотов тела.
Угловая скорость и угловое ускорение вращающегося тела
Кинематическими характеристиками вращательного движения твердого тела является
угловая скорость ω и угловое ускорение ε.
Определим эти кинематические характеристики.
Угловая скорость
Угловая скорость ω характеризует изменение угла поворота тела φ за единицу времени, или показывает, как быстро тело вращается.
Если за некоторый промежуток времени ∆t = t1 – t тело совершает поворот на угол ∆φ = φ1 – φ, то средняя угловая скорость ωc тела за этот промежуток времени будет равна такому отношению:

Для нахождения угловой скорости ω тела в любой момент времени t необходимо ωc представить в виде границы, к которой приближается его значение, когда промежуток времени ∆t стремится к нулю:

Таким образом, угловая скорость тела в любой момент времени равна первой производной от угла поворота по времени.
Знак ω определяет направление вращения тела и, в свою очередь, определяется знаком угла поворота φ. Если ω > 0 , то тело в данный момент времени вращается в положительном направлении, и, наоборот, если ω < 0 , то тело вращается в отрицательном направлении.
Единица измерения угловой скорости ω: 
Угловое ускорение
Угловое ускорение ε тела, вращающегося вокруг неподвижной оси характеризует изменение угловой скорости ω за единицу времени.
Если за промежуток времени ∆t = t1 – t угловая скорость меняется на величину ∆ω = ω1 – ω, то среднее угловое ускорение εc тела за этот промежуток времени будет численно равно:

Для нахождения углового ускорения ε тела в любой момент времени t необходимо εc представить в виде границы, к которой приближается его значение, когда промежуток времени ∆t стремится к нулю:

или

Таким образом, угловое ускорение тела в любой момент времени численно равно первой производной от угловой скорости или второй производной от угла поворота по времени.
Единица измерения углового ускорения ε: 
Из выше изложенного следует, что если модуль угловой скорости ω с временем растет (ε > 0), то вращение тела будет ускоренным, а если уменьшается (ε < 0), то вращательное движение будет замедленным.
Следует также заметить, что вращение тела вокруг оси будет ускоренным, если знаки перед угловой скоростью ω и угловым ускорением ε будут одинаковыми, и наоборот — замедленным, если знаки перед указанными величинами будут разными.
Некоторые случаи вращения тела вокруг неподвижной оси
В зависимости от того, какие кинематические характеристики имеет тело при
вращении вокруг неподвижной оси, возможны некоторые случаи. Рассмотрим их.
Равномерное вращение
Если угловая скорость тела остается за все время движения тела постоянной, то вращение называется равномерным. При таком движении угловая скорость ω = const, а ε = 0. Угол поворота тела можно определять по следующей формуле
φ = ω · t,
или угловая скорость будет равна

В технике скорость равномерного вращения тел чаще всего определяют частотой вращения n, которая измеряется в 
Установим связь между указанными кинематическими характеристиками. Так, известно, что при одном обороте тело вернется на угол 2π, а при n оборотах — на угол 2πn. Теперь, если этот поворот (на угол 2πn) происходит за одну минуту, или 60 сек, то связь между угловой скоростью ω вращения тела и частотой n его вращения выражается следующей зависимостью:

Равномерно переменное вращательное движение
В таком случае вращения тела вокруг неподвижной оси угловое ускорение ε = const, то есть угловая скорость тела ω за равные промежутки времени меняется на одну и ту же величину.
Определим кинематические характеристики равномерно переменного вращательного движения. Поскольку ε = const, а согласно формуле ε =  , то отсюда есть возможность
, то отсюда есть возможность
определить угловую скорость движения тела. Она равна:
dω = ε · dt.
Угловая скорость ω находится под знаком дифференциала, а потому для ее нахождения необходимо взять интегралы от левой и правой частей выражения. Используем для этого определенные интегралы, для которых задаем верхнюю и нижнюю границы изменения переменных величин:

После интегрирования получим
ω – ω0 = εt ,
или
ω = ω0 + εt ,
где ω0 — начальная угловая скорость тела.
Далее используем выражение, согласно которому ω =  . Имеем возможность с него определить угол φ. Он будет равняться
. Имеем возможность с него определить угол φ. Он будет равняться
dφ = ω · dt .
Вместо ω подставим в выражение его значение:
dφ = ω0 + εt · dt.
Как и в предыдущем случае, найдем угол поворота тела φ, взяв определенные интегралы от левой и правой частей выражения. также задаем верхние и нижние границы изменения величин. Будем иметь:

После интегрирования получим:
φ – φ0 = ω0t + ε 
Окончательно получим:
φ = φ0 + ω0t + 
где φ0 — начальный угол поворота тела.
Таким образом, при равнопеременном вращательном движении твердого тела угловая скорость ω и угол поворота φ определяются с помощью формул. Следует заметить, что знаки в правых частях этих формул (перед ε) показывают характер равнопеременного вращательного движения. Так, если они положительные, то движение есть равноускоренным, а если отрицательные, то раавнозамедленным.
Пример:
Приводной вал комбайна начинает вращаться из состояния покоя с угловым ускорением ε = 7,5 рад/с2. Определить угловую скорость вала в конце 15 секунды. Определить также, сколько оборотов сделает вал за эти 15 секунд.
Решение.
По условию примера угловое ускорение вала есть постоянная положительная
величина, а потому его вращательное движение будет равноускоренным. Для
определения угловой скорости ω и угла поворота φ вала можно воспользоваться выражениями соответственно, используемые при рассмотрении равноускоренного движения:

Следует сразу заметить, что, поскольку вал начинает вращаться из состояния покоя, то его начальная угловая скорость равна нулю. Начальный угол поворота равен нулю, поскольку совмещаем начало отсчета угла поворота с началом движения. То есть:
ω0 = 0,
φo = o
Подставим дальше в выражение для угловой скорости значение углового ускорения ε и времени t1 = 15 c. Тогда угловая скорость ω после пятнадцатой секунды будет равна:

Подставим в выражение для угла поворота φ вала известные величины, получаем его значение за 15 секунд:

Для нахождения общего числа оборотов вала воспользуемся таким выражением:
φ = N · 2π.
Отсюда число оборотов N вала за 15 с равно:

Кинематические характеристики точек тела, вращающегося вокруг неподвижной оси
Кроме общих кинематических характеристик вращающегося тела вокруг неподвижной оси — угловой скорости ω и углового ускорения ε — рассмотрим кинематические характеристики отдельных точек вращающегося тела. К этим характеристикам относятся линейные или круговые скорости точек и линейные или круговые ускорения точек тела.
Линейная скорость
Рассмотрим тело, вращающееся вокруг неподвижной оси z (рис. 2.13). Направление вращения показано стрелкой. Выберем в теле любую точку M, которая размещается на расстоянии R от оси вращения z. при вращении тела точка M описывает окружность радиуса R, плоскость которого перпендикулярна оси z вращения, а центр C расположен на самой оси z.
За некоторый промежуток времени dt происходит элементарный поворот тела на угол dφ, при этом точка M осуществит вдоль своей траектории перемещение в положение M1 на такую величину:
dS = Rdφ.
Определим линейную скорость точки M. По известному выражению она будет равняться

то есть
 = ωR.
= ωR.

Эта скорость носит название линейной или круговой скорости точки, принадлежит телу, которое вращается вокруг неподвижной оси.
Таким образом, линейная скорость точки твердого тела, вращается вокруг неподвижной оси, численно равна произведению угловой скорости тела на радиус вращения (расстояние от данной точки до оси вращения).
Направление вектора линейной скорости  — по касательной
— по касательной  в круг (перпендикулярно радиусу вращения), которое описывается точкой М во время движения и всегда направлено в сторону вращения.
в круг (перпендикулярно радиусу вращения), которое описывается точкой М во время движения и всегда направлено в сторону вращения.
Поскольку для всех точек тела угловая скорость ω в данный момент времени имеет одно и то же значение, то линейные скорости точек тела, которое вращается, пропорциональные их расстояниям до оси вращения.
Если есть тело, вращающееся вокруг оси, перпендикулярной плоскости рисунка, то для диаметра KL будет иметь место эпюра распределения скоростей точек, которая имеет линейный характер (рис. 2.14).

Линейное ускорение
Определим далее ускорение точки М, принадлежащее телу, которое вращается вокруг неподвижной оси (см. рис. 2.14). Для этого можно воспользоваться полученными ранее уравнениями, а именно:

где

В данном случае ρ = R, тогда, подставляя значения, будем иметь значение крутящего, касательного ускорения

и центростремительного, нормального ускорения

Направления векторов полученных составляющих ускорений будут направлены так. Касательное ускорение  всегда направлено по касательной к траектории движения точки M, то есть перпендикулярно радиусу R. Причем, если вращение тела будет ускоренным, то направление
всегда направлено по касательной к траектории движения точки M, то есть перпендикулярно радиусу R. Причем, если вращение тела будет ускоренным, то направление  будет в сторону вектора скорости
будет в сторону вектора скорости  , если замедленное — то против. Нормальное ускорение
, если замедленное — то против. Нормальное ускорение  всегда положительное и его вектор направлен к центру окружности, по которой движется точка M.
всегда положительное и его вектор направлен к центру окружности, по которой движется точка M.
Определим полное ускорение a точки M. Оно будет равняться геометрической сумме составляющих касательного a и нормального an ускорений. По модулю это ускорение равно:
и нормального an ускорений. По модулю это ускорение равно:

или

Определим направление вектора полного ускорения  , для этого рассмотрим движение материальной точки M по кругу с угловой скоростью ω и угловым ускорением ε, что осуществляется в плоскости рисунка, направления которых показаны на рис. 2.15. Покажем направления векторов касательного
, для этого рассмотрим движение материальной точки M по кругу с угловой скоростью ω и угловым ускорением ε, что осуществляется в плоскости рисунка, направления которых показаны на рис. 2.15. Покажем направления векторов касательного  , нормального
, нормального  и полного
и полного  ускорений. Тогда отклонения вектора полного ускорения
ускорений. Тогда отклонения вектора полного ускорения  от нормали n к траектории движения точки определяется углом φ, который может быть вычислен по такому выражению:
от нормали n к траектории движения точки определяется углом φ, который может быть вычислен по такому выражению:

Следует заметить, что поскольку угловая скорость ω и угловое ускорение ε имеют в данный момент времени для всего тела одно и то же значение, то из выражений для полного ускорения  и для угла отклонение φ следует, что ускорение всех точек вращающегося тела вокруг неподвижной оси, пропорциональные их расстояниям от оси вращения и образуют одинаковый угол φ с радиусами кругов, описывающих различные точки тела, который равен
и для угла отклонение φ следует, что ускорение всех точек вращающегося тела вокруг неподвижной оси, пропорциональные их расстояниям от оси вращения и образуют одинаковый угол φ с радиусами кругов, описывающих различные точки тела, который равен

не зависит от радиуса и в данный момент одинаков для всех точек тела.
Безусловно, что линейные скорости и линейные ускорения точек, расположены на оси вращения, равны нулю.

Векторы угловой скорости и углового ускорения вращающегося тела
Угловую скорость ω вращающегося тела можно представить как вектор.
Вектор угловой скорости вращающегося тела расположен на оси вращения и направлен так, что, смотря на него с конца, можно видеть вращения тела против направления движения часовой стрелки.
Это так называемое “правило буравчика”.
Угловое ускорение ε вращающегося тела можно представить как вектор.
Вектор углового ускорения вращающегося тела расположен на оси вращения и направлен в ту же сторону, что и вектор угловой скорости если вращение ускоренное, и в направлении, которое противоположно направлению вектора угловой скорости, если вращение замедлено.
Если рассматривать различные случаи вращения твердого тела вокруг неподвижной оси и разное их использование, то направления векторов  и
и  будут такими, как показано на (рис. 2.16).
будут такими, как показано на (рис. 2.16).

Как видим, могут быть два варианта, когда векторы угловой скорости  и
и  направлены в одну сторону (рис. 2.16 а), или указанные векторы, которые направленные в разные стороны (рис. 2.16 б). Направления вращения тела показаны стрелками.
направлены в одну сторону (рис. 2.16 а), или указанные векторы, которые направленные в разные стороны (рис. 2.16 б). Направления вращения тела показаны стрелками.
Векторы угловой скорости  и углового ускорения
и углового ускорения  являются векторами скользящими, а это значит, что за их начало можно взять любые точки тела, расположенные на оси оборота.
являются векторами скользящими, а это значит, что за их начало можно взять любые точки тела, расположенные на оси оборота.
Задание векторов  и
и  полностью характеризует и определяет вращательное движение тела, направление вращения, а также численные значения угловой скорости и углового ускорения, учитывая длину векторов и масштабные коэффициенты.
полностью характеризует и определяет вращательное движение тела, направление вращения, а также численные значения угловой скорости и углового ускорения, учитывая длину векторов и масштабные коэффициенты.
Векторное выражение линейной скорости точки тела, вращающегося вокруг неподвижной оси
Линейную скорость точки вращающегося тела можно представить в виде векторного произведения. Докажем это.
Представляем тело, вращающееся вокруг неподвижной оси z в направлении, что показано стрелкой (рис. 2.17). Возьмем в теле произвольную точку M и покажем траекторию ее движения и радиус R. Покажем далее на оси вращения z с любой произвольной точки O вектор угловой скорости  и с этой же точки проведем радиус — вектор
и с этой же точки проведем радиус — вектор  , который определяет положение данной точки M тела.
, который определяет положение данной точки M тела.
Общеизвестно, что векторным произведением двух векторов  и
и  , угол между которыми составляет α есть третий вектор
, угол между которыми составляет α есть третий вектор  (
( =
=  х
х  ), модуль которого равен:
), модуль которого равен:
c = a · b sin α.
Направлен этот вектор  перпендикулярно плоскости, в которой расположены векторы
перпендикулярно плоскости, в которой расположены векторы  и
и  , в сторону, откуда кратчайший поворот от вектора
, в сторону, откуда кратчайший поворот от вектора  к вектору
к вектору  происходит против направления хода часовой стрелки.
происходит против направления хода часовой стрелки.
Теперь определим модуль линейной скорости  точки М. На основании формулы будем иметь:
точки М. На основании формулы будем иметь:
 = ωR.
= ωR.
Из схемы рис. 2.17 видим, что
R = rsinα,
тогда
 = ω · R = ω · rsinα,
= ω · R = ω · rsinα,
где  — радиус-вектор точки М относительно центра О; α — угол между векторами
— радиус-вектор точки М относительно центра О; α — угол между векторами  и
и  .
.

Если сравнить предыдущее выражение с векторным произведением двух векторов, то по модулю имеем третий вектор, которым и является вектор  .
.
Покажем направление вектора  линейной скорости точки M, который будет расположен на касательной к окружности, образованное траекторией движения точки M, или по перпендикуляру к плоскости треугольника OMC.
линейной скорости точки M, который будет расположен на касательной к окружности, образованное траекторией движения точки M, или по перпендикуляру к плоскости треугольника OMC.
Далее определим модуль векторного произведения  х
х  :
:
| х
х  | = ω rsinα.
| = ω rsinα.
Направление векторного произведения, как результирующего вектора, показанный
на рис. 2.17, он также перпендикулярен плоскости ΔОМС. Из этого можно сделать вывод, что не только совпадают модули линейной скорости и векторного произведения, но совпадают и их направления. Отсюда:
 =
=  х
х  .
.
Таким образом, линейная скорость любой точки тела, вращается вокруг неподвижной оси, равна векторному произведению двух векторов: угловой скорости и радиус-вектора этой точки относительно произвольной точки оси вращения.
Определим линейную скорость точки M тела, ось вращения которого произвольно расположена в пространстве относительно декартовой системы отсчета Oxyz (рис. 2.18). Координаты точки M — x, y, z, проекции вектора угловой скорости  — ωx ωy ωz; проекции радиус-вектора
— ωx ωy ωz; проекции радиус-вектора  — такие же координаты x, y, z.
— такие же координаты x, y, z.
Выразим линейную скорость  с помощью определителя векторного произведения:
с помощью определителя векторного произведения:

Как известно, вектор  можно записать через его проекции:
можно записать через его проекции:

Тогда, сравнивая последние два выражения, проекции линейной скорости  на оси координат равны:
на оси координат равны:

Выражения получены Эйлером в 1765 г.
Для случая на рис. 2.17:
ωx = 0,
ωy = 0,
ωz = 0,
откуда, пользуясь выражением, будем иметь:



Пример:
Вращения маховика двигателя в пусковой период определяется уравнением  , где t — в секундах, φ — в радианах. Определить модуль и направление ускорения точки, расположенной на расстоянии 50 см от оси вращения, в момент, когда ее скорость равна
, где t — в секундах, φ — в радианах. Определить модуль и направление ускорения точки, расположенной на расстоянии 50 см от оси вращения, в момент, когда ее скорость равна  1 = 8 м/с .
1 = 8 м/с .
Решение.
Для определения ускорения движения материальной точки можно использовать выражение:

Угловые скорость и ускорение движения маховика двигателя определим использовав выражения:

Определим момент времени, в который нужно определить ускорение точки. Для этого, на основании предыдущего выражения, определим угловую скорость вращения маховика:

Поскольку определена ранее угловая скорость равна ω = t2, то можем определить время t1:

В определенное выше угловое ускорение, равное ε = 2t, подставим значение времени t1, получим его значение
ε1 = 2t1 = 2 · 4 = 8 с–2 .
Подставим окончательно значение ω1 и ε1 в выражение для полного ускорения, получим искомый результат

Направление вектора  определим по выражению:
определим по выражению:

откуда
φ = 1º 48´,
где φ — угол между радиусом вращения и вектором ускорения  .
.
Векторное выражение нормального и тангенциального ускорений
Для определения векторного выражения линейной скорости произвольной точки тела, вращающейся вокруг неподвижной оси, составим расчетную схему (рис. 2.19). Также, как и в случае векторного выражения линейной скорости точки тела, рассматриваем произвольную точку M на теле, которое вращается вокруг неподвижной оси z. Направление вращения тела показано стрелкой. Точка M движется по траектории, созданной кругом с центром С, расположенным на оси вращения z и радиусом R. С любой точки O на оси вращения z проведен к точке M радиус — вектор  . Поскольку вращения тела вокруг оси z является ускоренным, то с точки O отложены векторы угловой скорости
. Поскольку вращения тела вокруг оси z является ускоренным, то с точки O отложены векторы угловой скорости  и углового ускорения
и углового ускорения  . С точкой M связан вектор линейной скорости
. С точкой M связан вектор линейной скорости  , который направлен по касательной, проведенной через точку M в круг, образованного траекторией ее движения. На этой же касательной показан вектор касательной
, который направлен по касательной, проведенной через точку M в круг, образованного траекторией ее движения. На этой же касательной показан вектор касательной  составляющей линейного ускорения точки M, направленный в ту же сторону, что и вектор
составляющей линейного ускорения точки M, направленный в ту же сторону, что и вектор  . Вдоль радиуса R окружности, описываемой траекторией движения точки M, показанный
. Вдоль радиуса R окружности, описываемой траекторией движения точки M, показанный
вектор  — нормальной составляющей линейного ускорения.
— нормальной составляющей линейного ускорения.

Для получения векторных формул нормального и тангенциального ускорений возьмем производную по времени от выражения выше, подставляя в него выражение:

Анализируя выражение и рассматривая рис. 2.19, можно записать, что  — вектор углового ускорения, который направляется аналогично вектора угловой скорости
— вектор углового ускорения, который направляется аналогично вектора угловой скорости  , а
, а  — вектор линейной скорости.
— вектор линейной скорости.
Подставим последние значения в выражение, получим
 =
=  х
х  +
+  х
х  =
=  х
х  +
+  х (
х ( х
х  ).
).
Выражение называют формулой Ривальса.
Проведем анализ выражения.
Модуль первого векторного произведения будет равен:
| х
х  | = εr sin α.
| = εr sin α.
Модуль тангенциального ускорения будет равен:
a = εR = εr sin α.
= εR = εr sin α.
Как видно из последних выражений совпадают не только их модули, но и направления (┴ΔОМС), поэтому
 =
=  х
х  .
.
Тангенциальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора углового ускорение на радиус-вектор этой точки относительно произвольной точки оси вращения.
Модуль нормального ускорения будет равен:
an = ω2 R = ω .
.
Модуль векторного произведения | х
х  | =
| =  поскольку
поскольку 
Сопоставляя значения модулей векторов  ,
,  х
х  и их направления, можно сделать вывод, что
и их направления, можно сделать вывод, что
 =
=  х
х  =
=  х (
х ( х
х  ).
).
Нормальное ускорение точки твердого тела, вращающегося вокруг неподвижной оси, равно векторному произведению вектора угловой скорости на вектор линейной скорости этой точки.
Передача вращательного движения
Передача вращательного движения осуществляется с помощью зубчатых, ременных, цепных передач, колес трения и т. д.
Рассмотрим передачу вращательного движения с помощью зубчатой передачи (или фрикционной передачи) (рис. 2.20), которая состоит из двух колес, вращающихся вокруг неподвижных осей. Назовем первое колесо (меньшего диаметра) ведущим. Направление его вращения показано стрелкой. Оно имеет такие физические и кинематические параметры: радиус — r1, количество зубов — z1, угловая скорость – ω1 или частота вращения – n1. Второе колесо, которое является ведомым, имеет следующие параметры: радиус — r2, количество зубов — z2, угловая скорость — ω2 или частота вращения — n2. Направление вращения второго колеса также показано стрелкой.
Теперь, если передача вращательного движения осуществляется без проскальзывания в месте контакта колес, то линейная скорость точки контакта (точка А), которая принадлежит одновременно двум колесам, должна быть одинаковой. Найдем линейные скорости точки A начала для первого колеса, а затем для второго колеса и приравняем их. Линейная скорость точки А для первого колеса равна:
 А = ω1 · r1 ,
А = ω1 · r1 ,
а линейная скорость точки А для второго колеса будет равна:
 А = ω2 · r2 .
А = ω2 · r2 .
Приравняв выражения, будем иметь:
ω1 · r1 = ω2 · r2 .

Преобразуем выражение следующим образом:
 =
=  .
.
Если считать, что передаточное отношение, это = u, то можно окончательно написать:
= u, то можно окончательно написать:

Таким образом, передаточное отношение, это отношение угловой скорости ведущего колеса к угловой скорости ведомого колеса, которое равно отношению радиуса (или числа зубьев) ведомого колеса к радиусу ведущего колеса.
В технике есть такое понятие, как передаточное число.
Передаточное число —это отношение большей угловой скорости до меньшей.
Указанные основные положения о передаче вращательного движения между двумя колесами полностью пригодны для определения передаточного отношения для ременной или цепной передач. На рис. 2.21 показана схема ременной (цепной) передачи с указанием физических и кинематических параметров. Для определения передаточного отношения этой передачи необходимо использовать выражение (2.64).
Передаточное отношение может быть больше единицы или меньше.
Если передача вращательного движения осуществляется с помощью, так называемой червячной передачи (рис. 2.22), то передаточное отношение определяется формулой:

где zk — число зубьев червячного колеса; h — число заходов червяка.


Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Движение твердого тела разделяют на виды:
- поступательное;
- вращательное по неподвижной оси;
- плоское;
- вращательное вокруг неподвижной точки;
- свободное.
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Рисунок 1. Поступательное криволинейное движение кабин колеса обзора
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Если имеется поступательное движение, то общая скорость для всех точек тела υ→ называется скоростью поступательного движения, а ускорение a→ – ускорением поступательного движения. Изображение векторов υ→ и a→ принято указывать приложенными в любой точке тела.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось Az, полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2.
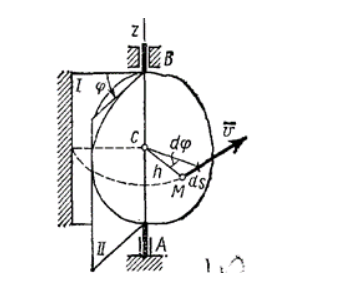
Рисунок 2. Угол поворота тела
Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t, то есть φ=f(t). Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε.
Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ, скорость υ на угловую скорость ω, а ускорение a на угловое ε.
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s=υ·t | φ=ω·t |
| υ=const | ω=const |
| a=0 | ε=0 |
| Равнопеременное | |
| s=υ0t±at22 | φ=ω0t±ε·t22 |
| υ=υ0±a·t | ω=ω0±ε·t |
| a=const | ε=const |
| Неравномерное | |
| s=f(t) | φ=f(t) |
| υ=dsdt | ω=dφdt |
| a=dυdt=d2sdt2 | ε=dωdt=d2φdt2 |
Задачи на вращательное движение
Дана материальная точка, которая движется прямолинейно соответственно уравнению s=t4+2t2+5. Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.
Дано: s=t4+2t2+5, t=2 с.
Найти: s; υ; υ; α.
Решение
s=24+2·22+5=29 м.
υ=dsdt=4t3+4t=4·23+4·2=37 м/с.
υ=∆s∆t=292=14,5 м/с.
a=dυdt=12t2+4=12·22+4=52 м/с2.
Ответ: s=29 м; υ=37 м/с; υ=14,5 м/с; α=52 м/с2
Задано тело, вращающееся вокруг неподвижной оси по уравнению φ=t4+2t2+5. Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.
Дано: φ=t4+2t2+5, t=2 с.
Найти: φ; ω; ω; ε.
Решение
φ=24+2·22+5=29 рад.
ω=dφdt=4t3+4t=4·23+4·2=37 рад/с.
ω=∆φ∆t=292=14,5 рад/с.
ε=dωdt=122+4=12·22+4=52 рад/с2.
Ответ: φ=29 рад; ω=37 рад/с; ω=14,5 рад/с; ε=52 рад/с2.