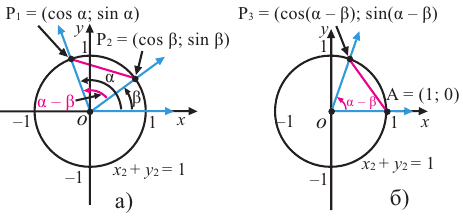
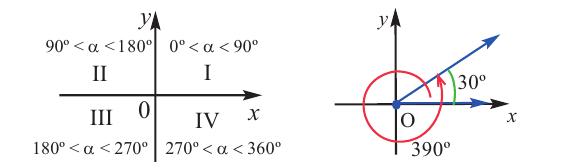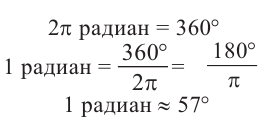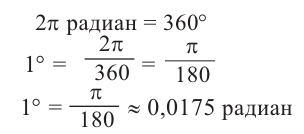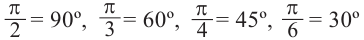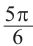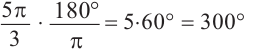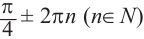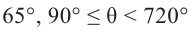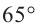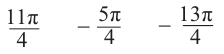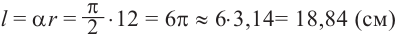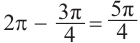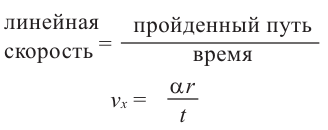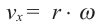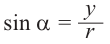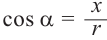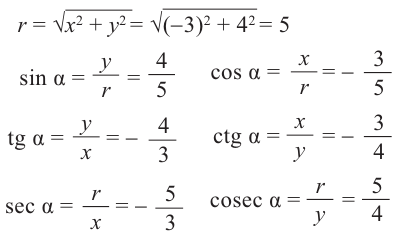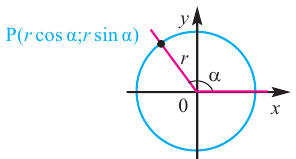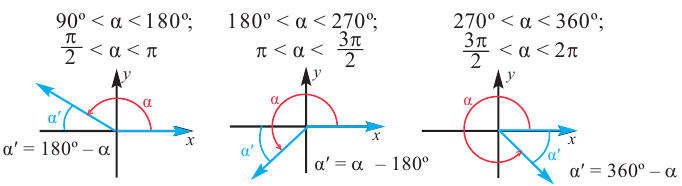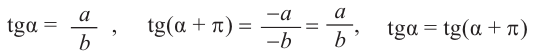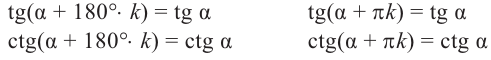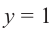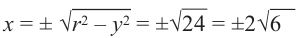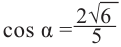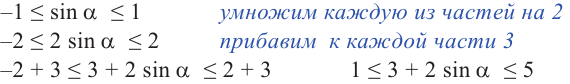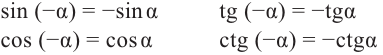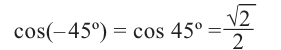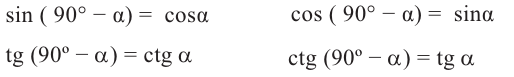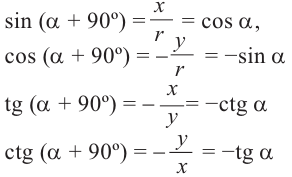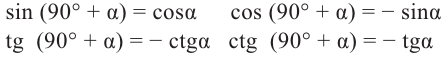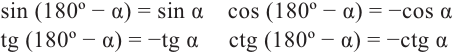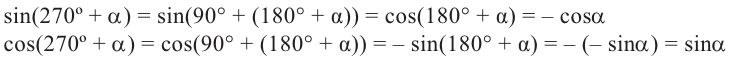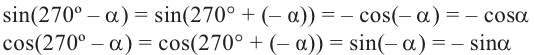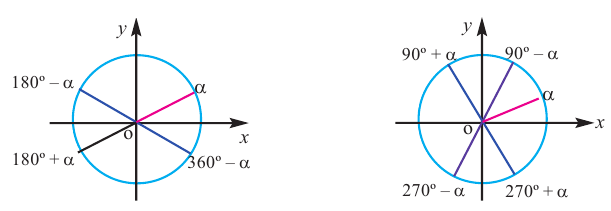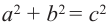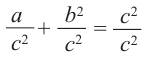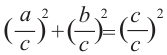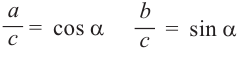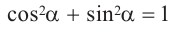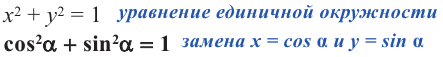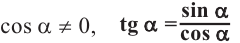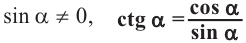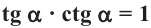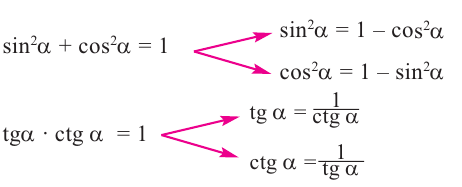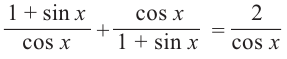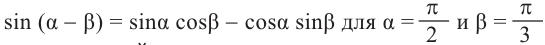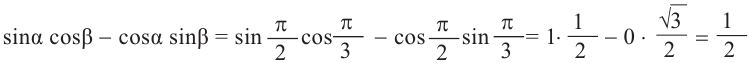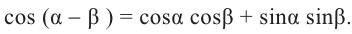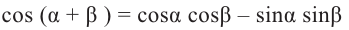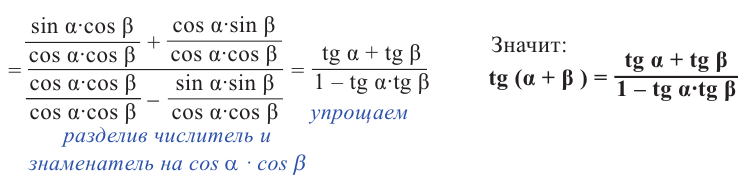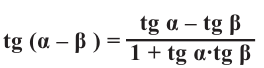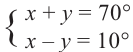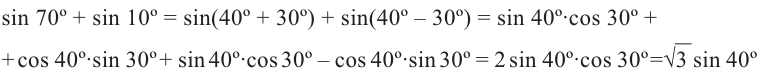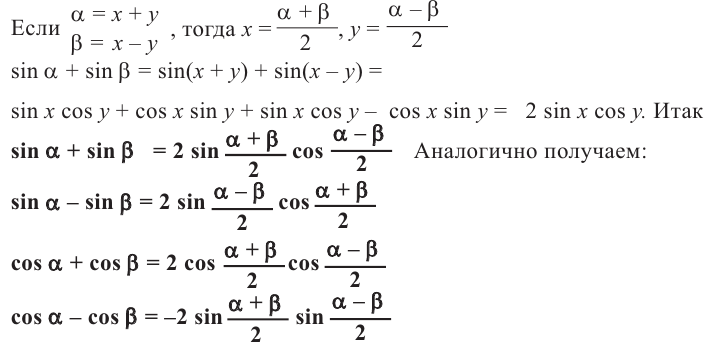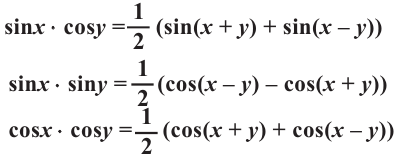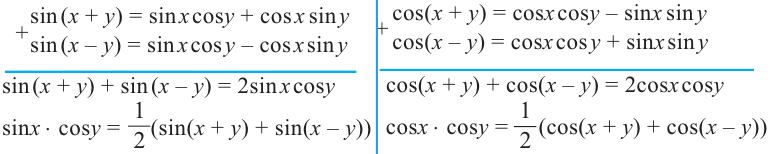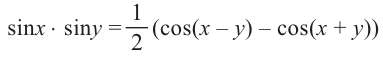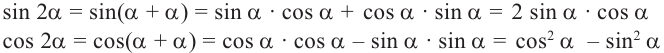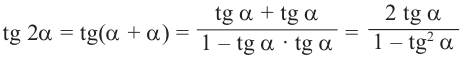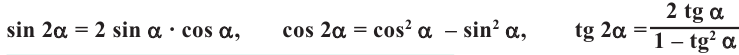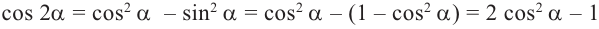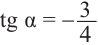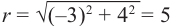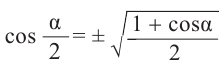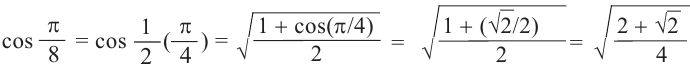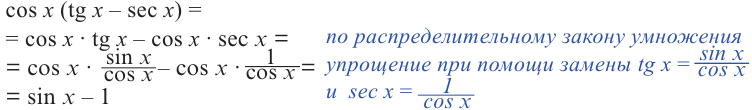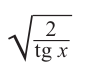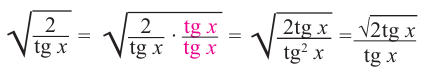Содержание:
Тригонометрические функции произвольного угла
Угол поворота
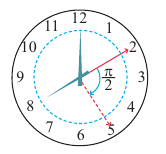
До недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
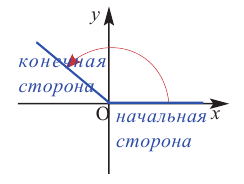
Начальное положение луча соответствует одной стороне угла, конечное положение – другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
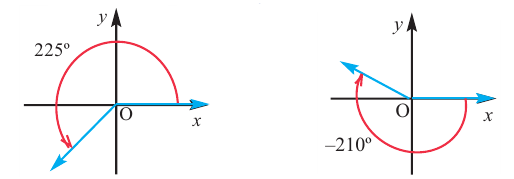
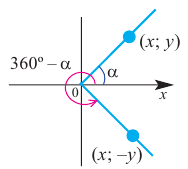
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
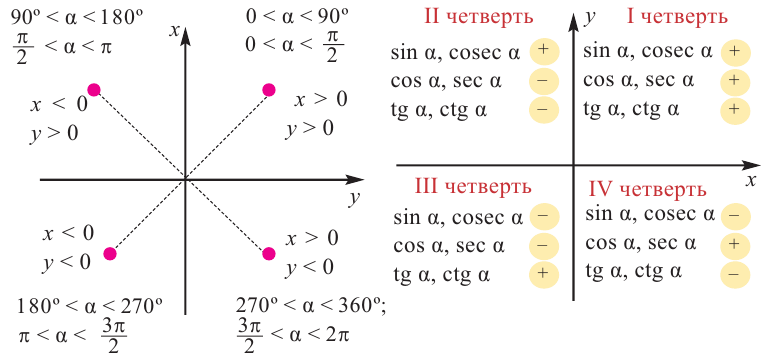
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
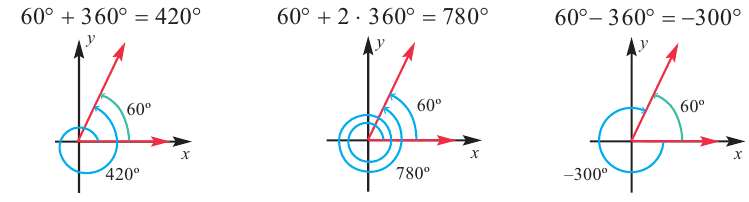
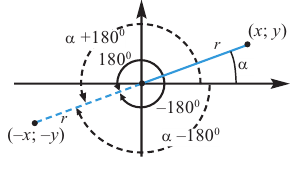
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота 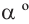
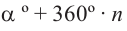
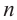
Радианная и градусная мера угла
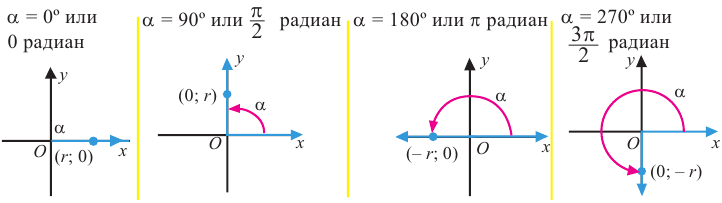
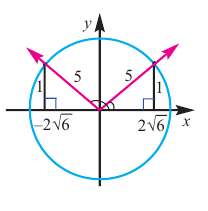
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
Радианное измерение углов
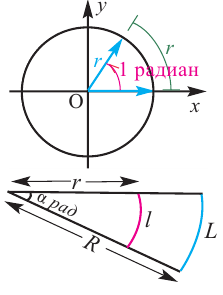
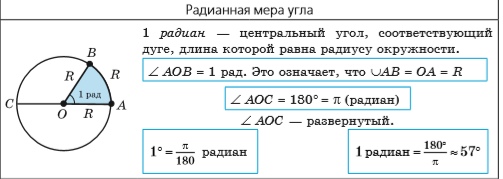
Угол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: 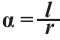
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности 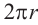
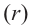
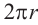
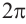
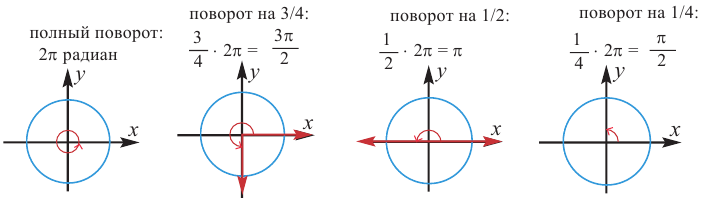
Радианная мера одного целого оборота равна 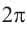
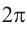
Преобразование градусов в радианы:
Таким образом, 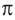
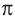
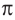
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° =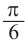
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° =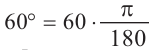
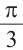

б)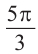
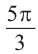
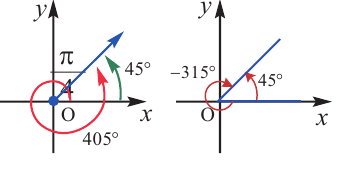
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: 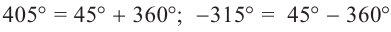
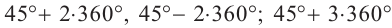
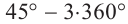
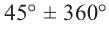
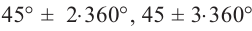
В радианах это можно записать как
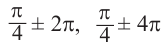
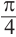
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле 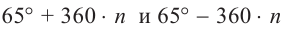
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д)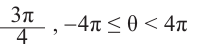
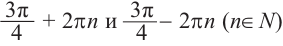
Интервалу 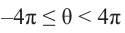
Длина дуги
Запишем формулу нахождения длины дуги, соответствующей центральному углу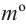
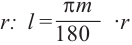
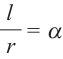
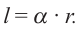
Площадь сектора
Центральному углу 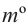
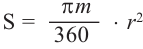
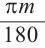
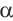
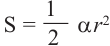
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует 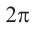
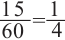
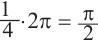
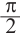
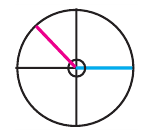
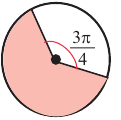
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
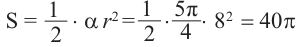
Периметр сектора равен сумме длин двух радиусов и длины дуги: 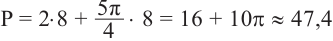
Линейная скорость и угловая скорость
Скорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае – используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
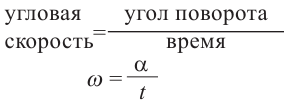
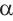
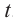
линейная скорость = 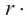
Пример 3. Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу 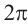
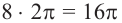
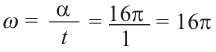
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость: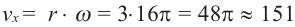
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость: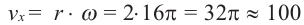
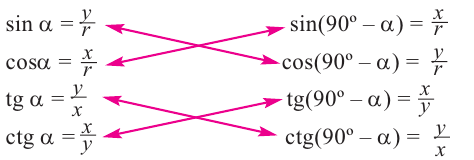
Тригонометрические функции
Тригонометрические отношении для угла зависят только от значения угла.
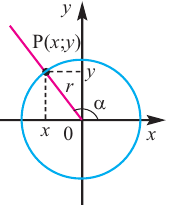
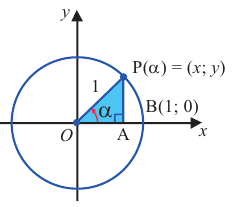
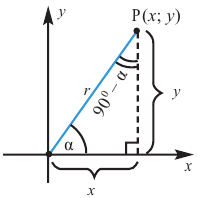
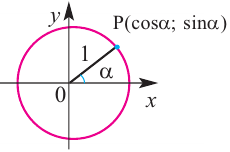
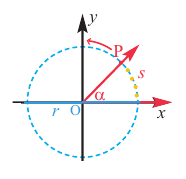
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).

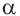

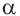

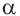
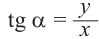
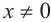

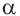
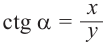
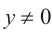

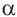
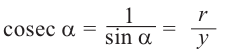
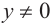

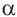
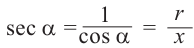
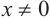
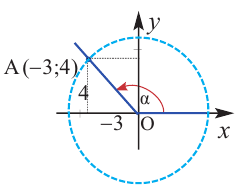
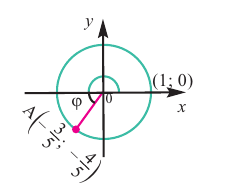
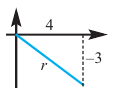
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота 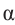
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота 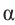
Решение:
а)
б)
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота 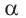
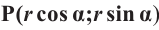
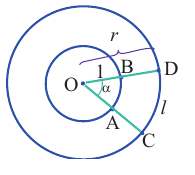
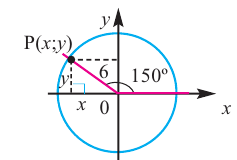
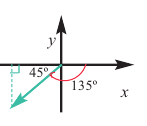
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
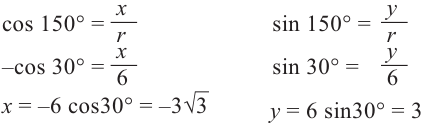
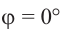
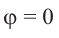
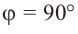
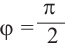
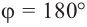
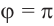
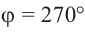
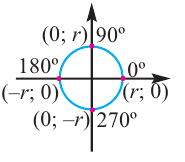
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
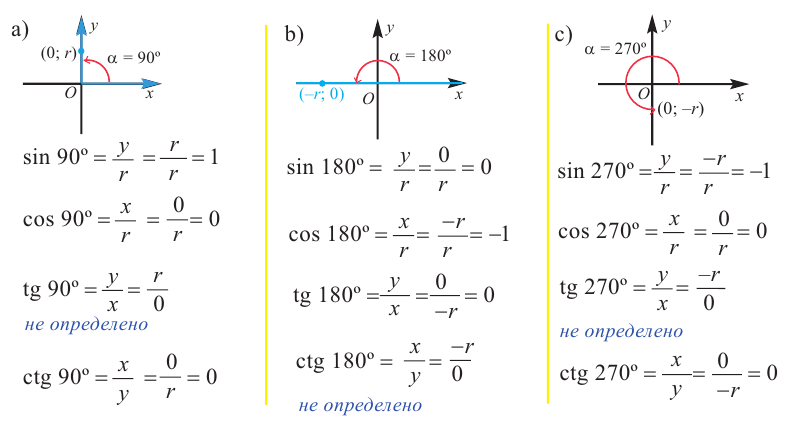
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению 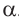
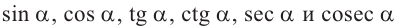
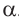
Так как 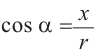
Так как 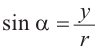
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Чтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота 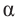
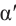
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов – при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а)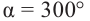
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
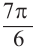
Пример 2. Найдём значение основных тригонометрических функций для угла 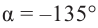
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° – 180° = 45°.
3.Определим какой четверти принадлежит угол -135° – угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
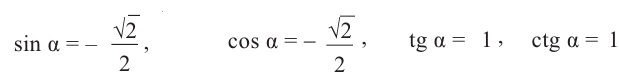
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
Так как конечные стороны углов 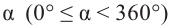
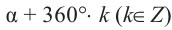
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота 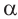
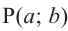
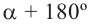

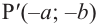
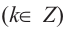
Пример 3. Найдём допустимые значения 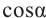
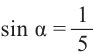
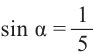
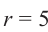
Абсцисса этой точки
Тогда 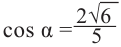
Единичная окружность и тригонометрические функции
Значения тригонометрических функций зависят только от значения угла 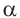
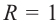
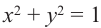
Если точка 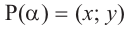
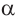
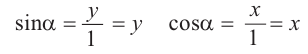
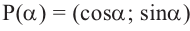
Также по заданным координатам можно найти следующие тригонометрические функции: 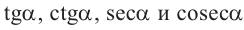
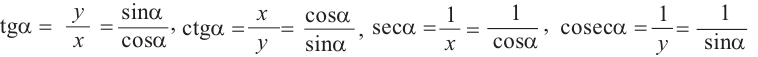
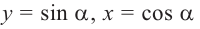
Для этого надо выполнить следующие шаги:
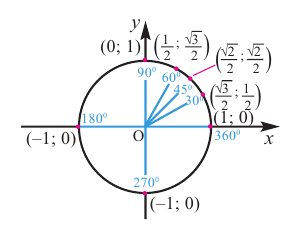
1) На единичной окружности отметим точки, соотвегствующие углу поворота 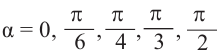
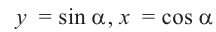
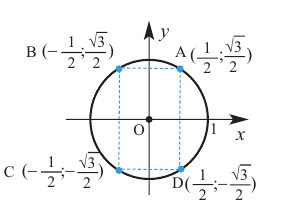
2)Для некоторой точки, принадлежащей единичной окружности, например 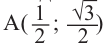
Точка В симметрична точке А относительно оси у, точка С – относительно начала координат, а точка D – относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
- Заказать решение задач по высшей математике
Единичная окружность и тригонометрические функции произвольного угла
Так как координаты точек на единичной окружности удовлетворяют условиям 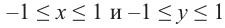
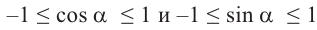
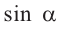
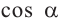
Пример 1. Для угла поворота 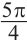
Решение: Конечная сторона угла поворота 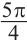
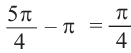
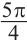
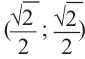
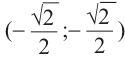
Тогда ,
Пример 2. Точка А, с абсциссой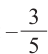
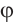
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла 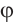
Решение:
а)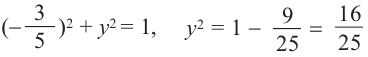
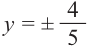
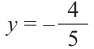
б)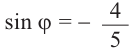
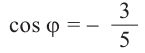
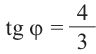
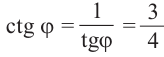
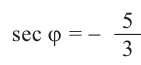
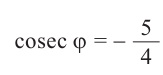
Пример 3. Найдём наибольшее и наименьшее значение выражения 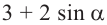
Решение:
Таким образом, для выражения 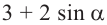
Формулы приведения
Если объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
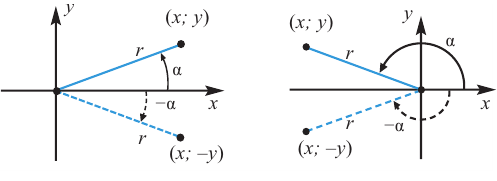
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов 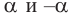
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
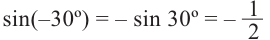
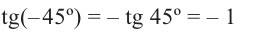
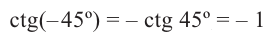

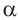
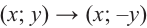
Отсюда получаем:
Запишем для углов 


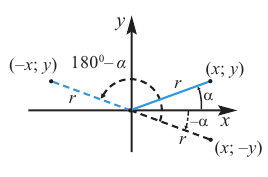
При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов 

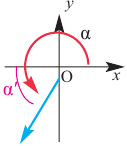
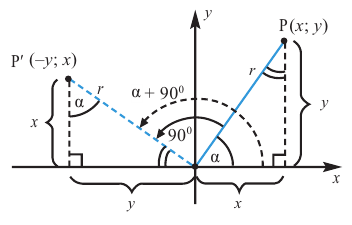
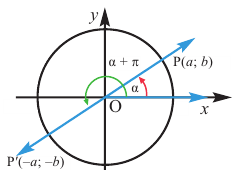
Повернём конечную сторону угла поворота 
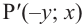
Запишем эти формулы в следующем виде:
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
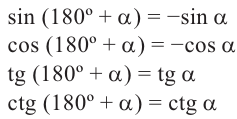
Пример 2.
Для получения аналогичных формул тригонометрических функций угла поворота 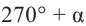
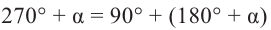
Например:
Теперь запишем соответствующие формулы для угла поворота 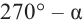
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид 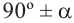
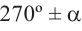
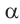
2)Если аргумент имеет вид 180° ± 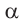
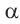
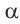
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла 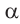
Тригонометрические тождества
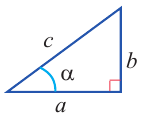
Для острого угла 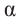
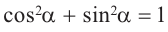
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же угла
Тождество 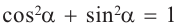
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений 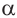
Для всех значений 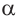
Из данных равенств имеем,что если для угла 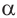
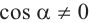
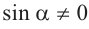
Разделив обе чаете равенства 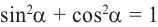
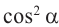
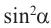
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что 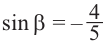
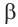
остальные тригонометрические функции.
Из формул 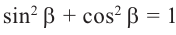
Так как угол 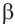
Тогда:
Формулы сложения
Практическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений 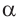
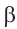
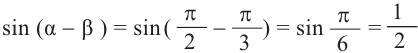
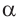
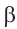
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° – 30°)?
Тригонометрические функции суммы и разности двух углов.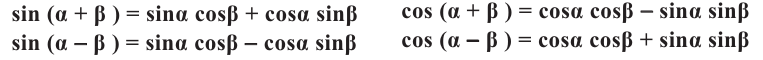

На рисунке
а)для угла 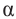
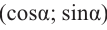
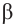
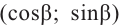
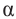
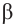
Тогда, для угла 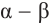
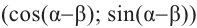
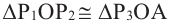
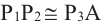

учитывая, что
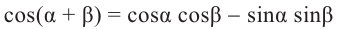

no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.

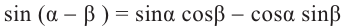
Пример 1. Найдём значение выражения 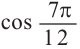
Решение.
Пример 2.
Найдём значение выражения 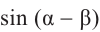
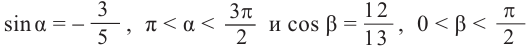
Решение.
Известно что 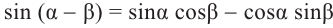
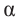
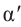
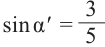
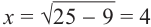
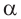
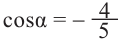
Аналогично, если зная, что 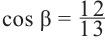
что 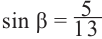
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложения
Практическая работа.
Преобразуйте сумму 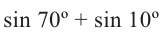
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° – 30° и упростите
Преобразование суммы(разности) в произведение
Формулы преобразования произведения
Справедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.
Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить 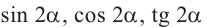
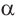
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргумента
Имеем, что
Отсюда: 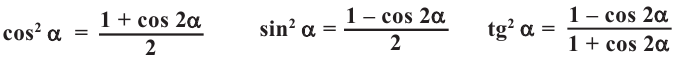
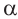
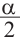
Для половинных аргументов справедливы тождества. 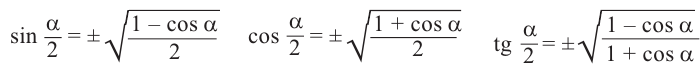
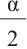
Пример 1. Упростим выражение 
Решение.
Пример 2. He используя калькулятор, вычислим значения 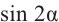
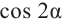

Решение.
Пример 3. Найдём значений 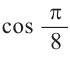
Решение:
Используем формулу половинного аргумента
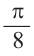
Упрощение тригонометрических выражений
Пример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь 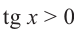
- Теоремы синусов и косинусов
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
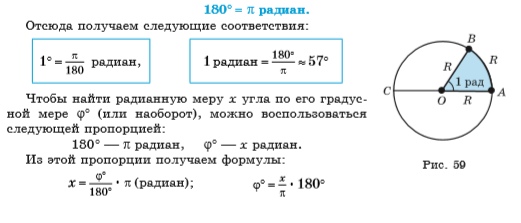
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° – градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
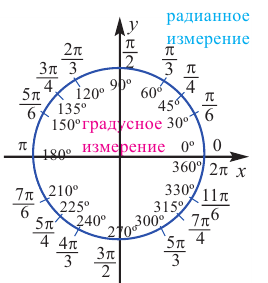
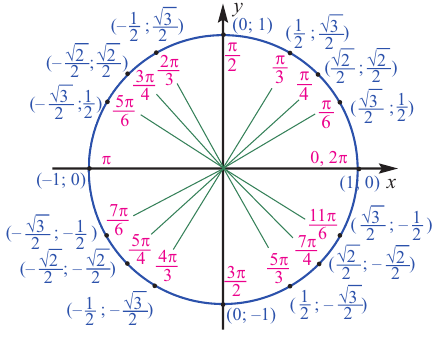
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost
[/spoiler]
Онлайн калькулятор для перевода углов из радиан в градусы и обратно, интерактивная таблица градусов и радиан.
Формула перевода радианов в градусы: x°=храд⋅180/π
Точное число чему равен 1 радиан в градусах:
1 радиан = 57.29577951308 градуса
Радиан (обозначение: рад, rad) — угол, соответствующий дуге, длина которой равна её радиусу.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

План урока
- Введение понятий радианной меры угла, угла в один радиан
- Формула перевода радианной меры угла в градусную
- Формула перевода градусной меры угла в радианную
- Решение задач на применение формул перевода градусной меры угла в радианную и наоборот
- Длина окружности для дуги в α радиан
- Площадь кругового сектора в α радиан
- Решение задач на применение формул нахождения длины окружности и площади кругового сектора
Цели урока
- Знать определение угла в 1 радиан, формулы перевода градусной меры в радианную и наоборот
- Уметь использовать формулы перевода градусной меры в радианную и наоборот при решении задач, вычислять длину окружности и площадь кругового сектора
Разминка
- Определение центрального угла, вписанного угла.
- Как найти центральный угол, вписанный угол, если даны градусные меры дуг, на которые они опираются?
- Формула нахождения длины окружности.
- Формула нахождения площади кругового сектора.
Рис. 1
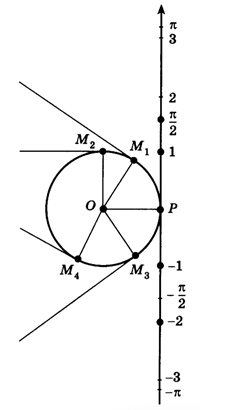
Пусть прямая, расположенная вертикально, и окружность радиуса 1 касаются в точке Р (см. рис. 1). Назовем эту прямую числовой осью с началом в точке Р, направление вверх будем считать положительным, единичным отрезком – радиус окружности. Считая π≈3,14, отметим точки ±1,±π2,±2,±3,±π. Представим данную числовую прямую в виде нерастяжимой нити, закрепим ее на окружности в точке Р и «намотаем» ее на окружность. Тогда точка числовой прямой с координатой 1 попадет в точку М1, π2 в М2, -1 в М3, -π2 в М4. То есть каждой точке числовой прямой ставится в соответствие некоторая точка окружности.
Будем считать угол РОМ1 единичным, т.к. длина дуги РМ1 равна радиусу окружности, который в свою очередь равен 1, и его мерой измерять другие углы. Таким образом угол РОМ2 будет равен π2. В таком случае говорят, что углы измеряются в радианной мере, а угол РОМ1 называют углом в один радиан (1 рад).
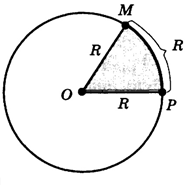
Рис. 2
Пусть дана окружность радиуса R. Отметим на ней радиус ОР, дугу окружности РМ длины R и угол РОМ (см. рис. 2).
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется
углом в один радиан
.
На рисунке 2 угол РОМ является углом в один радиан.
А сколько же градусов содержится в одном радиане? Из курса геометрии мы знаем, что полуокружности (дуга длиной πR) соответствует центральный угол в 180°, тогда если длина дуги R, то ей соответствует угол, в π раз меньший, т.е.
1 рад=(180π)°
Считая π≈3,14, 1 рад≈57,3°.
Если угол равен не 1 рад, а α рад, то
α рад=(180πα)° (1)
Формула (1) называется формулой перевода радианной меры угла в градусную.
Решим обратную задачу. Выведем формулу перевода градусной меры угла в радианную. Так как угол в 180° равен π радиан, то
1°=π180 рад
Если угол содержит α°, то его радианная мера
α°=π180α рад (2)
Формула (2) называется формулой перевода градусной меры угла в радианную.
Найти радианную меру угла, выраженную в градусах:
а) 18°; б) 153°.
Решение
а) π-180°, x-18°
Тогда x=18π180=π10 рад.
б) π-180°, x-153°
Тогда x=153π180=17π20 рад.
Ответ: а) π10 рад; б) 17π20 рад.
Найти градусную меру угла, выраженную в радианах:
а) 0,3π; б) 2,25π; в) 2 рад (с точностью до 0,01°).
Решение
а) π-180°, 0,3π-x°
Тогда x=180×0,3ππ=54°.
б) π-180°, 2,25π-x°
Тогда x=180×2,25ππ=405°.
в) π-180°, 2-x°
Тогда x=180×23,14=114,65°.
Ответ: а) 54°; б) 405°; в) 114,65°.
Найти радианную меру угла, выраженную в градусах:
а) 225°; б) 120°.
Найти градусную меру угла, выраженную в радианах:
а) 0,6π; б) 3,2π.
При решении задач часто применяют следующие обозначения мер углов:
|
Градусы |
0 |
30 |
45 |
60 |
90 |
180 |
|
Радианы |
0 |
π6 |
π4 |
π3 |
π2 |
π |
Так как угол в 1 радиан опирается на дугу радиуса R, то угол α радиан опирается на дугу длиной αR, значит, формула длины окружности для дуги в α радиан
l=αR (3)
Площадь полукруга, т.е. кругового сектора в π рад равна πR22. Значит, круговой сектор в 1 радиан имеет площадь, в π раз меньшую, R22. Тогда, площадь сектора в α радиан равна R2α2.
S=R2α2 (4)
Найти длину l окружности, стягивающей угол в 3 радиана, если радиус R окружности равен 5.
Решение
По формуле (3) длина окружности радиуса 5 для дуги в 3 радиана
l=αR=3×5=15.
Ответ: 15.
Дуге кругового сектора соответствует угол в 5π6 рад. Найти площадь сектора, если радиус круга 2 см.
Решение
По формуле (4) имеем S=R2×α2=22×5π62=5π3 см2.
Ответ: 5π3 см2.
Центральный угол π3 радиан стягивается дугой окружности, длина которой 2 см. Найти радиус этой окружности.
Радиус круга равен 1,5 см, а площадь кругового сектора 2,25 см2. Найти угол, соответствующий дуге этого кругового сектора.
- Что такое радианная мера угла?
- Как перевести градусную меру угла в радианную?
- Как перевести радианную меру угла в градусную?
Ответы
Упражнение 1
а) 5π4; б) 2π3.
Упражнение 2
а) 108°; б) 576°.
Упражнение 3
6π см.
Упражнение 4
2 рад.
§ 11. Радианная мера углов
1. Понятие угла
В геометрии
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки.
В тригонометрии*
Угол — фигура, образованная при повороте луча на плоскости около начальной точки.
2. Измерение углов
Градусная мера углачасть развернутого угла)
Каждому углу ставится в соответствие градусная мера α ∈ [0°; 180°].
Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Угол поворота
α ∈ (–×; +×).
Объяснение и обоснование
1. Понятие угла. В курсе геометрии угол определяется как геометрическая фигура, образованная двумя лучами, которые выходят из одной точки. Например, угол AOB, изображенный в первом пункте таблицы 16, — это угол, образованный лучами OA и OB.
Угол можно рассматривать также как результат поворота луча на плоскости около начальной точки. Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.
2. Измерение углов. Данные выше различные определения угла приводят к различному пониманию измерения углов.
В курсе геометрии каждому углу соответствует его градусная мера, которая может находиться только в пределах от 0° до 180°, и поэтому, например, для прямого угла AOB его мера записывается однозначно: ∠ AOB = 90° (1° — это 1/180 часть развернутого угла).
При измерении углов поворота договорились, что направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным.
Поэтому при измерении углов, образованных при повороте луча около начальной точки, мы можем получить как положительные, так и отрицательные значения углов поворота. Например, если угол AOB, в котором лучи ОА и ОВ являются взаимно перпендикулярными, получен при повороте луча OA на угол 90° против часовой стрелки, то значение угла поворота β (см. соответствующий рисунок в пункте 2 табл. 16) равно +90° (или просто 90°). Если тот же угол AOB получен при повороте луча OA на угол 270° по часовой стрелке (понятно, что полный оборот — это 360°), то значение угла поворота γ равно (–270°). Этот же угол AOB можно получить также при повороте луча OA против часовой стрелки на 90° и еще на полный оборот; в этом случае значение угла поворота ϕ равно 90° + 360°, то есть 450° и т. д.
Выбрав как значение угла поворота произвольное отрицательное или положительное число (градусов), мы всегда можем повернуть луч OA (по часовой стрелке или против нее) и получить соответствующий угол AOB. Таким образом, величина угла поворота (в градусах) может принимать все действительные значения от.
Для измерения углов принимают определенный угол за единицу измерения и с ее помощью измеряют другие углы.
За единицу измерения можно принять любой угол, например один градус (1°) — 1/180 часть развернутого угла.
В технике за единицу измерения углов принимают полный оборот (заметим, что 1 градус — это 1/360 часть полного оборота).
В мореходстве за единицу измерения углов принимают румб, равный 1/32 час ти полного оборота.
В математике и физике, кроме градусной меры углов, используется также радианная мера углов.
Если рассмотреть некоторую окружность,
то 1 радиан — это центральный угол, соответствующий дуге, длина которой равна радиусу окружности.
Таким образом, если угол AOB равен одному радиану (рис. 59), то это означает, что ∪AB = OA = R.
Установим связь между радианной и градусной мерами углов. Центральному развернутому углу AOC, с градусной мерой 180°, соответствует полуокружность, то есть дуга, длина которой равна πR, а углу в один радиан — дуга длиной R. Итак, радианная мера развернутого угла AOC равна радиан. Таким образом, одному и тому же развернутому углу АОС соответствует градусная мера 180° и радианная мера π радиан. Это соответствие часто записывают так:
Задача 1 Выразите в радианах величины углов, градусная мера которых равна: 30°; 45°; 60°; 90°; 270°; 360°.
Поскольку 30° — это 1/6часть угла 180°, то из соответствия 180° = π (рад)
получаем, что 30°=6/π (рад).
Аналогично можно вычислить и величины других углов.
В общем случае учитываем, что 1°=π/180 радиан, тогда:
Поскольку радианными мерами рассмотренных углов приходится пользоваться достаточно часто, запишем полученные результаты в виде справочной таблицы:
Замечание. Чаще всего при записи радианной меры углов наименование единицы измерения «радиан» (или сокращенно рад) не пишут, но подразумевают его. Например, вместо равенства 90 2 °=π радиан пишут иногда 90 °=π/2 .
Задача 2 Выразите в градусах величины углов, радианнная мера которых равна: π/10 ; 2π/3 ; 3π/4 ; 5.
Поскольку π/10 — это 1/10 часть угла π, то из соответствия π = 180° получаем, что π/10=18° . Аналогично можно вычислить и величины углов 2π /3 и 3π/4 .
В общем случае учитываем, что 1 радиан=180°/π , тогда:
Отметим, что далее в этом разделе будет рассматриваться в основном радианная мера угла и утверждения будут доказаны для радианной меры угла. Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.
Условимся далее вместо слов «угол, радианная мера которого равна α радиан» говорить коротко «угол α».
Вопросы для контроля
1. Объясните, как можно определить угол с помощью поворота луча. Как при таком определении измеряются углы?
2. Как вы понимаете такие утверждения: «Величина угла равна 450°», «Величина угла равна (–225°)»? Изобразите эти углы.
3. Как можно определить угол в 1°?
4. Дайте определение угла в 1 радиан.
5. Чему равна градусная мера угла в π радиан?
6. Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот — по градусной мере угла найти его радианную меру.
Упражнения
1°. Изобразите угол, образованный поворотом луча OA около точки O на: 1) 270°; 2) –270°; 3) 720°;
4) –90°; 5) 225°; 6) –45°;
7) 540°; 8) –180°; 9) 360°; 10) –60°.
2°. Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?
3. Выразите в радианной мере величины углов, градусная мера которых равна:
1 °) 225°; 2°) 36°; 3) 100°; 4) –240°; 5) –22,5°; 6) –150°.
4. Выразите в градусной мере величины углов, радианная мера которых равна:
1) 3π; 2) 3 4 π; 3) −2 5 π;
4) 7 6 π; 5) − π 18 ;
6) 11 6 π;7) −π 8 ; 8) 3.
5. С помощью калькулятора (или таблиц) найдите радианные меры углов, градусная мера которых равна:
1) 27°; 2) 132°; 3) 43°; 4) 114°.
6. С помощью калькулятора (или таблиц) найдите градусные меры углов, радианная мера которых равна:
1) 0,5585; 2) 0,8098; 3) 3,1416; 4) 4,4454.