Как найти угол поворота в сопромате

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

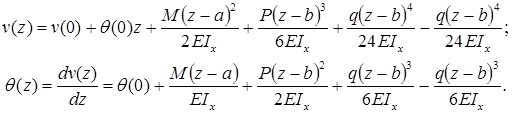
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

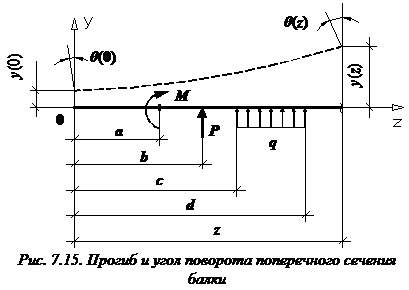
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 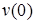и угол поворота 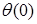балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

Определим прогиб балки на консоли при 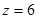м, то есть 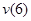. Запишем универсальное уравнение упругой линии балки:

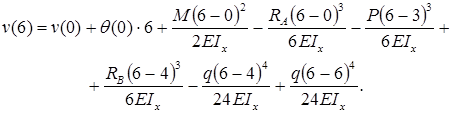
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .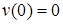

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

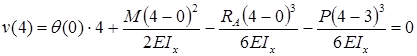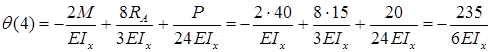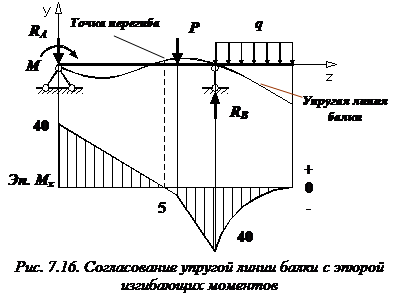
Прогиб консоли при z=6м:

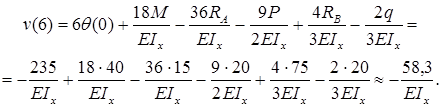
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.

Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.

Верещагин и его метод, правило или способ

А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:​

({ V={ M }_{ F } }cdot overline { M } ={ omega }_{ C }cdot { overline { M } }_{ C } )​

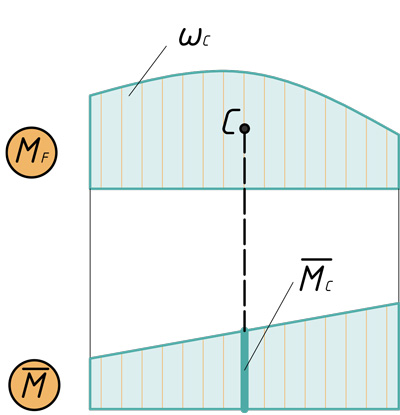
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ω_с — площадь первой эпюры, M_c — ордината второй эпюры под центром тяжести первой.

Площадь и центр тяжести эпюр

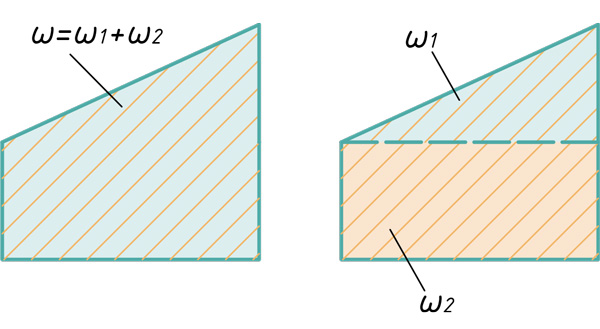
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.

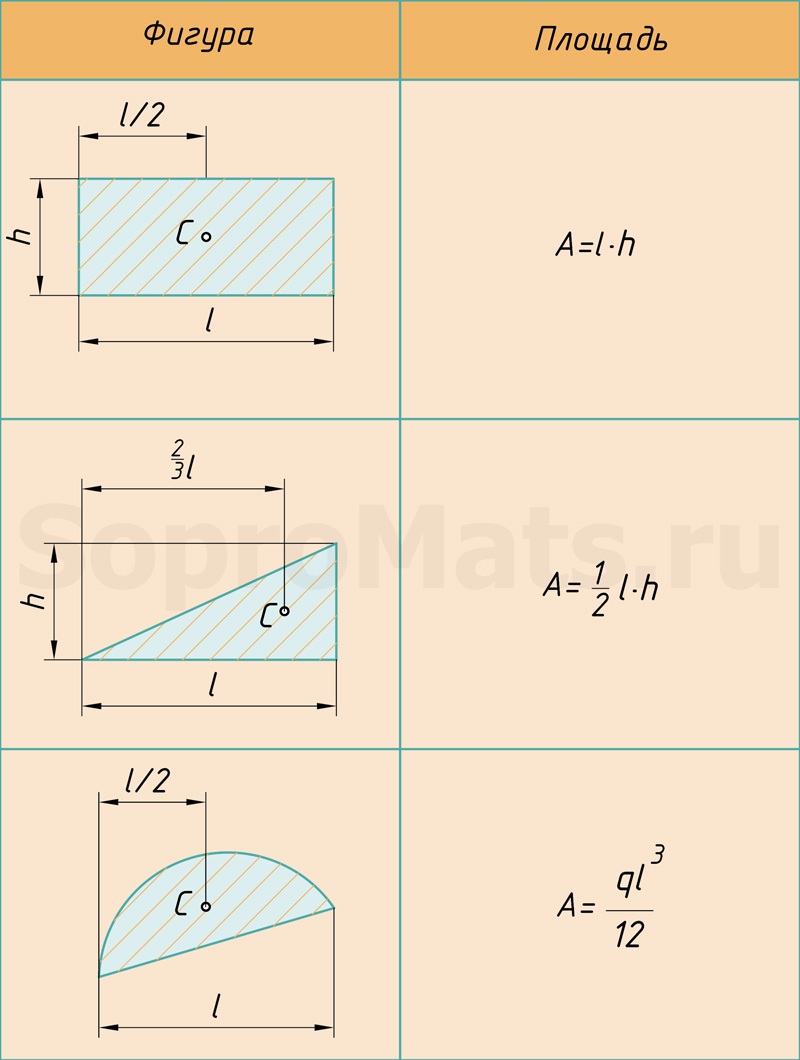
Любой самый сложный участок эпюры  можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.

Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:

Перемножение простейших эпюр по Верещагину

В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.

Прямоугольник на прямоугольник

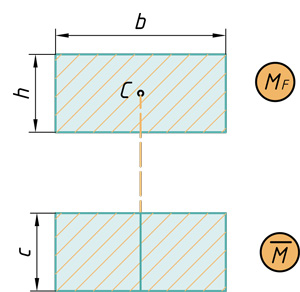
​( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot c } )​

Прямоугольник на треугольник

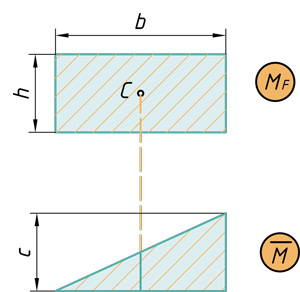
​( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot frac { 1 }{ 2 } cdot c } )​

Треугольник на прямоугольник

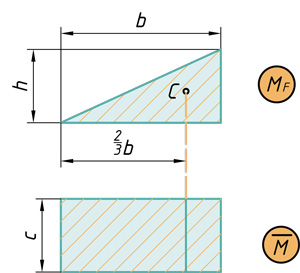
​( { V={ M }_{ F } }cdot overline { M } ={ frac { 1 }{ 2 } cdot bcdot hcdot c } )​

Параболический сегмент на прямоугольник

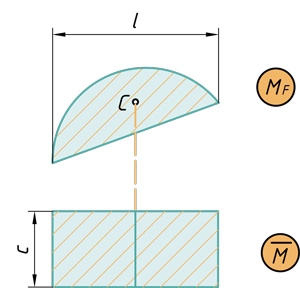
​( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot c } )​

Параболический сегмент на треугольник

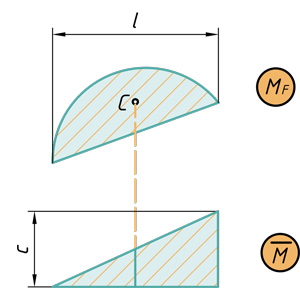
​( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot c } )​

Расслоение эпюр на простые фигуры

В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.

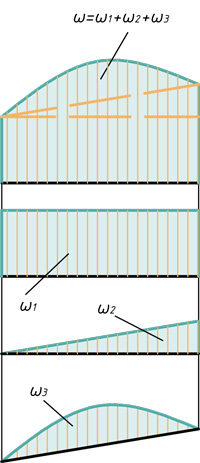
Прямоугольник и треугольник

Два треугольника

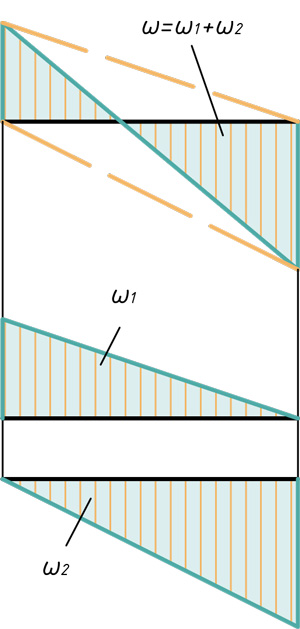
Два треугольника и параболический сегмент

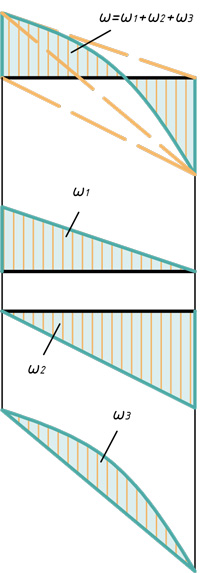
Треугольник, прямоугольник и параболический сегмент

Пример определения перемещений: прогибов и углов поворотов по Верещагину

Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.

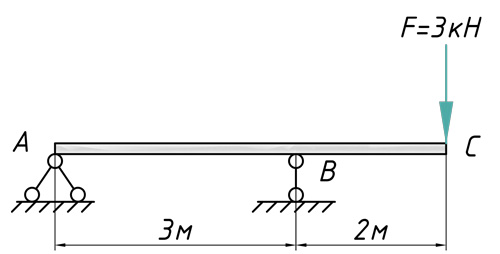
Построение эпюры изгибающих моментов

В первую очередь рассчитываем и строим эпюру изгибающих моментов:

Построение единичных эпюр

Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:

• для прогибов прикладываются единичные силы.
• для углов поворотов прикладываются единичные моменты.

Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.

Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.

Перемножение участков эпюры по Верещагину

После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.

Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.

Определение прогиба сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:

[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 2 }{ 3 } cdot 2+frac { 1 }{ 2 } cdot 6cdot 2cdot frac { 2 }{ 3 } cdot 2)=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } ]

Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:

[ { V }_{ C }=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =frac { 20cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =0.289см ]

Определение угла поворота сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:

[ { theta }_{ C }=frac { 1 }{ E{ I }_{ x } } (-frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 1 }{ 3 } cdot 1)=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } ]

[ { { theta } }_{ C }=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-frac { 3cdot { 10 }^{ 7 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =-0.0004рад ]

Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

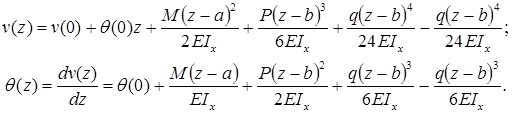
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 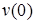и угол поворота 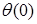балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

Определим прогиб балки на консоли при 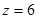м, то есть 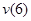. Запишем универсальное уравнение упругой линии балки :

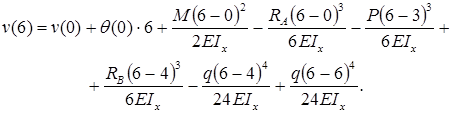
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .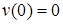

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

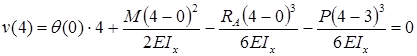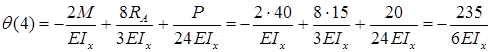Прогиб консоли при z=6м:

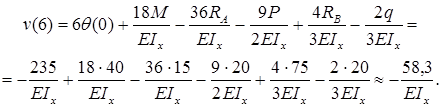
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Расчет прогиба балки методом начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_k – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_k, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, V O и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть V_O=0 и θ_O=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах .

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10 5 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см 4 ). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Расчет металлической балки на прогиб: учимся составлять формулы

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

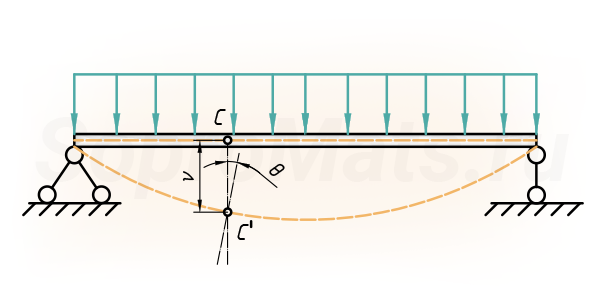
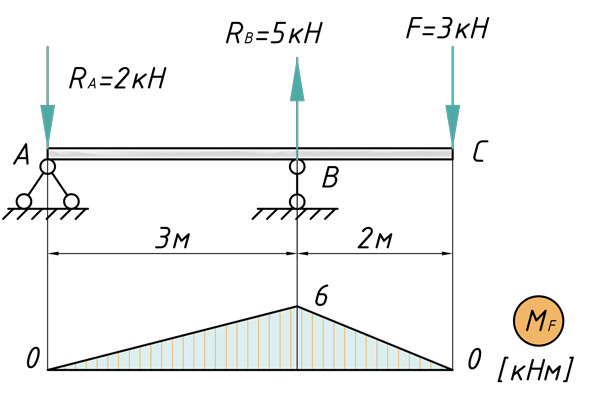
ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

• в опорах прогибы равны нулю;
• в жесткой заделке прогиб и угол поворота сечения равен нулю.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

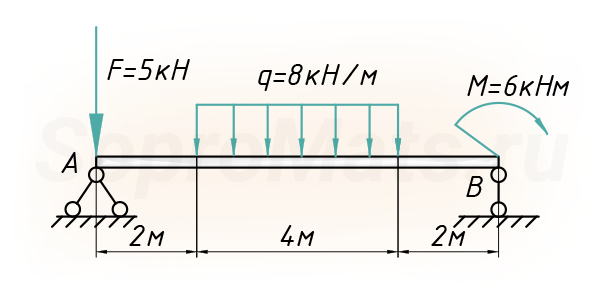
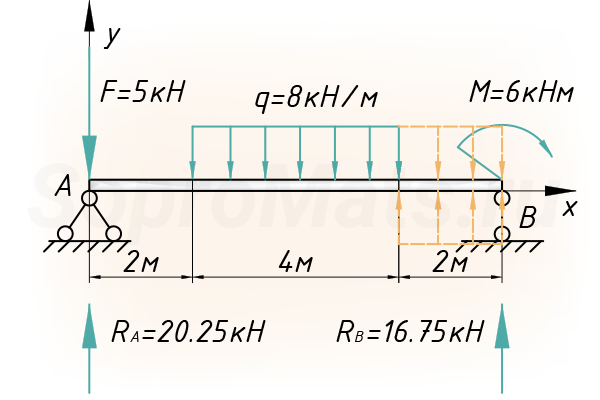
Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

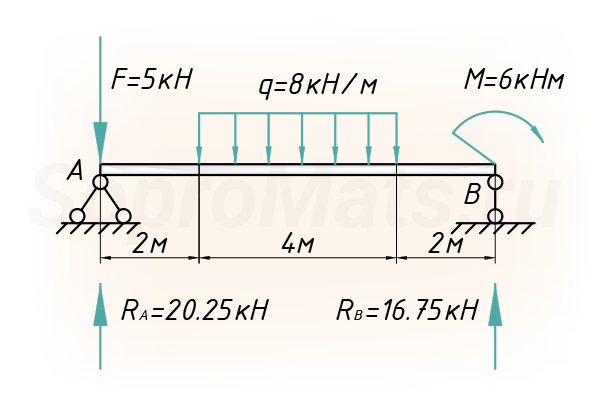
Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

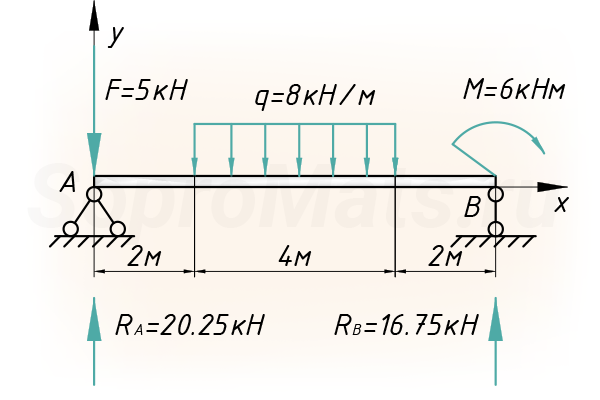
Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

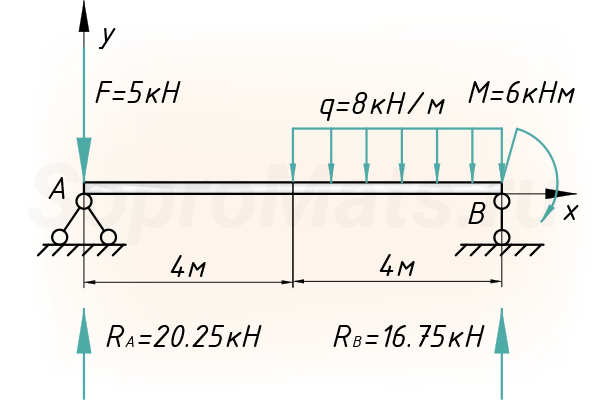
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

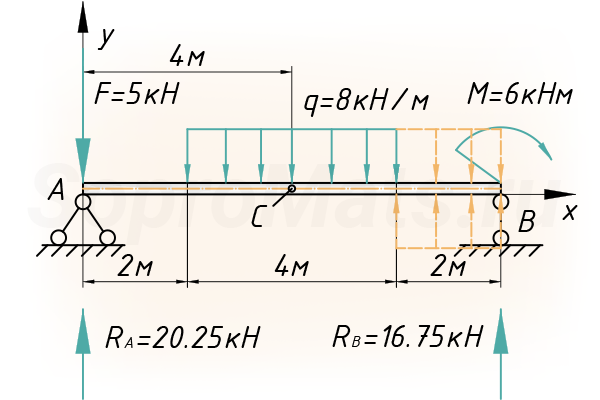
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

Записываем уравнение метода начальных параметров для сечения C:

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. Здесь есть несколько особенностей:

• Сосредоточенные силы и распределенные нагрузки, которые направленны вверх, то есть совпадают с направлением оси y, в уравнении записываются со знаком «плюс». Если они направленны наоборот, соответственно, со знаком «минус»:

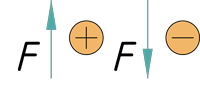
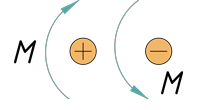
• Моменты, направленные по часовой стрелке – положительные, против часовой стрелки – отрицательные:

• Все сосредоточенные моменты нужно умножать дробь:

[ Mcdot frac < < x >^ < 2 >>< 2 >]

• Все сосредоточенные силы нужно умножать дробь:

[ Fcdot frac < < x >^ < 3 >>< 6 >]

• Начало и конец распределенных нагрузок нужно умножать на дробь:

Формулы прогибов

С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

Выражаем угол поворота:

Подставляем это значение в наше первое уравнение и находим искомое перемещение:

Вычисление прогиба

Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

[spoiler title=”источники:”]

http://ssopromat.ru/raschet-progiba-balki-metodom-nachalnyh-parametrov/

http://sopromats.ru/sopromat/raschet-progiba-balki/

[/spoiler]

6.1. Понятие об упругой
линии. Прогиб и угол поворота.
Дифференциальное уравнение упругой
линии. Условие жесткости при изгибе

Чтобы судить о работе изгибаемых балок,
недостаточно знать только напряжения,
которые возникают в сечениях балки от
заданной нагрузки. Вычисленные напряжения
позволяют проверить прочность системы.
Однако весьма прочные балки могут
оказаться непригодными к эксплуатации
из-за недостаточной жесткости. Если
балка при нагружении сильно прогибается,
то при эксплуатации сооружения, имеющего
гибкие балки, появятся затруднения и,
кроме того, могут возникнуть колебания
балки с большими амплитудами, а вместе
с тем и значительные дополнительные
напряжения.

Под жесткостью
следует понимать способность
элеменов конструкций и деталей машин
сопротивляться внешним нагрузкам без
видимых деформаций.
Расчет на жесткость заключается в оценке
упругой податливости балки под действием
приложенных нагрузок и подбор таких
размеров поперечного сечения, при
которых перемещения не будут превышать
установленных нормами пределов. Для
выполнения такого расчета необходимо
научиться вычислять перемещения сечений
балки под действием любой внешней
нагрузки.

Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.

Точка
,
лежащая на оси в сечении, отстоящем не
расстоянииот начала координат, переместится в
точку.
Обозначим перемещение произвольной
точки оси бруса в направлении осичерез,
а перемещение вдоль оси бруса – через.
Если в точкепровести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол.
Одновременно на тот же угол повернется
сечение в точке.
Таким образом, три величины
,иявляются компонентами перемещения
произвольного поперечного сечения
балки. Перемещениецентра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
.

Угол
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью.

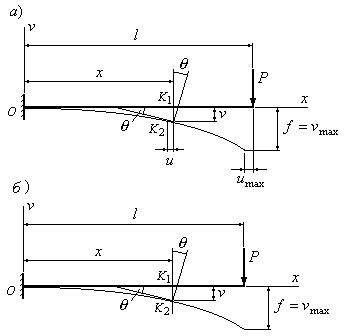
Рис.6.1

Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб
не должен превышать определенной доли
пролета:

.

Число
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величинапринимается равной 1000.

Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:

.
(6.1)

Во-вторых, горизонтальными
перемещениями
можно пренебречь, так как они существенно
меньше().
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.

Для определения полной картины деформаций
необходимо получить уравнение упругой
линии

.

Исходя из физической природы изогнутой
оси бруса, можем утверждать, что упругая
линия должна быть непрерывной и гладкой
кривой, следовательно, на протяжении
всей оси бруса должны быть непрерывны
функция и ее первая производная. Прогибы
и углы поворота и являются перемещениями
сечений балок при изгибе. Деформация
того или иного участка балки определяется
его кривизной.

При выводе формулы для нормальных
напряжений при изгибе нами была получена
связь между кривизной и изгибающим
моментом:

.
(6.2)

Из курса высшей математики известно
следующее уравнение кривизны плоской
кривой:

.
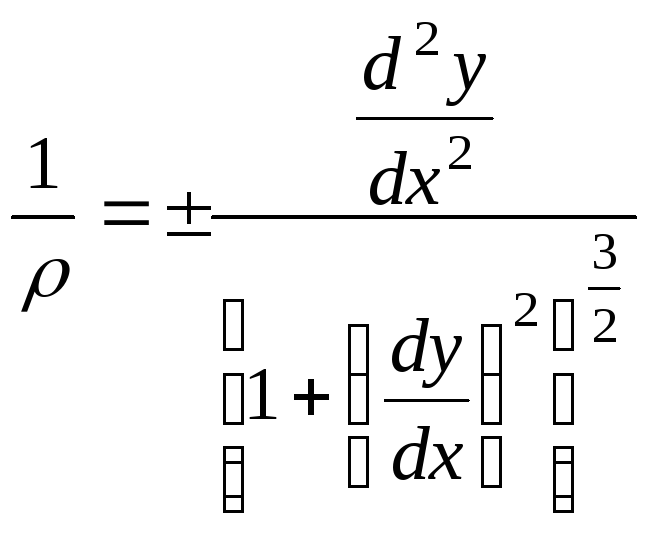(6.3)

Подставляя значение
кривизны в равенство (6.2) и заменяя
координату
прогибом,
получим точное дифференциальное
уравнение упругой линии балки:

.
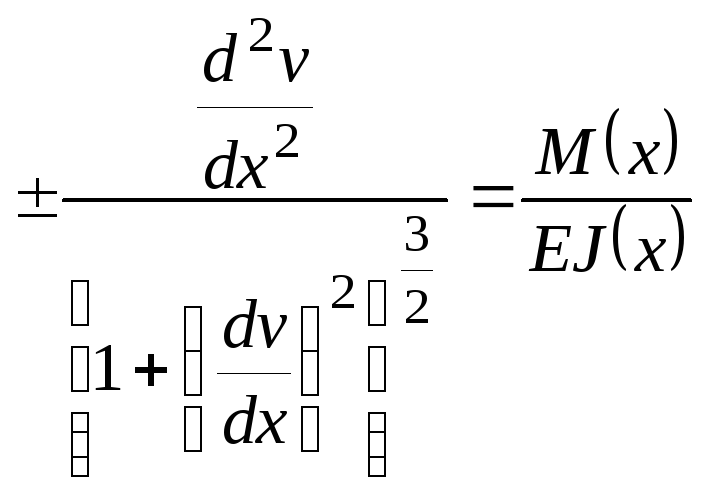(6.4)

Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона
касательной к оси будут малы, квадратом
первой производнойпо
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение

(6.5)

Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны
может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
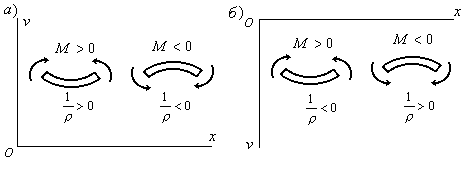
растянутые волокна. Так, например, для
случая, когда осьнаправлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.

Рис
6.2

Таким
образом, в случае, когда ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.

6.2. Метод непосредственного
интегрирования приближенного (основного)
дифференциального уравнения упругой
линии

Решая
задачу аналитическим методом, углы
поворота
и прогибывычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота:

,
(6.6)

где

постоянная интегрирования.

Интегрируя
второй раз, получим выражение для прогиба
:

,
(6.7)

где
и
постоянные интегрирования.

Для
вычисления интегралов, входящих в (6.6)
и (6.7), необходимо сначала написать
аналитические выражения для изгибающего
момента и жесткости. Постоянные
интегрирования находятся
из граничных условий,
которые зависят от условий перемещения
границ участков балки.

Рассмотрим несколько
примеров применения метода непосредственного
интегрирования приближенного уравнения
упругой линии балки.

Пример
6.1. Определить
стрелу прогиба и угол поворота сечения
В балки, изображенной на рис.6.3.

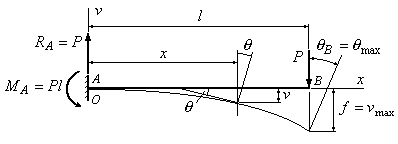
Рис.6.3

Решение:

1. Из условий
равновесия определяем опорные реакции:

;
.

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

.

4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получаем:

.
(а)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(б)

Так как в заделке прогиб и угол поворота
равны нулю, то для определения постоянных
интегрирования граничные условия имеют
вид:

при
;
при.

Из
уравнения (а) видно, что постоянная
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а),
находим.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
,
получаем.

Таким образом,
получаем следующие выражения для прогиба
и угла поворота:

,

.

Подставляя
в первое уравнение
,
найдем стрелу прогиба:

.

Подставляя
во второе уравнение
,
найдем максимальный угол поворота

.

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.

Пример
6.2. Определить
стрелу прогиба двухопорной балки и углы
поворота опорных сечений А и В (рис.6.4).

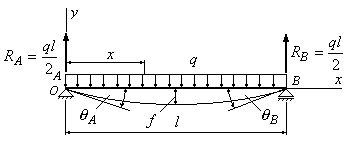
Рис.6.4

Решение:

1. Из условий
равновесия определяем опорные реакции:

.

2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.

3.
Составляем уравнение изгибающего
момента в сечении
:

.

4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Интегрируем
уравнение первый раз. Получим:

.
(в)

Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:

.
(г)

Постоянные
интегрирования найдем из граничных
условий:

при
;
при.

Подставляя
в уравнение (г)
и приравнивая прогиб нулю, получим;
подставляя в это же уравнение,
находим постоянную интегрирования:

.

Найденные значения
постоянных интегрирования подставим
в уравнения (в) и (г) и получим уравнения
углов поворота и прогибов:

;

.

Подставляя
ив первое уравнение, получим углы поворота
соответственно сечений А и В:

;

.

В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение
,
получим:

.

Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение В повернулось
против часовой стрелки.

Пример
6.3. В сколько
раз прогиб в сечении В на конце изображенной
на рис.6.5 балки, больше, чем прогиб в
сечении С
посредине
балки?

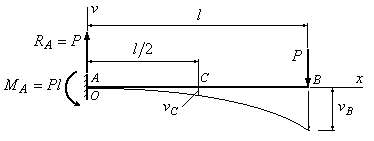
Рис.6.5

Решение:

Воспользуемся
результатами, полученными в примере
6.1. Запишем окончательное выражение для
прогиба:

и подставим в это
уравнение координаты точек С и В. Получим:

при
;

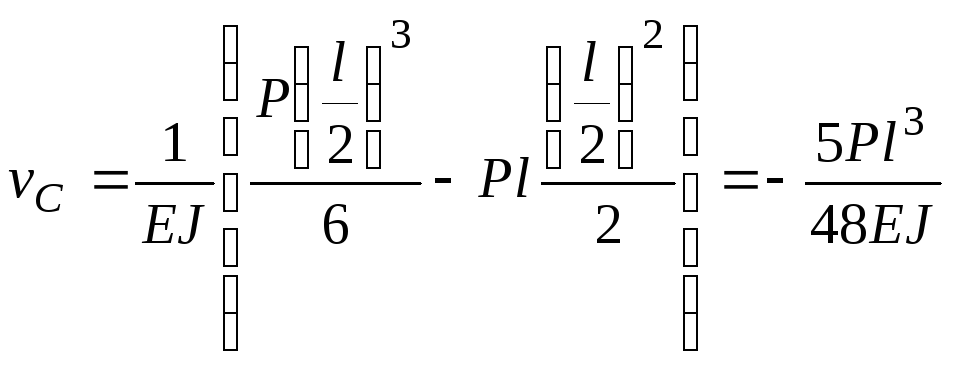при
.

Сравнивая полученные
величины прогибов, приходим к выводу,
что прогиб в сечении В больше, чем прогиб
в сечении С в 3,2 раза:

.

Пример
6.4. В сколько
раз угол
поворота сечения
А
на конце изображенной на рис.6.6 балки
больше, чем угол поворота сечения В на
расстоянии четверти пролета от левого
конца балки?

Решение:

1.
Находим реакции: ;.

2.
Выбираем начало координат
на правом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
влево.

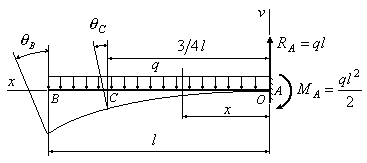
Рис.6.6

3.
Записываем выражение для изгибающего
момента в сечении
:

.

4. Составляем приближенное дифференциальное
уравнение упругой линии балки:

.

Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.

5. Принимаем жесткость балки постоянной.
Интегрируем дифференциальное уравнение.
Получаем:

.(д)

Постоянную интегрирования
в уравнении (д) найдем из условия, что
приугол поворота в сечении А равен нулю.
Подставим в уравнение (д)и приравняем нулю угол поворота сечения
А. Получим.
Тогда окончательно уравнение для угла
поворота принимает вид:

.(е)

6.
Подставляем в уравнение (е) координату
,
получим угол поворота в сечении С:

.

7.
Подставляем в уравнение (е) координату
.
Получим угол поворота в сечении В:

.

8. Сравнивая углы
поворота в сечениях В и С, получим:

.

Таким образом,
угол поворота в сечении В в 1,016 раза
больше, чем угол поворота в сечении С.

Пример
6.5.
Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна
кНм².

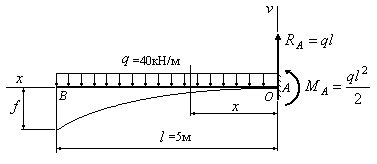
Рис.6.7

Решение:

Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении
:

.
(ж)

Постоянные
интегрирования в уравнении (ж) получим,
воспользовавшись граничными усорвиями
закрепления балки, в соответствии с
которыми прогиб и угол поворота в жесткой
заделке равны нулю:

при
и.

Подставляя
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:;.
Тогда выражение для прогиба принимает
вид:

.

Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба (),
находим:

ммм.

Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Виды перемещений при изгибе

Упругая линия балки – ось балки после деформации.

Прогиб балки $y$ – поступательное перемещение центра тяжести в поперечном направлении балки. Прогиб вверх считаем положительным, вниз –’емким.

Уравнение упругой линии – математическая запись зависимости $y(x)$ (прогиба по длине балки).

Стрела прогиба $f = {y_{max }}$ – максимальное по длине значение прогиба балки.

Угол поворота сечения $varphi $ – угол, на который поворачивается сечение в процессе деформирования балки. Угол поворота считаем положительным, если сечение поворачивается против часовой стрелки, и наоборот.

Угол поворота сечения равен углу наклона упругой линии. Таким образом, функция изменения угла поворота по длине балки равна первой производной от функции прогибов $varphi (x) = y'(x)$.

Таким образом, при изгибе рассматриваем два вида перемещений – прогиб и угол поворота сечения.

Цель определения перемещений

Перемещение в стержневых системах (в частности в балках) определяются для обеспечения условий жесткости (прогибы ограничиваются строительными нормами).

Кроме этого, определение перемещений необходимо для расчета прочности статически невыдающихся систем.

Дифференциальное уравнение упругой линии (изогнутой оси) балки

На данном этапе необходимо установить зависимость перемещений в балке от внешних нагрузок, способа закрепления, размеров балки и материала. Для полного решения задачи необходимо получить функцию прогибов $y(x)$ по всей длине балки. Вполне очевидно, что перемещения в балке зависят от деформаций каждого сечения. Ранее нами была получена зависимость кривизны сечения балки от изгибающего момента, действующего в этом сечении.

$frac{1}{rho } = frac{M}{{EI}}$.

Кривизна линии определяется ее уравнением $y(x)$ так

$frac{1}{rho } = frac{{y}}{{{{left( {1 + {{left( {y’} right)}^2}} right)}^{3/2}}}}$ ,

где $y’$ и $y$ – соответственно, первая и вторая производная от функции прогибов с координатой x.

С практической точки зрения эту запись можно упростить. На самом деле $y’ = varphi $ – угол поворота сечения в реальных конструкциях не может быть большим, как правило не больше 1град = 0,017рад. Тогда $1 + {left( {y’} right)^2} = 1 + {0.017^2} = 1.000289 approx 1$, то есть можно считать, что $frac{1}{rho } = y” = frac{{{d^2}y}}{{d{x^2}}}$. Таким образом, мы получили уравнение упругой линии балки (дифференциальное уравнение изогнутой оси балки). Это уравнение впервые получено Эйлером.

$frac{{{d^2}y}}{{d{x^2}}} = frac{{M(x)}}{{EI}}.$

Получена дифференциальная зависимость показывает взаимосвязи между перемещениями и внутренними усилиями в балках. Учитывая дифференциальную зависимость между поперечной силой, изгибающим моментом и поперечной нагрузкой, покажем содержание производных от функции прогибов.

$y(x)$ – функция прогибов;

$y'(x) = varphi (x)$ – функция углов поворота;

$EI cdot y”(x) = M(x)$ – функция изменения изгибающего момента;

$EI cdot y”‘(x) = M'(x) = Q(x)$ – функция изменения поперечной силы;

$EI cdot {y^{IV}}(x) = M”(x) = q(x)$ – функция изменения поперечной нагрузки.