Задача. Для заданного стального бруса d=50мм (материал – сталь Ст3) построить эпюры крутящих моментов, углов поворота поперечных сечений. Проверить прочность бруса, если допускаемое касательное напряжение [τ]=30МПа. Подобрать для бруса кольцевое сечение при  . Сравнить сечения по расходу материала.
. Сравнить сечения по расходу материала.
 1.Расставляем сечения на характерных участках. Начинаем расчет от свободного конца бруса, рассматривая правую часть и отбрасывая оставшуюся левую часть с заделкой. Каждое сечение рассматриваем отдельно, определяя в нем значение крутящего момента.
1.Расставляем сечения на характерных участках. Начинаем расчет от свободного конца бруса, рассматривая правую часть и отбрасывая оставшуюся левую часть с заделкой. Каждое сечение рассматриваем отдельно, определяя в нем значение крутящего момента.


Строим эпюру МК

2.Строим эпюру углов поворота сечений. Углы поворота сечений определяем по формуле ![]()
Расчет ведем по сечениям от неподвижного конца – стены А, в которой угол поворота равен нулю φА=0. В формуле обязательно следует учитывать знаки крутящих моментов.
Модуль сдвига для Ст3 G = 0,8·105 МПа = 0,8·108 кПа.
Определим полярный момент инерции для круглого сечения:

Вычисляем углы поворота сечений — от стены А.

Если требуется перейти к градусной мере, то:

Далее вычисляем все последующие углы поворота, учитывая ранее найденные:
 Строим эпюру φ
Строим эпюру φ

3.Проверим прочность бруса по формуле 
Максимальный крутящий момент с эпюры МК = 0,75 кНм.
Определим полярный момент сопротивления сечения:
![]()
Тогда –прочность обеспечена.
–прочность обеспечена.
4.Подбираем кольцевое сечение для вала с  .
.
Наружный диаметр кольца определим по формуле проектного расчета для кольцевого сечения:

Тогда d = 0,8 · 60 = 48 мм.
Проверим прочность подобранного сечения. Полярный момент сопротивления для кольца:
 Тогда
Тогда – прочность обеспечена.
– прочность обеспечена.
5. Сравним варианты – круглое и кольцевое – по расходу материала



В задаче площадь круглого вала А = 19,6 см2, а у кольцевого сечения (полого) А = 10,7 см2, что позволяет говорить об экономии материала почти в два раза. Т.о. брус (вал) кольцевого сечения экономичнее равнопрочного сплошного.
Объясняется это эпюрой касательных напряжений в сплошном брусе.
Для вала определить диаметр, построить эпюры крутящих моментов и углов закручивания.
1) Определяем величины внутренних крутящих моментов M. Для этого разбиваем стержень на участки (I, II, III, IV) и производим расчёт M со свободного конца стержня. Крутящий момент M в сечении равен алгебраической сумме моментов, действующих на стержень с одной стороны (справа) от рассматриваемого сечения.
Расчёт M соответственно по участкам IV, III, II, I:
MIV=M4;
MIII=M4 – M3;
MII = M4 – M3 – M2;
MI = M4 – M3 – M2+M1.
Зная числовые значения крутящих моментов M, строится эпюра M, при этом положительные значения M откладываются вверх, а отрицательные – вниз от горизонтальной линии. 
2) Определяем диаметр стержня из условия прочности: Выразим
Выразим ![]() –полярный момент сопротивления при кручении круглого стержня через диаметр:
–полярный момент сопротивления при кручении круглого стержня через диаметр:![]() тогда получим:
тогда получим: 
![]() берётся из эпюры M по абсолютному значению. Диаметр стержня d округляется до большей величины.
берётся из эпюры M по абсолютному значению. Диаметр стержня d округляется до большей величины.
3) Производим расчет жесткости вала при кручении![]() , где
, где ![]() – модуль сдвига, а
– модуль сдвига, а ![]() (см4) – полярный момент инерции сечения.
(см4) – полярный момент инерции сечения.
4) Производим расчет ![]() – углов закручивания концов участков стержня, начиная от закреплённого конца стержня, где
– углов закручивания концов участков стержня, начиная от закреплённого конца стержня, где ![]() ,(рад):
,(рад): Значения крутящих моментов на участках берутся из эпюры крутящих моментов с учётом их знака. Получив численные значения
Значения крутящих моментов на участках берутся из эпюры крутящих моментов с учётом их знака. Получив численные значения ![]() , строят эпюру
, строят эпюру ![]() . Примерная эпюра
. Примерная эпюра ![]() показана на рисунке.
показана на рисунке.
Ступенчатый стержень нагружен крутящим моментом Т .При каком отношении ![]() выполняется условие одинаковой прочности по всей длине стержня, если
выполняется условие одинаковой прочности по всей длине стержня, если ![]()

Условие одинаковой прочности на участках будет выполнено в том случае ,если касательные напряжения будут одинаковы. 
Определим касательные напряжения, обозначив крутящий момент в левой стене как ![]() , а в правой как
, а в правой как ![]() :
:
 Определим полярные моменты сопротивления сечений :
Определим полярные моменты сопротивления сечений :![]() Тогда найдем соотношение между
Тогда найдем соотношение между ![]() и
и ![]() :
:
 (1)
(1)
Теперь составим уравнение деформаций – углов поворота. Начнем от правой стены В, в которой ![]() . Внутренний крутящий момент во втором сечении будет равен
. Внутренний крутящий момент во втором сечении будет равен ![]() , а крутящий момент в первом сечении будет равен
, а крутящий момент в первом сечении будет равен ![]() . Тогда уравнение углов поворота:
. Тогда уравнение углов поворота: (2)
(2)
Полярные моменты инерции:![]() Подставим эти значения в уравнение (2) и найдем соотношение между
Подставим эти значения в уравнение (2) и найдем соотношение между ![]() и
и ![]() :
:
 (3)
(3)
Составим уравнение статики для заданной схемы:![]() Тогда:
Тогда: (4)
(4)
Теперь, решая (4) , (3) и (1), получим отношение ![]() . Задача решена.
. Задача решена.
Для стального вала, нагруженного внешними крутящими моментами, построить эпюры внутренних крутящих моментов, определить размеры поперечного сечения в виде кольца (d/D=0,85) из условий прочности и жесткости, построить эпюры максимальных касательных напряжений, абсолютных и относительных углов поворота поперечных сечений. 
Дано: 
Определим внутренние крутящие моменты. Расчет внутренних крутящих моментов проводится с помощью метода сечений.
Участок LK: МL= М4 = 5 кНм; МК=М4=5кНм.
Участок KD: МК= М4 — M3 = 5-8 =-3кНм; MD= М4 -M3=5-8=-3кНм;
Участок DC: MD= М4 -M3+M2=5-8+6=3кНм; MC= М4 -M3+M2=5-8+6=3кНм;
Участок CB: MC= М4 -M3+M2-M1=5 -8+6-4=-1кНм; MB= М4 -M3+M2-M1=5 -8+6-4=-1кНм.
Покажем эпюру крутящих моментов на рис.б.


Определяем размеры поперечного сечения вала из условия прочности и жесткости: , где полярный момент сопротивления сечения и полярный момент инерции сечения равны:
, где полярный момент сопротивления сечения и полярный момент инерции сечения равны: Максимальный внутренний крутящий момент:
Максимальный внутренний крутящий момент:![]()
Тогда из условия прочности:

А из условия жесткости: Окончательно принимаем D=90мм.
Окончательно принимаем D=90мм.
Для подобранного сечения вала его геометрические характеристики:
Рассчитаем касательные напряжения для участков:
Построим эпюру касательных напряжений на рис.в.
Расчет относительных углов поворота на участках:
Сначала определим жесткость сечения вала при кручении:
Тогда:
Эпюра θ показана на рис. г.
Определение угловых перемещений характерных сечений (идем от опоры В, в которой угол поворота равен 0):
Эпюра φ представлена на рис.д.
Стальные стержни 1 и 2 нагреваются на ![]() . Площадь стержней А.
. Площадь стержней А.
Определить максимальные напряжения.
При нагреве стержней на ![]() возникнут температурные напряжения.
возникнут температурные напряжения.
Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения ![]() и разности температур
и разности температур ![]() .
.
![]()
Эти напряжения создадут усилия:
![]() Тогда крутящий момент:
Тогда крутящий момент:![]()
Касательные напряжения:

Следует помнить, что при нагреве стержней в них возникают сжимающие напряжения, а при охлаждении – растягивающие. Эти напряжения, суммируясь с напряжениями от силовых факторов, могут значительно превышать допускаемые. Это обстоятельство следует учитывать при проектировании элементов конструкций.
К стальному валу приложены три известных момента: ![]()
Требуется: 1) установить, при каком значении Х угол поворота правого крайнего сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов поворота; 5) найти наибольший относительный угол закручивания (в градусах на 1м длины). ![]()
Решение: Обозначим границы участков русскими буквами А,……,Д.

I.Записываем условие, что угол поворота крайнего правого сечения (Д) вала равен нулю – исходя из условий задачи.![]()
Данный угол поворота является суммой углов поворота вала на каждом участке:
![]()
Угол поворота на участке определяется по формуле:
 , где М к – крутящий момент на данном участке, l — длина участка,
, где М к – крутящий момент на данном участке, l — длина участка,
G — модуль сдвига , ![]() – для стали
– для стали
![]() – полярный момент инерции
– полярный момент инерции 
Таким образом,  , и с учетом условия задачи:
, и с учетом условия задачи:

Так как вал имеет постоянное поперечное сечение, то
 (1)
(1)
Определяем внутренние крутящие моменты на участках методом сечений. Идем от свободного конца вала, на каждом участке мысленно проводим сечение и рассматриваем равновесие всегда правой отсеченной части:

Подставляем найденные значения моментов в уравнение (1) :

2. Строим эпюру крутящих моментов. Для этого подставляем в выражения для моментов Мк найденные значения Х.

Полученные значения откладываем в виде ординат на эпюре

3.Определяем диаметр вала из условия прочности:
 , где
, где![]() –максимальное касательное напряжение,
–максимальное касательное напряжение,
 – максимальный крутящий момент (берется с эпюры Мкр по модулю),
– максимальный крутящий момент (берется с эпюры Мкр по модулю),
 – полярный момент сопротивления сечения
– полярный момент сопротивления сечения
[τ]=80 МПа — допускаемое касательное напряжение
Определяем диаметр:
Принимаем диаметр вала d=45 мм=4,5 см
4. Построение эпюры углов поворота начинаем от опоры и строим нарастающим итогом. Предварительно посчитаем жесткость вала:

Угол поворота в левой опоре равен нулю, поскольку в заделке поворота быть не может: ![]()

В последней точке угол поворота должен получиться равным нулю (по условию задачи), таким он и получился. Строим эпюру углов поворота.
5. Наибольший относительный угол закручивания определим по формуле:
 Полученный результат переведем в градусы на метр длины:
Полученный результат переведем в градусы на метр длины: 
Пусть:М1=5кНм, М2=10кНм, ℓ=1м, [τ]=100МПа, G=8∙1010Па
Требуется: 1) Построить эпюру крутящих моментов и подобрать размеры поперечных сечений заданной формы, соблюдая следующие соотношения между ними:

2) Построить эпюру углов поворота.

Сначала составляем уравнение статики для всего бруса:
 (1)
(1)
Здесь два неизвестных, следовательно, требуется еще одно уравнение. Его получим, если сформулируем условие совместности деформаций всех трех участков бруса. Оно заключается в том, что поворот правого опорного сечения относительно левого опорного сечения для рассматриваемого бруса невозможен, поскольку оба его концы жестко защемлены:
φI+ φII+ φIII=0.
Учитывая, что

получаем:
 (2)
(2)
Сократим на ![]() , тогда будет:
, тогда будет:
 (2′)
(2′)
Выразим моменты инерции сечений разных форм с учетом заданных соотношений размеров:

При h/b=2: β=0,229, и тогда IкIII= β∙h∙b3=0,229∙(2b)∙b3=0,458∙ b4=0,458∙ c4.
Итак, все моменты инерции выражены через один параметр с, что позволит довести до числа решение уравнения (2′):

или после сокращения на с4:
 (2′′)
(2′′)
С помощью метода сечений выразим неизвестные крутящие моменты через один из реактивных опорных моментов, например, через МА:
 (а)
(а)
 (б)
(б)
 (в)
(в)
С учетом (а), (б) и (в) уравнение (2′′), будет:

откуда находим значение МА:

— 13,892МА=3,33.
МА=-0,24кНм
Тогда из (а), (б) и (в) найдем:

Эти результаты показаны в виде эпюры крутящих моментов.
Подбор размеров сечений производится по условиям прочности:
— на первом участке

Для круглого сечения

При заданном соотношении d=c:

Тогда

— на втором участке

Для кольцевого сечения

Здесь мы должны учесть соотношения размеров, при которых и найдены внутренние усилия, то – есть
![]()
тогда:

— на третьем участке

Для прямоугольного сечения ![]() . При соотношениях
. При соотношениях 
По таблице α=0,246. И тогда Wк=2∙0,246∙с3.
Из условия прочности

Из трех требуемых значений «с» (0,023м, 0,04м и 0,046м) принимаем наибольшее с=0,046м и тогда проектные значения размеров сечений на разных участках должны быть
— на первом участке: круглое сечение диаметром d=0,046м,
у которого 
— на втором участке: кольцевое сечение с внутренним диаметром d=0,046м, а внешним  у которого
у которого 
— на третьем участке: прямоугольное сечение шириной b=c=0,046м
и высотой h=2b=2∙0,046=0,092 м,
у которого Iк=β∙h∙b3=0,229∙0,092∙0,0463=205∙10-8м4.
2. Построение эпюры углов поворота.
Для этого вычисляются углы поворота сечений, расположенных на границах участков бруса (эти сечения на схеме обозначены цифрами в кружочках), они откладываются в виде ординат, вершины которых соединяются прямыми линиями. Так:
α0=0, поскольку крайнее левое сечение жестко защемлено и поворачиваться вокруг продольной оси z не может,

Равенство нулю угла поворота крайнего правого сечения, тоже жестко защемленного, служит контролем правильности всего решения задачи.

Уравнение статики для всего бруса:
ΣМ(z) = МА— М1 — М2 + МВ= 0. (1)
В этом уравнении два неизвестных (это реактивные моменты в опорах МА и МВ). Следовательно, задача один раз статически неопределима, и для ее решения необходимо составить дополнительное уравнение, выражающее факт совместности деформаций всех участков бруса.
Здесь можно рассуждать следующим образом: если удалить одну из опор, то брус станет статически определимым
Теперь крайнее правое сечение получило возможность поворачиваться. Но в заданной системе этот поворот невозможен. Поэтому величину МВ в удаленной опоре следует подобрать так, чтобы угол поворота опорного сечения равнялся нулю:
αВ=0 – это условие деформации.
Раскрывая его, будем иметь:
αВ= αА+φI+ φII+ φIII=0+φI+ φII+ φIII=0. (а)

Тогда условие совместности деформаций (а) превращается в уравнение совместности деформаций:
 (2)
(2)
В этом уравнении три неизвестных крутящих момента (по количеству участков бруса). Для их определения выразим крутящие моменты через заданные внешние скручивающие моменты М1, М2 и реактивные моменты, используя метод сечений. Так в любом сечении первого участка:

( (b)
(b)
Далее, в любом сечении второго участка

 ©
©
Наконец, в любом сечении третьего участка:

 (d)
(d)
Подставляя (b), © и (d) в уравнение (2), будем иметь:
 (2′)
(2′)
В этом уравнении содержится одно-единственное неизвестное: это реактивный момент в левой опоре МА. Определив его из решения уравнения (2′), обратной подстановкой в формулы (b), © и (d) определим численные значения крутящих моментов ![]() , Таким образом статическая неопределимость задачи будет раскрыта.
, Таким образом статическая неопределимость задачи будет раскрыта.
Зная крутящие моменты, далее можно решить любую задачу прочности и жесткости бруса.
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ
:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:

Угол закручивания

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение», «Таблицы» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Значения коэффициента γ<1 берутся из той же таблицы, что и значения α и β.
Угол поворота вала Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Дизайн машины ↺ | |
| Дизайн машины | Проектирование элементов машин ↺ | |
| Проектирование элементов машин | Конструкция валов ↺ | |
| Конструкция валов | Торсионная жесткость ↺ |
|
✖Крутящий момент в валу — это реакция, возникающая в элементе конструктивного вала, когда к элементу прилагается внешняя сила или момент, вызывающий скручивание элемента.ⓘ Крутящий момент на валу [Mtshaft] |
+10% -10% |
||
|
✖Длина вала по жесткости на кручение — это длина вала, рассчитанная на основе жесткости на кручение.ⓘ Длина вала от жесткости на кручение [L] |
+10% -10% |
||
|
✖Модуль жесткости вала — это коэффициент упругости при приложении поперечной силы, приводящей к поперечной деформации. Это дает нам меру жесткости вала.ⓘ Модуль жесткости вала [G] |
+10% -10% |
||
|
✖Диаметр вала по жесткости на кручение — это диаметр внешней поверхности вала, рассчитанный на основе жесткости на кручение.ⓘ Диаметр вала от жесткости на кручение [d] |
+10% -10% |
|
✖Угол поворота вала — это угол, на который поворачивается закрепленный конец вала по отношению к свободному концу.ⓘ Угол поворота вала [θ] |
⎘ копия |
Угол поворота вала Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Крутящий момент на валу: 330000 Ньютон Миллиметр –> 330 Ньютон-метр (Проверьте преобразование здесь)
Длина вала от жесткости на кручение: 450 Миллиметр –> 0.45 метр (Проверьте преобразование здесь)
Модуль жесткости вала: 90000 Ньютон на квадратный миллиметр –> 90000000000 Паскаль (Проверьте преобразование здесь)
Диаметр вала от жесткости на кручение: 43.5 Миллиметр –> 0.0435 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.269116151488221 Радиан –>15.4192196790813 степень (Проверьте преобразование здесь)
5 Торсионная жесткость Калькуляторы
Угол поворота вала формула
Угол поворота вала = 584*Крутящий момент на валу*Длина вала от жесткости на кручение/(Модуль жесткости вала*Диаметр вала от жесткости на кручение^4)
θ = 584*Mtshaft*L/(G*d^4)
Определить угол закрутки?
Для вала, находящегося под действием крутильной нагрузки, угол, на который неподвижный конец вала вращается относительно свободного конца, называется углом кручения. По мере увеличения крутящего момента внешняя область вала ведет себя как пластик, в то время как внутренний сердечник остается линейно упругим.

Подборка формул для расчета валов и брусьев на кручение и решения задач сопротивления материалов по расчету внутренних моментов, касательных напряжений, деформаций и углов закручивания при кручении.
Обозначения:
τ — касательные напряжения,
T – внутренний крутящий момент,
Ip – полярный момент инерции сечения вала,
Wp – полярный момент сопротивления сечения,
[τ] – допустимое напряжение,
G – модуль упругости II рода (модуль сдвига),
ρ — расстояние от центра сечения до рассматриваемой точки,
D – внешний диаметр вала,
d – внутренний диаметр вала кольцевого сечения.
Закон Гука при кручении (чистом сдвиге)
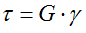
Расчет касательных напряжений в произвольной точке сечения вала
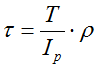
Условие прочности при кручении (проверочный расчет)
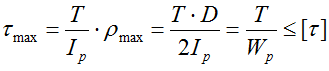
Формулы полярных моментов инерции и сопротивления
Формулы для подбора диаметра вала по условию прочности
Абсолютные деформации (угол закручивания участков вала)
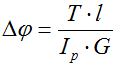
Перемещение (угол поворота) сечений.
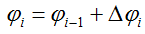
Здесь: φi — угол поворота рассматриваемого сечения,
φi-1 — перемещение предыдущего сечения,
Δφi — деформация участка между указанными сечениями.
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
Кручение возникает в элементах конструкций при таких воздействиях, которые можно схематизировать только скручивающими моментами. Такой брус в технике называют валом. Обычно эти элементы имеют вид прямого бруса как постоянного, так и переменного сечения. Например, испытывают кручение валы механических передач, несущие зубчатые колёса и другие детали передач; коренные валы машин, которые несут рабочие органы машин (колёса турбин, кривошипы и др.); валы двигателей и станков; оси автомобилей, моторных вагонов и локомотивов. Также подвергаются скручиванию и элементы пространственных конструкций (в частности, пространственных рам).
При составлении схем расчёта вала необходимо учитывать вид внешнего воздействия и способ присоединения (или опирания). Чаще способ крепления валов такой, что препятствует как линейному перемещению, так и угловому (т. е. повороту опорного сечения), поэтому на схеме вала изображается жёсткая заделка (защемление). По количеству защемлений схемы валов могут быть статически определимыми (вал с одной заделкой) и статически неопределимыми (вал с двумя и более заделками).
Вданном пособии приведены расчёты круглых ступенчатых валов, имеющих одну или две жёсткие заделки при действии сосредоточенных и распределённых моментов; выполнены расчёты как на прочность, так и на жёсткость. Рассматривается решение следующих задач:
Задача 12. Проектный расчёт ступенчатого вала.
Задача 13. Проектный расчёт ступенчатого статически неопределимого вала.
Задача 14. Проверочный расчёт ступенчатого вала.
Задача 15. Проверочный расчёт ступенчатого статически неопределимого вала.
Вкаждой из этих задач требуется выполнить расчёт на прочность, в котором оценивается сопротивление вала внешним воздействиям. От воздействия внешних скручивающих моментов в сечениях вала возникает только крутящий момент, который вычисляется, как и любое внутреннее усилие, методом сечений (с помощью правила РОЗУ: Разрезать, Отбросить, Заменить, Уравновесить). Для вычисления крутящего момента составляют уравнение равновесия отсечённой части вала в виде суммы мо-
84
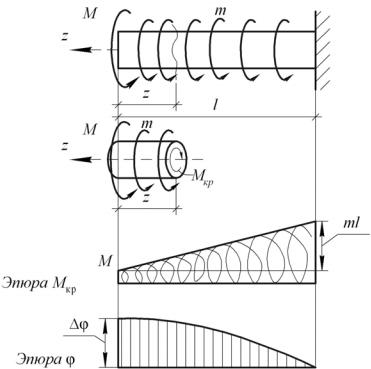
ментов всех внешних нагрузок и внутреннего крутящего момента относительно оси вала:
Для моментов используем известные общепринятые правила знаков: при взгляде на сечение внешние моменты, приложенные к рассматриваемой отсечённой части, считаем положительными, если они направлены против хода часовой стрелки, и положительный внутренний крутящий момент Мкр – по часовой стрелке. Таким образом, внешние и внутренние моменты действует навстречу и компенсируют друг друга. Положительные направления моментов показаны на рис. 3.1, а, на котором изображена схема вала в общем виде. На схеме сосредоточенный момент М приложен в начале вала, а по всему валу действует распределённый момент интенсивности m.
Уравнение равновесия (3.1) для отсечённой части вала принимает вид (рис. 3.1, б):
|
Mкр mz M 0 . |
|
|
Отсюда получаем формулу крутящего момента |
|
|
Mкр M m z . |
(3.2) |
а
б
в
г
Рис. 3.1
85
Как видно, крутящий момент Мкр в сечении равен алгебраической сумме моментов относительно оси z всех внешних моментов, действующих по одну стороны от рассматриваемого сечения. Подтверждается закономерность: положительные внешние моменты создают положительный
внутренний крутящий момент. Вычислим значения Mкр в начале участка (при z = 0) и в конце участка (при z = l). Получим Mкр(0) M и Mкр(l) M ml . Отложив полученные значения, построим эпюру Мкр
(рис. 3.1, в), которая будет нарастающей от свободного края по линейному закону. Подставляя в (3.2) цифровые значения внешних моментов реального вала, можно получить для него соответствующие значения момента Мкр. При вычислении момента Мкр рекомендуем следующие методические приёмы:
1.Крутящий момент в сечении лучше брать положительного направления (по часовой стрелке), тогда получаем его значение с истинным знаком.
2.Для вала с заделкой крутящий момент проще вычислять, рассматривая отсечённую часть со стороны свободного края, тогда не обязательно определение опорного момента в заделке.
По формуле крутящего момента (3.2) хорошо прослеживается влияние сосредоточенного и распределённого моментов на значение момента
Мкр, поэтому при изображении эпюры Мкр необходимо помнить: вопервых, на участке, где нет распределённого момента ( m 0 ), крутящий
момент Mкр const , и на эпюре Mкр будет прямая, параллельная оси; во-
вторых, на участке с распределённым моментом (m ≠ 0) крутящий момент Mкр изменяется линейно, и на эпюре Mкр – наклонная прямая, причём при
m > 0 крутящий момент растёт, при m < 0 крутящий момент уменьшается. Значения моментов Mкр необходимы для выполнения дальнейших расчётов
вала на прочность и на жёсткость.
Так как работа элементов деталей машин и механизмов на кручение допускается в пределах упругих деформаций, то для расчёта вала на прочность используют условие прочности по допускаемым напряжениям, которое при кручении имеет вид
где max модуль наибольшего касательного напряжения в сечении вала,
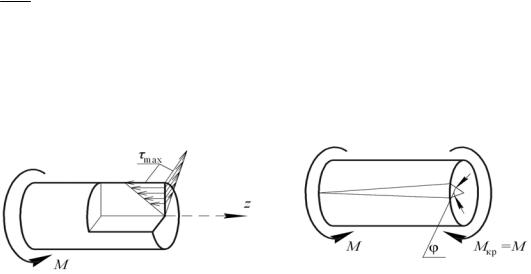
для вала круглого сечения max возникает в точках сечения у поверхности вала (рис. 3.2, а) и определяют по формуле
|
τmax |
Мкр |
, |
(3.4) |
|
Wρ |
86
в которой Мкр крутящий момент в рассматриваемом сечении;
Wρ πd3 (1 c4 ) – полярный момент сопротивления круглого сечения с со-
16
отношением внутреннего диаметра к наружному, равным с; τ допус-
каемое напряжение для материала вала.
Согласно условию прочности напряжения max не должны превышать допускаемого напряжения τ .
Рис. 3.2
В задачах КР и РГЗ рассматриваются ступенчатые круглые валы, имеющие несколько грузовых участков разного диаметра и различного характера нагрузки, поэтому условие прочности (3.3) записываем в виде
|
Mкр |
||||||
|
τ |
[τ]. |
(3.5) |
||||
|
W |
||||||
|
max |
||||||
|
ρ |
max |
Сечение вала, в котором касательные напряжения max принимает наибольшее по модулю значение, является опасным. Условие прочности (3.5) позволяет выполнять три вида расчётов:
проверочный (проверка прочности вала);
проектный (назначение диаметра вала);
определение несущей способности (вычисление допускаемого значения внешних моментов).
В рассмотренных ниже задачах выполняются первые два вида расчётов.
При работе машин и сооружений сечения валов получают угловую деформацию (рис. 3.2, б) − угол поворота сечения φ (или угол закручивания вала), который не должен превышать определённого значения, поэтому условие жёсткости вала имеет основополагающее значение для его успешной работы. Ввиду этого в задачах на кручение обязательна проверка жёсткости вала по условию жёсткости, которое записывают в виде двух выражений:
87

(1 c4 ).
где θmax и φ max – наибольшие по модулю значения соответственно относительного и абсолютного углов закручивания вала; θ и φ – значения допускаемых относительного и абсолютного углов закручивания вала. Значение θmax для ступенчатого вала определяется как
|
Mкр |
||||||
|
θ |
. |
(3.7) |
||||
|
max |
GI |
|||||
|
ρ max |
При вычислениях необходимо помнить, что при расчёте в системе СИ получаем абсолютный угол закручивания φ в радианах, а относитель-
ный θ − в рад/м. Величина φ max выбирается по эпюре φ, которая обяза-
тельно выполняется при проверке жёсткости вала. Сначала вычисляют углы закручивания участков вала по формуле
l M
φ кр d z, (3.8)
0 GIρ
где l – длина участка вала; G – модуль упругости второго рода или модуль сдвига, для стали G = 0,8·105 МПа; Iρ – полярный момент инерции кругло-
го сечения, Iρ πd 4
32
Если крутящий момент на рассматриваемом участке постоянный, то
угол закручивания участка Δφ Mкр l . Как видно, угол закручивания за-
GI
висит обратно пропорционально от значения GIρ , которое поэтому назы-
вают жёсткостью сечения при кручении.
Из-за угловых деформаций отдельных участков вала происходит реальный поворот сечения на угол φ (рис. 3.2, б), который для вала называют углом закручивания вала, он является суммой угловых деформаций Δφ предшествующих участков. Поэтому запишем угол поворота сечения в виде
|
l |
i |
||
|
φi = φi–1 +Δφi = φi–1 + i |
M кр |
d z . |
(3.9) |
|
i |
|||
|
0 |
GIρ |
Поясним вычисление на нашем примере (рис. 3.1). Угол закручивания заделки φА равен 0, а сечение свободного края вала повернулось на угол φ, который найдём по формуле
88

|
l |
M |
кр |
1 |
z |
2 |
l |
1 |
ml |
2 |
||||||||||
|
φ= φA φ 0 |
0 |
dz |
Mz m |
Ml |
. |
(3.10) |
|||||||||||||
|
2 |
|||||||||||||||||||
|
GIρ |
GIρ |
0 |
GIρ |
2 |
|||||||||||||||
Видно, что при наличии распределённого момента для угла φ име-
ем функцию 2-го порядка по отношению к переменной z, значит, величина угла изменяется вдоль вала по квадратичной зависимости от z (по квадратичной параболе). Тогда эпюра φ будет криволинейной, и нужно правильно изобразить форму кривой. Если нет распределённого момента, эпюра φ будет наклонной прямой. Чтобы уточнить форму кривизны квадратичной параболы, нужно знать угол наклона касательной к получаемой кривой, который равен производной по z от функции угла φ, т. е.
tgα dφ Mкр M mz . dz GIρ GIρ
Как видно из последнего выражения, закон изменения наклона касательной к кривой повторяет закон изменения момента Мкр, поэтому эпюра Мкр всегда позволяет определить наклон кривой φ: в рассматриваемом примере (рис. 3.1, г) эпюра углов закручивания φ будет нарастающей от заделки по кривой 2-го порядка, и выпуклость обращена вверх.
Эпюра φ наглядно показывает изменение угла поворота сечения вдоль вала и позволяет выбрать наибольшее значение φmax, которое необходимо для составления второго условия жёсткости (3.6) по φ. Оба условия жёсткости (3.6) позволяют выполнять те же три вида расчётов, что и условие прочности. Поэтому, когда условие жёсткости для рассматриваемого вала не соблюдается, по нему определяют требуемые величины.
Для контроля работоспособности круглых валов нужно иметь в виду, что в поперечном сечении возникают только касательные напряжения (рис. 3.2, а), а на любом наклонном к оси направлении действуют и нормальные, и касательные напряжения. Чтобы показать это, нужно сначала выделить прямоугольный элемент на поверхности вала, по граням которого действуют касательные напряжения = max (рис. 3.3, а). Как известно, это чистый сдвиг. Если рассечь элемент наклонной плоскостью и составить условия равновесия полученного треугольного элемента (рис. 3.3, б), то получаем нормальные и касательные напряжения, действующие на этой площадке:
σα τ sin 2α; τα τ cos 2α.
Площадка под углом α = 45º является особенной: напряжения на ней τα = 0 и σα = . На этой площадке будут только нормальные напря-
89
жения: при = +45º – растягивающие σ1 =σα = + , а при = –45º – сжимающие: σ2 = σα = – . Так, имеем одновременное растяжение и сжатие по
двум взаимно перпендикулярным направлениям (рис. 3.3, в). Эти площадки являются главными, т. к. на них отсутствуют касательные напряжения. Характер разрушения вала зависит от способности данного материала сопротивляться действию и нормальных и касательных напряжений.
Рис. 3.3
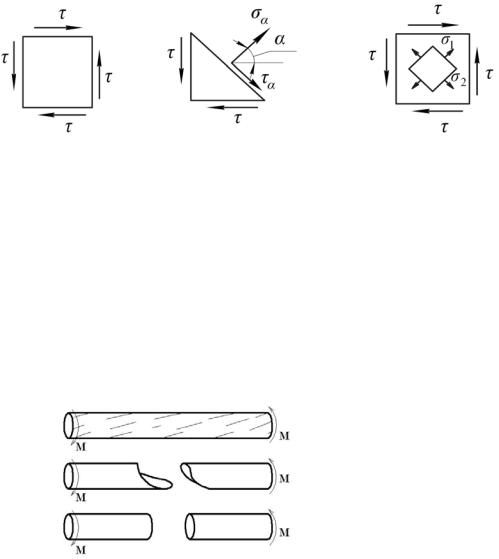
Приведём вид разрушения валов, выполненных из трёх, наиболее распространённых материалов: дерева, стали и чугуна (рис. 3.4).
Деревянный вал претерпевает скалывание продольных волокон относительно друг друга: появляются трещины вдоль образующей. Это происходит вследствие того, что древесина хуже сопротивляется сдвигу (воздействию касательных напряжений τ), чем растяжению и сжатию (воздействию нормальных напряжений σ).
|
а |
Разрушение при кручении: |
|
а – деревянного вала; |
|
|
б – чугунного вала; |
|
|
б |
в – стального вала |
|
в |
Рис. 3.4
Чугунный вал разрушается по винтовым плоскостям, ориентированным под углом 45º к оси бруса. Объяснить такое разрушение можно
тем, что чугун хорошо сопротивляется сжимающим напряжениям σ2 = – , плохо сдвигающим касательным , и хуже всего – растягивающим σ1 = + .
90
В результате по плоскости, перпендикулярной растягивающим нормальным напряжениям σ1 = + (под углом ~α = 45º к оси вала), образуется раз-
рыв по наклонному направлению к оси вала – появляется трещина под углом ~ 45º к оси вала.
Стальной вал срезается по поперечному сечению, где действуют наибольшие касательные напряжения , т. к. сталь хуже всего сопротивляется касательным напряжениям.
Чтобы закрепить знание о напряжённом состоянии при кручении, в РГЗ и КР при расчёте вала можно предусмотреть указывать главные напряжения и описывать место и характер возможного разрушения для разных материалов.
Задача 12 Проектный расчёт ступенчатого вала
Для стального вала заданной конфигурации известны внешние скручивающие моменты (рис. 3.5, а): сосредоточенный момент M 0,6 ml , ин-
тенсивность распределённого скручивающего момента m 1,2 кН·м/м = 1,2 кН, длина l 0,2 м.
Требуется
1.Построить эпюру крутящих моментов M кр .
2.Составить выражения для касательных напряжений max по всем
участкам вала, используя указанные на схеме значения диаметров сечения через неизвестную величину d .
3. Установить наибольший модуль напряжений max и составить ус-
ловие прочности вала по допускаемым напряжениям. Найти из этого условия требуемое значение d при допускаемом напряжении 100 МПа и
назначить диаметры всех участков вала, соблюдая указанное соотношение между ними.
4. Вычислить значения касательных напряжений max по участкам
вала и построить эпюру распределения касательных напряжений по длине вала (эпюру ).
91
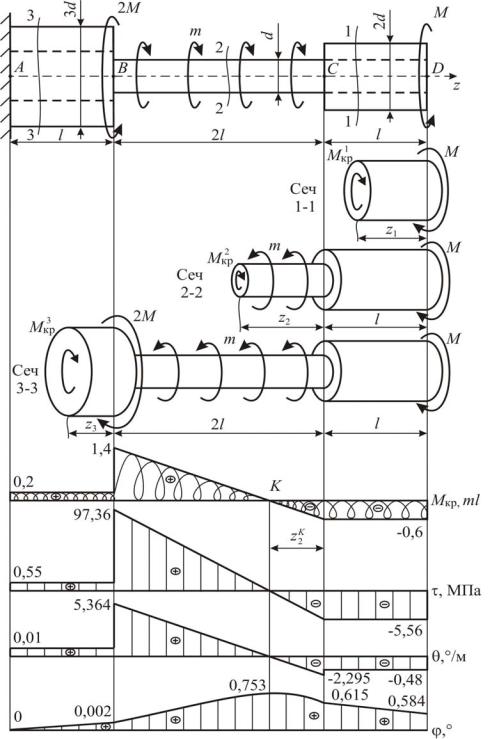
а
б
в
г
д
е
ж
Рис. 3.5
92

5.Вычислить относительные углы закручивания по участкам вала
иабсолютные углы поворота характерных сечений, считая модуль упру-
гости G 0,8 105 МПа. Построить эпюры относительных углов закручивания и абсолютных углов поворота . Проверить жёсткость вала при допускаемых 2 /м и 0,5 . Если условие жёсткости не удовлетво-
ряется, то назначить новые диаметры.
Сечение на участке с большим диаметром принять в виде кольца, для которого соотношение внутреннего и наружного диаметров считать рав-
ным 0,5.
Решение
1. Построение эпюры крутящих моментов
Значения крутящих моментов M кр вычислим методом сечений, рас-
сматривая отсечённые участки со свободного края. При этом крутящий момент в сечении всегда изображаем положительным, т. е. направленным по часовой стрелке (при взгляде на это сечение).
Вал состоит из 3 участков. Уравнение равновесия при кручении (3.1) представляет собой равенство нулю суммы моментов относительно оси вала, т. е. мом z 0 .
Записывая уравнение (3.1) последовательно для всех участков (рис. 3.5, б), получим крутящие моменты:
|
M кр1 |
M 0,6 ml ; |
|||||||
|
M 2 |
M mz |
0,6 ml |
mz |
z2 |
0 |
0,6 ml; |
||
|
кр |
2 |
2 |
z2 |
2l |
0,6 ml m 2l 1,4 ml; |
|||
|
M кр3 |
M m 2l 2M 3M m 2l 3 0,6 ml 2 ml 0,2 ml . |
По этим значениям построим эпюру M кр (рис. 3.5, в).
На участке 2 эпюра крутящих моментов пересекает нулевую линию в точке K . Определим координату точки пересечения z2K :
M кр2 0,6 ml mz2K 0 .
Тогда
z2K 0,6mml 0,6 l .
93

2. Вычисление касательных напряжений
Касательные напряжения max вычислим по формуле
|
max |
M кр |
, |
(3.9) |
|
|
W |
||||
|
где M кр – крутящий момент в рассматриваемом сечении; W |
– полярный |
момент сопротивления этого сечения.
Для сплошного круглого сечения W 16d 3 , для кольцевого сечения
W 16d 3 1 c4 , где c 0,5 – соотношение внутреннего и внешнего диа-
метров.
Составим выражения максимальных касательных напряжений max
для всех участков вала по (3.9). Используем указанные на схеме значения диаметров сечения через неизвестную величину d .
Для 1-го участка сечение кольцевое с внешним диаметром 2d , по-
|
этому |
Mкр1 |
0,6 ml 16 |
0,6 ml 16 |
1,28 ml |
|||||||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||||||
|
max1 |
W |
1 |
1 |
3 |
4 |
d 3 |
|||||||||||||||||||||||||||||||
|
d 3 |
1 c4 |
2d |
1 |
0,5 |
|||||||||||||||||||||||||||||||||
|
Участок 2, |
на котором сечение круглое диаметром d , имеет напря- |
||||||||||||||||||||||||||||||||||||
|
жение |
0,6 ml 16 |
1,28 ml |
|||||||||||||||||||||||||||||||||||
|
Mкр2 0,6 ml mz2 16 |
z2 0 |
; |
|||||||||||||||||||||||||||||||||||
|
max 2 |
d3 |
d3 |
|||||||||||||||||||||||||||||||||||
|
W |
d3 |
z2 2l |
1,4 ml 16 |
22,4 ml |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
d3 |
d3 . |
||||||||||||||||||||||||||||||||||
|
На участке 3 сечение кольцевое с внешним диаметром 3d , поэтому |
|||||||||||||||||||||||||||||||||||||
|
Mкр3 |
0,2 ml 16 |
0,2 ml |
16 |
0,1264 ml |
. |
||||||||||||||||||||||||||||||||
|
max 3 |
W |
3 |
3 |
3 |
4 |
d3 |
|||||||||||||||||||||||||||||||
|
d 3 |
1 c4 |
3d |
1 |
0,5 |
|||||||||||||||||||||||||||||||||
3. Составление условия прочности и подбор диаметров
Условие прочности вала при кручении по допускаемым напряжениям по (3.4) имеет вид
|
τmaxmax |
Mкр |
τ , |
|||
|
W |
|||||
|
ρ |
max |
94
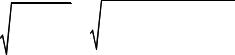
где τmaxmax – наибольшее по модулю значение касательных напряжений max ,
которое выбираем из полученных значений. Получаем
max 22,4 ml .
max d 3
Подставим maxmax в условие прочности: 22,4 ml ,
d 3
где – допускаемое касательное напряжение. Отсюда найдём требуемое значение d :
|
d 3 |
22,4 ml |
3 |
22,4 1,2 103 |
0,2 |
0,0258 м 2,58 см. |
|
|
100 106 |
||||||
Округляя в большую сторону, принимаем d 2,6 см. Далее назнача-
ем диаметры всех участков вала, соблюдая указанные соотношения между ними:
d1 2d 2 2,6 5,2 см; d2 d 2,6 см; d3 3d 3 2,6 7,8 см.
4. Вычисление значений касательных напряжений
Используя полученные выше выражения τmax , подсчитаем касательные напряжения по участкам вала:
|
τ |
1,28 ml |
1,28 1,2 103 0,2 |
5,56 10 |
6 |
Па |
5,56 МПа; |
|||||||||||||
|
max1 |
π d3 |
π 0,026 3 |
|||||||||||||||||
|
z2 |
0 |
1,28 ml |
1,28 1,2 103 |
0,2 |
5,56 106 Па 5,56 МПа; |
||||||||||||||
|
d |
3 |
0,026 3 |
|||||||||||||||||
|
max 2 |
|||||||||||||||||||
|
22,4 ml |
22,4 1,2 103 0,2 |
||||||||||||||||||
|
z2 |
2l |
97,36 |
10 |
6 |
Па 97,36 МПа; |
||||||||||||||
|
d |
3 |
0,026 3 |
|||||||||||||||||
|
0,1264 ml |
0,1264 1,2 103 0,2 0,55 106 |
Па 0,55 МПа. |
|||||||||||||||||
|
max 3 |
d3 |
0,026 3 |
Откладывая полученные значения от базисной линии, построим эпюру распределения касательных напряжений по длине вала − эпюру
(рис. 3.5, г).
95

5. Вычисление углов закручивания и проверка жёсткости
Относительные и абсолютные углы закручивания по участкам вала вычислим по следующим формулам:
|
M кр |
l |
M кр |
d z , |
|||
|
; |
(3.10) |
|||||
|
GI |
GI |
|||||
|
0 |
где G – модуль упругости второго рода или модуль при сдвиге; I – полярный момент инерции сечения; l – длина участка вала.
Для сплошного круглого сечения I 32d 4 , для кольцевого сечения
I 32d 4 1 c4 , где c 0,5 – соотношение внутреннего и внешнего диа-
метров.
На 1-м участке, где сечение кольцевое диаметром 5,2 см, по (3.10) находим
|
M кр1 |
0,6 ml |
32 |
0,6 1,2 103 0,2 32 |
||||||||||||||||
|
1 |
G1I 1 |
G d14 1 c4 |
0,8 1011 0,052 4 |
1 0,54 |
|||||||||||||||
|
0,002675 рад 0,002675 |
180 |
0,153 |
/ м; |
||||||||||||||||
|
l |
Mкр1 |
Mкр1 l |
|||||||||||||||||
|
1 |
d z1 |
0,153 |
0,2 0,031 . |
||||||||||||||||
|
G I |
1 |
GI |
1 |
||||||||||||||||
|
0 |
1 |
На 2-м участке сечение круглое диаметром 2,6 см, по (3.10) получим
|
M кр 2 |
0,6 ml mz2 32 |
z2 |
0 |
0,6 ml 32 |
||||||||||||||||||
|
2 |
G d24 |
|||||||||||||||||||||
|
G d24 |
1,4 ml 32 |
|||||||||||||||||||||
|
G2 I 2 |
z2 |
2l |
||||||||||||||||||||
|
G d24 |
||||||||||||||||||||||
|
z |
0 |
0,6 |
1,2 |
103 |
0,2 32 |
0,040122 |
180 |
2,299 / м; |
||||||||||||||
|
2 |
0,8 1011 |
0,026 4 |
||||||||||||||||||||
|
z |
2l |
1,4 |
1,2 103 |
0,2 32 |
0,093617 |
180 |
5,364 |
/ м; |
||||||||||||||
|
2 |
0,8 |
1011 |
0,026 4 |
|||||||||||||||||||
|
2l |
M кр 2 |
2l |
0,6 ml mz2 |
32 |
||||||||||||||||||
|
2 |
d z2 |
4 |
d z2 |
|||||||||||||||||||
|
G2 I 2 |
||||||||||||||||||||||
|
0 |
0 |
G d2 |
96
|
0,6 ml z2 |
0,5 mz22 32 |
2l |
0,6 ml 2l2 0,5 m 2l 2 32 |
||||||||||||||||||||||
|
G d24 |
0 |
G d24 |
|||||||||||||||||||||||
|
0,8 ml 2 32 |
0,8 1,2 103 |
0,22 |
32 |
180 |
|||||||||||||||||||||
|
G d24 |
0,8 1011 |
0,026 4 0,010699 |
0,613 /м. |
||||||||||||||||||||||
|
На 3-м участке имеем сечение кольцевое диаметром 7,8 см, по (3.10) |
|||||||||||||||||||||||||
|
получим |
|||||||||||||||||||||||||
|
M кр3 |
0,2 ml 32 |
0,2 1,2 103 |
0,2 |
32 |
|||||||||||||||||||||
|
3 |
G3 I 3 |
G d34 1 c4 |
0,8 1011 0,078 4 1 0,54 |
||||||||||||||||||||||
|
0,000176 |
180 |
0,010 / м; |
|||||||||||||||||||||||
|
l |
M кр3 |
d z3 |
M кр3 |
l |
|||||||||||||||||||||
|
3 |
0,010 0,2 0,002 . |
||||||||||||||||||||||||
|
G I |
3 |
GI |
3 |
||||||||||||||||||||||
|
0 |
3 |
Определим углы поворота характерных сечений, обозначив сечения буквами A , B , C , D . Так как точкаA находится в заделке, A 0 ; далее
используя формулу (3.7), найдём углы поворота следующих сечений:
B 3 0,002 ; C 3 2 0,002 0,613 0,615 ;
D 3 2 1 0,002 0,613 0,031 0,584 .
Согласно линейному закону изменения крутящих моментов на 2-м
|
участке имеем пересечение нулевой линии при zK |
0,6ml 0,6l . В этом |
||||||||||||||||||||
|
2 |
m |
||||||||||||||||||||
|
сечении наблюдается экстремальный угол закручивания φ K , |
значения ко- |
||||||||||||||||||||
|
торого нужно найти. Сначала вычислим угол закручивания участка CK: |
|||||||||||||||||||||
|
0,6 l |
M кр 2 |
d z2 |
0,6 ml z2 |
0,5 mz22 32 |
0,6 l |
||||||||||||||||
|
CK |
0 |
||||||||||||||||||||
|
G |
d24 |
0 |
|||||||||||||||||||
|
G2 I 2 |
|||||||||||||||||||||
|
0,6 ml 0,6 l 0,5 m 0,6 l 2 32 |
0,18 ml 2 |
32 |
|||||||||||||||||||
|
G d24 |
G d24 |
||||||||||||||||||||
|
0,18 1,2 103 0,22 |
32 |
0,002407 |
180 |
0,138 / м. |
|||||||||||||||||
|
0,8 1011 0,026 |
4 |
||||||||||||||||||||
Далее найдём угол поворота сечения K, используя формулу (3.7):
97
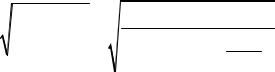
K C CK 0,615 0,138 0,753 .
По полученным значениям построим эпюры относительных углов закручивания и абсолютных углов поворота сечений (рис. 3.5, д, е).
Выберем из полученных значений и наибольшие по модулю:
max 5,364 / м; max 0,753 .
Теперь проверим вал по условиям жёсткости (3.5), по которым должно быть следующее:
max и max .
В нашем случае имеем
5,364 / м 2 / м и 0,753 0,5 .
Как видно, условие жёсткости не выполняется. Необходимо назначить новые диаметры из условия жёсткости (3.5). Удобно вычислять через относительные углы закручивания, поэтому условие жёсткости в нашем случае выглядит так:
|
Отсюда |
||
|
d 4 |
1,4 ml 32 |
4 |
|
G π θ |
Принимаем d 3,4
вала:
d1 2d 2 3,4 6,8
max 1,4 ml 32 .
G d 4
1,4 1,2 103 0,2π 32 0,03327 м 3,327см. 0,8 1011 π2180°
см и окончательно назначаем диаметры участков
см; d2 d 3,4 см; d3 3d 3 3,4 10,2 см.
Задача 13 Проектный расчёт ступенчатого статически неопределимого вала
Стальной ступенчатый вал заданной конфигурации имеет жёсткие защемления с торцов (рис. 3.6, а). Известны внешние скручивающие моменты, для которых M 1,25 ml; m 1,2 кН·м/м = 1,2 кН; длина l 0,2 м.
98
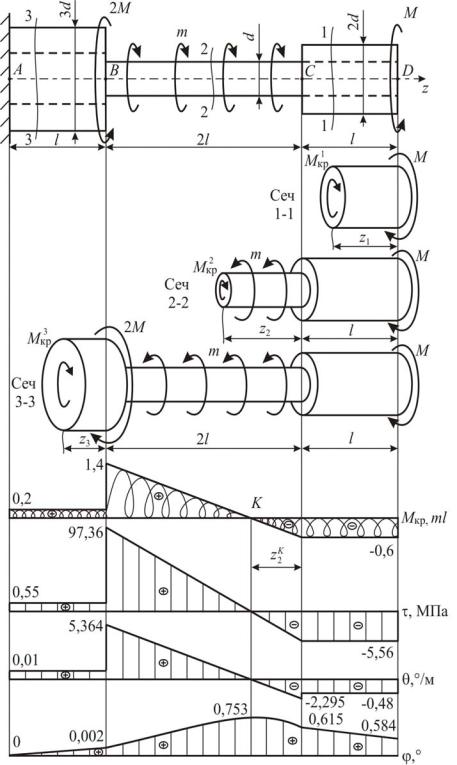
а
б
в
г
д
е
Рис. 3.6
99
Требуется
1.Используя уравнение равновесия и уравнение перемещений, найти величины реактивных моментов, возникающих в жёстких заделках.
2.Построить эпюру крутящих моментов M кр.
3.Составить выражения для касательных напряжений max по всем
участкам вала, используя указанные на схеме значения диаметров сечения через неизвестную величину d .
4. Установить наибольший модуль напряжений max и составить усло-
вие прочности вала по допускаемым напряжениям. Найти из этого условия требуемое значение d при допускаемом напряжении τ 80 МПа и назначить
диаметры всех участковвала, соблюдаяуказанноесоотношениемежду ними. 5. Вычислить значения касательных напряжений max по участкам
вала и построить эпюру распределения касательных напряжений по длине вала (эпюру ).
6.Вычислить относительные углы закручивания по участкам вала
иабсолютные углы поворота характерных сечений, считая модуль упру-
гости G 0,8 105 МПа. Построить их эпюры. Проверить жёсткость вала при допускаемых 2 /м и 0,5 . Если условие жёсткости не удов-
летворяется, то назначить новые диаметры.
Сечение на участке с большим диаметром принять в виде кольца, для которогосоотношениевнутреннегоинаружногодиаметровсчитатьравным0,5.
Решение
1. Нахождение реактивных моментов
Обозначим реактивные моменты, возникающие в жёстких заделках, M A и MC (рис. 3.6, а). Их величины должны удовлетворять уравнению
равновесия всего вала, которое при кручении записываем по (3.1):
|
M A M MC 0 . |
(3.11) |
|
Как видно, это уравнение содержит два неизвестных M A |
и MC , по- |
этому вал является статически неопределимым. Для нахождения M A и MC необходимо составить еще одно уравнение – уравнение перемещений.
При кручении уравнение перемещений записывают через углы закручивания участков . Данный вал состоит из двух участков, поэтому
где для 1 и 2 используем выражения (3.10).
100

Итак, величины реактивных моментов найдём, используя уравнение равновесия (3.11) и уравнение перемещений (3.12).
Необходимые выражения крутящих моментов для всех участков вала (рис. 3.6, б) получим из уравнений равновесия отсечённых частей:
M кр1 M A ; Mкр2 M A M.
Далее запишем по (3.10) углы закручивания:
|
1 |
Mкр1 l1 |
M |
A |
2l |
; 2 |
Mкр2 |
l2 |
M |
A |
M l |
. |
||||
|
GI 1 |
GI 2 |
GI 2 |
|||||||||||||
|
GI 1 |
Здесь полярные моменты инерции сечения участков принимают следующие значения:
|
I 1 |
d 4 |
1 c |
4 |
d 4 |
1 c |
4 |
; I 2 |
d |
4 |
0,7d 4 |
. |
|||
|
32 |
32 |
32 |
32 |
|||||||||||
|
1 |
2 |
Подставляя найденные величины в (13.2), получим уравнение перемещений:
|
M A 2 l 32 |
M A M l 32 |
0. |
|||
|
G d 4 1 c4 |
G 0,7d 4 |
||||
|
После сокращения имеем |
M A M |
||||
|
M A 2 |
|||||
|
1 c4 |
0,7 4 |
0 |
или
6,298 M A 4,165 M 0.
Вычислим из этого уравнения реактивный момент
MA 4,1656,298M 0,661M 0,6611,25ml 0,826ml 0,826 1,2 103 0,2 198,4 Н м.
Второй реактивный момент можно не вычислять, его значение получится при построении эпюры крутящих моментов.
2. Построение эпюры крутящих моментов
Подставив найденный момент M A в выражения крутящих моментов по участкам, получим:
Mкр1 M A 0,826 ml 198,4 Н м;
101

Mкр2 MA M 0,826ml 1,25ml 0,424ml 0,424 1,2 103 0,2
101,6 Н м.
Откладывая эти значения от базисной линии на рис. 3.6, в, построим эпюру крутящих моментовMкр.
3. Нахождение выражений для касательных напряжений.
Вычислим касательные напряжения по (3.9), для которых полярные моменты сопротивления W участков вала запишем согласно заданным
значениям диаметров сечения через величину d :
|
W |
d13 |
1 c4 |
d 3 |
1 c4 ; W |
d23 |
0,7d 3 |
. |
|
|
1 |
16 |
16 |
2 |
16 |
16 |
|||
Максимальные касательные напряжения τmax по участкам получают следующие выражения:
|
max 1 |
M |
кр1 |
0,826 ml 16 |
14,097 ml |
; |
||||||||||||||||
|
W 1 |
d 3 1 |
0,54 |
d 3 |
||||||||||||||||||
|
max 2 |
M кр 2 |
M |
A |
M 16 |
0,424 ml 16 |
19,778 ml |
. |
||||||||||||||
|
d33 |
0,7d 3 |
d 3 |
|||||||||||||||||||
|
W 2 |
|||||||||||||||||||||
4. Составлениеусловияпрочностииопределениеразмеровсечения
Из полученных значений касательных напряжений выбираем наибольшее по модулю и составим условие прочности по (3.4):
19,778 ml .
d 3
Найдём из этого условия требуемое значение d:
|
d 3 |
19,778 ml |
3 |
19,778 1,2 103 0,2 |
0,0266 м 2,66 см. |
|
|
80 106 |
|||||
Принимаем d 2,7 см. Назначаем диаметры всех участков вала, соблюдая указанные соотношения между ними:
d1 d 2,7 см; d2 0,7d 0,7 2,7 1,9см; d3 3d 3 3,4 10,2 см.
102
5. Вычисление значений касательных напряжений
Вычислим значения касательных напряжений max по участкам вала, используя полученные выражения:
|
14,097 ml |
14,097 1,2 103 |
0,2 |
54,71 10 |
6 |
Па 54,71 МПа; |
|||||
|
max 1 |
d3 |
0,027 3 |
||||||||
|
max 3 |
19,778 ml |
19,778 1,2 103 0,2 |
76,76 10 |
6 |
Па 76,76 МПа. |
|||||
|
d 3 |
0,027 3 |
|||||||||
Откладывая полученные значения в масштабе на рис. 3.6, г, построим эпюру распределения касательных напряжений по длине вала (эпюру ).
6. Вычисление углов закручивания
Вычислим относительные углы закручивания и углы закручивания участков вала по записанным выражениям.
Участок 1 имеет сечение кольцевое диаметром 2,7 см, поэтому
|
M кр1 |
0,826 ml 32 |
0,826 1,2 103 |
0,2 32 |
||||||||||||||||||||||||||||||||||
|
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||||||||||||||||
|
G I |
G |
d |
4 |
c |
4 |
11 |
4 |
1 |
0,5 |
4 |
|||||||||||||||||||||||||||
|
0,8 10 |
0,027 |
||||||||||||||||||||||||||||||||||||
|
0,050661 |
180 |
2,90 / м; |
|||||||||||||||||||||||||||||||||||
|
1 |
M кр1 2l |
2l 2,90 2 0,2 1,16 . |
|||||||||||||||||||||||||||||||||||
|
G1I 1 |
1 |
||||||||||||||||||||||||||||||||||||
|
Для 2-го участка, где сечение круглое диаметром 1,9 см, |
|||||||||||||||||||||||||||||||||||||
|
θ |
Mкр2 |
0,424 ml 32 |
0,424 1,2 103 |
0,2 32 |
|||||||||||||||||||||||||||||||||
|
2 |
G2 Iρ2 |
G |
π |
0,7d 4 |
0,8 1011 π 0,019 4 |
||||||||||||||||||||||||||||||||
|
0,101541 |
180 |
5,82 / м; |
|||||||||||||||||||||||||||||||||||
|
2 |
Mкр2 |
l |
2 |
l 5,82 0,2 1,16 . |
|||||||||||||||||||||||||||||||||
|
G2 I 2 |
Определим углы поворота характерных сечений по (3.7), обозначив сечения буквами A, B , C . Так как точкаA находится в заделке, то
A 0 ; B 1 1,16 ; C 1 2 1,16 1,16 0 .
103

Угол поворота в сечении C оказался равным нулю, поскольку это сечение находится в заделке. По полученным значениям построим эпюры относительных углов закручивания и абсолютных углов поворота ха-
рактерных сечений (рис. 3.6, д, е).
7. Проверка вала по условиям жёсткости
Выберем из полученных значений наибольшие по модулю:
max 5,364 / м и max 1,16 .
Проверим вал по условию жёсткости (3.5), в нашем случае имеем:
|
5,82 / м 2 / м; |
1,16 0,5 . |
Условие жёсткости не выполняется. Необходимо назначить новые диаметры из условия жёсткости, которые запишем через относительные углы закручивания:
|
0,424 ml 32 |
. |
|||
|
max |
G 0,7d 4 |
Отсюда
|
d 4 |
0,424 ml 32 |
0,424 1,2 103 |
0,2 32 |
0,0353 м 3,53 см. |
|||||
|
G 0,7 |
4 |
4 0,8 1011 0,7 4 |
2 |
||||||
|
180 |
|||||||||
Принимаем величину d 3,6 см и окончательные диаметры участков
вала:
d1 d 3,6 см; d2 0,7d 0,7 3,6 2,52 см.
Задача 14 Проверочный расчёт ступенчатого вала
Для круглого стального ступенчатого вала (рис. 3.7) известны внешние сосредоточенные и распределённые моменты, заданы размеры поперечного сечения и длины участков. На более широком участке вала считать сечение кольцевым с соотношением внутреннего диаметра к наруж-
ному с = 0,3.
104
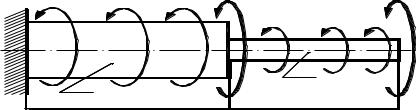
Требуется
1. Построить эпюры крутящих моментов Мкр, касательных напряжений τ относительных углов закручивания θ и абсолютных углов поворота сечений вала φ. Модуль упругости принять G = 0,8· 5 МПа.
2.Указать опасное сечение и значение τmax, проверить прочность при допускаемом напряжении τ = 100 МПа. Если условие прочности не удовлетворяется, то указать диаметры, при которых оно будет соблюдаться.
3.Указать значения θmax и φmax, проверить жёсткость при допускае-
мом относительном угле закручивания θ = 2,5 º/м и допускаемом абсолютном угле поворота сечения φ = 1º. Если условие жёсткости не удовлетворяется, то указать диаметры, при которых оно будет соблюдаться.
Решение
В этой задаче использована унифицированная схема ступенчатого вала (рис. 3.7), в которой на валу в начале каждого участка приложены сосредоточенные моменты Мi, на каждом участке действует распределённый крутящий момент интенсивности mi.. Принимаем следующее правило знаков для внешних моментов: за положительное считаем направление внешних моментов против часовой стрелки (при взгляде на сечение).
|
m |
M |
2 |
M |
1 |
||
|
2 |
||||||
|
m |
1 |
|||||
|
d |
1 |
|||||
|
d |
2 |
|||||
|
L |
2 |
L |
1 |
Рис. 3.7
Пусть заданы следующие величины: сосредоточенные моменты в начале участков равны М1 = 0,12 кН·м и М2 = 0; интенсивность распределённого моментапоучасткамm1 = 0 иm2 = –2 кН·м/м= –2 кН; длиныучастковl1 = 0,26 м и l 2 = 0,18 м; диаметры сечений участков d1 = 25 мм и d2 = 30 мм.
Сначала по этим исходным данным изобразим в масштабе схему заданного вала и действующую на него нагрузку (рис. 3.8, б). Вал имеет два грузовых участка, здесь нумерацию участков удобно брать со свободного края, поэтому начало 1-го участка положим на торце вала.
105

1. Построение эпюр крутящих моментов, напряжений и угловых деформаций
Для оценки прочности и жёсткости вала необходимо иметь значения крутящих моментов M кр , касательных напряжений max , относительных
углов закручивания θ и углов закручивания φ участков вала.
Вычисление значений крутящих моментов выполняем методом сечений по уравнению суммы моментов относительно оси вала (3.1)
мом z 0 . При этом положительный внутренний крутящий момент в се-
чении направляем по часовой стрелке (напомним: такое правило существует для внутреннего момента). Для вычисления max , и φ используем
следующие формулы:
|
Mкр |
Mкр |
l Mкр |
||||||
|
τmax |
; θ |
; Δφ |
d z, |
|||||
|
W |
GI |
ρ |
GI |
ρ |
||||
|
где Wρ – полярный |
ρ |
0 |
||||||
|
момент |
сопротивления круглого сечения, |
Wρ π32d3 1 c4 , где c 0,3 – соотношение внутреннего и внешнего диаметров; G – модуль упругости второго рода или модуль сдвига; Iρ – поляр-
ный момент инерции круглого сечения, Iρ π32d4 1 c4 ; l – длина участка вала.
1-й участок 0 z1 l 1 = 0,26 м. В текущем сечении (рис. 3.8, а), удалённом от начала 1-го участка на расстоянии z1, крутящий момент Mкр1 ,
|
касательные напряжения |
τmax 1 |
, относительный угол закручивания θ1 и |
||||||||||||||||||||||
|
угол закручивания участка φ1 |
принимают значения: |
|||||||||||||||||||||||
|
Mкр1 M 0,12 |
кН м; |
|||||||||||||||||||||||
|
τ |
Mкр1 |
0,12 103 |
16 |
39,1 МПа; |
||||||||||||||||||||
|
W |
0,0253 |
|||||||||||||||||||||||
|
max1 |
||||||||||||||||||||||||
|
ρ1 |
||||||||||||||||||||||||
|
θ |
Mкр1 |
0,12 32 103 |
180° |
2,24 º/м; |
||||||||||||||||||||
|
1 |
GIρ1 |
0,8 1011 π 0,025 4 |
π |
|||||||||||||||||||||
|
l |
M |
M |
||||||||||||||||||||||
|
φ |
0 |
кр1 |
d z |
кр1 |
l l |
2,24 0,26 0,582º. |
||||||||||||||||||
|
1 |
||||||||||||||||||||||||
|
G Iρ1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||
|
G Iρ1 |
2-й участок 0 z2 l2 = 0,18 м. В текущем сечении 2-го участка (рис. 3.8, б), удалённом от его начала на расстоянии z2, крутящий момент
Mкр2 , касательные напряжения τmax 2 , относительный угол закручивания θ2 и угол закручивания участка φ2 принимают значения:
106
|
Mкр2 M m2 z2 |
0,12 – 2 z2 |
z2 0 |
0,12 |
кН м, |
|||||||||||||||||||||||||||||||||||
|
z2 0,18 м |
0,24кН м; |
||||||||||||||||||||||||||||||||||||||
|
τ |
max 2 |
Mкр2 |
0,12 – 2 z2 16 |
z2 0 |
τmax2 |
22,8, |
|||||||||||||||||||||||||||||||||
|
Wρ2 |
π 0,033 (1 0,34 ) |
z2 0,18м |
τmax2 |
45,7; |
|||||||||||||||||||||||||||||||||||
|
M |
кр2 |
0,12 – 2 z2 32 103 |
180 |
z2 |
0 1,09 °/м, |
||||||||||||||||||||||||||||||||||
|
θ 2 |
z2 0,18м |
||||||||||||||||||||||||||||||||||||||
|
2 |
11 |
π 0,03 |
4 |
4 |
) |
π |
2,18 °/м; |
||||||||||||||||||||||||||||||||
|
G I |
0,8 10 |
(1 0,3 |
|||||||||||||||||||||||||||||||||||||
|
l2 |
Mкр2 |
l2 |
0,18 |
0,12 – 2z2 32 103 |
180 |
||||||||||||||||||||||||||||||||||
|
φ2 |
0 |
d z2 |
0 |
d z2 |
|||||||||||||||||||||||||||||||||||
|
G I 2 |
0,8 1011 π 0,034 (1 0,34 ) |
π |
|||||||||||||||||||||||||||||||||||||
|
0,12z2 |
– 2z2 |
2 / 2 |
00,18 |
32 103 |
180° |
||||||||||||||||||||||||||||||||||
|
11 |
4 |
4 |
π |
||||||||||||||||||||||||||||||||||||
|
0,8 10 π |
0,03 (1 |
0,3 ) |
|||||||||||||||||||||||||||||||||||||
|
( 0,0108) 32 103 |
180° |
0,098°. |
|||||||||||||||||||||||||||||||||||||
|
11 |
π |
4 |
4 |
π |
|||||||||||||||||||||||||||||||||||
|
0,8 10 |
0,03 |
(1 0,3 ) |
Как и следовало ожидать, на участке с распределённым моментом крутящий момент, напряжение и относительный угол закручивания изменяются по линейному закону.
Определим углы поворота характерных сечений, обозначив сечения буквами A, B , C . Так как точкаA находится в заделке, то
φA 0 ; φ B φ 2 0,098 ;
φC φ 2 φ1 0,098 0,582 0,484 .
Видим, что на 2-м участке значения крутящих моментов проходят через 0, и эпюра Mкр 2 в таком случае пересечёт нулевую линию. Обозна-
чим это сечение точкой К, а координату этого сечения как z0 . Необходимо
помнить, что это характерное сечение имеет важную особенность: для него угол закручивания вала К принимаем экстремальное значение для этого
участка, а на криволинейной эпюре φ будет перегиб.
Определим координату z0 , используя равенство крутящего момента Mкр 2 в сечении К нулю. Составим уравнение:
Mкр2 0,12 2z0 0 ,
из которого получаем z0 0,06 м. Теперь вычислим угол закручивания
участка CK, подставляя в угол закручивания 2-го участка границы интегрирования от 0 до z0 0,06 м:
107
z0
φCK
0
0,12z2
а
б
в
г
д
е
|
Mкр2 |
z0 |
0,06 |
0,12 – 2z2 32 103 |
180 |
||||||||
|
d z2 |
0 |
d z2 |
||||||||||
|
G Iρ2 |
0,8 1011 π 0,034 (1 0,34 ) |
π |
||||||||||
|
– 2z2 |
2 / 2 |
0,06 |
32 103 |
180° |
0,033°. |
|||||||
|
11 |
4 |
4 |
||||||||||
|
0 |
0,8 10 |
π 0,03 |
(1 0,3 ) |
π |
||||||||
Далее согласно (3.7) и зная φCK , найдём угол поворота сечения K:
φ K φ B φCK 0,098 0,033 0,131 .
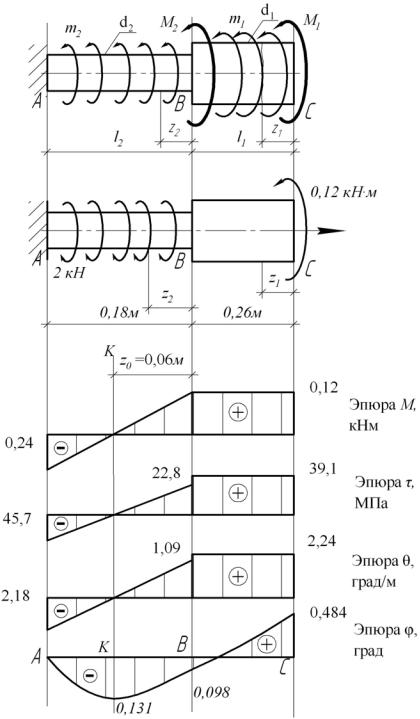
По полученным значениям построим эпюры изменения по длине вала крутящих моментов Mêð , касательных напряжений τmax, относительных углов
закручиванияθиабсолютныхугловповоротаφсечений(рис. 3.8, в, г, д, е).
2–3. Проверка прочности и жёсткости вала
Укажем наибольшие по абсолютной величине значения напряжений и углов закручивания:
τmax = 45,7 МПа; θmax =2,18 º/м; φмах = 0,484º.
Сделаем выводы о прочности и жёсткости вала:
τmax = 45,7 МПа < [τ] = 100 MПa;
θmax = 2,18 /м < [θ] =2,5 /м; φmах = 0,484º < [φ] = 1 ,
значит, прочность и жёсткость вала обеспечены.
Задача 15 Проверочный расчёт ступенчатого статически неопределимого вала
Стальной ступенчатый вал (схема изображена на рис. 3.9) имеет жёсткие заделки по торцам. Известны внешний сосредоточенный и распределённые моменты, заданы диаметры поперечного сечения и длины участков.
На более широком участке вала считать сечение кольцевым с соотношением внутреннего диаметра к наружному с = 0,3.
|
m 2 |
M |
|
m 1 |
|
|
d 1 |
|
|
d 2 |
|
|
L 2 |
L 1 |
|
Рис. 3.9 |
109
Требуется
1.Используя условие равновесия и уравнение перемещений, найти величины реактивных моментов, возникающих в жёстких заделках.
2.Построить эпюры крутящих моментов Мкр, касательных напряжений τ, относительных углов закручивания θ и абсолютных углов поворота
φ. Модуль упругости G = 0,8· 5 МПа.
3.Указать опасное сечение и значение τmax, проверить прочность при допускаемом напряжении τ = 100 МПа. Если условие прочности не выполняется, указать диаметры, при которых оно будет удовлетворено.
4.Указать значения θmax и φmax, проверить жёсткость при допускае-
мом относительном угле закручивания θ = 2 /м и допускаемом абсолют-
ном угле поворота сечения φ = 0,5 . Если условие жёсткости не выполняется, указать диаметры, при которых оно выполняется.
Решение
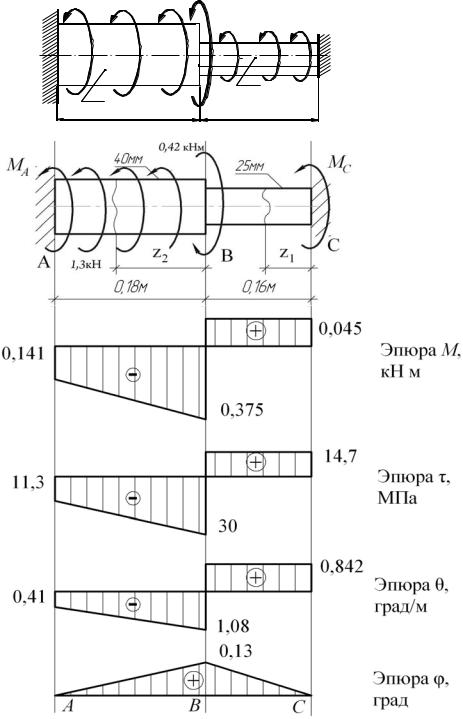
В этой задаче использована унифицированная схема ступенчатого вала (рис. 3.9): в начале участка приложен сосредоточенные момент М, и на каждом участке действует распределённый крутящий момент интенсивности m. Пусть заданы следующие величины: сосредоточенный момент М = –0,42 кН·м; интенсивность распределённого момента m1 = 0 и m2 = 1,3 кН·м/м = 1,3 кН; длины участков l1 = 0,16 м и l 2 = 0,18 м; диаметры сечений участков d1 = 25 мм и d2 = 40 мм.
Сначала изобразим по этим данным в масштабе заданный вал и действующую на него нагрузку (рис. 3.10, б). Вал разделим на два грузовых участка; нумерацию участков возьмём справа, начало 1-го участка положим на торце вала в сечении С.
1. Определение реактивных моментов
Обозначим реактивные моменты, возникающие в жёстких заделках, как MА и MС. Вал является статически неопределимым. Составим два уравнения.
Первое – уравнение равновесия вала по (3.1):
мом z 0 : M A 0,42 1,3 0,18 MC 0.
Второе – уравнение перемещений. Для вала с двумя заделками угол поворота заделок относительно друг друга равен нулю, можно записать уравнение перемещений в виде
АC CA 0.
110
|
m 2 |
M |
|
|
m 1 |
||
|
а |
||
|
d 1 |
||
|
d 2 |
||
|
L |
2 |
L 1 |
б
в
г
д
е
Рис. 3.10
Расписать это уравнение через нагрузку можно двумя приёмами. Первый из них заключается в записи двух углов закручивания 1 и 2
через крутящий момент по формуле угла закручивания:
111

|
l1 |
M 1 |
l2 M 2 |
|||||||||
|
φ |
кр |
d z ; φ |
кр |
d z |
, |
||||||
|
1 |
0 |
2 |
0 G I 2 |
||||||||
|
G Iρ1 |
1 |
2 |
|||||||||
и дальнейшей записи их суммы, равной нулю:
1 + 2 = 0.
По второму приёму учитываем влияние каждого слагаемого Mкр на
деформацию: сосредоточенный момент закручивает на угол φ Ml , а
GIρ
|
распределённый – на угол φ l |
mz |
d z mz2 / 2 . |
|
0 G Iρ |
G Iρ |
Запишем угол CA как сумму углов от момента MC , момента0,42 кН·м и распределённого момента m =1,3кН. Начинаем с левого торца бруса и получаем следующее уравнение перемещений:
|
MС 0,16 32 |
MC 0,18 0,42 0,18+1,3 0,182 |
/ 2 32 |
0. |
||||
|
G π 0,025 |
4 |
4 |
4 |
||||
|
G π 0,04 1 |
0,3 |
||||||
Такое же уравнение получим и после подстановки углов закручивания участков вала в сумму 1 + 2 = 0. Из последнего уравнения
MC 0,045 кН·м, а из уравнения равновесия M A = 0,141 кН·м.
2. Построение эпюр крутящих моментов, напряжений и деформаций
Для оценки прочности и жёсткости вала запишем значения крутящих моментов Mкр , касательных напряжений τmax, относительных углов закру-
чивания θ и углов закручивания φ участков вала:
τmax Mкр ; θ MGIкр ; Δφ l MGIкр d z,
ρ0 ρ
где Wρ – полярный момент сопротивления сечения, для кольцевого сечения
Wρ π32d3 1 c4 , где c 0,3 – соотношение внутреннего и внешнего диаметров; G – модуль упругости второго рода или модуль сдвига; Iρ – полярный момент инерции круглого сечения, Iρ π32d4 1 c4 ; l – длина участка вала.
112
1-й участок 0 z1 l1 = 0,16 м. Для 1-го участка в текущем сечении (рис. 3.10, б), удалённом от торца С на расстоянии z1, крутящий момент
|
M 1кр , касательные напряжения |
τ1max , относительный угол закручивания |
||||||||||||||||||
|
θ1 и угол закручивания участка φ1 |
принимают значения: |
||||||||||||||||||
|
1 |
1 |
Mкр |
1 |
0,045 103 16 |
|||||||||||||||
|
Mкр MС 0,045кН·м; τmax |
3 |
14,7 МПа; |
|||||||||||||||||
|
W |
1 |
π |
|||||||||||||||||
|
0,025 |
|||||||||||||||||||
|
ρ |
|||||||||||||||||||
|
θ |
M 1кр |
0,045 32 103 |
180 |
0,842 /м; |
|||||||||||||||
|
1 |
G Iρ1 |
0,8 1011 |
π |
0,025 4 |
π |
||||||||||||||
|
l |
M 1 |
M 1 l |
|||||||||||||||||
|
φ1 |
кр |
d z1 |
кр |
1 l1 |
0,842 0,16 0,135 0,14 . |
||||||||||||||
|
GIρ1 |
|||||||||||||||||||
|
0 |
G Iρ1 |
||||||||||||||||||
|
2-й участок 0 z2 |
l 2 = 0,18 м. В текущем сечении участка (рис. |
3.10, б), удалённом от его начала на расстоянии z2, крутящий момент Mкр 2 ,
|
касательные напряжения |
τmax 2 , относительный угол закручивания θ2 и |
||||||||||||||||||||||||||
|
угол закручивания участка φ2 |
получают значения: |
||||||||||||||||||||||||||
|
Mкр2 МС + M m2 z2 0,045 – 0,42 +1,3z2 0,375 +1,3z2 , |
|||||||||||||||||||||||||||
|
при z2 0 |
0,375 кН м; при z2 0,18м |
0,141кН м; |
|||||||||||||||||||||||||
|
τmax 2 |
Mкр2 |
( 0,375 +1,3 z2 ) 16 |
при z2 0 |
τmax 2 30 МПа, |
|||||||||||||||||||||||
|
Wρ2 |
π 0,04 |
3 |
4 |
при z2 0,18м |
τmax 2 11,3 МПа; |
||||||||||||||||||||||
|
(1 0,3 ) |
|||||||||||||||||||||||||||
|
θ 2 |
Mкр2 |
0,375 1,3z2 32 103 |
180 |
( 1,08 3,74z2 ), |
|||||||||||||||||||||||
|
11 |
π |
0,04 |
4 |
4 |
π |
||||||||||||||||||||||
|
G Iρ2 |
0,8 10 |
(1 0,3 ) |
|||||||||||||||||||||||||
|
при z2 |
0 |
θ 2 1,08°/м; |
при z2 0,18м |
θ2 0,41°/м; |
|||||||||||||||||||||||
|
l2 |
Mкр2 |
0,18 |
0,375 +1,3z2 32 103 |
180 |
|||||||||||||||||||||||
|
φ2 |
0 |
d z2 0 |
d z2 0,14 . |
||||||||||||||||||||||||
|
G Iρ2 |
0,8 1011 π 0,044 (1 0,34 ) |
π |
Определим углы поворота характерных сечений A , B и C . Так как точкаA находится в заделке, то
A 0 ; φ B =Δφ 2 0,14 ; φВ=Δφ1 +Δφ2 0,14 ( 0,14 ) 0 ,
как и следовало ожидать, угол поворота в заделке В равен нулю.
113
По полученным значениям построим эпюры изменения по длине вала крутящих моментов Mкр, касательных напряжений τmax, относительных углов
закручивания θ и абсолютных углов поворота φ сечений (рис. 3.8, в, г, д, е).
2–3. Проверка прочности и жёсткости вала
Укажем наибольшие по абсолютной величине значения напряжений и углов закручивания:
τmax = 30 МПа; θmax = 1,08 /м; φmax = 0,14 .
Сделаем выводы о прочности и жёсткости вала. Для нашего примера:
τmax = 30 МПа < [τ] = 100 MПa;
θmax = 1,08 /м < [θ] = 2 /м; φmax = 0,14 < [φ] = 0,5 ,
значит, прочность и жёсткость вала обеспечены.
114
