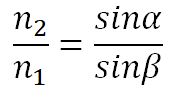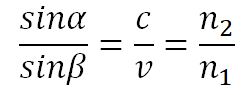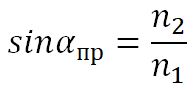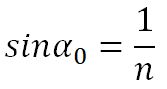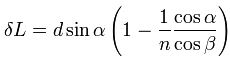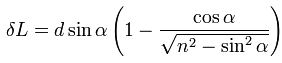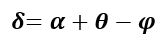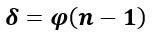Пусть луч
![]()
падает на одну из гранен призмы. Преломившись в точке
![]()
, луч пойдет по направлению
![]()
и, вторично преломившись в точке
![]()
, выйдет из призмы в воздух (рис. 189). Найдем угол
![]()
, на который луч, пройдя через призму, отклонится от первоначального направления. Этот угол мы будем называть углом отклонения. Угол между преломляющими гранями, называемый преломляющим углом призмы, обозначим
![]()
.

Рис. 189. Преломление в призме
Из четырехугольника
![]()
, в котором углы при
![]()
и
![]()
прямые, найдем, что угол
![]()
равен
![]()
. Пользуясь этим, из четырехугольника
![]()
находим
![]()
.
Отсюда
![]()
. (86.1)
Угол
![]()
, как внешний угол в треугольнике
![]()
, равен
![]()
, (86.2)
где
![]()
— угол преломления в точке
![]()
, а
![]()
— угол падения в точке
![]()
луча, выходящего из призмы. Далее, пользуясь законом преломления, имеем
![]()
, (86.3)
![]()
. (86.4)
С помощью полученных уравнений, зная преломляющий угол призмы
![]()
и показатель преломления
![]()
, мы можем при любом угле падения
![]()
вычислить угол отклонения
![]()
.
Особенно простую форму получает выражение для угла отклонения в том случае, когда преломляющий угол призмы
![]()
мал, т. е. призма тонкая, а угол падения
![]()
невелик; тогда угол
![]()
также мал. Заменяя приближенно в формулах (86.3) и (86.4) синусы углов самими углами (в радианах), имеем
![]()
.
Подставляя эти выражения в формулу (86.1) и пользуясь (86.2), находим
![]()
. (86.5)
Этой формулой, справедливой для тонкой призмы при падении на нее лучей под небольшим углом, мы воспользуемся в дальнейшем.
Обратим внимание, что угол отклонения луча в призме зависит от показателя преломления вещества, из которого сделана призма. Как мы указывали выше, показатель преломления для разных цветов света различен (дисперсия). Для прозрачных тел показатель преломления фиолетовых лучей наибольший, затем следуют лучи синие, голубые, зеленые, желтые, оранжевые, и, наконец, красные, которые имеют наименьший показатель преломления. В соответствии с этим угол отклонения
![]()
для фиолетовых лучей наибольший, для красных — наименьший, и луч белого цвета, падающий на призму, по выходе из нее окажется разложенным на ряд цветных лучей (рис. 190 и рис. I на цветном форзаце), т. е. образуется спектр лучей.
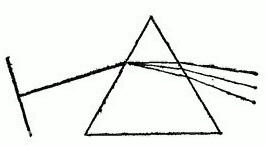
Рис. 190. Разложение белого света при преломлении в призме. Падающий пучок белого света изображен в виде фронта с перпендикулярным к нему направлением распространения волны. Для преломленных пучков показана только направления распространения волн
18.
Поместив экран позади куска картона, в котором проделано маленькое отверстие, можно получить на этом экране изображение источники. При каких условиях изображение на экране будет отчетливое? Объясните, почему изображение получается перевернутым?
19.
Докажите, что пучок параллельных лучей остается таким же после отражения от плоского зеркала

Рис. 191. К упражнению 27. Если чашка пустая, глаз не видит монеты (а), если же чашка наполнена водой, то монета видна (б). Палка, погруженная одним концом в воду, кажется сломанной (в). Мираж в пустыне (г). Как рыба видит дерево и ныряльщика (д)
20.
Чему равен угол падения луча, если луч падающий и луч отраженны» образуют угол
![]()
?
21.
Чему равен угол падения луча, если луч отраженный и луч преломленный образуют угол
![]()
? Показатель преломления второй среды относительно первой равен
![]()
.
22.
Докажете обратимость направления световых лучей для случая отражения света.
23.
Можно ли придумать такую систему зеркал и призм (линз) через которую один наблюдатель видел бы второго наблюдателя, а второй наблюдатель не видел бы первого?
24.
Показатель преломления стекла относительно воды равен 1,182: показатель преломления глицерина относительно воды равен 1.105. Найдите показатель преломления стекла относительно глицерина.
25.
Найдите предельный угол полного внутреннего отражения для алмаза на границе с водой.
26.
найдите смещение луча при прохождении его через плоскопараллельную пластинку из стекла с показателем преломления, равным 1,55, если угол падения
![]()
, а толщина пластинки равна
![]()
27.
Пользуясь законами преломления и отражения, объясните явления, показанные на рис. 191
«Никто
не зажигает свечу, чтобы хранить
ее
за дверью, ибо свет затем и существует,
чтобы
светить, открывать людям глаза,
показывать
какие вокруг чудеса»
П.
Коэльо
В
данной теме рассмотрим еще один важный закон геометрической оптики — закон
преломления света. А также рассмотрим общие принципы решения задач по
данной теме. В рамках прошлой темы говорилось об отражении света.
Отражение
— это изменение направления волнового фронта на
границе двух сред с разными свойствами, при этом волновой фронт возвращается в
среду, из которой он пришёл.
Нами
был сформулирован общий принцип распространения волн любой природы — принцип
Гюйгенса, согласно которому каждая точка среды, которой достиг фронт волны,
становится источником вторичных сферических волн.
Из
принципа Гюйгенса были выведены законы отражения света. Первый
закон гласит о том, что луч падающий, луч отраженный и перпендикуляр,
восставленный в точке падения луча, лежат в одной плоскости. Согласно второму
закону: угол падения равен углу отражения.
Известно
что, одновременно с отражением волн на границе раздела сред, как правило,
происходит и преломление волн.
Что
же такое преломление? Преломление—
это изменение направления распространения света, возникающее на границе раздела
двух прозрачных сред или в толще среды с непрерывно изменяющимися свойствами.
Угол
между преломленным лучом и перпендикуляром, восставленным к границе раздела
двух сред в точке падения луча, мы будем называть углом преломления.
Преломление
света на границе двух сред даёт парадоксальный зрительный эффект: пересекающие
границу раздела прямые предметы в более плотной среде выглядят образующими больший
угол с нормалью к границе раздела (то есть преломлёнными «вверх»); в то время
как луч, входящий в более плотную среду, распространяется в ней под меньшим
углом к нормали (то есть преломляется «вниз»). Этот же оптический эффект
приводит к ошибкам в визуальном определении глубины водоёма, которая всегда
кажется меньше, чем есть на самом деле.
А
преломление света в земной атмосфере приводит к тому, что мы наблюдаем восход
Солнца несколько раньше, а закат несколько позже, чем это имело бы место при
отсутствии атмосферы.
Первые
упоминания о преломлении света в воде и стекле встречаются в труде Клавдия
Птолемея «Оптика», вышедшем в свет во втором веке нашей эры. А непосредственно
сам закон преломления света был открыт опытным путем голландским ученым
Виллебордом Снеллиусом в 1621 году. Однако результаты многочисленных
экспериментов по оптике им опубликованы не были. Позже, после смерти ученого,
они были обнаружены в архивах Рене Декартом, который использовал их при
написании своих «Рассуждений о методе …» в приложении “Диоптрика” в
1637 году.
После
открытия Снеллиуса несколькими учеными была выдвинута гипотеза о том, что преломление
света обусловлено изменением его скорости при переходе через границу двух сред.
Справедливость этой гипотезы была подтверждена теоретическими доказательствами,
выполненными независимо друг от друга французским математиком Пьером Ферма в
1662 году и голландским физиком Христианом Гюйгенсом в 1690 году.
Рассмотрим,
что будет происходить с плоской световой волной, после её преломления на
границе раздела однородных изотропных и прозрачных сред. При этом, как и в
случае с отражением света, не забудем о том, что размеры поверхности раздела
намного больше длины волны падающего излучения. Для удобства, будем считать,
что скорость распространения света во второй среде меньше, чем в первой.
Фронт
падающей волны AB
будет перемещаться со скоростью по
направлению AA1.
К моменту времени, когда точка B
фронта волны достигнет границы раздела двух сред, вторичная волна, согласно
принципу Гюйгенса» пройдет расстояние A1A2
равное .
Фронт
волны, распространяющейся во второй среде, можно получить, проводя прямую
линию, касательную к полуокружности с центром в точке A1.
Из
построения видно:
Закон
преломления света: отношение синуса угла падения к
синусу угла преломления равно отношению скорости распространения света в первой
среде к скорости распространения света во второй среде.
В
курсе физики 9 класса вводились понятия абсолютного и относительного показателей
преломления среды. Абсолютным показателем преломления называется
отношение скорости распространения световой волны в вакууме к ее скорости
распространения в данной среде.
Относительный
показатель преломления показывает, во сколько раз скорость
света в первой по ходу луча среде отличается от скорости распространения света
во второй среде.
С
учётом данных определний, сформулируем закон преломления света в его
современном виде.
Первая
его часть очень напоминает закон отражения света. И так, луч падающий, луч
преломленный и перпендикуляр, восставленный к границе раздела двух сред в точке
падения луча, лежат в одной плоскости.
Отношение
синуса угла падения к синусу угла преломления есть величина постоянная для
данных двух сред, равная относительному показателю преломления второй по ходу
луча среды относительно первой — это вторая часть
закона преломления света.
Существуют
таблицы значений абсолютных показателей преломления для твердых, жидких и
газообразных веществ.
Из
таблицы видно, что из двух сред оптически более плотной считается та, у которой
показатель преломления больше (или та, в которой скорость света меньше). Отсюда
следует, что при переходе света из среды оптически менее плотной в среду
оптически более плотную угол преломления меньше угла падения.
Это
значит, что, попадая в среду оптически более плотную, луч отклоняется в
сторону перпендикуляра к границе двух сред. И наоборот, если происходит
переход луча из среды оптически более плотной в среду менее плотную, угол
преломления оказывается больше угла падения и луч прижимается к границе раздела
двух сред.
Помимо
этого, показатель преломления будет зависеть не только от скорости света в
данной среде, но и от физических свойств и состояния среды (т.е. от
температуры, плотности, упругости), а также от длины волны падающего света.
Рассмотрим,
что будет происходить со световой волной, если увеличивать угол ее падения. По
мере увеличения угла падения при его некотором значении a0
угол преломления станет равным 900, т.е. свет не будет попадать во
вторую среду.
Энергия
преломленной волны при этом станет равной нулю, а энергия отраженной волны
будет равна энергии падающей. Следовательно, начиная с этого угла падения, вся
световая энергия отражается от границы раздела этих сред. Это явление
называется полным отражением. А угол, при котором луч скользит вдоль
поверхности раздела сред, называется предельным углом полного отражения.
Он определяется из закона преломления света, при условии, что угол преломления
равен 900.
С
помощью закона преломления света можно рассчитать ход лучей в различных
оптических устройствах. Для примера, рассмотрим ход лучей в треугольной призме,
изготовленной из стекла или другого прозрачного материала.
Пусть
монохроматический свет падает на грань AB
стеклянной призмы, которая находится в воздухе (показатель преломления воздуха
будем считать равным единице). На рисунке изображены: падающий луч — S1O1,
угол падения — a1,
преломленный луч — O1O2,
и b1 — угол преломления.
Обратите внимание, что угол преломления меньше угла падения, так как свет
переходит из среды оптически менее плотной в оптически более плотную.
Пройдя
через призму, свет попадет на ее другую грань — AC.
Здесь он снова испытает преломление. На рисунке: a2
— угол падения, b2
— угол преломления. На данной грани свет переходит из оптически более плотной
среды в оптически менее плотную, поэтому угол преломления будет больше угла
падения. Грани BA
и CA, на которых
происходит преломление света, будем называть преломляющими гранями.
А
угол между этими гранями — преломляющим углом призмы (обычно его
обозначают буквой ).
Далее, угол образованный направлением луча, входящего в призму, и направлением
луча, выходящего из нее, называют углом отклонения. Грань, которая лежит
против преломляющего угла, мы будем называть основанием призмы.
Помимо
этого, еще необходимо знать некоторые соотношения для призмы:
Для
первой преломляющей грани закон преломления света запишется так:
Для
второй преломляющей грани закон преломления будет иметь вид:
Для
того, что бы найти преломляющий угол призмы, достаточно найти сумму угла
падения a2
и угла преломления b1.
А
чтобы определить угол отклонения луча, достаточно из предыдущей суммы
вычесть преломляющий угол призмы.
Таким
образом, получается, что если оптическая плотность вещества призмы будет
больше, чем окружающей среды, то луч света, проходящий через призму, отклонится
к ее основанию. Нетрудно показать, что если оптическая плотность окружающей
среды будет больше чем призмы, то луч света после прохождения через призму отклонится
к ее вершине.
Упражнения.
Задача
1. Под
каким углом должен упасть луч на стекло, показатель преломления которого 1,8,
чтобы преломленный луч оказался перпендикулярным отраженному?
Задача
2. Сечение
стеклянной призмы имеет форму равностороннего треугольника. Луч падает на одну
из граней перпендикулярно к ней. Вычислите угол между этим лучом и лучом,
вышедшим из призмы. Показатель преломления стекла равен 1,5.
Основные
выводы:
–
Преломлением называют изменение направления распространения света,
возникающее на границе раздела двух прозрачных сред или в толще среды с
непрерывно изменяющимися свойствами.
–
Закон преломления света, согласно которому луч
падающий, луч преломленный и перпендикуляр, восставленный к границе раздела
двух сред в точке падения луча, лежат в одной плоскости.
–
Отношение же синуса угла падения к синусу угла преломления есть величина
постоянная для данных двух сред, равная относительному показателю преломления
второй по ходу луча среды относительно первой.
Содержание:
Прохождение света через плоскопараллельные пластинки и призмы:
Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы.
Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые, создают различные оптические приборы. Рассмотрим отдельные элементы оптических приборов.
Плоскопараллельная пластинка
Рассмотрим ход луча в плоскопараллельной пластинке. На рисунке 77 показан ход светового луча в плоскопараллельной пластинке толщиной 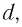
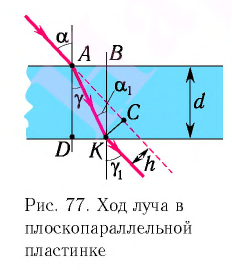
Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 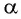 на первую границу, имеем:
на первую границу, имеем:
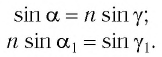
Здесь 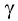 — угол преломления на первой границе,
— угол преломления на первой границе, 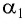 — угол падения луча на вторую границу,
— угол падения луча на вторую границу, 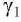 — угол преломления на второй границе,
— угол преломления на второй границе, 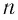 — абсолютный показатель преломления вещества пластинки.
— абсолютный показатель преломления вещества пластинки.
Накрест лежащие углы 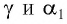 при параллельных прямых
при параллельных прямых 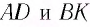 (перпендикулярах к первой и второй параллельным границам) равны, т. е.
(перпендикулярах к первой и второй параллельным границам) равны, т. е.  Следовательно,
Следовательно, 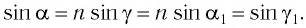 Откуда следует, что
Откуда следует, что
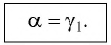
Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению на некоторое расстояние 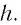
Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут также казаться смещенными.
Найдем, от каких параметров пластинки зависит смещение 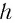 луча. Из
луча. Из 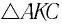 следует, что
следует, что
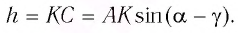
Из 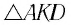 имеем:
имеем:
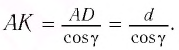
Отсюда:
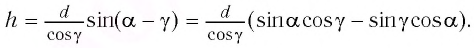
С учетом закона преломления 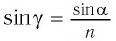 и тригонометрического тождества
и тригонометрического тождества 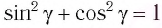 находим:
находим:
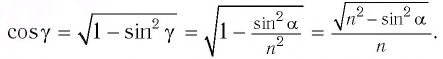
Расстояние 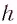 между направлениями входящего и выходящего лучей можно определить из соотношения
между направлениями входящего и выходящего лучей можно определить из соотношения
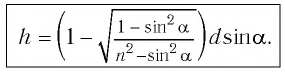
Как видно из соотношения (2), смещение 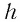 луча при данном угле падения
луча при данном угле падения 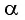 зависит от толщины
зависит от толщины 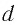 пластинки и ее показателя преломления
пластинки и ее показателя преломления 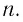
Трехгранная призма
Рассмотрим ход луча в трехгранной призме. Пусть световой луч 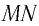 падает под углом
падает под углом 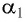 на боковую грань трехгранной призмы
на боковую грань трехгранной призмы 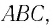 сечение которой показано на рисунке 78. Призма, изготовленная из вещества с абсолютным показателем преломления
сечение которой показано на рисунке 78. Призма, изготовленная из вещества с абсолютным показателем преломления 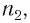 находится в среде с абсолютным показателем преломления
находится в среде с абсолютным показателем преломления 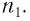 Угол
Угол 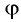 при вершине
при вершине 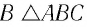 называется преломляющим углом призмы. Грани призмы, образующие преломляющий угол
называется преломляющим углом призмы. Грани призмы, образующие преломляющий угол 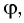 называются преломляющими. Грань, лежащая напротив преломляющего угла, называется основанием призмы.
называются преломляющими. Грань, лежащая напротив преломляющего угла, называется основанием призмы.
Пусть луч 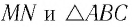 лежат в одной плоскости — плоскости листа книги. Из закона преломления света находим угол преломления
лежат в одной плоскости — плоскости листа книги. Из закона преломления света находим угол преломления 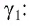
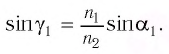
Если показатель призмы 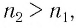 то преломленный луч
то преломленный луч 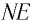 падает на вторую боковую грань призмы под углом
падает на вторую боковую грань призмы под углом 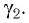 Полного отражения на второй преломляющей грани не происходит при условии
Полного отражения на второй преломляющей грани не происходит при условии 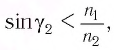 и луч выходит из призмы под углом
и луч выходит из призмы под углом 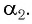 Его находим из закона преломления:
Его находим из закона преломления:
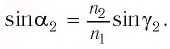
Отклонение от начального направления луча 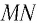 вследствие преломлений на гранях призмы определяется углом
вследствие преломлений на гранях призмы определяется углом 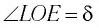 (см. рис. 78). Угол
(см. рис. 78). Угол 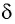 между направлениями входящего и выходящего лучей называется углом отклонения.
между направлениями входящего и выходящего лучей называется углом отклонения.
Рассмотрим 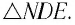 С учетом того, что
С учетом того, что 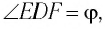 по теореме о внешнем угле треугольника находим:
по теореме о внешнем угле треугольника находим:
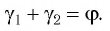
Применим эту же теорему к 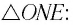
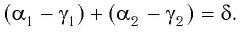
Из формул (5) и (6) определим связь угла падения 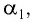 угла преломления
угла преломления 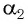 с преломляющим углом
с преломляющим углом 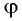 призмы и углом отклонения
призмы и углом отклонения 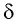 выходящего луча от начального направления:
выходящего луча от начального направления:
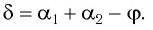
В результате получим систему уравнений (3), (4), (5), (7):
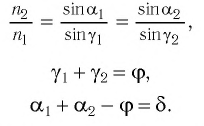
Система уравнений (8) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.
- Заказать решение задач по физике
Если угол падения 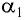 на грань призмы и преломляющий угол призмы
на грань призмы и преломляющий угол призмы 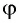 малы, то малыми будут и углы
малы, то малыми будут и углы 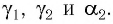 Поэтому в законах преломления (3) и (4) отношение синусов можно заменить отношением углов, выраженных в радианах, т. е.:
Поэтому в законах преломления (3) и (4) отношение синусов можно заменить отношением углов, выраженных в радианах, т. е.:
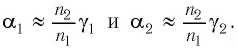
Подставляя полученные выражения для 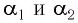 в соотношение (7), находим:
в соотношение (7), находим:
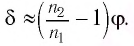
Из соотношения (9) следует, что, во-первых: чем больше преломляющий угол 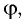 тем больше угол отклонения
тем больше угол отклонения 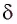 лучей призмой; во-вторых, угол отклонения
лучей призмой; во-вторых, угол отклонения 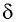 лучей увеличивается с ростом абсолютного показателя преломления
лучей увеличивается с ростом абсолютного показателя преломления 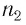 вещества призмы. Как видно из рисунка 78, луч света, проходя через трехгранную призму, отклоняется к ее утолщенной части, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды
вещества призмы. Как видно из рисунка 78, луч света, проходя через трехгранную призму, отклоняется к ее утолщенной части, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды 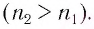
Пример решения задачи
Определите наименьший преломляющий угол 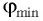 стеклянной призмы, находящейся в воздухе, при котором луч, падающий нормально на грань призмы, не выйдет через ее вторую боковую грань (рис. 79). Показатель преломления стекла призмы
стеклянной призмы, находящейся в воздухе, при котором луч, падающий нормально на грань призмы, не выйдет через ее вторую боковую грань (рис. 79). Показатель преломления стекла призмы 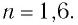
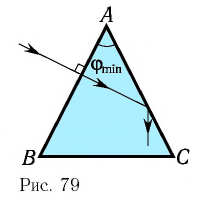
Дано:
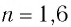
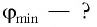
Решение:
Запишем условие полного отражения на боковой грани 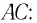
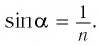
Вследствие того, что 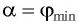 как углы с взаимно перпендикулярными сторонами:
как углы с взаимно перпендикулярными сторонами:
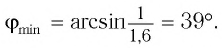
Ответ: 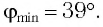
- Поляризация света
- Линзы в физике
- Глаз как оптическая система
- Звук в физике и его характеристики
- Электромагнитная природа света
- Интерференция света
- Дифракция света
- Принцип Гюйгенса — Френеля
Принцип Гюйгенса:
Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.
Закон отражения:
- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения;
- угол падения α равен углу отражения γ:
α = γ
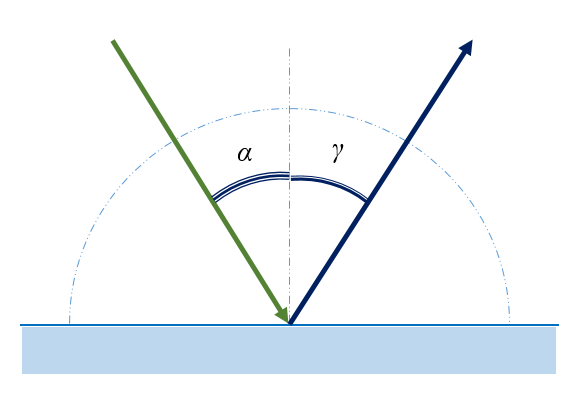
Вывод на основе принципа Гюйгенса:
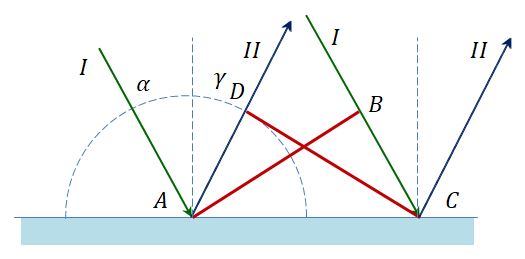
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.
Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.
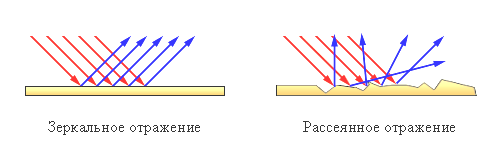
Закон преломления (закон Снелиуса):
- луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости;
- отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред.
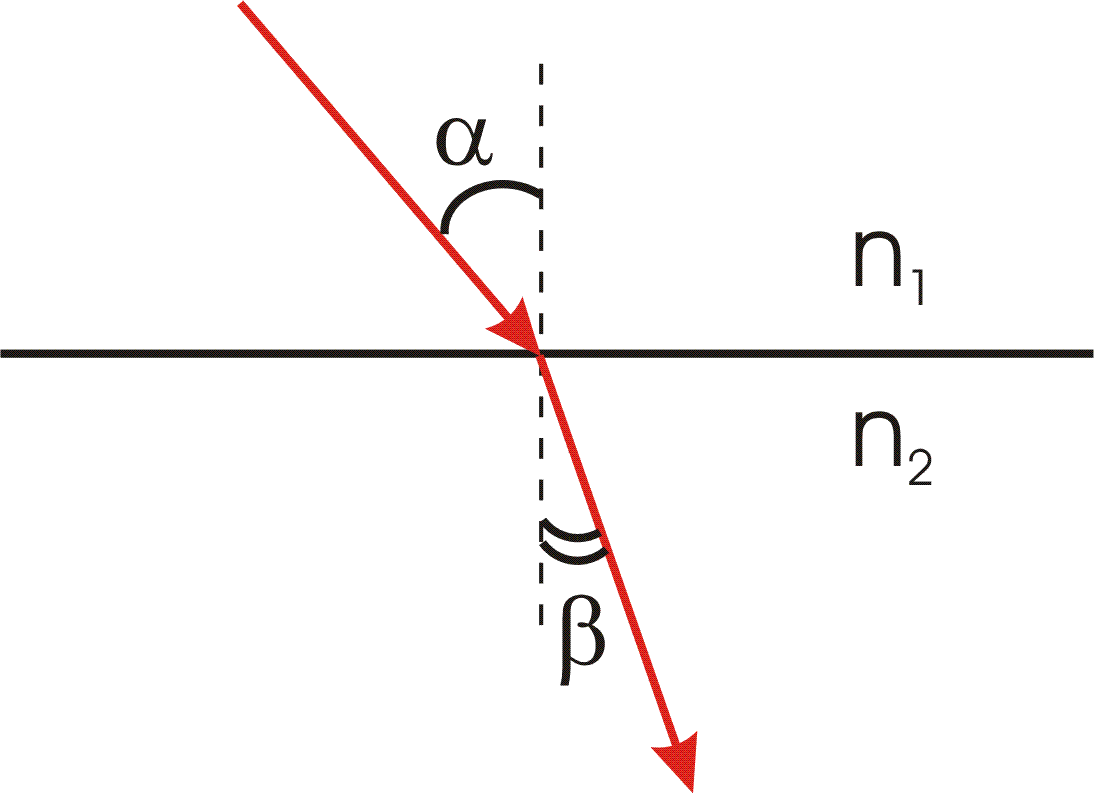

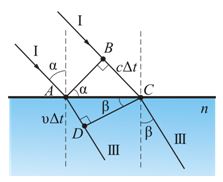
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.
Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что
 , т.е.
, т.е.  .
.
Отсюда следует закон Снелиуса:
Принцип Ферма: свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.
Покажем применение этого принципа к решению той же задачи о преломлении света.
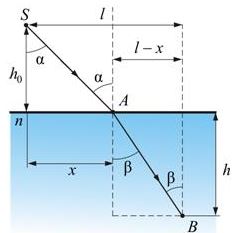
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела
В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:
 .
.
Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:
 ,
,
отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса:  .
.
Следствия из принципа Ферма:
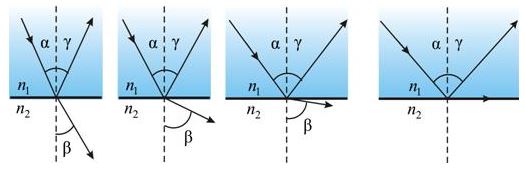
1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.
2. Если свет распространяется из среды с большим показателем преломления n1 (оптически более плотной) в среду с меньшим показателем преломления n2 (оптически менее плотной) ( n1 > n2 ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:
3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = αпр) угол преломления не окажется равным π/2.
Полное отражение
Угол αпр называется предельным углом полного отражения. При углах падения α > αпр весь падающий свет полностью отражается.
По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.
Если α = αпр , то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего.
Таким образом, при углах падения в пределах от αпр до π/2, луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
В случае, если вторая среда – воздух

Преломление света в плоскопараллельной пластине
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величинуδL относительно исходного луча
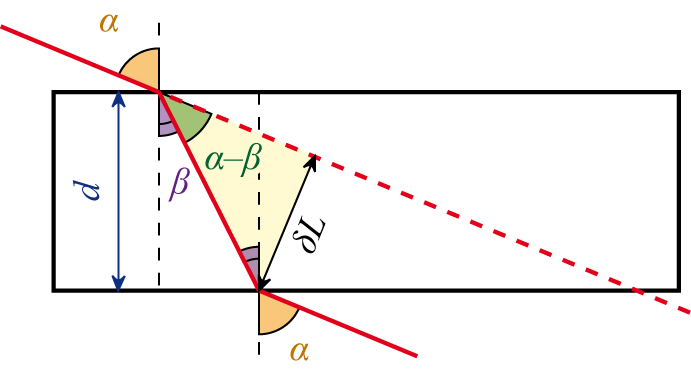
Величина смещения в плоскопараллельной пластине
Величина сдвига луча света δL зависит:
- от угла падения света α,
- от толщины пластины d,
- от показателя преломления вещества, из которого изготовлена плоскопараллельная пластина n.
C увеличением любого из этих параметров смещение луча света увеличивается.
Смещение луча можно выразить через угол падения
Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:
- угол падения равен нулю: α = 0,
- относительный показатель преломления равен единице (преломления не происходит): n = 1 ,
- толщина пластины равна нулю: d = 0
Ход луча через треугольную призму
Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.
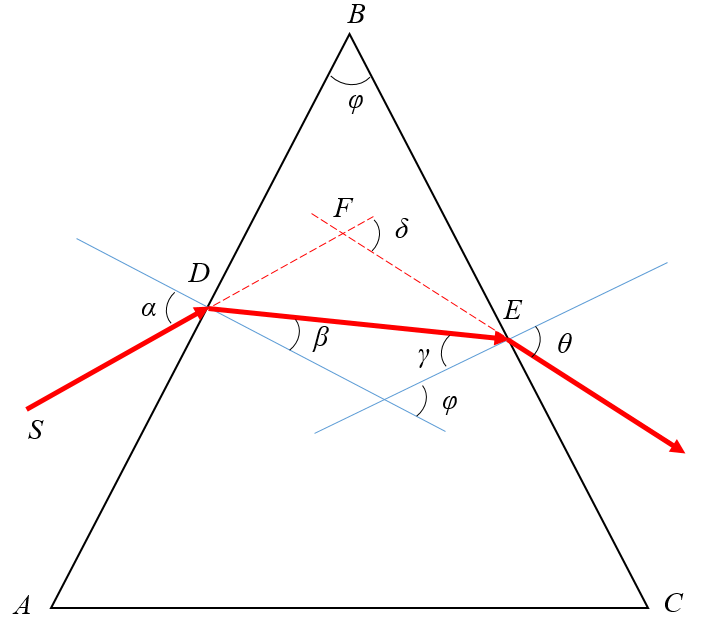
На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.
Если световой луч падает на преломляющую грань призмы под произвольным углом, то угол отклонения луча призмой определяется формулой
Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярнопреломляющей грани призмы), то угол отклонения луча призмой определяется формулой
Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.
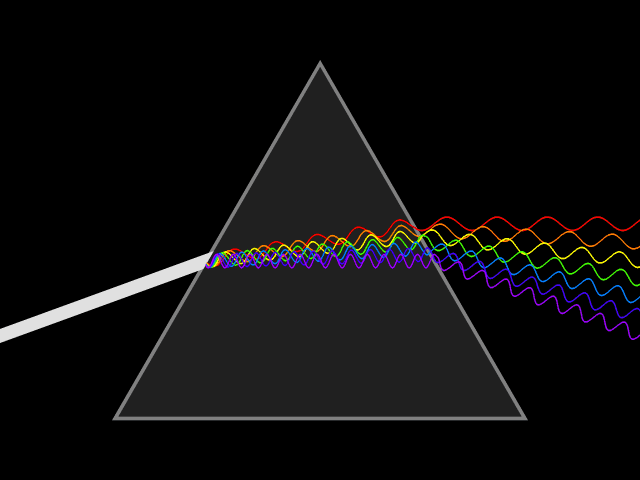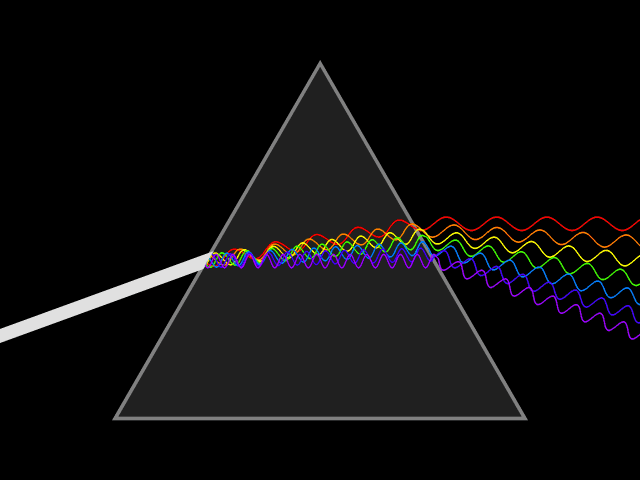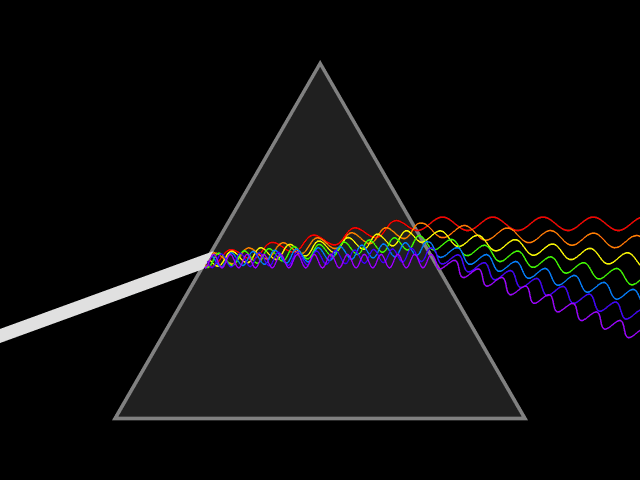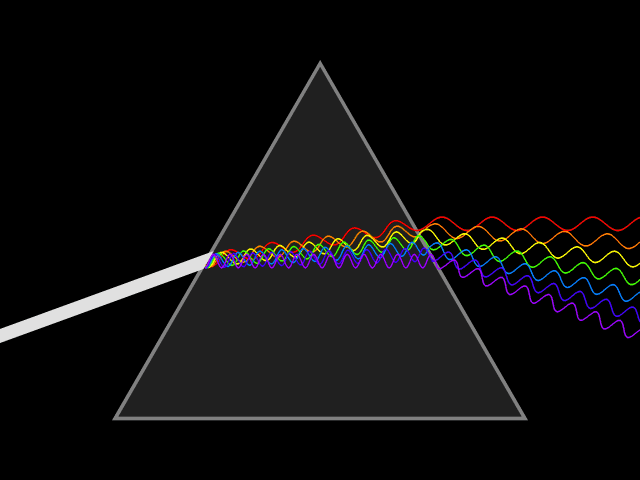
Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.


Условие задачи:
Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°. Угол падения луча на грань призмы равен 30°, а показатель преломления вещества призмы равен 1,5.
Задача №10.3.38 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(varphi=60^circ), (alpha=30^circ), (n_1=1,5), (theta-?)
Решение задачи:
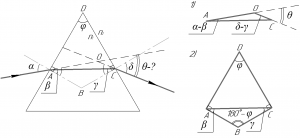 Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Сделаем к этой задаче рисунок, без него решить задачу невозможно. В задаче очень много геометрии и практически нет физики. Итак, начнем.
Рассмотрим треугольник AOC (смотрите рисунок 1). Искомый угол (theta) является смежным для этого треугольника, поэтому справедливо:
[theta = left( {alpha – beta } right) + left( {delta – gamma } right)]
[theta = alpha + delta – left( {beta + gamma } right);;;;(1)]
Далее рассмотрим четырёхугольник ABCD (смотрите рисунок 2). В этом четырехугольнике два угла – прямые, поэтому угол ABC равен (left( {180^circ – varphi } right)). На этом рисунке теперь рассмотрим треугольник ABC. Сумма углов любого треугольника равна 180°, поэтому будет верно записать:
[beta + gamma + left( {180^circ – varphi } right) = 180^circ ]
[varphi = beta + gamma ;;;;(2)]
Тогда уравнение (1) примет вид:
[theta = alpha + delta – varphi ;;;;(3)]
Чтобы найти угол преломления (delta), запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin gamma = {n_2}sin delta ]
Здесь (gamma) и (delta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_2) равен 1. Тогда:
[sin delta = frac{{{n_1}sin gamma }}{{{n_2}}}]
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin gamma } right)]
Из равенства (2) также следует, что (gamma = varphi – beta), поэтому:
[delta = arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – beta } right)} right);;;;(4)]
Чтобы найти угол преломления (beta), опять запишем закон преломления света:
[{n_2}sin alpha = {n_1}sin beta ]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Тогда:
[sin beta = frac{{{n_2}sin alpha }}{{{n_1}}}]
[beta = arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)]
Полученное выражение подставим в (4):
[theta = alpha – varphi + arcsin left( {frac{{{n_1}}}{{{n_2}}}sin left( {varphi – arcsin left( {frac{{{n_2}sin alpha }}{{{n_1}}}} right)} right)} right)]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[theta = 30^circ – 60^circ + arcsin left( {frac{{1,5}}{1}sin left( {60^circ – arcsin left( {frac{{1 cdot sin 30^circ }}{{1,5}}} right)} right)} right) = 47,1^circ ]
Ответ: 47,1°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.37 Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает
10.3.39 Луч света входит в стеклянную призму под углом π/6 и выходит из призмы в воздух
10.3.40 Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды