Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
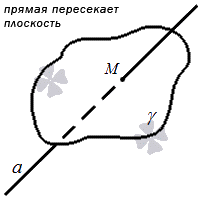
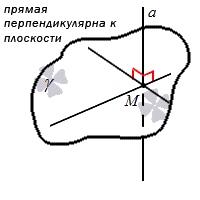
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
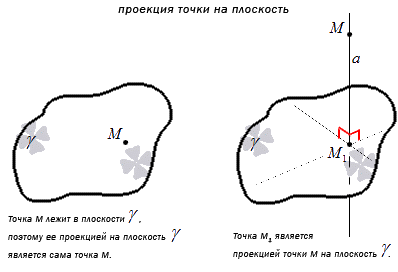
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ, проходящей через точку M, при условии, что она не принадлежит плоскости γ.
Проекция прямой а на плоскость γ – это множество проекций всех точек заданной прямой на плоскость.
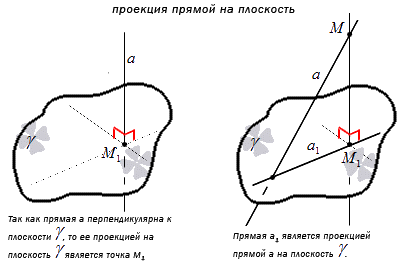
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
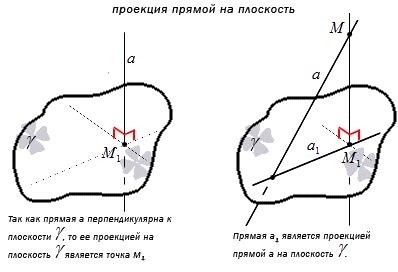
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
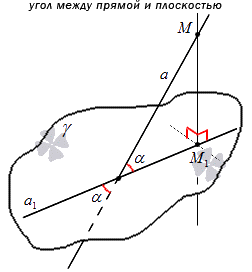
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
Если в трехмерном пространстве вводится прямоугольная система координат Охуz, тогда в ней задается прямая a, пересекающая плоскость γ в точке M, причем она не перпендикулярна плоскости. Необходимо найти угол α, находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат Охуz задается прямая a, которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости γ соответствует уравнение плоскости и нормальный вектор плоскости. Тогда a→=(ax, ay, az) является направляющим вектором заданной прямой a, а n→(nx, ny, nz) – нормальным вектором для плоскости γ. Если представить, что у нас имеются координаты направляющего вектора прямой a и нормального вектора плоскости γ, тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов a→ и n→, исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
Необходимо отложить векторы a→ и n→, начиная от точки пересечения прямой a с плоскостью γ. Существуют 4 варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все 4 вариации.
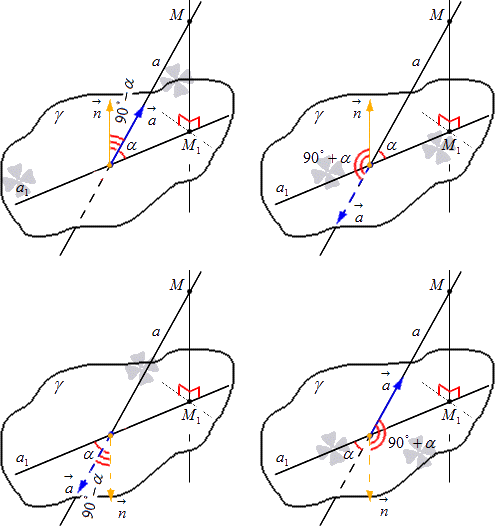
Отсюда получаем, что угол между векторами a→ и n→ имеет обозначение a→, n→^ и является острым, тогда искомый угол α , располагающийся между прямой и плоскостью, дополняется, то есть получаем выражение вида a→, n→^=90°-α. Когда по условию a→, n→^>90°, тогда имеем a→, n→^=90°+α.
Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы
cosa→, n→^=cos 90°-α, a→, n→^<90°cosa→, n→^=cos 90°+α, a→, n→^>90°
Необходимо использовать формулы приведения для упрощения выражений. Тогда получим равенства вида cosa→, n→^=sin α, a→, n→^<90°cosa→, n→^=-sin α, a→, n→^>90°.
Проведя преобразования, система приобретает вид sin α=cosa→, n→^, a→, n→^<90°sin α=-cosa→, n→^, a→, n→^>90°⇔sin α=cosa→, n→^, a→, n→^>0sin α=-cosa→, n→^, a→, n→^<0⇔⇔sin α=cosa→, n→^
Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.
Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле
sin α=cosa→, n→^=a→, n→^a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2
Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида
α=arcsina→, n→^a→·n→=arcsinax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы cos α=1-sin α.
Выполним решение нескольких подобных примеров для закрепления материала.
Найти угол, синус, косинус угла, образованного прямой x3=y+1-2=z-116 и плоскостью 2x+z-1=0.
Решение
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что a→=(3, -2, 6) является направляющим вектором прямой x3=y+1-2=z-116.
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости 2x+z-1=0 нормальный вектор имеет вид n→=(2, 0, 1).
Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов a→ и b→ в заданную формулу. Получаем выражение вида
sin α=cosa→, n→^=a→, n→^a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2==3·2+(-2)·0+6·132+(-2)2+62·22+02+12=1275
Отсюда найдем значение косинуса и значение самого угла. Получим:
cos α=1-sin α=1-12752=10175
Ответ: sin α=1275, cos α=10175, α=arccos10175=arcsin1275.
Имеется пирамида, построенная при помощи значений векторов AB→=1, 0, 2, AC→=(-1, 3, 0), AD→=4, 1, 1. Найти угол между прямой AD и плоскостью АВС.
Решение
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой AD направляющий вектор имеет координаты AD→=4, 1, 1.
Нормальный вектор n→, принадлежащий плоскости АВС, является перпендикулярным вектору AB→ и AC→. Это подразумевает то, что нормальным вектором плоскости АВС можно считать векторное произведение векторов AB→ и AC→. Вычислим это по формуле и получим:
n→=AB→×AC→=i→j→k→102-130=-6·i→-2·j→+3·k→⇔n→=(-6, -2, 3)
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:
α=arcsinAD→, n→^AD→·n→=arcsin4·-6+1·-2+1·342+12+12·-62+-22+32=arcsin23212
Ответ: arcsin23212.
Построение угла между прямой и плоскостью
Углом между прямой и плоскостью называется угол, который прямая образует со своей проекцией на данную плоскость. Его величина может быть определена графически в соответствии с приведенным ниже алгоритмом.
Алгоритм построения
- Из произвольной точки, взятой на прямой, проводят перпендикуляр к заданной плоскости.
- Способом вращения вокруг линии уровня определяют величину угла β° между построенным перпендикуляром и прямой.
- Вычисляют искомый угол α° = 90° – β°.
Задача 1
Рассмотрим, как осуществляется описанный нами алгоритм на практике. На рисунке ниже приведены построения, с помощью которых вычислен угол α° между прямой a и плоскостью γ, заданной параллельными прямыми c и d.

Решение
- Строим проекции фронтали f и горизонтали h плоскости γ. Для этого используем вспомогательные точки 1 и 2, 3 и 4.
- Из произвольной точки K, лежащей на прямой a, опускаем перпендикуляр b на плоскость γ. Как видно на рисунке, проекция b’⊥h’, а b”⊥f”.
- Определяем величину угла β° между прямыми a и b способом поворота вокруг линии уровня. Для этого сначала строим горизонталь h1 и перпендикулярно её проекции h’1 проводим луч K’O’. Центр поворота O’ = K’O’ ∩ h’1.
Определяем радиус вращения R как гипотенузу прямоугольного треугольника K0K’O’, катет которого K0K’ равен величине ZO – ZK. После этого по дуге окружности переводим точку K0 в положение K’1, как это показано на рисунке выше. Угол β° находится при вершине K’1. - Вычисляем значение искомого ∠α° = 90° – ∠β°.
Задача 2
В данном примере прямая e занимает общее положение, а плоскость γ задана следами. В отличие от предыдущей задачи здесь нет необходимости достраивать горизонталь и фронталь, поскольку их роль выполняют следы h0γ и f0γ.

Решение
- На прямой e возьмем произвольную точку N и из неё опустим перпендикуляр m на плоскость γ. Проекцию m’ нужно провести перпендикулярно h0γ, а m”⊥f0γ соответственно.
- Определяем величину угла β° между прямыми m и е способом вращения вокруг линии уровня, в качестве которой в нашей задаче была использована горизонталь h.
- Вычисляем величину искомого ∠α° = 90° – ∠β°.
Похожие задачи:
- Определение натуральной величины угла;
- Построение угла между плоскостями.
Угол между прямой и плоскостью
Навигация по странице:
- Определение угла между прямой и плоскостью
- Формула для вычисления угла между прямой и плоскостью
- Вывод формулы вычисления угла между прямой и плоскостью
- Примеры задач на вычисление угла между прямой и плоскостью
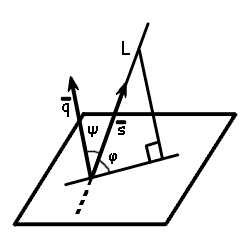
Определение.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Формула вычисления угла между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Пример вычисления угла между прямой и плоскостью
Пример 1.
Найти угол между прямой
| x – 4 | = | y + 2 | = – | z – 6 |
| 2 | 6 | 3 |
и плоскостью x – 2y + 3z + 4 = 0.
Решение.
Из уравнения прямой найдем направляющий вектор прямой
s = {2; 6; -3}
Из уравнения плоскости найдем вектор нормали плоскости
q = {1; -2; 3}
Воспользовавшись формулой, найдем угол между прямой и плоскостью
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
=
| 2 – 12 – 9 |√4 + 36 + 9 · √1 + 4 + 9
=
|-19|√49 · √14
=
197√14
Ответ: sin φ = 197√14.
Угол
прямой линии с плоскостью проекции
определяется как угол, составленный
прямой с ее проекцией на этой плоскости.
Этот угол входит в тот же прямоугольный
треугольник, который строят для
определения Н.В. отрезка.
Следом
прямой линии называется точка, в которой
прямая пересекается с плоскостью
проекций (так как след – точка, принадлежащая
одной из плоскостей проекций, то одна
из её координат должна быть равна
нулю).
Горизонтальный
след – точка пересечения прямой с
горизонтальной плоскостью проекций.
Фронтальный
след – точка пересечения прямой с
фронтальной плоскостью проекций.
Профильный
след
– точка пересечения прямой с профильной
плоскостью проекций.
7.Проекции плоских углов:
1.Если пл-ть в которой расположен некоторый угол перпендик.К пл-ти проекции,то он проецируется на эту пл-ть в виде прямой.
2.Если стороны угла // пл-ти проекции,то угол проецируется в свою величину.
3.Если пл-ть прямого угла не перпендикулярна к пл-ти проекции и хотя бы одна сторона угла // этой пл-ти, то прямой угол проецируется на пл-ть в виде прямого же угла.
4.Если проекция плоского угла представляет собой прямой угол,то проецируемый угол будет прямым лишь при условии что хотя бы одна из сторон угла параллельна пл-ти проекции
5.Если проекция некоторого угла у которого одна сторона // пл-ти проекции представляет собой прямой угол, то проецируемый угол тоже прямой
10.Особые линии плоскости
Прямые
уровня – это
прямые, принадлежащие плоскости и
параллельные какай – либо плоскости
проекций. Эти прямые называют прямыми
уровня, так как они принадлежат плоскости
уровня. Существует три вида прямых
уровня:
h
– горизонталь плоскости – прямая
принадлежащая данной плоскости и ||
плоскости проекций 1;
f
– фронталь плоскости – прямая принадлежащая
данной плоскости и || плоскости проекций
2;
w
– профильная прямая плоскости – прямая
принадлежащая данной плоскости и ||
плоскости проекций 3.
Прямая,
принадлежащая плоскости и
![]()
к
горизонтали, фронтали или профильной
прямой, называется линией наибольшего
наклона плоскости к плоскости проекций
П1,
П2
или П3.
Линию наибольшего наклона к плоскости
проекций П1
называют линией наибольшего ската.
5.Взаимное положение прямых в пространстве
Две
прямые в пространстве могут пересекаться,
скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися
прямыми называются такие прямые, которые
имеют одну общую точку.
2. Параллельные прямые
параллельные
прямые – прямые, пересекающиеся в
несобственной точке (прямые, лежащие
в одной плоскости и пересекающиеся в
бесконечно удаленной точке).
3.Скрещивающиеся прямые
Скрещивающиеся
прямые – это прямые, которые не // и не
пересекаются между собой.
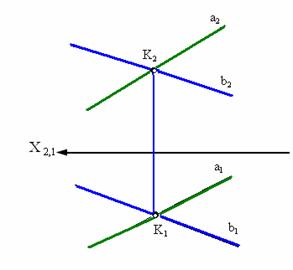
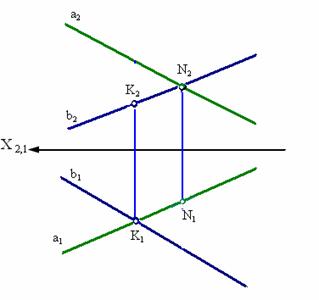
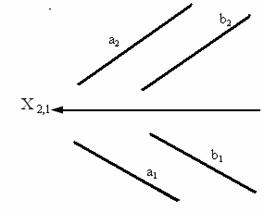
6.Скрещивающиеся прямые. Видимость скрещ.Прямых.
Скрещивающиеся
прямые – прямые, которые не // и не
пересекаются между собой.
Точка
пересечения одноименных проекций
скрещ. прямых представляет собой
проекции двух точек из которых одна
принадлежит первой, а другая – второй
из этих скрещ. прямых.
Если
видно что на одной проекции точки
совпадают, а на другой четко видно, что
проекции принадлежат разным отрезкам,
нужно определять видимость. Точка
которая находится дальше от плоскости
проекции (т.1) и закрывает собой другую
точку(т.2) будет видимой. => т.2 невидимая.
Такие точки называются конкурирующими.
8.
Способы
задания пл-ти:
1.3-мя
точками не лежащими на одной прямой.
2.Прямой и точкой, вне этой прямой.
3.Пересекающимися прямыми.
4.Двумя //прямыми
5.Любой плоской фигурой.
6.Параметрами
7.Следами
Следы
пл-ти – прямые по которым некоторая
пл-ть пересекает пл-ти проекций.
|
9.положение |
В
зависимости от положения плоскости по
отношению к плоскостям проекций она
может занимать как общее, так и частные
положения.
Плоскость
не перпендикулярная ни одной плоскости
проекций называется плоскостью
общего положения.
Такая плоскость пересекает все плоскости
проекций (имеет три следа: – горизонтальный
;
фронтальный ;
профильный).
Плоскости,
перпендикулярные плоскостям проекций
– занимают частное положение в
пространстве и называются проецирующими.
В зависимости от того, какой плоскости
проекций перпендикулярна заданная
плоскость, различают:
1.Плоскость, перпендикулярная горизонтальной плоскости проекций ,называется горизонтально проецирующей плоскостью.
2. Плоскость, перпендикулярная профильной плоскости – профильно-проецирующая плоскость.
3. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.
4. Фронтальная плоскость – плоскость, параллельная фронтальной плоскости проекций.
5. Профильная плоскость – плоскость, параллельная профильной плоскости проекций
11.Линии наиб. Уклона и их применение.
Линией
наиб. уклона плоскости называется
прямая , принадлежащая этой плоскости
и перпендикулярная ее линиям уровня:
горизонтали h и фронтали f. На комплексном
чертеже гориз. проекция линии наиб.
уклона перпендикулярна гориз. проекции
горизонтали этой плоскости, а фронтальная
− фронтальной проекции фронтали.
Главным свойством этой линии наибольшего
уклона является то, что она образует с
горизонтальной плоскостью проекций
угол α°, равный углу наклона плоскости
к плоскости. Это свойство линии
наибольшего уклона используется для
определения углов наклона плоскостей
к плоскостям проекций.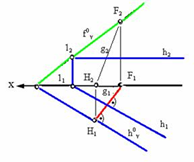
12. Прямая и точка в плоскости
В
пространстве прямая может либо
принадлежать плоскости, либо не
принадлежать плоскости. Это утверждение
справедливо и для точки. Прямая
принадлежит плоскости, если она проходит:
• Через
две точки, принадлежащие плоскости;
• Через
точку плоскости параллельно любой
прямой этой плоскости.
Точка
принадлежит плоскости, если она
принадлежит любой прямой в этой
плоскости.
25. Встречаются случаи, когда поверхности вращения пересекаются по двум плоским кривым – эллипсам. Это бывает тогда, когда поверхности двух тел вращения описаны около сфер.
если
две цилиндрические или конические, или
одна коническая, а другая цилиндрическая
поверхности описаны вокруг сферической
поверхности (и, следовательно, оси их,
пересекаясь, проходят через центр
сферы), то они пересекаются по плоским
кривым (эллипсам);
Пересечение
поверхностей вращения:
а) Конуса
с конусом;
б) Цилиндра
с конусом:
в) Тора
с тором;
26.Развертка поверхности многогранников
Разверткой
многогранной поверхности называется
плоская фигура, получаемая последовательным
совмещением всех граней поверхности
с плоскостью.
Так
как все грани многогранной поверхности
изображаются на развертке в натуральную
величину, построение ее сводится к
определению величины отдельных граней
поверхности – плоских многоугольников.
Существует
три метода построения развертки
многогранных поверхностей:
1. Метод треугольника.
2. Метод нормального сечения.
3. Метод раскатки.
27.Развертка поверхностей вращения
Развертка
– плоская фигура, в которую преобразуется
поверхность путем совмещения с плоскостью
без разрывов и складок.
К
развертываемым поверхностям относят
поверхности:
•многогранников;
•линейчатые
поверхности с параллельными или
пересекающимися образующими, а именно
– цилиндрические, конические и поверхности
с ребром возврата.
Развертки
многогранников относят к точным
разверткам. Поверхность называется
развертываемой на плоскость, если между
точками поверхности и плоскости можно
установить взаимно однозначное
соответствие, при котором:
•каждой
точке поверхности соответствует точка
на развертке;
•длины
соответствующих линий на поверхности
и на развертке равны между собой;
•замкнутая
линия на поверхности и соответствующая
ей линия на развертке ограничивают
одинаковую площадь;
•угол
между линиями на поверхности равен
углу между соответствующими им линиям
на развертке;
•отрезку
прямой линии на развертке соответствует
геодезическая линия поверхности,
кратчайшим путем соединяющая две точки
на данной поверхности
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Бонусы: вебинары из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ 14. Стереометрия. Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой — это первое видео раздела «Стереометрия», входящее в полный курс подготовки к ЕГЭ (о нем ниже).
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ №14. Стереометрия. Разбор варианта профильного ЕГЭ
Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
Об этом в нашем вебинаре в задаче о шестиугольной призме.
ЕГЭ 14 Стереометрия. Разбора задачи статграда, февраль 2021
Что проще: призма или пирамида? Хоть в призме и больше рёбер и граней, но с пирамидами справляться сложнее, причём прямо начиная с рисунка: все линии налезают друг на друга, ничего нигде не параллельно, в общем, лучше бы призму дали.
Но как только научились рисовать пирамиду, сразу всё стало проще: кругом одни треугольники, а как известно, фигур проще треугольника в геометрии найти не так-то просто 🙂
А если где прямые углы найдём, то вообще сказка.
Из этого видео вы узнаете, как правильно рисовать пирамиду и научитесь решать задачу №14 из февральского СтатГрада
