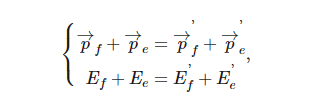Как найти угол рассеивания фотона

Как найти угол рассеивания фотона

Тема: Найти угол рассеяния фотона  (Прочитано 4424 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Найти угол рассеяния фотона, испытывающего соударение со свободным электроном, если изменение длины волны при рассеянии равно ∆λ =  3,62 пм.

« Последнее редактирование: 03 Апреля 2015, 06:21 от alsak »


Записан

Решение.
Изменение длины волны фотона при рассеянии его на электроне определяется по формуле:

[ Delta lambda ={lambda }’-lambda =frac{h}{mcdot c}cdot (1-cos alpha ), 1-cos alpha =frac{mcdot ccdot Delta lambda }{h},cos alpha =1-frac{mcdot ccdot Delta lambda }{h} (1) ]

Где: h = 6,62∙10-34 Дж∙с – постоянная Планка, m = 9,1∙10-31 кг – масса электрона, с = 3∙108 м/с – скорость света.
соsα = -0,49.
α = 119,3°.

« Последнее редактирование: 03 Апреля 2015, 06:21 от alsak »


Записан

Источник
Квантовая механика
  • Введение[en]
  • История[en]
    Математические основы

Основа

  • Классическая механика
  • Постоянная Планка
  • Интерференция
  • Бра и кет
  • Гамильтониан
  • Старая квантовая теория

Фундаментальные понятия

  • Квантовое состояние
  • Квантовая наблюдаемая
  • Волновая функция
  • Квантовая суперпозиция
  • Квантовая запутанность
  • Смешанное состояние
  • Измерение
  • Неопределённость
  • Принцип Паули
  • Дуализм
  • Декогеренция
  • Симметрия
  • Теорема Эренфеста
  • Туннельный эффект

Эксперименты

  • Опыт Дэвиссона — Джермера
  • Опыт Франка — Герца
  • Опыт Штерна — Герлаха
  • Опыт Юнга
  • Квантовый ластик
  • Квантовый ластик с отложенным выбором
  • Проверка неравенств Белла
  • Фотоэффект
  • Эффект Комптона

Формулировки

  • Представление Шрёдингера
  • Представление Гейзенберга
  • Представление взаимодействия
  • Представление фазового пространства
  • Матричная квантовая механика
  • Интегралы по траекториям
  • Диаграммы Фейнмана

Уравнения

  • Шрёдингера
  • Паули
  • Клейна — Гордона
  • Дирака
  • Швингера — Томонаги
  • фон Неймана
  • Блоха
  • Линдблада
  • Гейзенберга

Интерпретации

  • Копенгагенская
  • Теория скрытых параметров
    • Локальная[en]
  • Многомировая
  • Теория де Бройля — Бома

Развитие теории

  • Квантовая теория поля
  • Квантовая электродинамика
  • Теория Глэшоу — Вайнберга — Салама
  • Квантовая хромодинамика
  • Стандартная модель
  • Квантовая гравитация

Сложные темы

  • Релятивистская квантовая механика
  • Квантовая теория поля
  • Квантовая гравитация
  • Теория всего

Известные учёные

  • Планк
  • Эйнштейн
  • Шрёдингер
  • Гейзенберг
  • Йордан
  • Бор
  • Паули
  • Дирак
  • Фок
  • Борн
  • де Бройль
  • Ландау
  • Фейнман
  • Бом
  • Эверетт

См. также

  • История возникновения
  • Глоссарий[en]
  • ЭПР-парадокс
См. также: Портал:Физика

Эффе́кт Ко́мптона (ко́мптон-эффе́кт, ко́мптоновское рассе́яние) — упругое рассеяние фотона заряженной частицей, обычно электроном, названное в честь первооткрывателя Артура Холли Комптона. Если рассеяние приводит к уменьшению энергии, поскольку часть энергии фотона передаётся отражающемуся электрону, что соответствует увеличению длины волны фотона (который может быть рентгеновским или гамма-фотоном), то этот процесс называется эффектом Комптона. Обратное комптоновское рассеяние происходит, когда заряженная частица передаёт фотону часть своей энергии, что соответствует уменьшению длины волны кванта света.

Обнаружен американским физиком Артуром Комптоном в 1923 году в экспериментах с рентгеновским излучением[1][2]; за это открытие Комптон стал лауреатом Нобелевской премии по физике за 1927 год.

Эффект Комптона по природе подобен фотоэффекту — разница заключается в том, что при фотоэффекте фотон полностью поглощается электроном, тогда как при комптоновском рассеянии он только меняет направление движения и энергию[3].

Вступление[править | править код]

Рис. 1: Схема эксперимента Комптона. Комптоновское рассеяние происходит в графитовой мишени слева. Щель пропускает рентгеновские фотоны, рассеянные под выбранным углом. Энергия рассеянного фотона измеряется с помощью брэгговского рассеяния в кристалле справа в сочетании с ионизационной камерой; камера могла измерять только полную энергию, выделяемую с течением времени, а не энергию отдельных рассеянных фотонов

Комптоновское рассеяние является примером упругого рассеяния[4][5] света на свободной заряженной частице, где длина волны рассеянного света отличается от длины волны падающего излучения. В первоначальном эксперименте Комптона (см. Рис. 1) энергия рентгеновского фотона (≈17 кэВ) была намного больше, чем энергия связи атомного электрона, поэтому электроны можно было считать свободными после рассеяния. Величина, на которую изменяется длина волны света, называется комптоновским сдвигом. Хотя ядерное комптоновское рассеяние существует[6], комптоновское рассеяние обычно относится к взаимодействию, в котором участвуют только электроны атома.

Эффект наблюдал Артур Холли Комптон в 1923 году в Вашингтонском университете в Сент-Луисе и в последующие годы этот эффект подтвердил его аспирант Ю. Х. Ву. Комптон получил Нобелевскую премию по физике 1927 года за своё открытие.

Этот эффект демонстрирует, что свет не может быть объяснён исключительно как волновое явление[7]. Томсоновское рассеяние, следующее из классической теории рассеяния электромагнитных волн заряженными частицами, не может объяснить сдвиги в длине волны при низкой интенсивности, потому что классически свет должен быть достаточной интенсивности для того, чтобы электрическое поле ускоряло заряженную частицу до релятивистской скорости, вызывало отдачу из-за радиационного давления и связанный с ним доплеровский сдвиг рассеянного света[8], но эффект стал бы сколь угодно малым при достаточно низких интенсивностях света независимо от длины волны. Таким образом, свет ведёт себя так, как будто он состоит из частиц, что объясняет низкоинтенсивное комптоновское рассеяние. Или предположение, что электрон можно рассматривать как свободный, неверно, что приводит к фактически бесконечной массе электрона, равной массе ядра (см., например, комментарий ниже об упругом рассеянии рентгеновских лучей, вызванном этим эффектом). Эксперимент Комптона убедил физиков в том, что свет можно рассматривать как поток частицеподобных объектов (квантов, называемых фотонами), энергия которых пропорциональна частоте световой волны.

Рис.2: Фотон с длиной волны lambda падает слева и сталкивается с неподвижной мишенью, а новый фотон с длиной волны {displaystyle lambda '} рассеивается под углом theta к первоначальному направлению движения. Мишень отскакивает, унося зависящее от угла количество падающей энергии

Как показано на рис.2, взаимодействие между электроном и фотоном приводит к тому, что электрон получает часть энергии, а фотон с оставшейся энергией излучается в направлении, отличном от исходного, так что общий импульс системы также сохраняется. Если у рассеянного фотона ещё достаточно энергии, процесс может повториться. В этом сценарии электрон рассматривается как свободный или слабосвязанный. Экспериментальная проверка сохранения импульса в отдельных процессах комптоновского рассеяния Боте и Гейгером, а также Комптоном и Саймоном была важна для опровержения теории Бора — Крамерса — Слэтера, которая основывалась на старой квантовой теории.

Комптоновское рассеяние — один из трёх конкурирующих процессов при взаимодействии фотонов с веществом. При энергиях от нескольких эВ до нескольких кэВ, соответствующих спектру от видимого света до мягкого рентгеновского излучения, фотон может быть полностью поглощён, а его энергия может оторвать электрон от основного атома, процесс, известный как фотоэффект. Фотоны высокой энергии 1,022 МэВ и выше могут бомбардировать ядро и вызывать образование электрон-позитронной пары. Этот процесс называется рождением пар. Комптоновское рассеяние является наиболее важным процессом при взаимодействии в промежуточной области энергий.

Описание явления[править | править код]

К началу 20-го века исследования взаимодействия рентгеновских лучей с веществом шли полным ходом. Было замечено, что когда рентгеновские лучи известной длины волны взаимодействуют с атомами, рентгеновские лучи рассеиваются под углом theta и длина волны рассеянного кванта связана с theta . Хотя классический электромагнетизм предсказывал, что длина волны рассеянных лучей должна быть равна начальной длине волны[9], многочисленные эксперименты показали, что длина волны рассеянных лучей была больше (что соответствовало более низкой энергии), чем исходная длина волны.

В 1923 году Комптон опубликовал в Physical Review статью, в которой объяснил рентгеновский сдвиг, приписывая частицеподобный импульс световым квантам. Эйнштейн предложил световые кванты в 1905 году для объяснения фотоэффекта, но Комптон не основывался на работе Эйнштейна. Энергия световых квантов зависит только от частоты света. В своей статье Комптон вывел математическую связь между сдвигом длины волны и углом рассеяния рентгеновских лучей, предположив, что каждый рассеянный рентгеновский фотон взаимодействует только с одним электроном. Его статья завершается отчётом об экспериментах, которые подтвердили полученное им соотношение:

{displaystyle lambda '-lambda ={frac {h}{m_{e}c}}(1-cos {theta })~,}
где: lambda  — начальная длина волны,
{displaystyle lambda '} — длина волны после рассеяния,
h — постоянная Планка ,
m_e — масса покоя электрона,
c — скорость света
theta  — угол рассеяния.

Величина {displaystyle {frac {h}{m_{e}c}}} известна как комптоновская длина волны электрона; она равна 2,43⋅10-12 м. Сдвиг длины волны {displaystyle (lambda '-lambda )} равен по крайней мере нулю (theta =0°) и не более чем в два раза превышает комптоновскую длину волны электрона (theta =180°).

Комптон обнаружил, что у некоторых рентгеновских лучей не наблюдается сдвиг длины волны, несмотря на то, что они рассеиваются на большие углы; в каждом из этих случаев фотон не мог выбить электрон[9]. Таким образом, величина этого сдвига связана не с комптоновской длиной волны электрона, а с комптоновской длиной волны всего атома, которая может быть в 10000 раз меньше. Это известно как «когерентное» рассеяние на всём атоме, поскольку атом остается неповреждённым и не получает внутреннего возбуждения.

В первоначальных экспериментах Комптона, приведённых выше, непосредственно измерялся сдвиг длины волны. В современных экспериментах принято измерять энергии, а не длины волн рассеянных фотонов. Для данной энергии падающего кванта {displaystyle E_{gamma }=hc/lambda ,} энергия исходящего фотона в конечном состоянии, {displaystyle E_{gamma ^{prime }}}, задаётся как:

{displaystyle E_{gamma ^{prime }}={frac {E_{gamma }}{1+(E_{gamma }/m_{e}c^{2})(1-cos theta )}}~.}

Невозможность классического толкования[править | править код]

В классической электродинамике взаимодействие электрона с электромагнитной волной, при учёте только электрической составляющей, описывается следующим образом: под действием периодических возмущений, электрон начинает колебаться с той же частотой, что и набегающая волна, и излучать новые электромагнитные волны той же частоты.

Если учесть в том числе и магнитное поле, то движение электрона будет описываться сложным дифференциальным уравнением, и, в случае если поле достаточно сильное, чтобы разогнать электрон до релятивистских скоростей, электрон может начинать излучать на частотах, отличных от частоты начальной волны[10].

Однако ни в коем случае классическая теория не предполагает существование у электронов отдачи — волна распределена в пространстве и не может «сконцентрироваться» на одном электроне и выбить его из атома. Поэтому регистрация таких электронов точно указывает на неполноту классического описания, а именно, на корпускулярно-волновую природу света[11].

Квазиклассический подход позволяет получить только изменение длины волны рассеянного фотона. Для вычисления сечения рассеяния необходимо применить уравнения квантовой электродинамики. Такое распределение даёт Формула Клейна — Нишины.

При росте энергии фотона вероятность рассеяния постепенно уменьшается, причём вероятность рассеяния на большие углы уменьшается быстрее.

Угол рассеяния электрона отдачи отличается от угла рассеяния фотона, и, в случае рассеяния на свободном электроне, описывается уравнением[12]:

{displaystyle {mbox{tg}}phi ={frac {{mbox{ctg}}(theta /2)}{1+hnu /(m_{e}c^{2})}}~,}
где theta  — угол рассеяния фотона.

Вывод формулы рассеяния[править | править код]

Рис. 3: Энергии фотона при 500 кэВ и электрона после комптоновского рассеяния.

Фотон γ с длиной волны λ сталкивается с электроном e в атоме, который рассматривается как покоящийся. Столкновение заставляет электрон испытывать отдачу, и новый фотон γ‘ с длиной волны λ‘ отлетает под углом θ к первоначальному направлению движения фотона. (Далее e‘ — электрон после столкновения.) Комптон допускал возможность того, что взаимодействие иногда ускоряет электрон до скоростей, достаточно близких к скорости света, что требует применения специальной теории относительности Эйнштейна для правильного описания его энергии и импульса.

В заключение статьи Комптона 1923 года он сообщил о результатах экспериментов, подтверждающих предсказания его формулы рассеяния, тем самым подтверждая предположение, что фотоны несут импульс, а также энергию в виде квантов. В начале своего вывода он постулировал выражение для импульса фотона, приравнивая уже установленное Эйнштейном соотношение массы и энергии E=mc^{2} квантованным энергиям фотонов {displaystyle hf,} которое Эйнштейн постулировал отдельно. Если {displaystyle mc^{2}=hf,} то эквивалентная масса фотона должна быть {displaystyle hf/c^{2}.} Тогда импульс фотона равен этой эффективной массе, умноженной на инвариантную скорость c фотона. Для фотона его импульс {displaystyle p=hf/c,} и, таким образом, {displaystyle hf} можно заменить на {displaystyle pc} для всех слагаемых содержащих импульс фотона, которые возникают в процессе вывода, приведённого ниже. Вывод, который появляется в статье Комптона, более краток, но следует той же логике в той же последовательности, что и приведённый вывод.

Закон сохранения энергии E просто уравнивает сумму энергий до и после рассеяния:

{displaystyle E_{gamma }+E_{e}=E_{gamma '}+E_{e'}~.!}

Комптон постулировал, что фотоны несут импульс[9] и таким образом, из закона сохранения импульса, импульсы частиц должны быть аналогичным образом связаны соотношением:

{displaystyle mathbf {p} _{gamma }=mathbf {p} _{gamma '}+mathbf {p} _{e'}~,}

в котором первоначальный импульс электрона {displaystyle {p_{e}}} опускается в предположении, что он фактически равен нулю.

Энергии фотонов связаны с частотами соотношениями:

{displaystyle E_{gamma }=hf!}
{displaystyle E_{gamma '}=hf'!~,}
где h — постоянная Планка.

Перед событием рассеяния электрон рассматривается как достаточно близкий к состоянию покоя, так что его полная энергия полностью состоит из его массы покоя, исходя из его энергии для {displaystyle m_{e}} получается:

{displaystyle E_{e}=m_{e}c^{2}~.!}

После рассеяния существует возможность того, что электрон может быть ускорен до значительной доли от скорости света, что означает, что его полная энергия должна быть представлена с использованием релятивистского соотношения энергия-импульса в виде:

{displaystyle E_{e'}={sqrt {(p_{e'}c)^{2}+(m_{e}c^{2})^{2}}}~.}

После подстановки этих величин в выражение для сохранения энергии получается:

{displaystyle hf+m_{e}c^{2}=hf'+{sqrt {(p_{e'}c)^{2}+(m_{e}c^{2})^{2}}}~.}

Это выражение можно использовать, чтобы найти величину импульса рассеянного электрона:

{displaystyle p_{e'}^{,2}c^{2}=(hf-hf'+m_{e}c^{2})^{2}-m_{e}^{2}c^{4}~.qquad qquad (1)!}

Эта величина импульса, полученного электроном (ранее равная нулю), превышает отношение энергию/c, потерянную фотоном:

{displaystyle {frac {1}{c}}{sqrt {(hf-hf'+m_{e}c^{2})^{2}-m_{e}^{2}c^{4}}}>{frac {hf-hf'}{c}}~.}

Уравнение (1) связывает различные энергии, рассмотренные при столкновении. Изменение импульса электрона включает релятивистское изменение энергии электрона, поэтому оно не связано просто с изменением энергии, происходящим в классической физике. Изменение величины импульса фотона связано не только с изменением его энергии, оно также предполагает изменение направления.

Решение уравнения для сохранения импульса относительно импульса рассеянного электрона приводит к:

{displaystyle mathbf {p} _{e'}=mathbf {p} _{gamma }-mathbf {p} _{gamma '}~.}

Использование скалярного произведения даёт квадрат его величины:

{displaystyle {begin{aligned}p_{e'}^{,2}&=mathbf {p} _{e'}cdot mathbf {p} _{e'}=(mathbf {p} _{gamma }-mathbf {p} _{gamma '})cdot (mathbf {p} _{gamma }-mathbf {p} _{gamma '})\&=p_{gamma }^{,2}+p_{gamma '}^{,2}-2p_{gamma },p_{gamma '}cos theta ~.end{aligned}}}

{displaystyle p_{gamma }c} заменяется {displaystyle hf,} и, умножая обе части на {displaystyle c^{2},} получается[13]:

{displaystyle p_{e'}^{,2}c^{2}=p_{gamma }^{,2}c^{2}+p_{gamma '}^{,2}c^{2}-2c^{2}p_{gamma },p_{gamma '}cos theta ~.}

После замены слагаемых с импульсом фотона на {displaystyle hf/c}, получается второе выражение для величины импульса рассеянного электрона:

{displaystyle p_{e'}^{,2}c^{2}=(hf)^{2}+(hf')^{2}-2(hf)(hf')cos {theta }~.qquad qquad (2)}

Приравнивая альтернативные выражения для этого импульса, получается выражение:

{displaystyle (hf-hf'+m_{e}c^{2})^{2}-m_{e}^{,2}c^{4}=left(hfright)^{2}+left(hf'right)^{2}-2h^{2}ff'cos {theta }~,}

которое после раскрытия квадрата и перестановки членов преобразуется к виду:

{displaystyle 2hfm_{e}c^{2}-2hf'm_{e}c^{2}=2h^{2}ff'left(1-cos theta right)~.}

Разделив обе стороны на {displaystyle 2hff'm_{e}c} получается:

{displaystyle {frac {c}{f'}}-{frac {c}{f}}={frac {h}{m_{e}c}}left(1-cos theta right)~.}

Наконец, поскольку {displaystyle flambda =f'lambda '=c}, то:

{displaystyle lambda '-lambda ={frac {h}{m_{e}c}}(1-cos {theta })~.qquad qquad (3)}

Кроме того, угол varphi между направлением отлетающего электрона и направлением падающего фотона определяется выражением:

{displaystyle cot varphi =left(1+{frac {hf}{m_{e}c^{2}}}right)tan(theta /2)~.qquad qquad (4)}

Сечение эффекта Комптона описывается формулой Клейна — Нишины.

Рассеяние на связанном электроне[править | править код]

Рис. 4. Схематическое изображение рассеяния фотона на электроне внешней оболочки атома

В случае, если электрон, на котором рассеивается фотон, находится в атоме, то картина рассеяния усложняется.

В случае, если энергия связи электрона больше энергии налетающего фотона, то электрон не выбивается из оболочки, и фотон рассеивается всем атомом как одним целым. В таком случае вместо массы электрона в формуле для изменения длины волны будет стоять масса атома, которая в десятки тысяч раз больше — а значит, и изменение длины волны будет в десятки тысяч раз меньше. Поэтому низкоэнергетические фотоны (например, видимого диапазона) рассеиваются почти упруго — такое рассеяние называется рэлеевским.

Другим возможным вариантом является рамановское рассеяние, при котором часть энергии фотона переходит в энергию собственных колебаний молекулы или наоборот.

В случае собственно комптоновского рассеяния, если энергия налетающего фотона значительно больше {displaystyle {mathcal {E}}_{0}gg alpha Z_{eff}m_{e}c^{2},} где alpha  — постоянная тонкой структуры, а {displaystyle Z_{eff}} — эффективный заряд ядра в единицах e (разный для разных оболочек), можно считать, что электрон свободен, и его рассеяние описывается формулами рассеяния на свободном электроне[14].

В случае, если {displaystyle m_{e}c^{2}gg {mathcal {E}}_{0}gg E_{3},} следует учесть, что в уравнение сохранения энергии при рассеянии добавляется член, связанный с энергией связи, а с другой стороны, проявляется взаимодействие электрона и покинутого им иона. Для описания такого процесса используются фейнмановские диаграммы типа «чайка»[15].

Вероятность рассеяния близка к нулю при низких энергиях налетающего фотона, она постепенно возрастает при увеличении энергии, а затем спадает. Положение пика зависит от эффективного заряда ядра: чем он больше, тем большей энергии соответствует пик. Также, чем больше значение заряда ядра, тем меньше, в абсолютных величинах, пиковое сечение рассеяния[16].

В угловом распределении при росте заряда ядра подавляются вылеты с малым углом — то есть, наибольшую вероятность при рассеянии на K-электронах тяжёлых элементов имеет отражение на 180°, даже для высоких энергий[14].

Ещё одной особенностью рассеяния на электронах в атоме является уширение спектральной линии, соответствующей заданному углу рассеяния. То есть, если при рассеянии на свободном электроне, любому углу соответствует конкретное значение {displaystyle Delta lambda ,} то при рассеянии на атоме каждому углу соответствует целый диапазон таких значений. Это происходит потому, что в атоме электрон локализован, а следовательно имеет неопределенность в импульсе. Ширина линии пропорциональна энергии падающего фотона, и квадратному корню от энергии связи электрона[17].

Поскольку обычно у атома есть много электронов с разной энергией связи, то при одной и той же энергии падающего фотона для некоторых электронов рассеяние будет происходить по комптоновскому типу, а для других (энергия связи которых больше энергии фотона) — по рэлеевскому, в зависимости от того, с электроном какой оболочки провзаимодействовал фотон. Поэтому реальные спектры рассеянных фотонов обычно содержат два пика — один из них совпадает с частотой падающего света, а второй — с менее энергетическими комптоновскими фотонами[18].

Комптоновское рассеяние на связанном электроне является основным способом потери энергии в веществе для гамма-квантов среднего диапазона энергий от 100 кэВ (1 МэВ для тяжёлых атомов) до нескольких МэВ. Для фотонов меньшей энергии важнее процессы рэлеевского рассеяния и фотоэффекта, а для более высокоэнергетических — процессы рождения электрон-позитронных пар в кулоновском поле ядра[19].

Некоторые особые случаи комптоновского рассеяния[править | править код]

Двойное рассеяние[править | править код]

Иногда в процессе рассеяния электрон может поглотить один фотон, а испустить два. Такой процесс происходит значительно реже обычного рассеяния. Наиболее вероятным является случай, когда один из образовавшихся фотонов очень низкоэнергетический, и вероятность излучения двух фотонов с близкими энергиями — минимальная[20].

Также, возможно излучение трёх и более фотонов, однако оно подавляется с множителем (постоянной тонкой структуры) (1/137)n-1, где n — количество фотонов[14].

При излучении двух и более фотонов теряется прямая зависимость между углом отклонения и изменением длины волны, поэтому правильный учёт шума от двойного комптон-эффекта необходим для точного измерения нормального эффекта Комптона.

Нелинейное рассеяние[править | править код]

В случае, если интенсивность падающего света очень велика, электрон может поглотить несколько фотонов, и испустить один — такой процесс называется нелинейным комптоновским рассеянием. Его сечение, в отличие от обычного рассеяния, зависит от плотности фотонов в пучке[21]. Рассеяние по такому каналу становится вероятным, когда напряжённость поля, создаваемого электромагнитной волной, превышает напряжённость поля в атоме (которая даже для водорода имеет величину около 4·1010 В/м[22]) более чем в 137 раз. Такие условия возникают при очень высокой интенсивности излучения и на 2020 год являются достижимыми лишь с помощью нескольких самых мощных в мире лазеров[23] (интенсивность излучения которых должна быть выше чем 1021 Вт/см[24]). В природе такие процессы могут реализовываться на поверхности нейтронных звёзд[15].

Рассеяния на тяжёлых частицах[править | править код]

Фотоны могут рассеиваться на протонах и нейтронах так же как на электронах, однако из-за того, что нуклоны почти в 2000 раз тяжелее электрона, изменение длины волны также в тысячи раз меньше, а потому заметным становится лишь для очень высокоэнергетических фотонов[15]. Кроме того, взаимодействие нуклонов в ядре значительно сложнее взаимодействия электрона с ядром, что также влияет на форму спектра рассеянных фотонов[25].

Применение[править | править код]

Измеряя интенсивность рассеянного света можно с большой точностью определить электронную плотность в теле[26].

Если объект имеет сложное внутреннее строение, то можно разделить рассеянное излучение, идущее от каждого отдельного участка вдоль луча. Таким образом работает комптоновская томография[27]. Её главным преимуществом является возможность просканировать объект, даже если отсутствует полный доступ к нему (невозможно произвести полный оборот излучателя и детектора), а недостатком — низкое разрешение.

Анализируя сечение комптоновского рассеяния при различных энергиях, можно установить распределение моментов движения электронов в различных оболочках. Зависимость сечения от энергии называется комптоновским профилем вещества[28]. Также знание комптоновского профиля нужно для высокоточной рентгенографии, поскольку комптоновское рассеяние зашумляет картину рентгеновской тени.

Использование эффекта Комптона позволяет создавать лазеры с плавной регулировкой длины волны — такая регулировка происходит вследствие вращения мишени вокруг рассеивателя[29].

Если фотон детектируется сначала одним детектором, а затем — другим, то, анализируя изменение энергии фотона, можно определить его начальную траекторию[30]. Так работают комптоновские гамма-телескопы[en], имеющие очень широкое поле зрения. Например, телескоп на орбитальной обсерватории «Комптон» имеет поле зрения в 1 стерадиан.

Обратное комптоновское рассеяния релятивистских электронов на реликтовом микроволновом излучении создаёт фотоны отдачи с энергией 50-100 кэВ[14]. Это явление известно как эффект Сюняева — Зельдовича. Детектируя такие высокоэнергетические фотоны, можно изучать крупномасштабное распределение материи во Вселенной. Самый полный обзор источников такого излучения был сделан космическим телескопом «Планк»[31].

Комптоновское рассеяние[править | править код]

Комптоновское рассеяние имеет первостепенное значение для радиобиологии, поскольку это наиболее вероятное взаимодействие гамма-лучей и рентгеновских лучей высоких энергий с атомами в живых организмах — применяется в лучевой терапии[32].

В материаловедении комптоновское рассеяние можно использовать для исследования волновой функции электронов в веществе в импульсном представлении[33].

Комптоновское рассеяние — важный эффект в гамма-спектроскопии, который приводит к возникновению комптоновского края, поскольку гамма-лучи также рассеиваются за пределы используемых детекторов. Комптоновское подавление используется для обнаружения паразитного рассеяния гамма-лучей, для учёта этого эффекта.

Магнитное комптоновское рассеяние[править | править код]

Магнитное комптоновское рассеяние — это модификация ранее упомянутой техники, которая включает намагничивание кристаллического образца, под действием высокоэнергетических циркулярно-поляризованных фотонов. Путём измерения энергии рассеянных фотонов и изменения намагниченности образца генерируются два разных комптоновских профиля (один для импульсов со спином вверх и один для импульсов со спином вниз). Разница между этими двумя профилями даёт магнитный профиль Комптона (МПК), определяемый функцией {displaystyle J_{text{mag}}(mathbf {p} _{z})} — одномерной проекцией спиновой плотности электронов.

{displaystyle J_{text{mag}}(mathbf {p} _{z})={frac {1}{mu }}iint _{-infty }^{infty }(n_{uparrow }(mathbf {p} )-n_{downarrow }(mathbf {p} ))dmathbf {p} _{x}dmathbf {p} _{y}~,}
где mu  — количество неспаренных электронов в системе;
{displaystyle n_{uparrow }(mathbf {p} )} и {displaystyle n_{downarrow }(mathbf {p} )} представляют собой трёхмерные распределения электронов по импульсам для электронов с основным и неосновным проекциями спина, соответственно.

Поскольку этот процесс рассеяния некогерентен (нет фазового соотношения между рассеянными фотонами), МПК представляет объёмные свойства образца и измеряет основное состояние. Это означает, что МПК идеален для сравнения с теоретическими методами, такими как теория функционала плотности. Площадь под графиком МПК прямо пропорциональна спиновому моменту системы, поэтому в сочетании с методами измерения полного магнитного момента (такими как СКВИД-магнитометрия) может использоваться для выделения как спинового, так и орбитального вкладов в общий магнитный момент системы. Форма МПК также даёт представление о происхождении магнетизма в системе[34].

Обратный комптоновский эффект[править | править код]

Если фотон рассеивается на движущихся электронах, то энергия рассеянного фотона может быть больше, чем энергия падающего (соответственно, энергия электрона после столкновения уменьшается). Такой процесс называют обратным комптоновским рассеянием. Этот процесс является основным механизмом потери энергии релятивистскими электронами в межзвёздном пространстве. Если начальные скорости фотонов распределены изотропно, то средняя энергия рассеянных фотонов будет равняться[35]:

{displaystyle {mathcal {E}}_{1}={mathcal {E}}_{0}{frac {4E_{e}}{3m_{e}c^{2}}}~,}

Энергия рассеянного на электроне фотона:

{displaystyle {mathcal {E}}_{1}={mathcal {E}}_{0}{frac {1-beta cos theta }{1-beta cos(theta -phi )+{frac {{mathcal {E}}_{0}}{E_{e0}}}(1-cos phi )}}~,}
где: theta  — угол между направлениями их движения;
phi  — угол между направлениями движения падающего и рассеянного фотона;
{displaystyle beta =v/c}[35] — безразмерная скорость электрона.

В случае «лобового» столкновения[35]:

{displaystyle {mathcal {E}}_{1}=E_{e0}{frac {4{mathcal {E}}_{0}E_{e0}}{4{mathcal {E}}_{0}E_{e0}+m^{2}c^{4}}}~.}

В случае обратного эффекта Комптона изменение длины волны падающего света зависит от его начальной энергии, тогда как для неподвижных электронов такой зависимости нет.

Обратный эффект Комптона ответственен за рентгеновское излучение галактических источников, рентгеновскую составляющую реликтового фонового излучения (эффект Сюняева — Зельдовича), трансформацию плазменных волн в высокочастотные электромагнитные волны[36]. Эффект также наблюдается, когда фотоны космического микроволнового фона движутся через горячий газ, окружающий скопление галактик. Фотоны реликтового излучения рассеиваются электронами в этом газе до более высоких энергий, что приводит к эффекту Сюняева — Зельдовича. Наблюдения этого эффекта обеспечивают практически независимые от красного смещения средства обнаружения скоплений галактик.

Обратное комптоновское рассеяние играет важную роль в астрофизике. В рентгеновской астрономии предполагается, что аккреционный диск, окружающий черную дыру, создаёт тепловой спектр. Фотоны с более низкой энергией из этого спектра, рассеиваются до более высоких энергий релятивистскими электронами в окружающей короне. Предполагается, что это вызывает степенну́ю составляющую в рентгеновских спектрах (0,2-10 кэВ) аккреции черных дыр[источник не указан 760 дней].

Некоторые установки синхротронного излучения рассеивают лазерный свет от ускорительного электронного луча. Это комптоновское обратное рассеяние производит фотоны высоких энергий в диапазоне от МэВ до ГэВ[37][38] и впоследствии используются в экспериментах по ядерной физике.

Примечания[править | править код]

  1. ↑ Комптон А. Рассеяние рентгеновских лучей как частиц // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 398—404. — 2600 экз.
  2. ↑ Филонович С. Р. Артур Комптон и его открытие // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 405—422. — 2600 экз.
  3. ↑ Prof. Jeffrey Coderre. Interactions of Photons with Matter. ocw.mit.edu (2004).
  4. ↑ Юдин Г. Л. Комптона эффект // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.: «Комптон рассмотрел упругое рассеяние фотона на свободном покоящемся электроне».
  5. ↑ Биленький С. М. Рассеяние микрочастиц // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.: «Рассеяние микрочастиц — процесс столкновения частиц, в результате которого либо меняются их импульсы (упругое рассеяние) или наряду с изменением импульсов меняются также внутр[енние] состояния частиц, либо образуются др[угие] частицы (неупругие процессы)».
  6. ↑ Christillin P. (1986). “Nuclear Compton scattering”. J. Phys. G: Nucl. Phys. 12 (9): 837—851. Bibcode:1986JPhG…12..837C. DOI:10.1088/0305-4616/12/9/008.
  7. ↑ Griffiths, David. Introduction to Elementary Particles. — Wiley, 1987. — P. 15, 91. — ISBN 0-471-60386-4.
  8. ↑ C. Moore. Observation of the Transition from Thomson to Compton Scattering in Optical Multiphoton Interactions with Electrons.
  9. ↑ 1 2 3 Taylor, J.R. Modern Physics for Scientists and Engineers / J.R. Taylor, C.D. Zafiratos, M.A. Dubson. — 2nd. — Prentice Hall, 2004. — P. 136–9. — ISBN 0-13-805715-X.
  10. ↑ Сивухин, 1986, p. 31.
  11. ↑ Сивухин, 1986, p. 32.
  12. ↑ Сивухин, 1986, p. 30.
  13. ↑ Борн М. Атомная физика. — М.: Мир, 1965. — С. 389.
  14. ↑ 1 2 3 4 Прохоров, 1990, p. 431.
  15. ↑ 1 2 3 Прохоров, 1990, p. 432.
  16. ↑ Mikhailov Aleksandr, …, Nefiodov Andrei (2018). “Ionization-Excitation of Helium-Like Ions at Compton Scattering”. Journal of Experimental and Theoretical Physics. 127: 620—626. DOI:10.1134/S1063776118090170. Дата обращения 26 липня 2020.
  17. ↑ Kaplan Ilya, …, Yudin Gennadiy (1975). “Nonrelativistic compton effect for a bound electron” (PDF). Journal of Experimental and Theoretical Physics. 69 (1): 9—22. Дата обращения 26 липня 2020.
  18. ↑ R. Nave. Compton Scattering Data. HyperPhysics. Дата обращения: 26 липня 2020. Архивировано 23 лютого 2010 года.
  19. ↑ Ишханов,Капитонов,Кэбин, 2007, p. 535.
  20. ↑ Mandl Franz et. al. (1952). “The theory of the double Compton effect”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 215 (1123): 497—507. DOI:10.1098/rspa.1952.0227.
  21. ↑ Ivanov Dmitry et. al. (2006). “Complete Description of Non-Linear Compton and Breit-Wheeler Processes”. Acta Physica Polonica B. 37 (4): 1073.
  22. ↑ Dr. Susan Lea. Electric fields in dielectrics. San Francisco State University (2006).
  23. ↑ Danson; et al. (2019). “Petawatt and exawatt class lasers worldwide” (PDF). High Power Laser Science and Engineering. 7: 54. DOI:10.1017/hpl.2019.36.
  24. ↑ Bisesto; et al. (2018). “Evolution of the electric fields induced in high intensity laser–matter interactions”. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 909: 398—401. DOI:10.1016/j.nima.2018.03.040.
  25. ↑ Bernardini et. al. (1960). “Proton compton effect”. Il Nuovo Cimento (1955-1965). 18: 1203—1236. DOI:10.1007/BF02733177. Дата обращения 31 липня 2020.
  26. ↑ Sharaf, Jamal (2001). “Practical aspects of Compton scatter densitometry”. Applied Radiation and Isotopes. 54 (5): 801—809. DOI:10.1016/S0969-8043(00)00333-X. Дата обращения 26 липня 2020.
  27. ↑ Redler (2018). “Compton scatter imaging: A promising modality for image guidance in lung stereotactic body radiation therapy”. Medical Physics. 45 (3): 1233—1240. DOI:10.1002/mp.12755. Дата обращения 26 липня 2020.
  28. ↑ Rao; et al. (2002). “Doppler Broadening and its Contribution to Compton Energy-Absorption Cross Sections: An Analysis of the Compton Component in Terms of Mass-Energy Absorption Coefficient” (PDF). Journal of Physical and Chemical Reference Data. 31 (3): 769. DOI:10.1063/1.1481880. Дата обращения 26 липня 2020.
  29. ↑ Источники гамма-излучения. Ядерная физика в Интернете. Дата обращения: 26 липня 2020. Архивировано 21 березня 2021 года.
  30. ↑ The Imaging Compton Telescope (COMPTEL). Nasa.gov (2005). Дата обращения: 27 липня 2020. Архивировано 21 березня 2021 года.
  31. ↑ Planck Collaboration (2014). “Planck 2013 results. XXIX. The Planck catalogue of Sunyaev-Zeldovich sources” (PDF). Astronomy & Astrophysics. 571: 41. DOI:10.1051/0004-6361/201321523. Дата обращения 7 березня 2021.
  32. ↑ Camphausen KA, Lawrence RC. «Principles of Radiation Therapy» in Pazdur R, Wagman LD, Camphausen KA, Hoskins WJ (Eds) Cancer Management: A Multidisciplinary Approach. 11 ed. 2008.
  33. ↑ I. G. Kaplan (2003). “Compton scattering beyond the impulse approximation”. Physical Review B. 68: 235104. arXiv:cond-mat/0304294. DOI:10.1103/PhysRevB.68.235104.
  34. ↑ Malcolm Cooper. X-Ray Compton Scattering. — OUP Oxford, 14 October 2004. — ISBN 978-0-19-850168-8.
  35. ↑ 1 2 3 Эффект Комптона. Ядерная физика в Интернете. Дата обращения: 25 липня 2020. Архивировано 21 березня 2021 года.
  36. ↑ Комптона эффект // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
  37. ↑ GRAAL home page. Lnf.infn.it. Дата обращения: 8 ноября 2011.
  38. ↑ Duke University TUNL HIGS Facility. Дата обращения: 31 января 2021.

Литература[править | править код]

  • Сивухин Д. В. Атомная физика // Общий курс физики. — М.: Наука, 1986. — Т. 5. — 426 с.
  • Комптона эффект // Физическая энциклопедия / А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 703 с.
  • Ишханов Б. С., Капитонов И. М., Кэбин Э. И. Частицы и атомные ядра: Основные понятия. — М.: ЛКИ, 2007. — 584 с.
Источник

Макеты страниц

Воспользовавшись соотношением (4.2.6), определяющим как функцию , можно выразить дифференциальное сечение рассеяния неполяризованных фотонов покоящимися неполяризованными электронами через частоту падающего фотона и угол рассеяния фотона:

Угловое распределение, даваемое этой формулой, изображено на рис. 4.2 для различных значений параметра

При малых энергиях фотона () формула (4.2.18) переходит в классическую формулу Томсона

    (4.2.19)

Если энергия первичного фотона велика по сравнению с энергией покоя электрона, , то из (4.2.18) можно получить простые выражения для двух предельных случаев: когда и когда

В предельном случае больших энергий угловое распределение имеет особенно простой вид в с. ц. и. сталкивающихся частиц:

В области углов, не близких к 180°, дифференциальное сечение существенно меньше:

Дифференциальное сечение рассеяния покоящимся электроном может быть выражено с помощью (4.2.6) через энергию рассеянного фотона. После интегрирования по азимутальному углу получим

где согласно (4.2.6), изменяется в пределах

Для получения полного сечения нужно проинтегрировать (4.2.18) по углу Ф:

    (4.2.21)

где Заметим, что сечение является релятивистским инвариантом, поэтому у также можно выразить через инвариантную величину согласно (4.2.9)

При разложение (4.2.21) по у дает

    (4.2.22)

т. е. в нерелятивистской области сечение рассеяния почти не зависит от энергии фотона. В крайне релятивистской области выражение для сечения сильно упрощается:

В этой области сечение убывает почти обратно пропорционально энергии фотона.

Таким образом, в области больших энергий число рассеянных фотонов сильно уменьшается, благодаря чему проникающая способность у-излучения возрастает с увеличением их энергии.

Рис. 4.3.

На рис. 4.3 представлена зависимость сечения от энергии первичного фотона.

В результате столкновения с фотоном покоящийся вначале электрон приобретает энергию

    (4.2.23)

Угол между импульсом рассеянного электрона и импульсом первичного фотона связан с углом соотношением

Воспользовавшись этим соотношением, можно выразить через . Мы получим, таким образом, угловое распределений электронов отдачи

    (4.2.25)

где — элемент телесного угла, в котором лежит импульс рассеянного электрона.

В крайне релятивистском случае эта формула дает

Источник

Современная физика описывает явления, которые, на первый взгляд, противоречат здравому смыслу. Знаете ли вы, что свет может взаимодействовать с электронами? В результате этих взаимодействий электрон может достичь определенной скорости, а свет… меняет свое направление и длину волны. Это явление называется эффектом Комптона. Проанализировав эту статью, вы увидите, что этот удивительный эффект имеет очень простое объяснение. Чтобы понять его, нам понадобятся лишь базовые знания механики и простые факты из современной физики.

Простое объяснение эффекта Комптона

Эффект Комптона — это явление, при котором свет взаимодействует с электронами. Давайте сначала уточним, что именно мы подразумеваем под словом «свет». Оказалось, что свет имеет двойственную природу — в одних экспериментах его природа волновая, в других — корпускулярная.

Свет как волны или как частицы

Рис. 1. Следует ли рассматривать свет как волны или как частицы?

Свет волновой природы — это электромагнитные волны (или электромагнитное излучение), с которыми мы знакомы. Подтверждение того, что свет может вести себя как волна, было получено в 1803 году английским физиком Томасом Янгом. Он провел серию гениальных экспериментов, в которых показал, что свет претерпевает дифракцию и интерференцию, то есть явления, характерные для волн. Эти эксперименты XIX века утвердили мнение о том, что свет является разновидностью волны.

Это мнение оставалось практически неизменным в течение 100 лет! Однако уже в то время были обнаружены явления и эффекты, которые нельзя было объяснить, исходя из того, что свет имеет только волновую природу. Фотоэлектрический эффект, заключающийся в выбросе электронов с поверхности металлов, оказался большой проблемой. Свойства этого явления противоречили волновой природе света.

В 1900 году немецким физиком Максом Планком была написана первая статья, постулирующая частичную природу света. В 1905 году на основе работы Планка световая квантовая гипотеза была представлена Альбертом Эйнштейном, также уроженцем Германской империи того времени. Эта гипотеза постулировала, что свет можно рассматривать как поток частиц. Наименьшая «порция» света (квант света) называется фотоном. Используя свою гипотезу, Эйнштейн смог объяснить фотоэлектрический эффект и его свойства. В 1921 году за это объяснение он получил Нобелевскую премию.

Давайте теперь вернемся к эффекту Комптона. Он получил свое название от имени американского физика Артура Холли Комптона. Комптон изучал рассеяние рентгеновских лучей. Полученные им результаты не соответствовали волновой природе света в то время. Для того чтобы правильно объяснить полученные результаты, Комптон, как и Эйнштейн, должен был предположить, что свет состоит из потока частиц. В 1923 году физик опубликовал работу, описывающую новый эффект, и очень скоро, в 1927 году, он получил Нобелевскую премию за свои исследования! Как видите, в то время новая, зарождающаяся отрасль физики (сейчас она называется современной физикой) была полем многих захватывающих и новаторских научных исследований.

Эффект Комптона делает известной как волновую, так и корпускулярную природу света. Этот эффект связан с взаимодействием рентгеновских и гамма-лучей с электронами. В результате этого взаимодействия электрон приобретает определенную скорость и выбрасывается, а излучение меняет направление и длину волны. Когда излучение, особенно свет, меняет направление, мы говорим, что оно рассеяно. Схема явления Комптона показана на рис. 2.

Схема Комптона

Рис. 2. Схема эффекта Комптона

В явлении Комптона излучение с длиной волны λf падает на свободный или слабо связанный электрон. Что это значит? «Свободный» электрон не взаимодействует ни с какими другими объектами, в то время как «слабо связанным» электрон называется тогда, когда энергия связи электрона намного меньше энергии падающего фотона.

В результате освещения электрон приобретает определенную скорость под углом φ к первоначальному направлению распространения излучения. Излучение, в свою очередь, рассеивается под углом θ к первоначальному направлению, длина волны также изменяется, и ее новое значение составляет λf‘.

Формулы для расчета энергии и импульса фотона

Чтобы понять и описать, что происходит во время эффекта Комптона, давайте рассматривать рентгеновские лучи (или гамма-лучи) как поток частиц. Если бы мы использовали только волновое описание, изменение длины волны излучения не могло бы быть объяснено. Такой эффект не возникает при классическом рассеянии. Если предположить, что мы рассматриваем излучение как поток фотонов, то мы имеем дело с упругим столкновением одной частицы (фотона) с другой частицей (электроном). Упругое столкновение можно рассматривать на основе известных законов механики — должны выполняться принципы сохранения импульса и энергии:

Эффект Комптона формулы

где буквы p и E обозначают импульс и энергию частицы, соответственно. Подстрочные индексы f и e означают фотон и электрон, соответственно. «Штрихованные» индексы относится к величинам после рассеяния, «нештрихованные» индексы — к величинам до рассеяния. Итак, нам удалось свести сложный вопрос современной физики к простой механике, как при столкновении бильярдных шаров!

Для справки. Упругое столкновение — столкновение, при котором импульс и энергия системы (в классической физике — кинетическая энергия) не изменяются.

Чтобы решить приведенную выше систему уравнений и определить неизвестные значения импульса и энергии после рассеяния, необходимо разложить вектор импульса на составляющие. В нашем двумерном случае мы получаем в общей сложности три уравнения: два, описывающие импульс (в горизонтальном и вертикальном направлениях), и одно, описывающее энергию:

Уравнения эффект Комптона

Что такое импульс и энергия фотона? Для их определения мы должны обратиться к двойственной природе излучения. Значение импульса фотона (частицы) связано с длиной волны света λ следующим соотношением: pf = h / λ .

где h = 6,63 * 10-34 Дж*с — постоянная Планка. Энергия фотона составляет: Ef = pf * c = h*c / λ

где c = 3 * 108 м/с — скорость света в вакууме. Вы уже видите взаимосвязь природы волн и частиц? Чтобы объяснить явление Комптона, мы должны рассматривать излучение как поток частиц, которые, подобно пулям, сталкиваются с электронами и приводят их в движение. С другой стороны, мы не можем определить энергию и импульс фотонов, не обращаясь к их волновой природе.

Формулы для расчета импульса и энергии релятивистских частиц

А каковы будут импульс и энергия электрона? В явлении Комптона отражающийся электрон может достигать очень высоких скоростей, составляющих значительную долю скорости света. Это означает, что к электрону нужно относиться релятивистски. Нельзя записать импульс и энергию электрона классическим способом, потому что масса движущегося электрона отличается от его массы покоя (и зависит от скорости). Релятивистская связь между энергией E и импульсом p следующая:

E = m0 * c4 + p2 * c2

где m0 — масса покоя. Для электрона это m0 = 9,1*10-31 кг. Далее мы будем обозначать массу покоя электрона через me. Конечно, если мы используем релятивистское выражение для движущегося электрона, то это же выражение должно быть использовано «с другой стороны уравнения» для покоящегося электрона. Когда электрон находится в состоянии покоя (до освещения), его импульс равен нулю, что означает, что мы можем выразить энергию (покоя) как: Ee = me * c2 .

В релятивистской физике мы говорим, что энергия покоя связана только с тем, что тело наделено массой. В этом смысл знаменитой формулы Эйнштейна — энергия и масса эквивалентны. Увеличение энергии тела приводит к увеличению его массы.

Анализируя рис. 2, мы видим, что отдельные компоненты импульса могут быть определены простыми тригонометрическими соотношениями. Таким образом, в конечном итоге наша система уравнений принимает вид, показанный ниже. Первое уравнение относится к горизонтальной составляющей импульса, второе — к вертикальной, а третье выражает принцип сохранения энергии.

Система уравнений эффект комптона

В типичном лабораторном эксперименте мы освещаем электроны излучением с фиксированной длиной волны λ и получаем, как правило, угол рассеяния фотона θ. Тогда неизвестные в приведенной выше системе уравнений имеют вид λ‘, p‘e и φ. Для получения окончательного выражения, описывающего эффект Комптона, эта система обычно преобразуется к форме, показанной ниже. Мы рекомендуем вам провести эти расчеты самостоятельно. В Интернете вы найдете множество советов о том, как это сделать.

Δλ = λ‘ — λ = ( h / me * c ) * ( 1 — cos θ )

Эта форма решения позволяет нам быстро определить разность длин волн между падающим и рассеянным фотоном. Зная длину волны падающего фотона и угол рассеяния фотона θ , мы можем быстро определить длину волны рассеянного фотона. Зная длины волн, мы можем вычислить энергии обоих фотонов, а затем, исходя из принципа сохранения энергии, энергию электрона после рассеяния.

Разница Δλ = λ‘ — λ называется комптоновским сдвигом или комптоновским смещением. Выражение λc = h / me * c ≈ 2,43 * 10-12 м называется комптоновской длиной волны.

Если выражаться образно, то можно сказать, что излучение после столкновения со свободными электронами меняет направление… и цвет — потому что меняется длина волны. Однако такое утверждение не совсем точно. Когда мы говорим о «цвете света», мы имеем в виду свет видимого диапазона, то есть с длиной волны от 400 до 700 нм. Комптоновское рассеяние, однако, не наблюдается для видимого излучения. Эффект возникает для рентгеновских и гамма-лучей, т.е. для излучения с на порядки большей энергией фотонов (или на много порядков меньшей длиной волны), чем видимый свет.

Два случая комптоновского рассеяния

Рассмотрим теперь два крайних случая комптоновского рассеяния. Первый возникает, когда угол рассеяния фотона θ = 0°. Это означает, что фотон не меняет своего направления после столкновения с электроном. Эта ситуация показана на рис. 3. Мы видим, что:

λ‘ — λ = ( h / me * c ) * (1 — 1) = 0 → λ‘ = λ

Длина волны фотона до и после столкновения одинакова. Это означает, что фотон не передает импульс или энергию электрону. Поэтому электрон остается в состоянии покоя, а фотон продолжает двигаться без рассеяния.

Случай отсутствия рассеяния в явлении Комптона

Рис. 3. Случай «отсутствия» рассеяния в явлении Комптона

Другой крайний случай — когда θ = 180°. Образно говоря, фотон «отскакивает» от электрона и начинает двигаться в прямо противоположном направлении. Такая ситуация называется обратным рассеянием фотона. Тогда у нас есть:

λ = ( h / me * c ) * (1 + 1) = 2h / me * c

При обратном рассеянии разность длин волн фотона принимает максимально возможное значение. Это означает, что фотон передает электрону максимально возможную энергию и импульс. Эта ситуация показана на рис. 4.

Случай обратного рассеяния в явлении Комптона

Рис. 4. Случай обратного рассеяния в явлении Комптона

Список использованной литературы

  1. Комптон А. Рассеяние рентгеновских лучей как частиц // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 398—404. — 2600 экз.
  2. Camphausen KA, Lawrence RC. «Principles of Radiation Therapy» in Pazdur R, Wagman LD, Camphausen KA, Hoskins WJ (Eds) Cancer Management: A Multidisciplinary Approach. 11 ed. 2008.
  3. Филонович С. Р. Артур Комптон и его открытие // Эйнштейновский сборник 1986—1990. — М.: Наука, 1990. — С. 405—422. — 2600 экз.
  4. Эффект Комптона. Учебно-методическое пособие / Р.Р. Гайнов, Е.Н. Дулов, М.М. Бикчантаев // Казань: Казанский (Приволжский) федеральный университет, 2013. – 24 с.: 7 илл.
Источник

В сегодняшней статье решаем задачи по физике. Тема – эффект Комптона.

Подпишитесь на наш телеграм, там много полезных материалов для учебы. А если хотите скидку, ищите ее на нашем втором канале для клиентов.

Нужна помощь?

Доверь свою работу кандидату наук!

Задачи на тему «эффект Комптона»

Не знаете, с чего начать решение? Вот вам общая памятка по решению физических задач и более 40 формул, держите их под рукой!

Кстати, у нас есть еще и справочник с теорией. Нужна теория по эффекту Комптона? Пожалуйста!

Задача на эффект Комптона №1

Условие

Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Найти угол комптоновского рассеяния, если длина волны излучения увеличилась на 1 пм.

Решение

Запишем формулу эффекта Комптона:

λ’-λ=2λсеsin2θ2

Отсюда найдем искомый угол θ:

θ=2acrsin∆λ2λec=2arcsin1·10-122·2,4263·10-12=53,95°

Ответ: θ=53,95°.

Задача на эффект Комптона №2

Условие

Гамма-излучение с длиной волны 0,83·10-13 м  рассеялось на свободных протонах под углом 180°. Найти энергию фотона после рассеяния.

Решение

По формуле эффекта Комптона:

λ’=λ+λpc·1-cosθ

Отсюда:

λ’=0,83·10-13+1,3214·10-15·1–1≈8,56·10-14 м

Выразим энергию через длину волны:

Е’=hcλ’=6,62·10-34·3·1088,56·10-14=2,32·10-12Дж

Ответ: 2,32 пДж

Задача на эффект Комптона №3

Условие

В результате комптоновского рассеяния под углом 174° длина волны фотона стала равной 8 пм. Во сколько раз уменьшилась частота фотона?

Решение

Из формулы для эффекта Комптона найдем:

λ’-λ=λес·1-cosθλ=λ’-λec·1-cosθλ=8·10-12-2,4263·10-121–0,9945≈3,16·10-12 м

Частоту фотона после рассеяния найдем из формулы для длины волны:

λ=сϑϑ=сλ=3·1083,16·10-12=94,87·1018 Гц

Частота фотона до рассеивания:

ϑ’=сλ’=3·1088·10-12=37,47·1018 Гц

Отсюда:

ϑϑ’=94,8737,47≈2,5

Ответ: уменьшилась в 2,5 раза.

Задача на эффект Комптона №4

Условие

В результате эффекта Комптона фотон с энергией  ε1=1,02 МэВ рассеян на свободных электронах на угол θ=150°. Определить энергию  рассеянного фотона.

Решение

Согласно формуле Комптона изменение длины волны фотона при рассеянии на свободном электроне:

∆λ=hcE01-cosθ

Здесь E0 – энергия покоя электрона.

С учетом того, что ε=hϑ=hcλ и λ=hcε, первую формулу можно переписать в следующем виде:

hcε-hcε1=hcε01-cosθ

Отсюда можно найти энергию рассеянного фотона ε2:

1ε2-1ε1=1-cosθE0ε2=ε1E0E0+ε11-cosθ

Энергия покоя электрона равна E0=mc2

Подставим значения и рассчитаем:

Е0=9,11·10-31·9·1016=8,199·10-14 Дж=0,511·106 эВ=0,511 МэВε2=1,02·0,5110,511+1,021-сos150°=0,216 МэВ

Ответ: 0,216 МэВ.

Задача на эффект Комптона №5

Условие

При каком угле рассеивания фотонов происходит максимально возможное изменение длины волны?

Решение

Длина волны рассеянного фотона в результате эффекта Комптона возрастает тем больше, чем больше угол рассеивания фотона. Максимально возможное значение этого угла θ=180°, т.е. фотон меняет направление движения на противоположное. Тогда формула Комптона принимает вид:

λ’-λ=2λс

Ответ: 180°.

Нужно больше задач? Не проблема! Вот, например, задачи на фотоэффект.

Вопросы на тему «эффект Комптона»

Вопрос 1. В чем суть эффекта Комптона?

Ответ. Эффект Комптона – явление, сопровождающее рассеяние электромагнитного излучения на свободных (слабосвязанных) электронах атома, приводящее к изменению его частоты (длины волны).

Вопрос 2. Какие закономерности существуют для комптоновского рассеяния?

Ответ. Комптоновское рассеяние подчиняется следующим закономерностям:

  • рассеянное излучение обладает высокой интенсивностью для веществ с малым атомным весом и малой интенсивностью для веществ с большим атомным весом;
  • при увеличении угла рассеяния интенсивность рассеянного излучения в эффекте Комптона возрастает (интенсивность при классическом рассеянии падает с увеличением угла рассеяния);
  • смещение длины волны рассеянного излучения зависит от угла рассеяния;
  • при одинаковых углах рассеяния величина смещения одна и та же для всех рассеивающих веществ.

Вопрос 3. Что такое комптоновская длина волны?

Ответ. Комптоновская длина волны является постоянной величиной для частицы, на которой происходит рассеяние электромагнитного излучения.

λс=hmc

Здесь m – масса частицы, на которой происходит рассеяние.

Вопрос 4. Запишите формулу Комптона.

Ответ. Формула комптона имеет вид:

∆λ=λ’-λ=λс1-cosθ

Здесь λ – длина волны падающего излучения, λ’– длина волны рассеянного излучения, θ – угол рассеяния, λс – комптоновская длина волны.

Вопрос 5. Какую премию получил Комптон за открытие данного эффекта?

Ответ. В 1927 году Комптон (совместно с Вильсоном) получил Нобелевскую премию.

Посмотри примеры работ и убедись, что мы поможем на совесть!

Нужна помощь в решении задач? В профессиональном сервисе для учащихся вам помогут решить любую, хоть с тремя звездочками. Обращайтесь в любое время.

Источник

Добавить комментарий