Развертка конуса. Построение развертки конуса.
Развертка конуса. Построение развертки конуса.
Оцените запись
Развертка конуса. Построение развертки конуса.
Поверхность конуса состоит из боковой поверхности и поверхности основания.
Расчет развертки конуса.
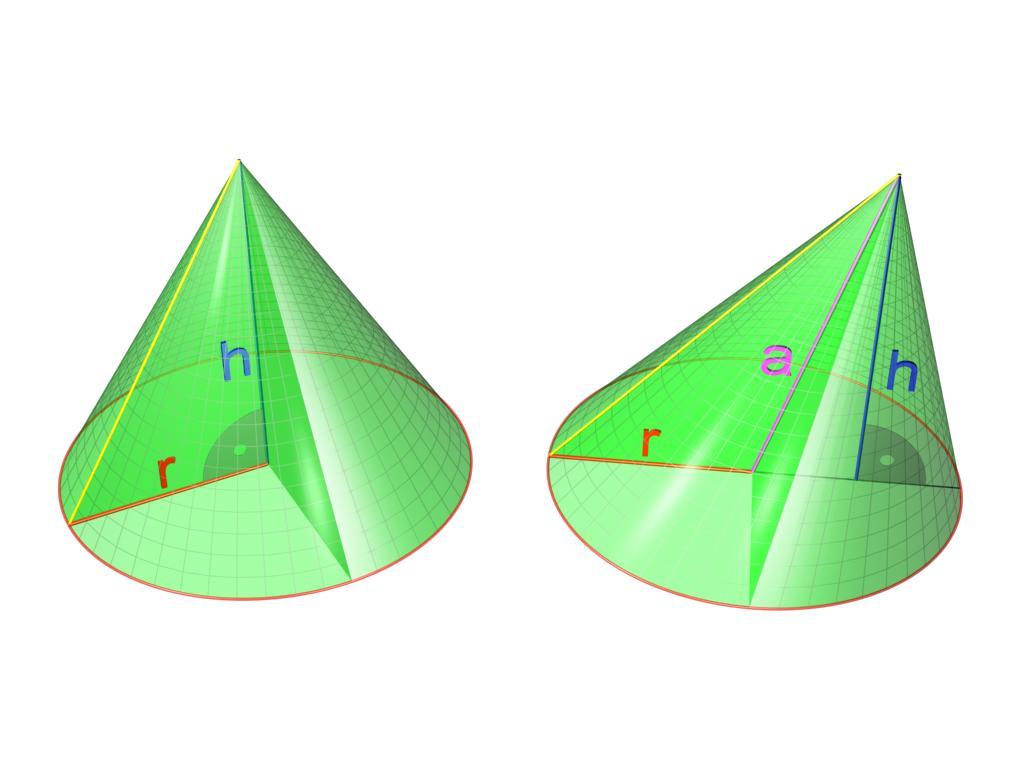
Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:
т. е. как гипотенуза прямоугольного треугольника.
Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.
Рис. 1. Развертка конуса:
а — проекция; б — развертка.
Угол развертки конуса.
Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ, равный длине окружности основания конуса 2 π r. Длине дуги в 2 π r соответствует угол α, величина которого определяется по формуле:
где
г — радиус окружности основания конуса;
l — длина образующей конуса.
Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углу α. Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.
Найденные точки КМ соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.
ЧИТАЙТЕ ТАКЖЕ:
Построение развертки конуса
Развертка поверхности конуса – это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
- Прямой круговой конус
- Наклонный конус
- Усеченный конус
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
Алгоритм построения
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
Пример
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Алгоритм
- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5. - Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Алгоритм
- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
- Соединяем точки A0, B0, C0 плавной линией.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Алгоритм
- Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
- Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
- Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
- Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.
Каждый школьник слышал о круглом конусе и представляет, как выглядит эта объемная фигура. В данной статье дается определение развертки конуса, приводятся формулы, описывающие ее характеристики, а также описывается способ ее построения с помощью циркуля, транспортира и линейки.
Круглый конус в геометрии
Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.
Круг называется основанием фигуры, его окружность – это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются – это вершина конуса.
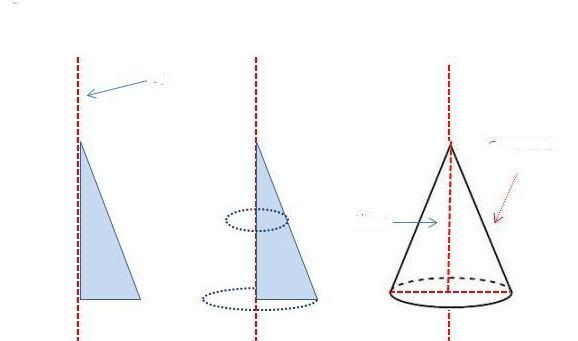
Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.
Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.
Получение фигуры с помощью вращения
Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.
Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c – это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.
Очевидно, что катет a будет радиусом основания фигуры, катет b – его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.
Вид развертки конуса
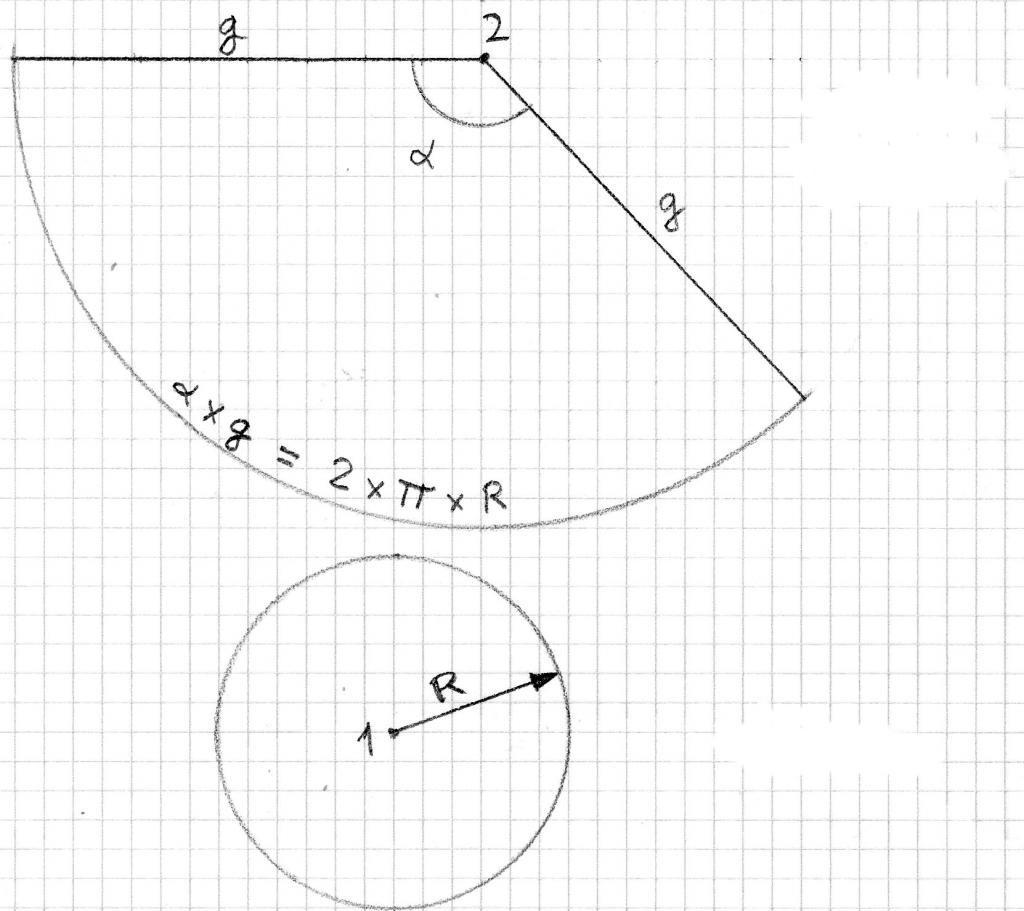
Как можно догадаться, конус образован двумя типами поверхностей. Одна из них – это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.
Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.
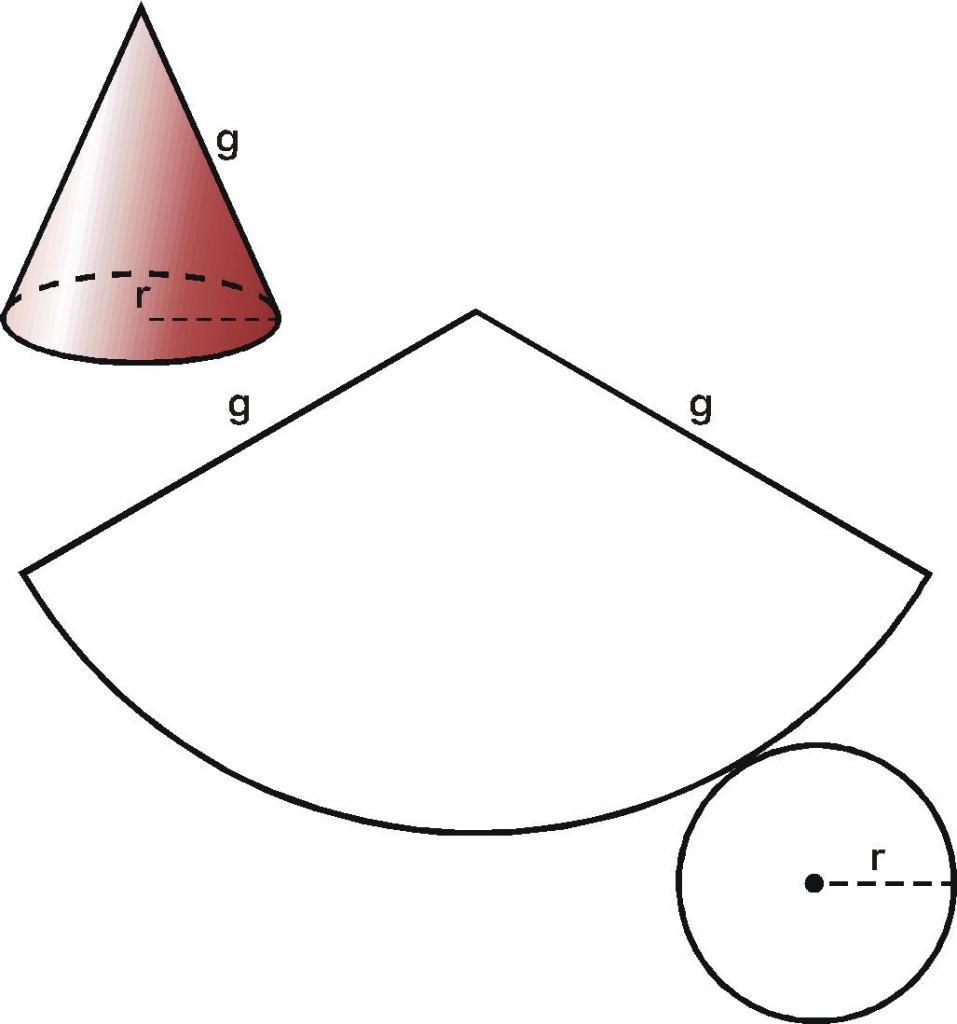
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.
Угол и площадь развертки
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.
Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:
l = 2*pi*r.
Если бы весь круг радиусом g был построен, то его бы длина составила:
L = 2*pi*g.
Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:
L ==> 2*pi;
l ==> φ.
Тогда неизвестный угол φ будет равен:
φ = 2*pi*l/L.
Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:
φ = 2*pi*r/g.
Угол φ здесь выражен в радианах.
Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:
2*pi ==> pi*g2;
φ ==> Sb.
Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:
Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.
Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.
Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:
S = Sb + So = pi*r*(g + r).
Построение развертки конуса на бумаге
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.
В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.
Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:
φ = 2*pi*r/g = 2*pi*3/5 = 216o.
Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.
Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.
Пример решения геометрической задачи
Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.
Задача не является сложной, если вспомнить, что круглый конус – это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:
g2 = h2 + r2.
Вторым выражением, которое следует использовать при решении, является формула для угла φ:
φ = 2*pi*r/g.
Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).
Выражаем из второй формулы g и подставляем результат в первую, получаем:
g = 2*pi*r/φ;
h2 + r2 = 4*pi2*r2/φ2 =>
r = h /√(4*pi2/φ2 – 1).
Угол φ = 120o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:
r = h /√8;
g =3*h /√8.
Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.
Выкройка для конуса

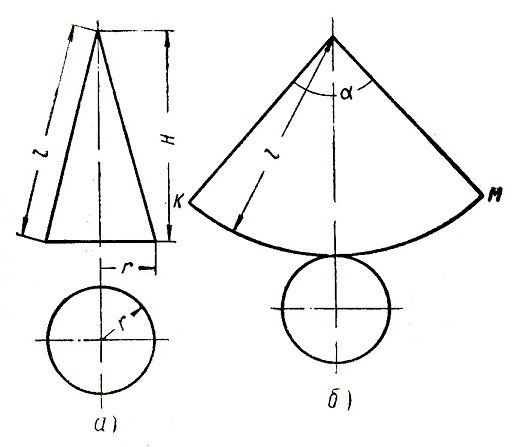
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Обозначения:
— диаметр основания конуса;
— высота конуса;
— радиус дуги выкройки;
— центральный угол выкройки.
Параметры выкройки рассчитываются по формулам:


где 
2. Усеченный конус
Обозначения:
— диаметр большего основания конуса;
— диаметр меньшего основания конуса;
— высота конуса;
— радиус внешней дуги выкройки;
— радиус внутренней дуги выкройки;
— центральный угол выкройки.
Формулы для вычисления параметров выкройки:



где 
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них 
3. Угол при вершине конуса
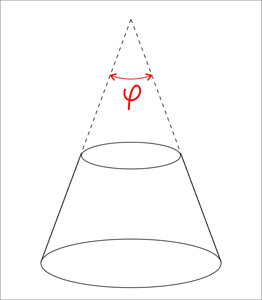

В этом случае мы можем его использовать вместо одного из трех входных значений: 


Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
4. Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Excel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.
§ 18. Конус
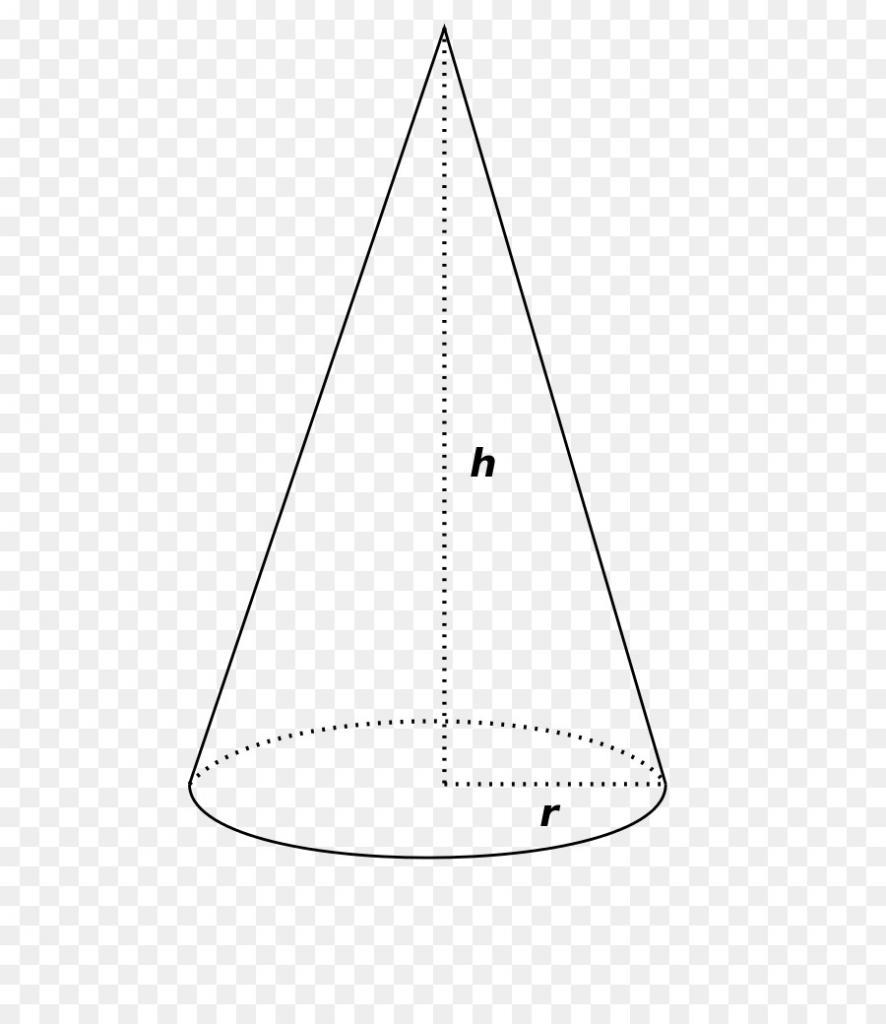
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.
Рис. 165
Рис. 166
Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение 


18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.
Рис. 168
Рис. 169
Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.
Рис. 171

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.
Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = 



Тогда S△ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.
Рис. 175
Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)
Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)
Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем


Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса
Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 = 
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).
Рис. 179
Рис. 180
Рис. 181
Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).
Рис. 183
Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R



PF = 

Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP = 




Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP = 
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 = 

Ответ: а) 


18.8. Усечённый конус
Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)
Рис. 186
Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.
Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).
Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 = 
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.
Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.
Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)
Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)
т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).
Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то 




Vкон : Vпир = π : 1 или Vкон : 
Vкон = 
Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон = 
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.
Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V = 






 — диаметр основания конуса;
— диаметр основания конуса; — радиус дуги выкройки;
— радиус дуги выкройки; — центральный угол выкройки.
— центральный угол выкройки. — радиус внешней дуги выкройки;
— радиус внешней дуги выкройки; — радиус внутренней дуги выкройки;
— радиус внутренней дуги выкройки;






































