Как найти угол разворота

14. Определение радиуса разворота по углу крена и скорости разворота.

Задача
решается по формуле:

где
π’
— радиус разворота самолета в м

V
—
скорость полета самолета в м/сек;

g—
ускорение силы тяжести, равное 9,81м/сек².

Порядок
решения
(шкалы 4,
5
и 6):

— установить
визирку по шкале 6
на деление, соответствующее скорости
полета самолета
V*
в км/час (рис.
48);_______________________________________________________

*
Устанавливаемое
значение V
может
быть уменьшено в 10 или 100 раз.

— передвигая
движок, подвести под визирку деление
шкалы 4,
соответствующее углу крена самолета
β;

— отсчитать
по шкале 5
против индекса ® искомое значение
радиуса разворота самолета R
в
км
или
м.
(Ключ
для решения этой задачи помещен на
линейке, слева от шкалы 3.)

Примеры.
1)
Дано: V
=650 км/час;
β
= 15°.

Находим:
R
= 12,4
км

2)
Дано: V
— 230
км/час;
β
= 30°.

Находим:
R
= 720 м.

15. Определение времени разворота самолета с заданным радиусом и скоростью разворота

Задача
решается по формулам:

где
π = 3,14;

R
—
радиус разворота в км
или м;

V
—
скорость разворота в км/час
или м/сек;

УР
—
угол разворота самолета.

Порядок
решения (шкалы 1
и 2):

— установить
визирку по шкале 1
на деление, соответствующее скорости
полета самолета V
в
км/час
(рис.
49);

— передвигая
движок, подвести под визирку деление
шкалы 2,
соответствующее радиусу разворота R;

— отсчитать
по шкале 2
против индекса t₃₆₀
искомое
время разворота самолета на 360°.

Примеры.
Дано:
1) V
=
700 км/час;
R
=
8,5 км.
Находим:
t₃₆₀
=
4 мин. 35 сек.

2) Дано:
V
= 450
км/час;
R
= 6,5 км. Находим:
t₃₆₀
= 5 мин. 26 сек.

3) Дано:
V
= 240 км/час;
R
= 1500
м.
Находим:
t₃₆₀
— 2 мин. 22 сек.

Примечания:
1.
При радиусе разворота до 10 км
скорость
уменьшать в 10 раз и устанавливать на
втором интервале шкалы 1; радиус разворота
увеличивать в 10 раз и устанавливать на
втором интервале шкалы 2.

2.
При радиусе разворота более 10 км
скорость
уменьшать в 100 раз и устанавливать на
первом интервале шкалы 1, а радиус
разворота в км
устанавливать
на первом интервале шкалы 2.

Для определения
времени разворота на любой угол
необходимо:

— определить время
разворота на 360°, как указано выше;

— установить
визирку по шкале 1
наделение, соответствующее значению
360 (рис. 50);

— передвигая
движок, подвести под визирку по шкале
2
значение времени разворота самолета
на 360°;

— установить
визирку по шкале 1
на величину угла разворота самолета;

— отсчитать
по шкале 2
искомое значение времени разворота на
заданный угол.

Пример.
Дано:
t₃₆₀
— 5
мин. 35 сек.; УР
= 125°.
Находим: t_УР=
1
мин. 56 сек.

16. Определение времени разворота самолета с заданным креном и скоростью разворота.

Задача решается
по формуле

Порядок
решения
(шкалы 4
и 5):

— установить
визирку по шкале 5
на деление, соответствующее скорости
полета V
в
км/час
(рис.
51);

— передвигая
движок, подвести под визирку деление
шкалы 4,
соответствующее углу крена β;

— отсчитать
по шкале 5
против деления, соответствующего 10°
шкалы 4,
искомое время разворота самолета в сек.

Пример.
Дано:
V
= 450
км/час;
β
= 15°.

Находим:
t₃₆₀
⁼
295 сек. = 4 мин. 55 сек. Время разворота на
заданный угол в этом случае может быть
определено так, как показано на рис. 52.

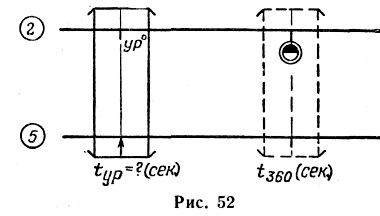
Пример.
Дано:
t₃₆₀
= 4 мин. 55 сек. = 295 сек.; УР
= 210°.

Находим:
t_УР=
173 сек. = 2 мин. 53 сек.

ЛЕКЦИЯ
№2. СИСТЕМЫ КООРДИНАТ, РАСЧЕТ ЭЛЕМЕНТОВ
ГОРИЗОНТАЛЬНОГО МАНЕВРИРОВАНИЯ.

И
так, мы подошли ко второй лекции. Мы
рассмотрим такие навигационные
элементы и понятия, которые неплохо бы
было знать начинающим навигаторам и
летчикам! Итак, попрошу чуточку внимания…начинаем
занятие!

ОСНОВНЫЕ
СИСТЕМЫ КООРДИНАТ, ПРИМЕНЯЕМЫЕ В
НАВИГАЦИИ

На
самом деле, систем координат великое
множество, как в СНГ, так и за рубежом.

 Вообще,
любую систему координат привязывают к
какому либо телу, которое максимально
повторяет очертания Земли и её
поверхности. В СНГ за такое тело принят
эллипсоид Красовского, великого
советского ученого. Он предложил
использовать его эллипсоид в 1946 году.
Кстати, он до сих пор является основным
геометрическим телом, предназначенным
для расчетов. На западе в качестве
такого тела принята система WGS
– 84, WORLD
GEO
SYSTEM,
созданная в 1984 году и рекомендованная
ИКАО.

И
так, познакомимся с основными системами
координат:

1.
ГЕОГРАФИЧЕСКАЯ СИСТЕМА КООРДИНАТ

Это
самая распространенная система
координат. Она образована сеткой
меридианов и параллелей. Координатами в
данной системе являются ШИРОТА и
ДОЛГОТА.

ШИРОТА
j
–
это угол, заключенный между плоскостью
экватора и нормалью, проведенной через
заданную точку на поверхности Земли. (нормаль
– обычная прямая, проведенная из центра
Земли к заданной точке)

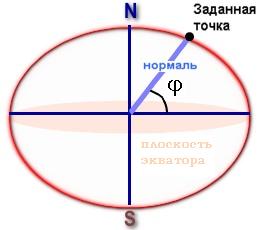
Отсчитывается
от экватора к нормали в северном
полушарии со знаком +, в южном полушарии
со знаком -. ( от –90, до +90).

Обозначается
только так:

Пол. 
Град. Мин.    
Дес. доли мин.

 
С       
72     12  
,      6                  
(естественно,
полюс и цифры пишите свои!)

Пол.
– полушарие, может быть Южное ( Ю, S),
Северное (С, N).

Например,
с 60 30, 15 – означает, Северное полушарие,
шестьдесят градусов, тридцать минут, и
шесть десятых минуты.

ДОЛГОТА
l–
это двугранный угол, образованный
плоскостью нулевого (гринвичевского)
меридиана и плоскостью меридиана,
проходящего через заданную точку.

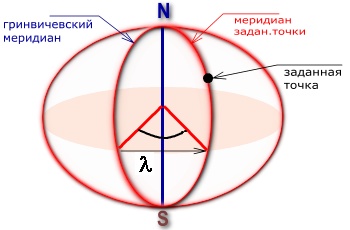
Отсчитывается
в восточном полушарии от 0 до 180 градусов,
в западном – от 0 до –180 градусов.

Обозначается
так:

Пол. 
Град.     Мин.     
Дес. доли мин

 с     
040    35     
12         (естественно,
полюс и цифры пишите свои!)

Долгота
бывает западной (З, W),
восточной (В, E).

Здесь,
все так же, как и с широтой, за
исключением, что градусы обозначаются
тремя цифрами.

На
этом, с географической системой
координат мы закончим.

Мы
не рассмотрели её подробно. В принципе,
это на данный момент не нужно. Я старался
пояснить лишь основные моменты, которые
могут помочь в навигации и
самолетовождении.

Теперь,
познакомимся с ОРТОДРОМИЧЕСКОЙ
СИСТЕМОЙ КООРДИНАТ.

2.ОРТОДРОМИЧЕСКАЯ
СИСТЕМА КООРДИНАТ

Она
образована двумя
взаимоперпендикулярными
ортодромическими линиями. Координаты
измеряются линейными величинами (метры,
километры и т.д.).

Что
значит –  образована
двумя взаимоперпендикулярными
ортодромическими линиями? Это значит,
что оси этой координатной системы –
дуги, и обе они располагаются в
плоскостях, проходящих через центр
земного шара. При небольших расстояниях
ортодромическую систему 
можно рассматривать как Декартову
систему координат. Т.Е. оси представить
не дугами, а прямыми линиями, которые
пересекаются под прямым углом.

И
так, мы подошли к разделению
ортодромической системы на две:

–        
ГЛАВНУЮ

–        
ЧАСТНУЮ

2.1.ГЛАВНООРТОДРОМИЧЕСКАЯ
СИСТЕМА КООРДИНАТ (ГОСК)

ГОСК
чаще всего используется при
маневрировании в зоне аэродрома. ГОСК
состоит из одной оси – главной
ортодромии. При маневрировании в зоне
аэродрома за главную ортодромию
принимается осевая линия ВПП. Тогда
можно получать расстояние до полосы а
так же удаление от осевой линии (т.е. –
главной ортодромии).

При
полетах по трассе с большим количеством
поворотов, главная ортодромия проходит
от аэродрома вылета, до аэродрома
посадки. При этом мы специальным
бортовым оборудованием (НАС –1, например)
можем определить расстояние до главной
ортодромии. 

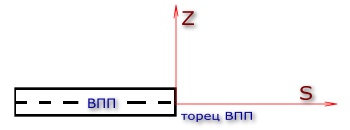
2.2.ЧАСТНООРТОДРОМИЧЕКАЯ
СИСТЕМА КООРДИНАТ (ЧОСК)

Это
самая часто используемая система при
полетах. Она может называться по-разному,
но идея одна. ЧОСК связана с конкретным
участком полета.

За
начало отсчета выбивается пункт, на
который летим, т.е. КПМ (ППМ). При этом
прямая S будет являться как бы
продолжением ЛЗП (но не самой ЛЗП!!!!), а
прямая Z – перпендикулярно ЛЗП (и S
соответственно) и направлена по ходу
полета вправо. Координата S будет со
знаком  “-“  всегда, кроме точки
прибытия – в ней  S=0.

Координата
S (ее значение по модулю) показывает
оставшееся расстояние до ППМ назначения,
или КПМ

Координата
Z показывает Линейное Боковое Уклонение
(ЛБУ). Она положительна, если ЛБУ от ЛЗП
правое, и отрицательна, если ЛБУ от ЛЗП
левое, и Z=0, если ЛБУ=0.

Ортодромическая
система координат применяется в
бортовых навигационных станциях, таких
как НАС в Ил-18, Ту-134; НВУ – Ту – 154 и т.д.

Частноортодромическая
система координат наиболее удобна. Мы в
реальном времени можем получать
сведения о местонахождении
относительно ЛЗП, если, конечно, наш
пепелац оснащен необходимым
оборудованием (о нем – в следующих
лекциях!)

ПОЛЯРНАЯ
СИСТЕМА КООРДИНАТ

 То,
что система называется полярной, ещё не
значит, что она применяется только на
полюсе! 😉

И
так, в данной системе координатами
являются:

–        
Азимут ( измеряется от северного
направления меридиана, проходящего
через опорный пункт, и направлением из
этого пункта  на ВС. Отсчитывается от 0
до 360 градусов по часовой стрелке)

–        
пеленг

–        
радиал

–        
горизонтальная дальность (ГД) –
ортодромическое расстояние от опорного
пункта до МС. Есть ещё наклонная
дальность(НД) – расстояние от опорного
пункта до ПМС)

Чем
же отличаются азимут, радиал, пеленг? –
принципиально, НИЧЕМ!!! Выбор слова
зависит от опорной точки. Если это
радиостанция, грамотнее использовать
слова пеленг или радиал.

Теперь
разберёмся с дальностью.  Чего это за
зверёк за такой?

В
практике применяют ГД, т.е. линию от
опорной точки до МС. Как её получить?
Просто!

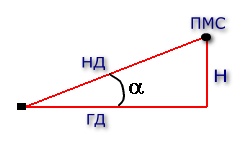
Как
видно, мы имеем треугольник,
образованный высотой полета, НД, ГД. 
НД и высоту можно посмотреть на приборах
– на высотомере и на дальномерном табло.
(если есть подобное оборудование).
Соответственно, ГД можно получить двумя
способами:

–        
по теореме Пифагора

–        
через угол Альфа

По
теореме Пифагора, формула выглядит так:
ГД2=НД2-H2

Соответственно,
необходимо только корень извлечь (см.
ПРАКТИКА в конце лекции)

Если
ищем по углу Альфа, то формулы следующие:

a=H
/ НД

ГД=НД
х cosa

Единственно,
если НД больше 5 – ти высот полета, то её
приблизительно считают равной ГД.

Вот,
собственно, и все!

Единственно,
при полетах обычно используют несколько
систем координат. Скажем, когда Командир
Воздушного Судна (КВС) просит штурмана
указать местоположение, то штурман
называет координаты в географической
системе координат и положение ВС
относительно трассы (это просто пример).

Теперь
приступим ко второй части лекции.

РАСЧЕТ
ЭЛЕМЕНТОВ ГОРИЗОНТАЛЬНОГО
МАНЕВРИРОВАНИЯ.

 Я
думаю, что такое горизонтальное
маневрирование, все знают! (это когда
самолет поворачивает). Чтобы не сойти с
ЛЗП при повороте, чтобы узнать, сколько
времени потребуется для совершения
разворота необходимо произвести
специальные расчеты. Как их произвести,
я сейчас расскажу:

И
так, имеем картинку:

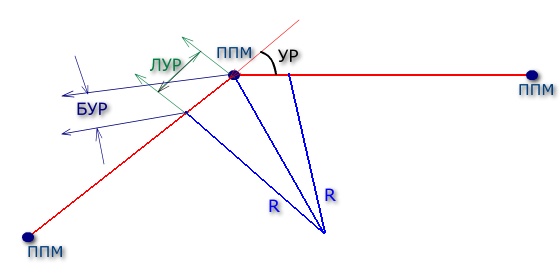
Основными
элементами при маневрировании являются:

1.Радиус
разворота.

Для
его расчетов требуется знать истинную
скорость ВС (о скоростях читайте в
следующих лекциях) и крен, с которым мы
будем выполнять разворот.

Формула
для расчета радиуса выглядит так:

R=
W² / (g x tgq),

где
W –
путевая скорость ВС, g
– 9.81 (знакомое число? Ну-ка, вспомним
школу, ага, курс физики! J
)., tgq
– тангенс крена ВС.

ПРИМЕЧАНИЕ!!!!!!!!!!

Скорость,
прежде, чем возводить в квадрат
необходимо перевести в мс.
Соответственно, радиус разворота мы
получим в метрах, которые для дальнейших
расчетов необходимо перевести в
километры, поделив ответ на 1000.

2.Угол
разворота.

УГОЛ
РАЗВОРОТА (УР) –
угол, на который разворачивается
продольная ось самолета при переходе с
одной ЛЗП на другую.

В
связи с тем, что на картах публикуется
ЗМПУнач, то УР можно примерно определить
по их разности:

УР=ЗМПУ²н
– ЗМПУ¹к

3.
Линейное упреждение разворота. ЛУР.

Это
то расстояние до ППМ, которое необходимо
не долетать, чтобы вписаться в поворот.

ЛУР=
R
x
tg (УР2)

4.
Боковое упреждение разворота. БУР.

БУР
= ЛУР х sinУР

5.
Время разворота.

Ну,
время разворота – это понятно. Время, за
которое самолет повернет на нужный угол.

t₃₆₀
= (УР 360) х (2ПR
V)

Где
УР – необходимый угол разворота, П = 3.14, R
– радиус разворота, V  – истинная скорость.

И
так, по теории – всё!

Теперь
приступим к практическим занятиям!

ПРАКТИКА

И
так, порешаем задачки вместе!

ЗАДАЧА№1.

Определить
ГД, зная Н и НД.

Н
= 10км.

НД
= 70км.

ГД-?

Решение:

И
так, начнем.

Сначала
найдем угол Альфа:

Arcsin
= HНД =
8.2132 (*)

Затем,
ГД:

ГД
= НД х cosАльфа
= 69.282 (км)

Вот
и ответ! Видите, отличие ГД от НД
составляет всего 718 метров! Так что этим
можно было пренебречь!

ЗАДАЧА№2.

Найти
время полета на маршруте, состоящего из
двух участков.

ДАНО:

W=500кмч

g=9.81

Крен
= 15*

ЗМПУ1=60*

ЗМПУ2=30*

S1=150км

S2=70км

НАЙТИ:

t
полета

РЕШЕНИЕ:

Сначала,
найдем радиус разворота:

1.переведем
скорость из кмч в  мс
.

W=
500 3.6 = 138.89 мс

Затем,
по формуле, получим радиус:

138.89²
9.81 х tg15
= 7338.72 метра

.

УР
приблизительно равно ЗМПУ2 – ЗМПУ1 = 30* (УР
берем по модулю)

Теперь,
найдем ЛУР

7338.72
х tg15 =
1966.4 метра. То есть почти два километра.

Так.
Теперь, учитывая ЛУР, рассчитаем время
полета на участке №1.

S_с
ЛУР = S1
– ЛУР = 150 – 1.9664 = 148.0336 километра. (не
забываем про переводы!)

t₁=S_cЛУР
W = 148.0336
500 = 0.296 от часа, или 17.76 минуты. Это
первый участок.

S_с
ЛУР2=S2
– ЛУР = 68.0336 километра.

t₂=
S_{с ЛУР2}
W =
68.0336 500 = 0.136 часа, или 8.16 минуты.

Ну,
и общее время равно сумме времени на
двух участках и равно 25.95 минуты.

Все,
задача решена!

Вопрос
– почему из второго участка нужно ЛУР
вычитать? – ответ – при повороте
траектория полета самолета
представляет часть окружности.
Соответственно, при отсутствии ветра
ЛУР перед ППМ будет равен отрезку за ППМ
(ЛУР обратный) – см.рисунок!

Так
же в решении задач совсем не нужно
приходить к такой точности, как это
делал я – ведь я это делал только для
наглядности!

ПОСЛЕСЛОВИЕ

В
данной лекции мы коротко рассмотрели
основные системы координат, которые
могут помочь как в навигации, так и в
самолетовождении. На данном этапе,
лекция может показаться непонятной – НО
полученные знания ОЧЕНЬ пригодятся в
освоении навигационных систем, в
частности НАС – 1, о которой я просто
обязан рассказать, но чуть позже.

Помимо
координат, мы рассмотрели и элементы
расчетов горизонтального
маневрирования. Основным элементом 
является ЛУР – так как он очень
важен, особенно при полетах на ВС от 3-го
класса и далее.

В
следующей лекции мы рассмотрим ветер и
его влияние на полет!

Все
вопросы присылайте мне на мыло.

До
встречи!!!!

Автор:
Александр Захаров

Мыло:
A.Zaharov@rambler.ru

Скачать WORD-версию

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О, в результате чего получается точка А1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А). При этом точка А1 лежит на окружности с центром в точке О радиуса ОА. Другими словами, когда точка А осуществляет поворот относительно точки О, она переходит в точку А1, лежащую на окружности с центром О радиуса ОА.

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О, она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса ОА.

Изобразим графически поворот точки А относительно точки О, перемещение точки А в точку А1 отметим стрелкой:

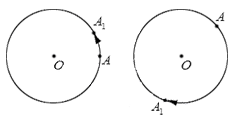
Полный оборот

Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А, пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О.

Проиллюстрируем:

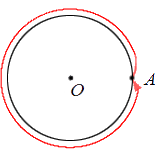
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

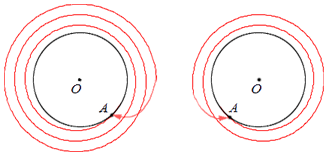
В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О. Любую точку окружности с центром О можно рассматривать как точку А1, полученную в результате поворота точки А. Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от -∞ до +∞, что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180°.

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α, β, γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α1, α2, α3…..αn.

Разберем характеристики угла поворота подробнее.

Направление поворота

Отметим на окружности с центром О точки А и А1. В точку А1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

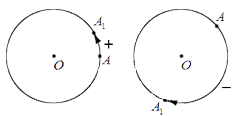
Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от -∞ до +∞;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0°. Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0° точка A остается на месте.

Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А1. В таком случае абсолютная величина угла АОА1, выраженная в градусах, не превосходит 180. Если поворот имел положительное направление, то величина угла поворота считается равной величине угла АОА1; если отрицательное – величина угла поворота равна величине угла АОА1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30°, 180° и -150°:

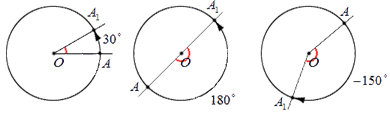
Углы поворота, превышающие 180 или меньшие –180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45°, затем еще на 60° и еще раз – на -35°. Обозначим промежуточные точки поворотов А1, А2 и А3. В конечную точку А3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45°+ 60° + (-35°) = 70°. Проиллюстрируем:

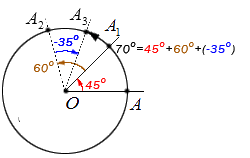
Таким, образом, углы, превышающие 180°, будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298° соответствует последовательным поворотам на 180° и 118°, или 90°, 90°, 90° и 28°, или 180°, 180° и -62°, или 298 последовательных поворотов на 1°.

По такому же принципу определяются углы меньше -180°. Например, угол поворота -515° можно определить, как последовательные повороты на -180°,-180° и -155°.

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от -∞ до +∞. Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360° или 2π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в -360° или -2π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от -180° до 180°. К примеру, поворот осуществляется на 1478°. Представим эту величину как: 360 · 4 + 38, т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38°. Или еще один пример: угол поворота в -815° можно представить, как (-360) · 2 + (-95), т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на -95°.

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

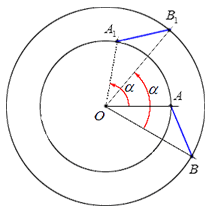
Как пример, иллюстрируем следующее действие: поворот отрезка АВ на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А1В1.

Вращательное движение (Движение тела по окружности)

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

Угол поворота

Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

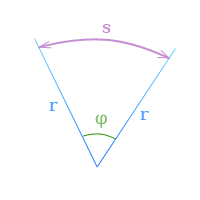
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана

[
φ = frac{s}{r}
]

Соотношение между единицами угла

[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]

$ 1 enspace рад = 57.3° $

$ 1° = 17.45 enspace мрад $

$ 1´ = 291 enspace мкрад $

Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.

Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).

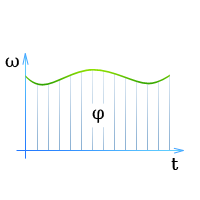
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то

Период

[
T = frac{1}{f} = frac{1}{n}
]

Угловое перемещение

Угловое перемещение равно произведению полного числа оборотов на 2π:

[
φ = 2 π N
]

Угловая скорость

Из формулы для одного оборота следует:

[
ω = 2 π f = frac{2π}{T}
]

Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.

Вращательное движение (движение тела по окружности)	стр. 422

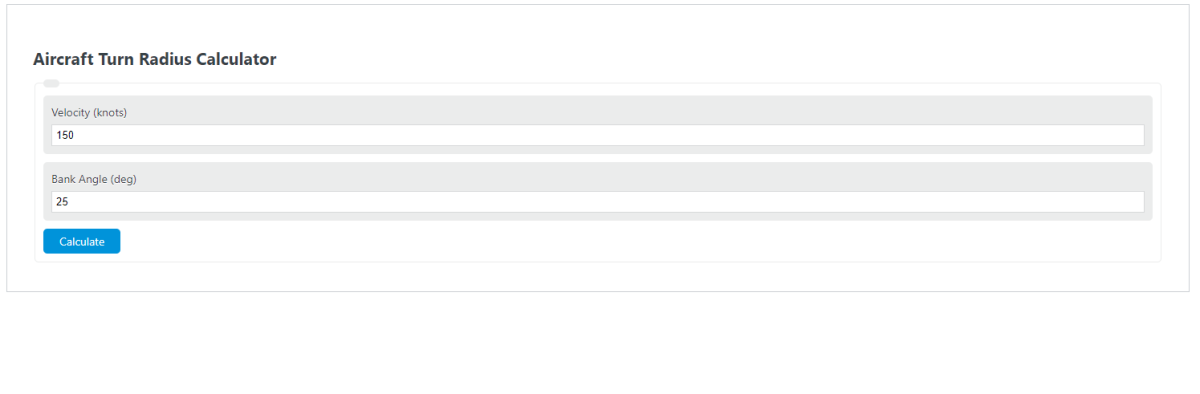
Unit Converter