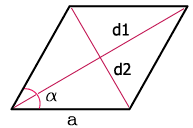
Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачу из задания №23 ОГЭ по математике. Это геометрическая задача на вычисление. Бояться второй части ОГЭ не надо. Задание №23 оно почти такое же по простоте, как и задачи из первой части ОГЭ Единственное требование – это написать решение задачи, а не угадать ответ. Давайте начнем.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба
Построим рисунок и запишем дано
Решение
1) Так как диагонали в параллелограмме точкой пересечения делятся пополам, то
2) Рассмотрим треугольник АОК – прямоугольный. АО=30, ОК = 15 (по условию), значит по свойству прямоугольного треугольника (если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов). Получаем, что:
3) Диагонали в ромбе делят углы пополам, значит:
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Ромб в окружности найти угол
Точка O — центр окружности, на которой лежат точки A, B и C таким образом, что OABC — ромб. Найдите угол OCB. Ответ дайте в градусах.
Проведём диагональ BO Рассмотрим треугольник OBC, OB и OC равны как радиусы окружности. Все стороны ромба равны, поэтому BC = OC, получаем, что OC = BC = BO, следовательно, треугольник BOC — равносторонний, поэтому все его углы, в том числе и угол OCB, равны 60°.
Радиус и угол ромба
Свойства
Радиус вписанной окружности, представляющий собой половину высоты, теоретически участвует в образовании прямоугольного треугольника, из которого можно найти сторону ромба, как отношение удвоенного радиуса к синусу угла α. a=2r/sin〖α 〗
Высота ромба будет равна удвоенному радиусу вписанной окружности. Площадь, ка произведение высоты и стороны ромба, через радиус вписанной окружности и угол α будет представлена произведением соответствующих выражений. Чтобы вычислить периметр, нужно будет эквивалент стороны умножить на четыре. h=2r S=(4r^2)/sin〖α 〗 P=8r/sin〖α 〗
Углы ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).
Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac<large h> <large a>) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac<large h><large sin alpha>=frac<large a><large sin 90°>.) | (3) |
| (small sin alpha=frac<large h><large a>) | (4) |
| (small alpha=mathrmfrac<large h><large a>) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).
Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac<large h^2><large S>, ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac<large h><large a>=mathrmfrac<large h><large frac |
(9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).
Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac<large S><large a^2>. ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.
| (small h=frac<large d_1d_2><large sqrt>.) | (11) |
| (small a=frac<large sqrt><large 2>.) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac<large h><large a>) ( small =frac<frac<large d_1d_2><large sqrt>><frac<large sqrt><large 2>> ) ( small =frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (13) |
| (small alpha=mathrm frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).
Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac<alpha> <2>.) Тогда для треугольника AOB имеют места следующие равненства:
(small frac<large AO><large a>=sin frac<alpha><2>,)
(small frac<large AO><large a>=cos frac<beta><2>)
| (small sin frac<alpha><2>=frac<large d><large 2a>) | (15) |
| (small cos frac<beta><2>=frac<large d><large 2a >.) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac<alpha><2>=±sqrt<frac<large 1-cos alpha><large 2 >>,) | (17) |
| (small cosfrac<beta><2>=±sqrt<frac<large 1+cos beta><large 2 >>.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac<alpha><2>,) | (19) |
| (small cos beta=2cdot sin^2 frac<beta><2>-1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac<large d^2><large 2a^2>,) | (21) |
| (small cos beta=frac<large d^2><large 2a^2>-1.) | (22) |
| (small alpha=mathrm left(1- frac<large d^2> <large 2a^2>right),) | (23) |
| (small beta=mathrm left( frac<large d^2><large 2a^2>-1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.
В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac<large 2 cdot r><large a>) | (26) |
| (small alpha=mathrmfrac<large 2 cdot r><large a>) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
[spoiler title=”источники:”]
http://geleot.ru/education/math/geometry/calc/rhombus/radius_and_angle
http://matworld.ru/geometry/ugly-romba.php
[/spoiler]
Ромб – геометрическая фигура, представляющая собой отдельную разновидность параллелограмма. Все
имеющееся стороны равны между собой. Геометрическая фигура представляет собой отдельную
разновидность параллелограмма. Все имеющееся стороны равны между собой. Чтобы исключить риски
недопонимания, а также освоить принципы расчетов, рекомендуется ознакомиться с некоторыми
особенностями подробней.
- Острый угол ромба через длинную диагональ и сторону
- Острый угол ромба через короткую диагональ и сторону
- Тупой угол ромба через длинную диагональ и сторону
- Тупой угол ромба через короткую диагональ и сторону
- Острый угол ромба через диагонали
- Угол ромба через площадь и сторону
- Острый угол ромба через радиус вписанной окружности в ромб
и площадь ромба - Острый угол ромба через высоту и сторону
- Половинный угол ромба через высоту и диагональ
- Половинный острый угол ромба через диагонали
- Половинный тупой угол ромба через диагонали
Острый угол ромба через длинную диагональ и сторону
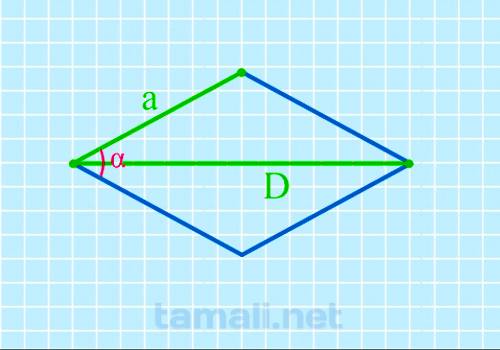
Для проведения расчетов используется формула:
cos α = D² / 2a² — 1
где D — длинная диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Предположим, что длинная диагональ 25 мм, сторона – 15 мм. Отталкиваясь от
полученных сведений, результат получается следующим: cos α = 25² / 2 х 15² — 1 = 67.11º
Тупой угол ромба через длинную диагональ и сторону
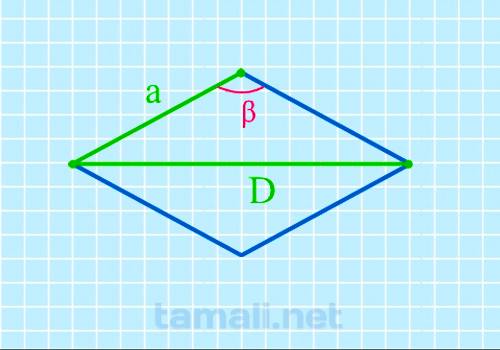
Имея достоверные данные о значение длинной диагонали (D) и стороне (a), порядок вычисления не
предполагает под собой каких-либо сложностей с определением. Для этого в геометрии предлагается
воспользоваться следующей формулой:
cos β = D² / 2a² — 1
Цифр после
запятой:
Результат в:
Пример. Предположим, D = 60 мм, a = 90 мм. Исходя из полученных сведений, расчет по
имеющейся формуле имеет вид: cos β = 60² / 2 х 90² — 1. В таком
случае cos β = 141.05. При условии, что D>a, решение не представляется возможным.
Острый угол ромба через короткую диагональ и сторону
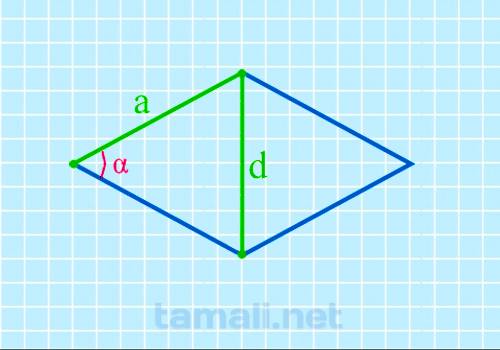
Для проведения интересующегося расчета требуется знать данные о короткой диагонали (d) и стороне (a).
При условии наличия используемая формула имеет следующий вид:
cos α = 1 – d² / 2a²
где d — короткая диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Из представленной формулы следует, что инициировать получение интересующих
данных не вызывает сложностей. Чтобы удостовериться в этом, достаточно рассмотреть пример. Допустим,
что d = 40 мм, a = 25 мм. В таком случае определение результата осуществляется следующим образом:
cos α = 1 – 40² / 2 х 25².
Используя калькулятор, становится известно,
что cos α = 106.26. Подтвердить подлинность результата можно в режиме онлайн через
специализированный сервис вычислений.
Острый угол ромба через диагонали
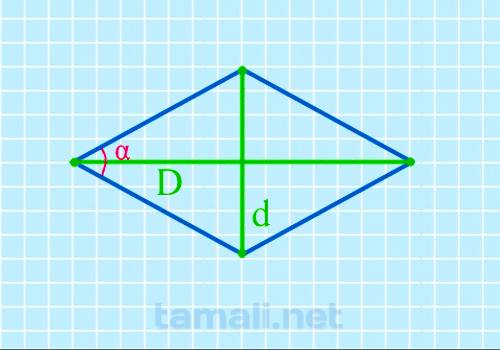
Представленный параметр расчета по праву считается одним из наиболее сложных. Чтобы исключить риски
допущения ошибок и недопонимания, рекомендуется ответственно подходить к организации вычислений.
Чтобы узнать информацию, чему равняется sin α, достаточно воспользоваться следующей формулой:
sin α = (2 · Dd)/ (D² + d²)
где D является длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Во время определения sin α оптимальным решением станет использование стандартных математических
правил. Они предполагают первичное умножение, после чего деление. Суммирование осуществляется на
завершающем этапе определения значения.
Пример. Предположим, D = 85 мм, d = 15 мм. Имеющиеся значения требуется подставить в
формулу. В итоге получается: sin α = (2 · 85)/85² + 15². Используя
автоматизированный калькулятор для геометрии, получается, что sin α = 20.01
Тупой угол ромба через короткую диагональ и сторону
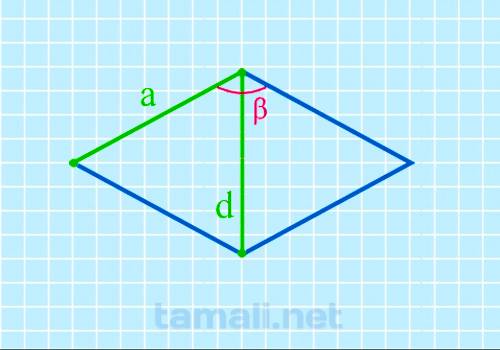
Порядок вычисления предполагает использование соответствующей формулы. Чтобы инициировать расчет
требуется знать точные данные относительно короткой диагонали (d) и стороне (a). В таком случае
расчет проходит следующим образом:
cos β = 1 — d² / 2a²
где d — короткая диагональ, a — сторона ромба.
Цифр после
запятой:
Результат в:
Пример. Предположим, что d = 27 мм, a = 65 мм. Используя имеющуюся формулу,
вычисление проходит по следующей процедуре: cos β = 1 — 27²/2х65².
Используя стандартные принципы
вычисления либо специализированный онлайн калькулятор, cos β = 23.98. Чтобы гарантировать
достоверность вычислений настоятельно рекомендуется выполнять проверку полученных данных несколькими
способами.
Острый угол ромба через радиус вписанной окружности в ромб и площадь ромба
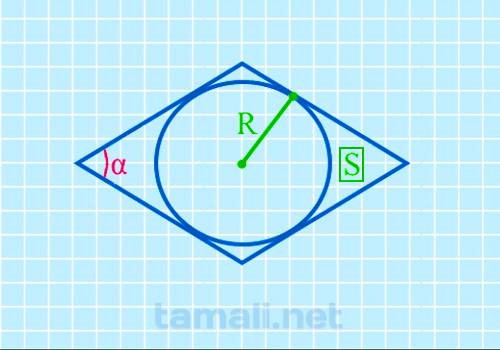
Принципы определения интересующей величины предполагают необходимость использования следующей
формулы:
sin(α) = 4R²/S
где R – радиус, S – заявленная площадь геометрической фигуры.
Цифр после
запятой:
Результат в:
Пример. Предположим, что радиус составляет 2 см, заявленная площадь 20 мм² .
Подставив имеющиеся значения в формулу, имеем следующий вид: sin(α) = 4 х 2²/20 = 53º.
Угол ромба через площадь и сторону
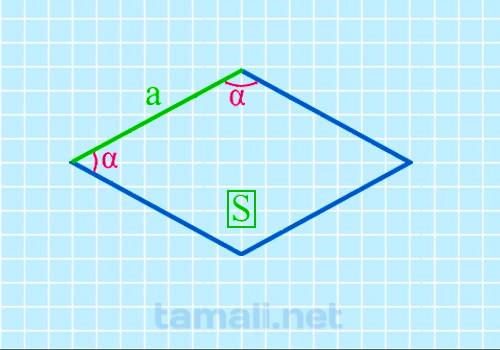
Представленный метод часто используется, чтобы узнать интересующий параметр. Главное условие –
наличие известных величин из формулы, которая имеет следующий вид:
sin(α) = S/a²
где S является площадью ромба, a — стороной.
Цифр после
запятой:
Результат в:
Рассмотрим порядок определения неизвестной величины на конкретном примере. Допустим, что S = 65 мм² ,
a – 12 мм. В таком случае, получается: sin(α) = 65/12³ = 26,83º.
Острый угол ромба через высоту и сторону
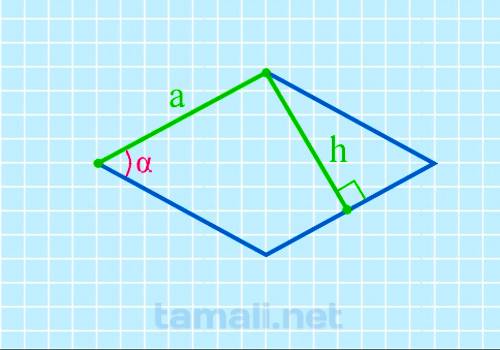
Для определения синуса предполагается использование следующей несложной формулы:
sin(α) = h / a
где h – заявленные показатели высоты, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Допустим, что высота составляет 9, сторона – 15. Следовательно, вычисления
осуществляются следующим образом: sin(α) = 9/15 = 36.86 градусов.
Половинный угол ромба через высоту и диагональ
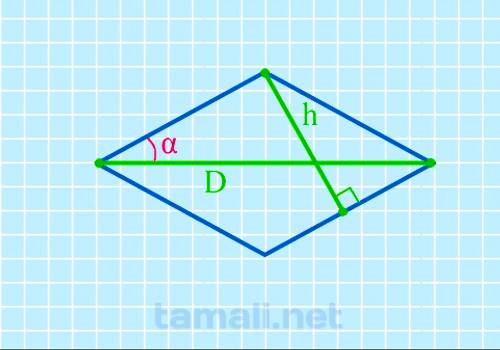
Чтобы отыскать интересующий синус, требуется воспользоваться следующим правилом определения
величины:
sin( α/2 ) = h/D
где h – имеющаяся высота, D – заявленная длина диагонали.
Цифр после
запятой:
Результат в:
Пример. Высота 43, диагональ 76. Следовательно, sin( α/2 ) = 43/76 = 34.4.
Половинный тупой угол ромба через диагонали
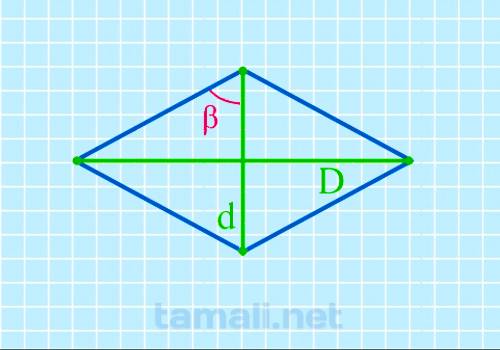
Использование рассматриваемого метода не предполагает под собой существенных сложностей. Достаточно
воспользоваться специально разработанной формулой, которая имеет следующий вид:
tg( β/2 ) = D / d
где D выступает длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Пример. Достаточно подставить для вычисления имеющиеся данные, чтобы в конечном
итоге получить искомый результат. К примеру, D = 80 мм, d = 35 мм. Используя стандартные принципы
вычисления получается: tg( β/2 ) = 80/35 = 66.37
Половинный острый угол ромба через диагонали
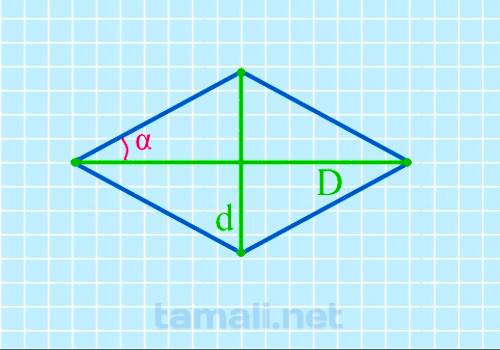
Проведение расчетов с помощью представленной методики требует наличия всех переменных, среди которых
короткая и длинная диагонали. Если все необходимые параметры известны, вычисление осуществляется по
представленной формуле:
tg( α/2 ) = d / D
где D,d – заявленная длина диагоналей.
Цифр после
запятой:
Результат в:
Пример. Предположим, что D = 15 мм, d = 50 мм. Подставим имеющие значения в формулу,
имеем вид: tg( α/2 ) = 50 /15 С помощью несложных подсчетов получается, что tg( α/2 ) = 73.3
градуса.
Ромб представляет собой параллелограмм, который имеем равные стороны. При наличии исключительно
прямых углов – квадрат.
Дополнительно выделяют следующие признаки:
- имеющиеся диагонали ромба перпендикулярны;
- диагонали ромба выступают биссектрисами его углов;
- сумма квадратов всех диагоналей приравнивается к квадраты стороны, которая умножается на 4.
Чтобы параллелограмм считался ромбом, крайне важно соблюдение одного из нескольких условий, к которым
принято относить:
- все имеющиеся стороны геометрической фигуры равны между собой;
- диагонали пересекаются исключительно под прямым углом;
- диагонали геометрической фигуры выступают биссектрисами углов.



Найти углы ромба зная диагональ и длину стороны
Введите сторону ромба (a) и диагональ (d).
Формула расчёта углов ромба зная диагональ и длину стороны:
cos(α)=d2/(2*a2), β=(360-α*2)/2.
Косинус α равен, диагональ в квадрате разделённое на сторону, в квадрате, умноженное на два. Угол β – вычитаем из 360 градусов угол α умноженный на два, всё это делим на два.
| Диагональ ромба (d) | ||
| Сторона ромба (a) |
Площадь ромба
Периметр ромба
Длина сторон ромба через диагонали
Найти высоту ромба через сторону и угол
Найти диагонали ромба зная длину стороны и угол
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |