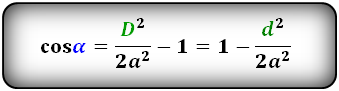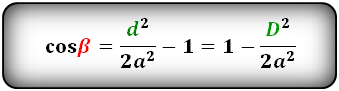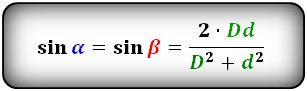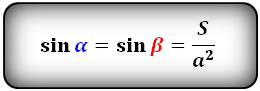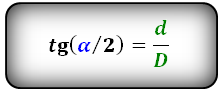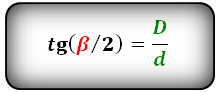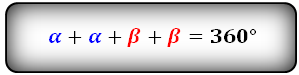Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
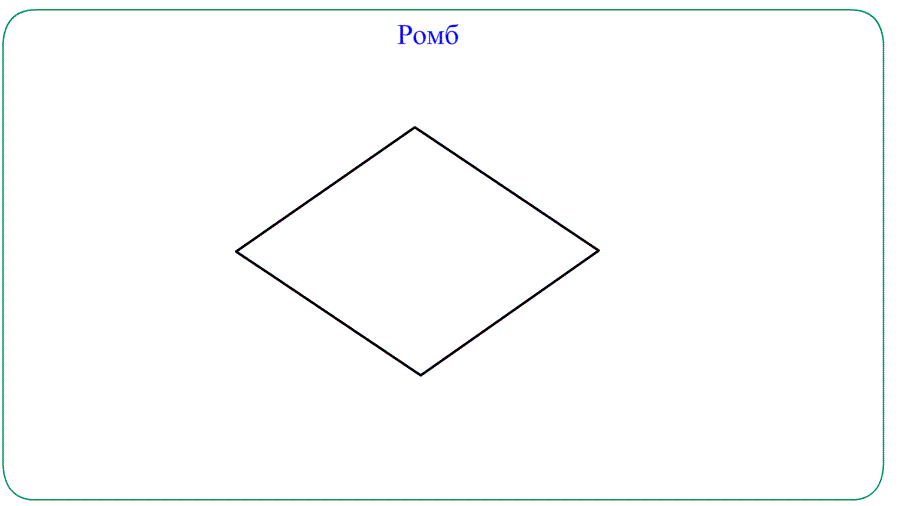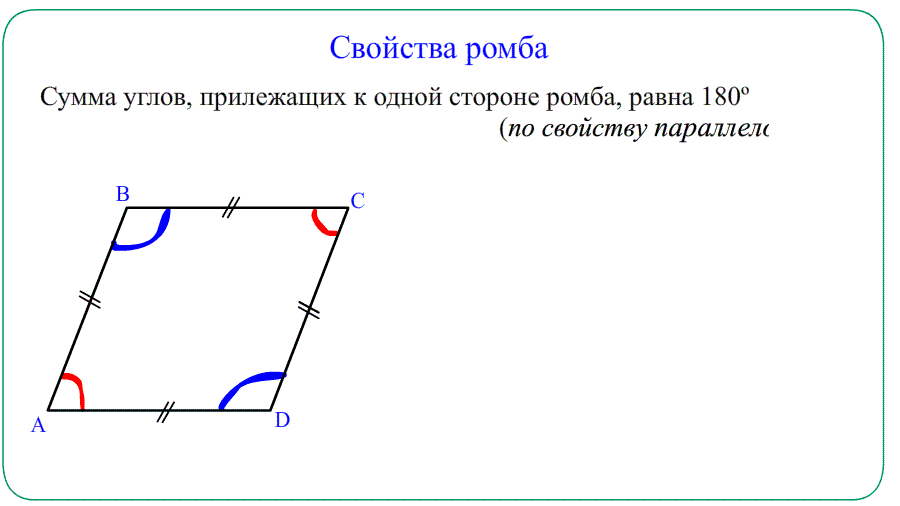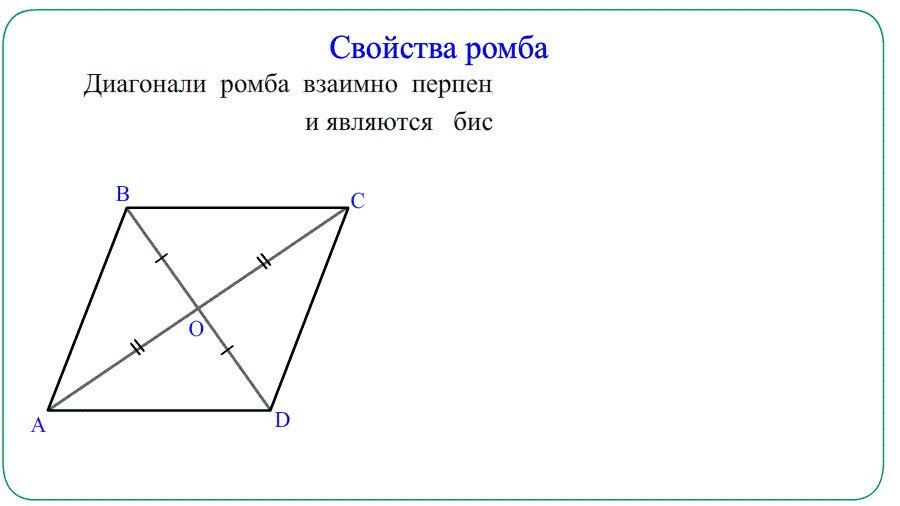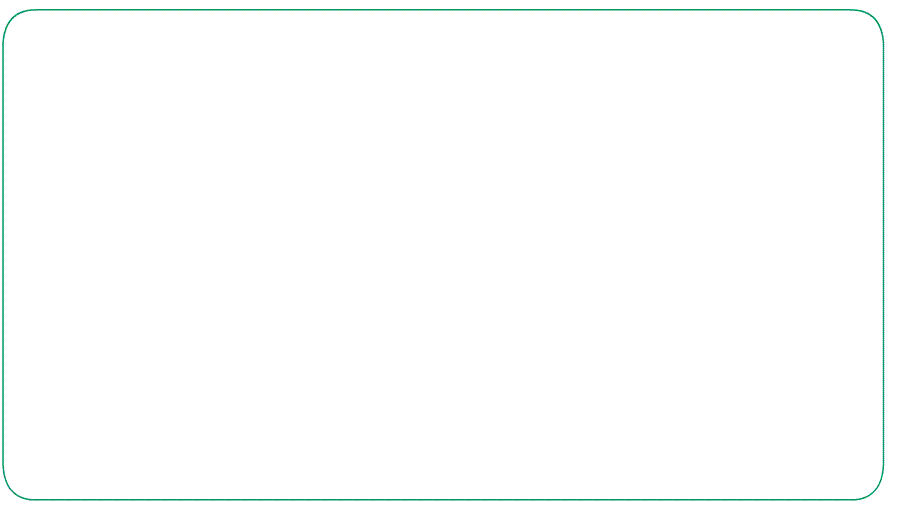
Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 25 ноября 2011
-
Обновлено: 13 августа 2021
Учебник
Геометрия, 11 класс
Ромб: Свойства, Формулы. Задачи
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая – $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . – половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ – пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
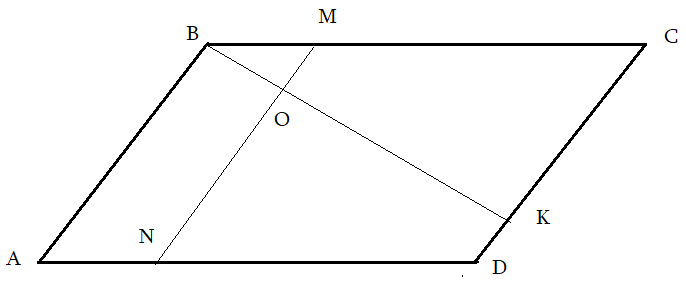
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ – параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ – квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая – $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . – половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ – пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ – параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ – квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто неподвижное – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Квадрат – одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: “В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник – стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачу из задания №23 ОГЭ по математике. Это геометрическая задача на вычисление. Бояться второй части ОГЭ не надо. Задание №23 оно почти такое же по простоте, как и задачи из первой части ОГЭ Единственное требование – это написать решение задачи, а не угадать ответ. Давайте начнем.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба
Построим рисунок и запишем дано
Решение
1) Так как диагонали в параллелограмме точкой пересечения делятся пополам, то
2) Рассмотрим треугольник АОК – прямоугольный. АО=30, ОК = 15 (по условию), значит по свойству прямоугольного треугольника (если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов). Получаем, что:
3) Диагонали в ромбе делят углы пополам, значит:
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Ромб – геометрическая фигура, представляющая собой отдельную разновидность параллелограмма. Все
имеющееся стороны равны между собой. Геометрическая фигура представляет собой отдельную
разновидность параллелограмма. Все имеющееся стороны равны между собой. Чтобы исключить риски
недопонимания, а также освоить принципы расчетов, рекомендуется ознакомиться с некоторыми
особенностями подробней.
- Острый угол ромба через длинную диагональ и сторону
- Острый угол ромба через короткую диагональ и сторону
- Тупой угол ромба через длинную диагональ и сторону
- Тупой угол ромба через короткую диагональ и сторону
- Острый угол ромба через диагонали
- Угол ромба через площадь и сторону
- Острый угол ромба через радиус вписанной окружности в ромб
и площадь ромба - Острый угол ромба через высоту и сторону
- Половинный угол ромба через высоту и диагональ
- Половинный острый угол ромба через диагонали
- Половинный тупой угол ромба через диагонали
Острый угол ромба через длинную диагональ и сторону
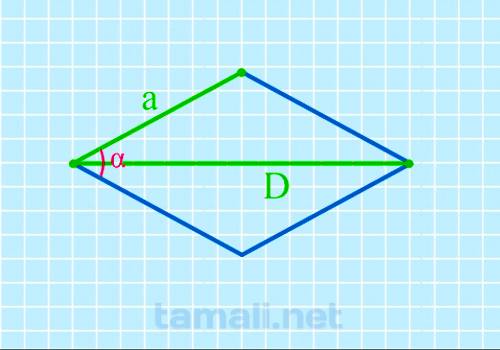
Для проведения расчетов используется формула:
cos α = D² / 2a² — 1
где D — длинная диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Предположим, что длинная диагональ 25 мм, сторона – 15 мм. Отталкиваясь от
полученных сведений, результат получается следующим: cos α = 25² / 2 х 15² — 1 = 67.11º
Тупой угол ромба через длинную диагональ и сторону
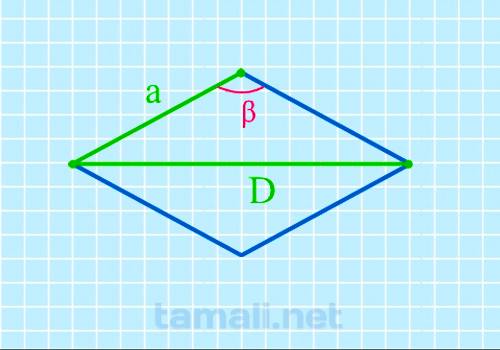
Имея достоверные данные о значение длинной диагонали (D) и стороне (a), порядок вычисления не
предполагает под собой каких-либо сложностей с определением. Для этого в геометрии предлагается
воспользоваться следующей формулой:
cos β = D² / 2a² — 1
Цифр после
запятой:
Результат в:
Пример. Предположим, D = 60 мм, a = 90 мм. Исходя из полученных сведений, расчет по
имеющейся формуле имеет вид: cos β = 60² / 2 х 90² — 1. В таком
случае cos β = 141.05. При условии, что D>a, решение не представляется возможным.
Острый угол ромба через короткую диагональ и сторону
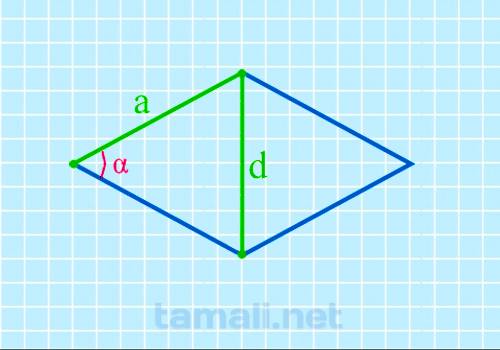
Для проведения интересующегося расчета требуется знать данные о короткой диагонали (d) и стороне (a).
При условии наличия используемая формула имеет следующий вид:
cos α = 1 – d² / 2a²
где d — короткая диагональ, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Из представленной формулы следует, что инициировать получение интересующих
данных не вызывает сложностей. Чтобы удостовериться в этом, достаточно рассмотреть пример. Допустим,
что d = 40 мм, a = 25 мм. В таком случае определение результата осуществляется следующим образом:
cos α = 1 – 40² / 2 х 25².
Используя калькулятор, становится известно,
что cos α = 106.26. Подтвердить подлинность результата можно в режиме онлайн через
специализированный сервис вычислений.
Острый угол ромба через диагонали
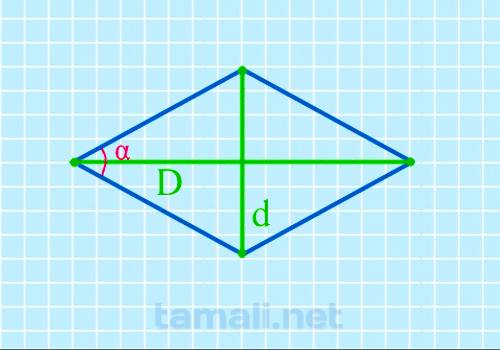
Представленный параметр расчета по праву считается одним из наиболее сложных. Чтобы исключить риски
допущения ошибок и недопонимания, рекомендуется ответственно подходить к организации вычислений.
Чтобы узнать информацию, чему равняется sin α, достаточно воспользоваться следующей формулой:
sin α = (2 · Dd)/ (D² + d²)
где D является длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Во время определения sin α оптимальным решением станет использование стандартных математических
правил. Они предполагают первичное умножение, после чего деление. Суммирование осуществляется на
завершающем этапе определения значения.
Пример. Предположим, D = 85 мм, d = 15 мм. Имеющиеся значения требуется подставить в
формулу. В итоге получается: sin α = (2 · 85)/85² + 15². Используя
автоматизированный калькулятор для геометрии, получается, что sin α = 20.01
Тупой угол ромба через короткую диагональ и сторону
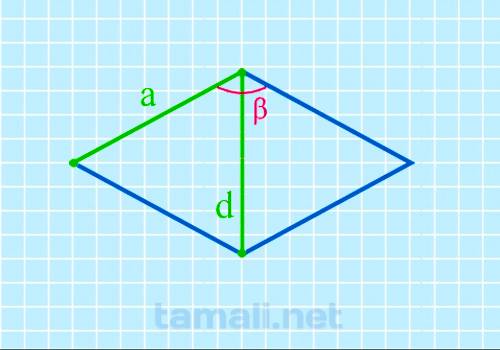
Порядок вычисления предполагает использование соответствующей формулы. Чтобы инициировать расчет
требуется знать точные данные относительно короткой диагонали (d) и стороне (a). В таком случае
расчет проходит следующим образом:
cos β = 1 — d² / 2a²
где d — короткая диагональ, a — сторона ромба.
Цифр после
запятой:
Результат в:
Пример. Предположим, что d = 27 мм, a = 65 мм. Используя имеющуюся формулу,
вычисление проходит по следующей процедуре: cos β = 1 — 27²/2х65².
Используя стандартные принципы
вычисления либо специализированный онлайн калькулятор, cos β = 23.98. Чтобы гарантировать
достоверность вычислений настоятельно рекомендуется выполнять проверку полученных данных несколькими
способами.
Острый угол ромба через радиус вписанной окружности в ромб и площадь ромба
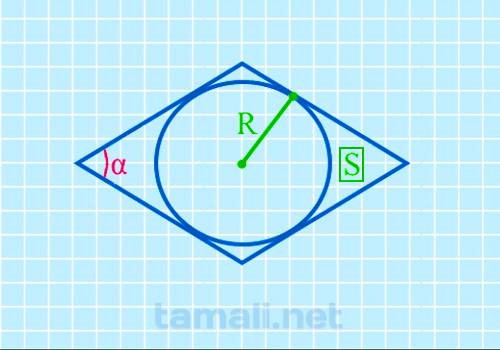
Принципы определения интересующей величины предполагают необходимость использования следующей
формулы:
sin(α) = 4R²/S
где R – радиус, S – заявленная площадь геометрической фигуры.
Цифр после
запятой:
Результат в:
Пример. Предположим, что радиус составляет 2 см, заявленная площадь 20 мм² .
Подставив имеющиеся значения в формулу, имеем следующий вид: sin(α) = 4 х 2²/20 = 53º.
Угол ромба через площадь и сторону
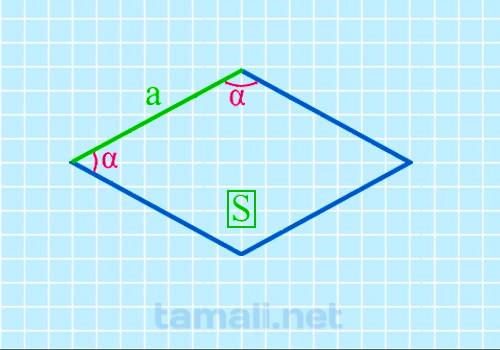
Представленный метод часто используется, чтобы узнать интересующий параметр. Главное условие –
наличие известных величин из формулы, которая имеет следующий вид:
sin(α) = S/a²
где S является площадью ромба, a — стороной.
Цифр после
запятой:
Результат в:
Рассмотрим порядок определения неизвестной величины на конкретном примере. Допустим, что S = 65 мм² ,
a – 12 мм. В таком случае, получается: sin(α) = 65/12³ = 26,83º.
Острый угол ромба через высоту и сторону
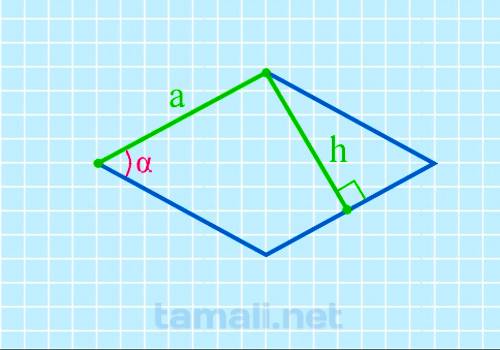
Для определения синуса предполагается использование следующей несложной формулы:
sin(α) = h / a
где h – заявленные показатели высоты, a — сторона.
Цифр после
запятой:
Результат в:
Пример. Допустим, что высота составляет 9, сторона – 15. Следовательно, вычисления
осуществляются следующим образом: sin(α) = 9/15 = 36.86 градусов.
Половинный угол ромба через высоту и диагональ
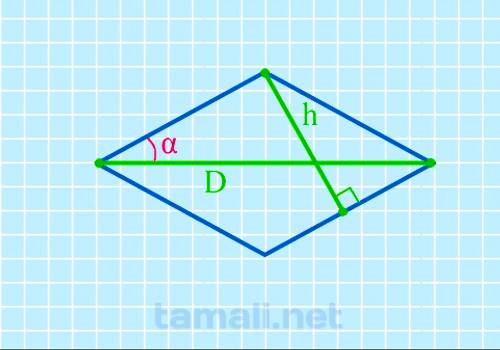
Чтобы отыскать интересующий синус, требуется воспользоваться следующим правилом определения
величины:
sin( α/2 ) = h/D
где h – имеющаяся высота, D – заявленная длина диагонали.
Цифр после
запятой:
Результат в:
Пример. Высота 43, диагональ 76. Следовательно, sin( α/2 ) = 43/76 = 34.4.
Половинный тупой угол ромба через диагонали
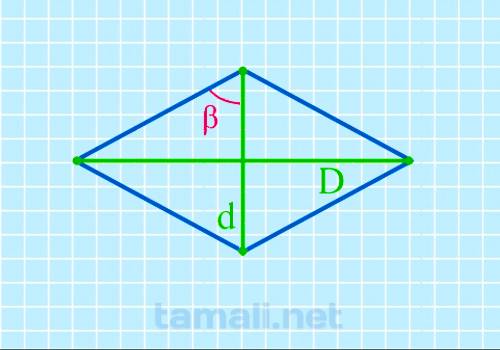
Использование рассматриваемого метода не предполагает под собой существенных сложностей. Достаточно
воспользоваться специально разработанной формулой, которая имеет следующий вид:
tg( β/2 ) = D / d
где D выступает длинной диагональю, d — короткой.
Цифр после
запятой:
Результат в:
Пример. Достаточно подставить для вычисления имеющиеся данные, чтобы в конечном
итоге получить искомый результат. К примеру, D = 80 мм, d = 35 мм. Используя стандартные принципы
вычисления получается: tg( β/2 ) = 80/35 = 66.37
Половинный острый угол ромба через диагонали
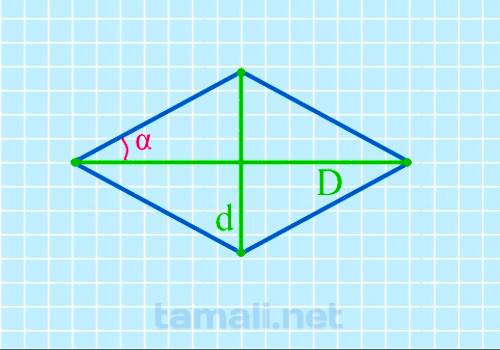
Проведение расчетов с помощью представленной методики требует наличия всех переменных, среди которых
короткая и длинная диагонали. Если все необходимые параметры известны, вычисление осуществляется по
представленной формуле:
tg( α/2 ) = d / D
где D,d – заявленная длина диагоналей.
Цифр после
запятой:
Результат в:
Пример. Предположим, что D = 15 мм, d = 50 мм. Подставим имеющие значения в формулу,
имеем вид: tg( α/2 ) = 50 /15 С помощью несложных подсчетов получается, что tg( α/2 ) = 73.3
градуса.
Ромб представляет собой параллелограмм, который имеем равные стороны. При наличии исключительно
прямых углов – квадрат.
Дополнительно выделяют следующие признаки:
- имеющиеся диагонали ромба перпендикулярны;
- диагонали ромба выступают биссектрисами его углов;
- сумма квадратов всех диагоналей приравнивается к квадраты стороны, которая умножается на 4.
Чтобы параллелограмм считался ромбом, крайне важно соблюдение одного из нескольких условий, к которым
принято относить:
- все имеющиеся стороны геометрической фигуры равны между собой;
- диагонали пересекаются исключительно под прямым углом;
- диагонали геометрической фигуры выступают биссектрисами углов.