Загрузить PDF
Загрузить PDF
У математиков, живших столетия назад, не было транспортиров, с помощью которых можно измерять и строить равные углы. В некоторых случаях на уроках геометрии можно пользоваться только линейкой и циркулем. С помощью этих инструментов можно проводить отрезки определенной длины и рисовать дуги, что позволит построить угол, равный данному.
-
1
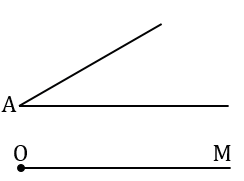
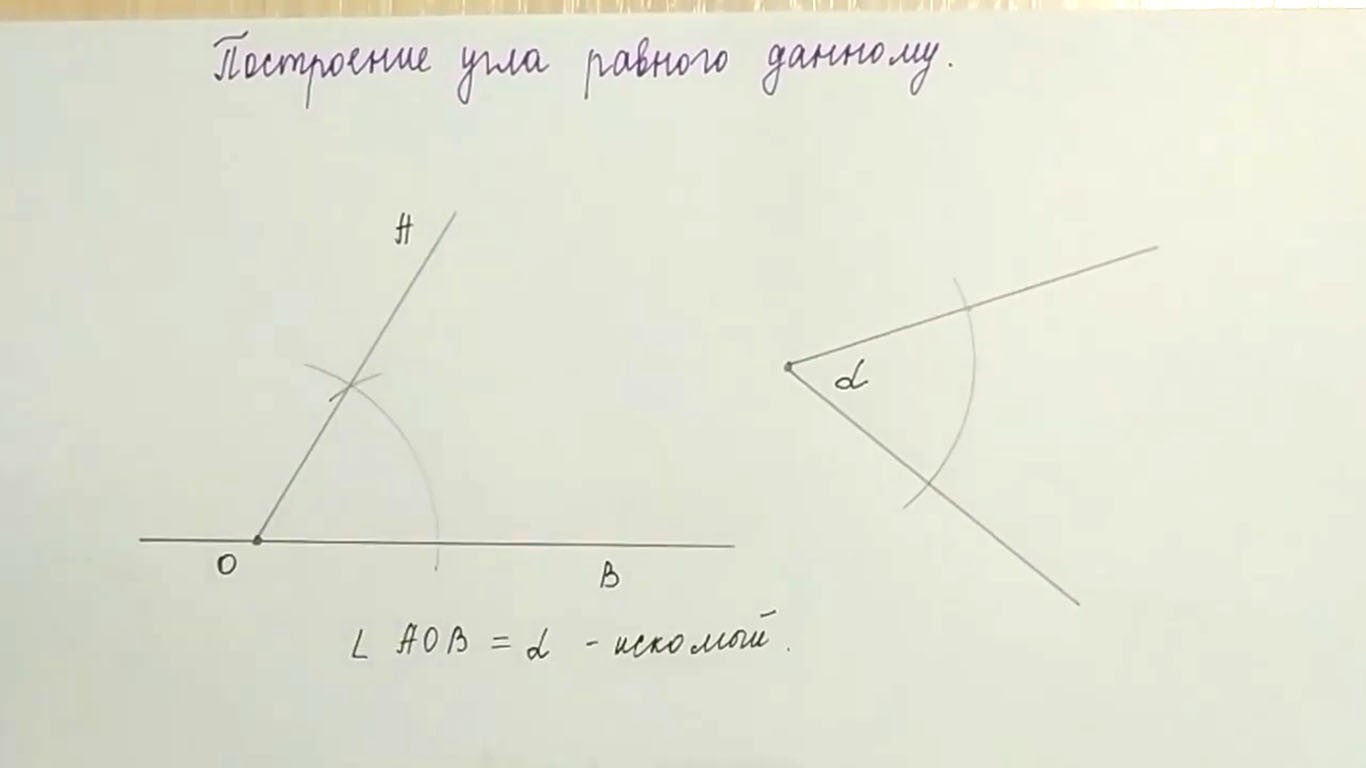
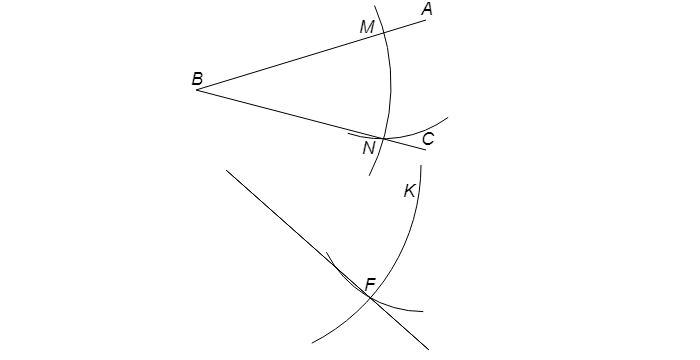
Рассмотрите данный угол. Задача состоит в том, чтобы построить угол, равный данному, используя определенные правила. Сначала рассмотрите данный угол; если нужно, нарисуйте его на бумаге и не забудьте оставить на ней свободное пространство для построения равного угла.
- Данный (исходный) угол обозначьте как ABC. Вершина угла лежит в точке В.
- Угол состоит из двух лучей, которые сходятся в вершине. В нашем примере угол состоит из лучей BA и BC.
-
2
Возьмите циркуль. Это первый инструмент, который необходим для построения равного угла. Циркули бывают разных типов. В дешевые циркули вставляется карандаш, а в более дорогие и точные – специальные сменные грифели. Чтобы построить равный угол, можно воспользоваться любым циркулем.
-
3
Возьмите линейку. Она необходима для проведения прямых линий. На самом деле измерять ничего не нужно, поэтому в качестве линейки можно использовать любой плоский предмет с прямыми сторонами.[1]
-
4
Возьмите карандаш, ручку или любой другой пишущий предмет. Карандаш, вставленный в циркуль, будет использоваться для обозначения отрезков определенной длины, но также понадобится карандаш, ручка или маркер, чтобы проводить прямые линии.[2]
Реклама
-
1
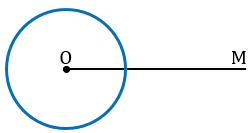
С помощью линейки проведите луч. Сначала поставьте точку М, которая будет обозначать вершину равного угла. От этой точки с помощью линейки проведите прямую линию, длина которой соответствует вашим пожеланиям.[3]
- На конце луча напишите букву N. Таким образом, вы построили луч MN, который является первой стороной равного угла.
-
2
Раствор циркуля сделайте любым. Нужно провести дугу, которая пересечет стороны исходного угла, причем ее радиус не имеет значения. Поэтому раствор циркуля сделайте таким, какой удобен для вас.[4]
-
3
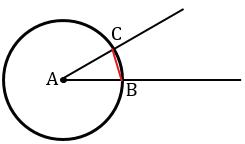
Проведите дугу, которая пересечет обе стороны исходного угла. Постарайтесь пользоваться циркулем так, чтобы его ножки не разъехались. На некоторых циркулях есть специальный винт, который фиксирует заданный раствор. Если такого винта нет, не давите на циркуль, чтобы его ножки не разъехались.[5]
- Поставьте иглу циркуля в точке В (вершина исходного угла) и проведите дугу, которая пересечет лучи BA и BC. Окружность рисовать не нужно.
- Точки пересечения дуги с лучами обозначьте как X и Y.
-
4
Проведите аналогичную дугу, которая пересечет стороны равного угла. Раствор циркуля не меняйте! Поставьте иглу циркуля в точке M и проведите дугу, которая пересечет луч MN, причем длина полученного отрезка будет равна длине соответствующего отрезка исходного угла.[6]
- Точку пересечения дуги с лучом MN обозначьте как F.
-
5
С помощью циркуля измерьте расстояние между точками X и Y. Поставьте иглу циркуля в точке X. Раздвиньте ножки циркуля так, чтобы грифель карандаша совпал с точкой Y. Нарисуйте небольшую дугу, которая пройдет через точку Y.[7]
-
6
Вернитесь к равному углу и отложите расстояние ХY. Раствор циркуля не меняйте! Поставьте иглу циркуля в точке F и проведите дугу, которая пересечет ранее нарисованную дугу. Пересечение двух дуг обозначьте как G.[8]
-
7
С помощью линейки проведите вторую сторону равного угла. Положите линейку так, чтобы совместить ее край с точками M и G. Карандашом или маркером нарисуйте луч, который исходит из точки М и проходит через точку G. На конце луча поставьте букву L. Таким образом, вы построили луч ML.
-
8
Посмотрите на построенный угол LMN. Он равен исходному углу ABC.[9]
- Если построенный угол не равен исходному, во время работы следите за раствором циркуля, который на некоторых этапах менять нельзя.
Реклама
Об этой статье
Эту страницу просматривали 203 732 раза.
Была ли эта статья полезной?
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение угла, равного данному
Пример:
Отложить от данного луча угол, равный данному.
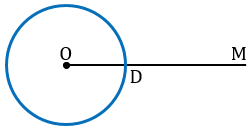
Дано: луч ОМ, 
Отложить: от луча ОМ угол, равный 
Решение:
Произвольно строим с помощью линейки 
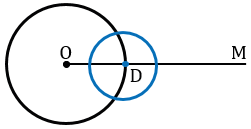
Строим с помощью циркуля окружность произвольного радиуса с центром в вершине 
Точки пересечения окружности со сторонами 
Построим с помощью циркуля окружность того же радиуса, как и окружность с центром в вершине 
Точку пересечения данной окружности с лучом ОМ обозначим D.
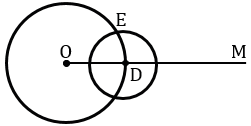
Теперь строим с помощью циркуля окружность радиуса ВС с центром в точке D.
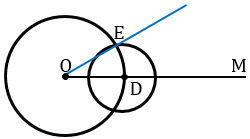
Получаем окружности с центрами в точках О и D пересекаются в двух точках, обозначим одну из этих точек Е.
С помощью линейки проведем луч ОЕ.
Докажем, что 


Рассмотрим треугольники АВС и ОDE.
Отрезки АВ и АС – радиусы окружности с центром в точке А, ОD и ОЕ – радиусы окружности с центром в точке О, а по построению эти окружности имеют одинаковые радиусы, следовательно, АВ = ОD, АС = ОЕ. Также по построению радиус DE окружности с центром в точке D равен отрезку ВС, т.е. DE = ВС. Получаем 








Советуем посмотреть:
Построение биссектрисы угла
Построение перпендикулярных прямых
Построение середины отрезка
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 289,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 361,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 362,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 413,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 586,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 590,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 873,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1181,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В этом материале простое объяснение геометрической задачки, как построить угол, равный данному.
Шаг 1 из 9
Чертим произвольный угол с градусной мерой α.
Шаг 2 из 9
Чтобы построить угол равный данному, проводим прямую и ставим на ней точку. Это будет вершина нашего угла.
Шаг 3 из 9
Берем циркуль с произвольным раствором, ставим его на вершину данного угла.
Проводим дугу таким образом, чтобы она пересекла лучи данного угла.
Шаг 4 из 9
Таким же раствором проводим подобную дугу из вершины нового угла.
Шаг 5 из 9
Дуга будет одинаковой, поэтому будем мерить расстояние между лучами по дуге.
Для этого устанавливаем иглу циркуля в одну точку пересечения луча и дуги и дотягиваемся до другой.
Шаг 6 из 9
Найденное расстояние переносим на новый угол. Не смещая раствор циркуля, устанавливаем его на точку пересечения прямой и дуги и делаем засечку.
Тем самым мы определим точку пересечения со вторым лучом нового угла.
Шаг 7 из 9
Осталось соединить вершину с новой точкой пересечения.
Шаг 8 из 9
Углы будут равными. Проверить это можно с помощью транспортира.
Шаг 9 из 9
Завершаем задачу правильным оформлением. Обозначим лучи и вершину буквами, и напишем ответ.
Download Article
Download Article
Often times, you are required to construct some angles without using a protractor. This article teaches you how to draw a 90 degrees angle using a compass and a ruler.
-
1
Mark the vertex of your angle anywhere on the paper. Let us name this point as M.
-
2
Draw a ray MN, extending in any direction and of any length. This will be one of the arms of our angle.[1]
Advertisement
-
3
Place tip of the compass on point M and draw a circle cutting the ray MN at some point (say P).[2]
-
4
Keep the width of the compass the same. Then place its tip on P and draw an arc cutting the circle at some point (say Q).
-
5
Keep the width of the compass the same. Place its tip on Q and draw another arc cutting the circle at another point (say R).[3]
-
6
Keep the tip of the compass still on Q. Draw another arc somewhere outside the circle. For carrying out this step, you can set the width of the compass to any measure.[4]
-
7
Keep the same width of the compass (as set in the previous step). Now place its tip on R and draw another arc which cuts the arc drawn in the previous step at some point (say S).
-
8
Connect the points M and S with a straight line. Extend it to form a ray ML.[5]
- The measure of the angle LMN is 90O.
Advertisement
-
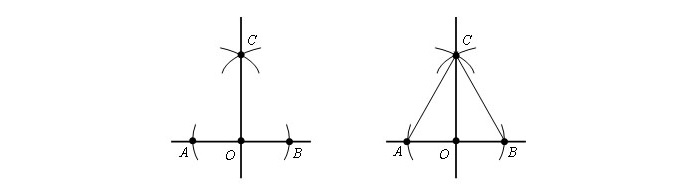
1
Draw a straight line. On a piece of paper, draw a line segment of any convenient length. Make it horizontal for the sake of simplicity, but it could be at any angle. Label the line segment AB.[6]
-
2
Pick any point on AB. Mark it, and label it O. O can be anywhere on the line segment, including at either end point (A or B). For convenience, let’s put O somewhere near the middle of AB. The line segment could now be referred to as AOB.
-
3
Grab a compass. Open the compass to a radius a little shorter than either AO or OB. Now place the compass point at O. Strike short arcs through AB on either side of O. The two arcs should have the same radius. Label those two points of intersection C and D. Now the line segment could be referred to as ACODB.[7]
-
4
Strike two more arcs. Place the compass point at C, and strike an arc to one side of the line segment. Then place the compass point at D, and strike a second arc of the same radius and on the same side of the line segment. Make sure those two arcs intersect. Call that point of intersection E.[8]
-
5
Draw the 90° angle. Draw a straight line from E to O. Line segment EO forms a 90° angle with line segment AB. It actually forms two 90° angles at O. If you were to extend EO beyond AB, you would form four 90° angles at O.[9]
- Note that you can draw a 90° angle at either end of line segment AB if you want to (in other words at point A or point B). Simply extend AB beyond A or beyond B, and then follow the above steps. Point A (or point B) would serve as point O in the above instructions.
- This is essentially the same method featured in How to Construct a Perpendicular Line to a Given Line Through Point on the Line, Method 2.
Advertisement
Add New Question
-
Question
How do I draw a right angle triangle?
First construct a 90° angle as shown above. Extend each leg of the angle any convenient length. Draw a line from the end of one leg to the end of the other. You have a right triangle.
-
Question
How do I construct a 15 degree angle?
First, make a 60 degree angle by constructing an equilateral triangle. Use angle bisection construction to make a 30 degree angle. Bisect the 30 degree angle again to make a 15 degree angle.
-
Question
Can I draw a 133-degree angle?
There is no way to construct such an angle using a compass and a ruler. That’s why they invented the protractor.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Paper
- Pen or pencil
- Ruler or another straightedge
- Compass
References
About This Article
Thanks to all authors for creating a page that has been read 112,731 times.
Reader Success Stories
-
Payal Sharma
Sep 27, 2016
“A really detailed and elaborate answer! Keep it going! Better than my maths teacher!”
Did this article help you?
Как построить угол равный данному с помощью циркуля и линейки
В этом материале простое объяснение геометрической задачки, как построить угол, равный данному.
Чертим произвольный угол с градусной мерой α.
Чтобы построить угол равный данному, проводим прямую и ставим на ней точку. Это будет вершина нашего угла.
Берем циркуль с произвольным раствором, ставим его на вершину данного угла.
Проводим дугу таким образом, чтобы она пересекла лучи данного угла.
Таким же раствором проводим подобную дугу из вершины нового угла.
Дуга будет одинаковой, поэтому будем мерить расстояние между лучами по дуге.
Для этого устанавливаем иглу циркуля в одну точку пересечения луча и дуги и дотягиваемся до другой.
Найденное расстояние переносим на новый угол. Не смещая раствор циркуля, устанавливаем его на точку пересечения прямой и дуги и делаем засечку.
Тем самым мы определим точку пересечения со вторым лучом нового угла.
Осталось соединить вершину с новой точкой пересечения.
Углы будут равными. Проверить это можно с помощью транспортира.
Завершаем задачу правильным оформлением. Обозначим лучи и вершину буквами, и напишем ответ.
Построение с помощью циркуля и линейки – описание, алгоритмы и задачи
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
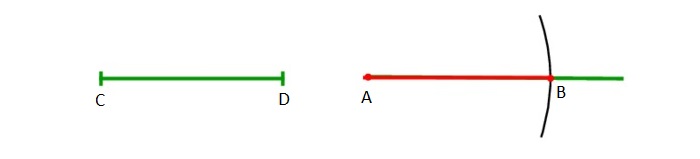
Построение отрезка, равного данному
Есть отрезок СD. Задача – начертить равнозначный данному отрезок той же величины.
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
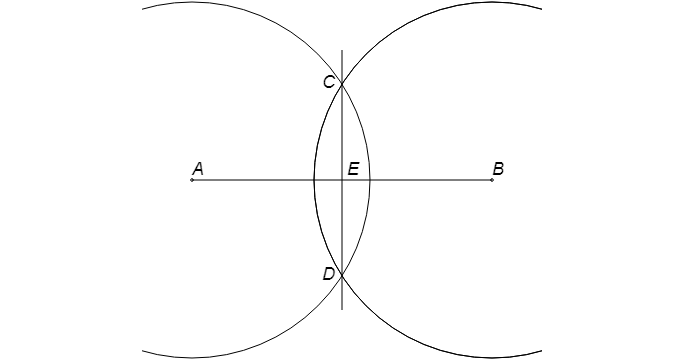
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
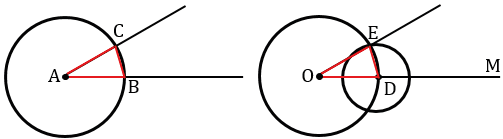
Построение угла, равного данному
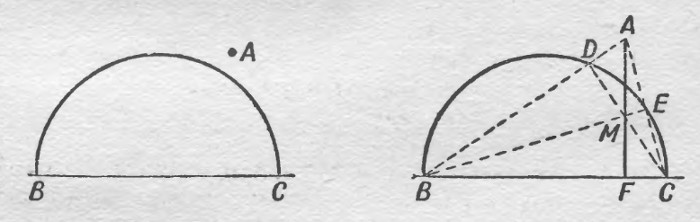
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка – AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 – место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
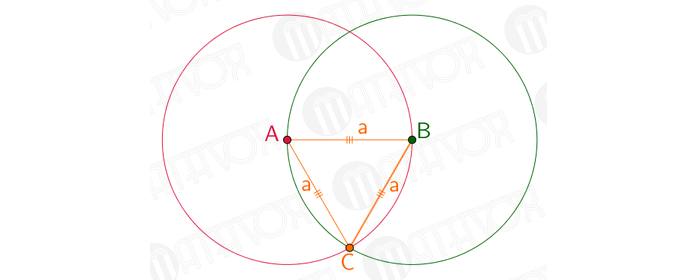
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
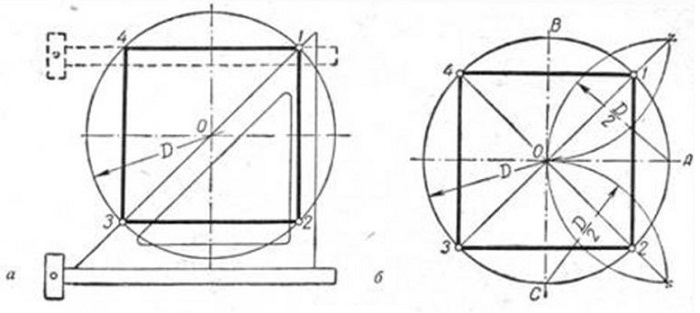
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
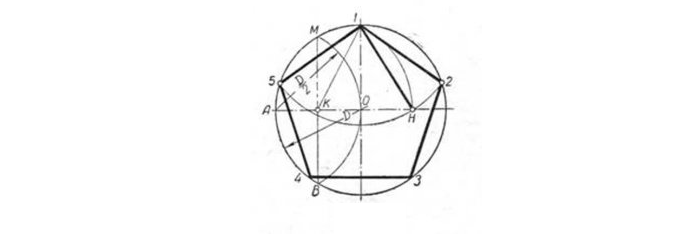
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
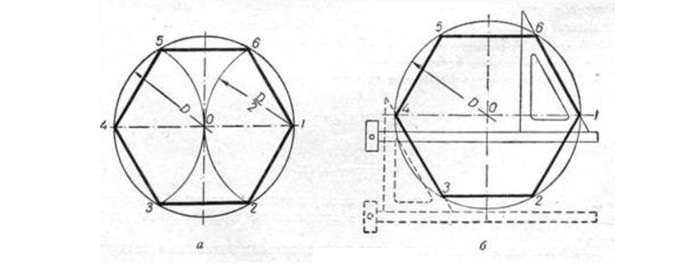
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
На данной ограниченной прямой построить равносторонний треугольник
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
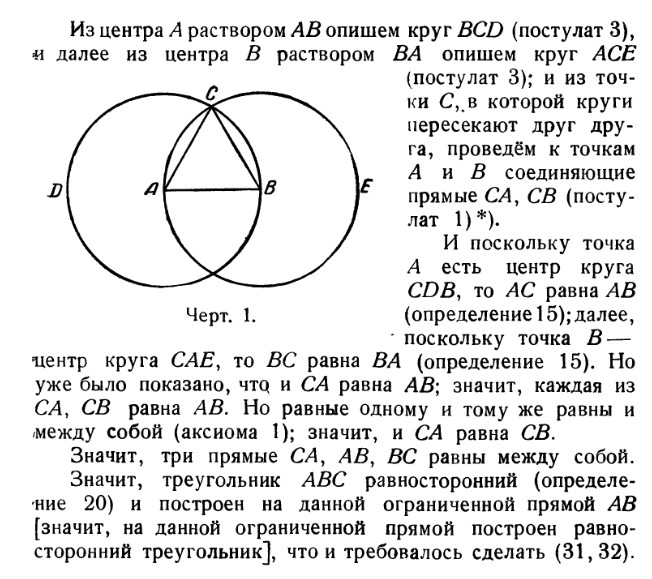
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
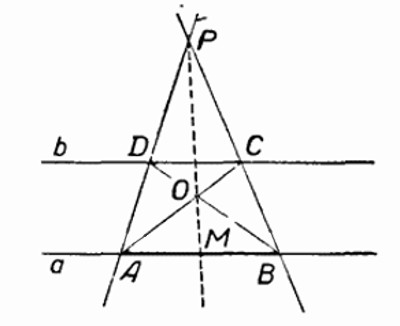
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
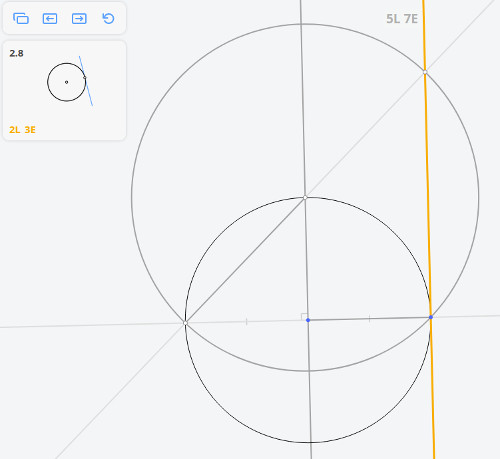
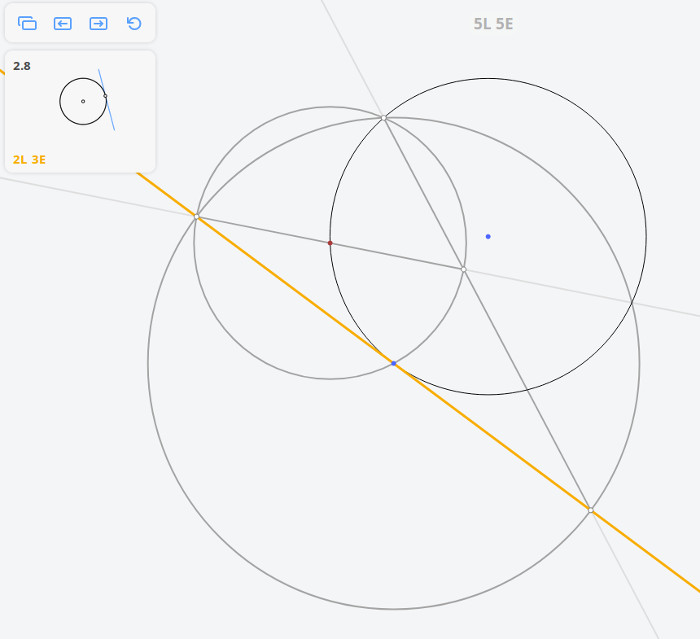
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
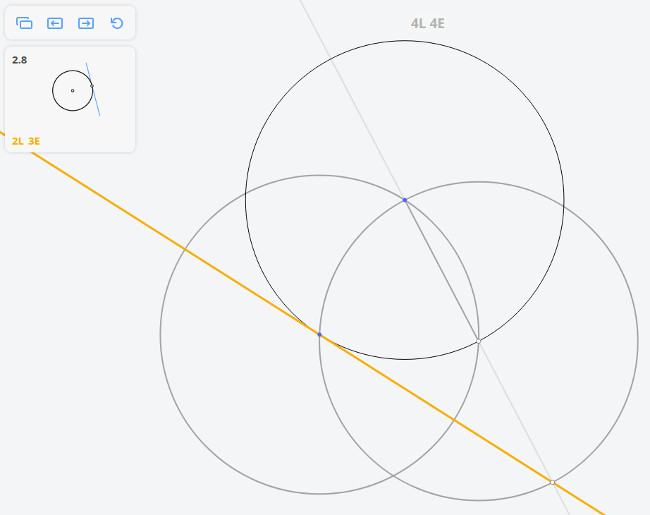
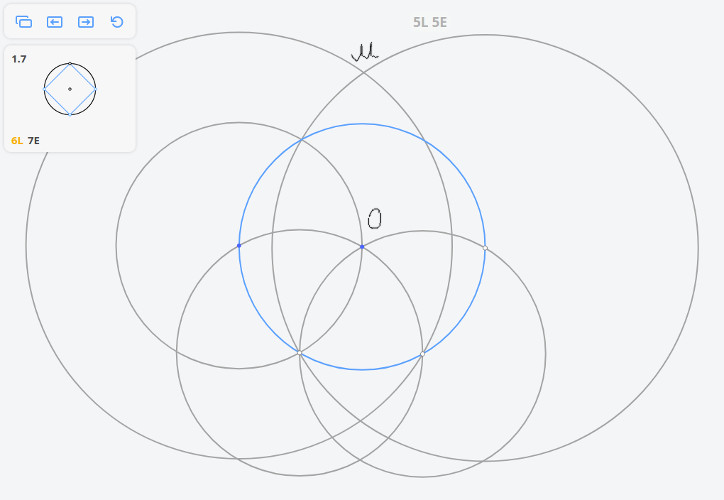
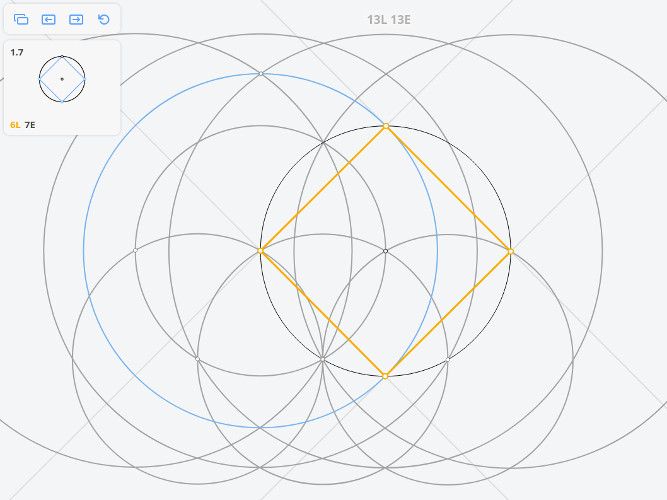
1.7 Квадрат, вписанный в окружность
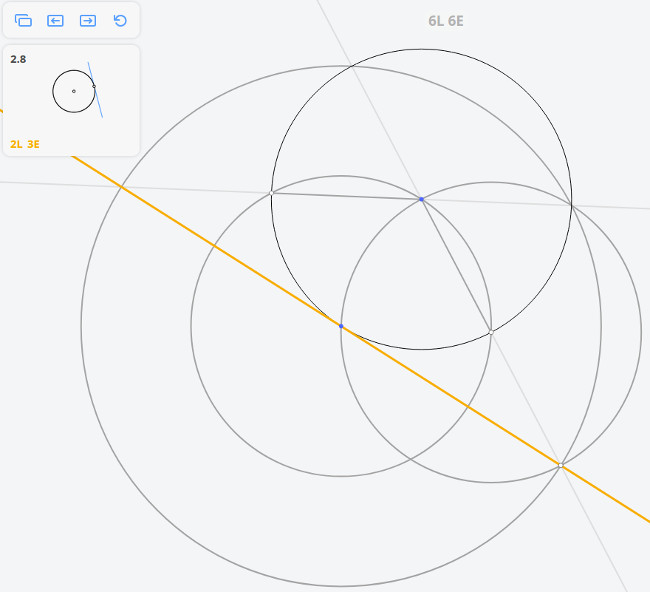
Задача Наполеона
Решим задачу методом Мора-Маскерони.
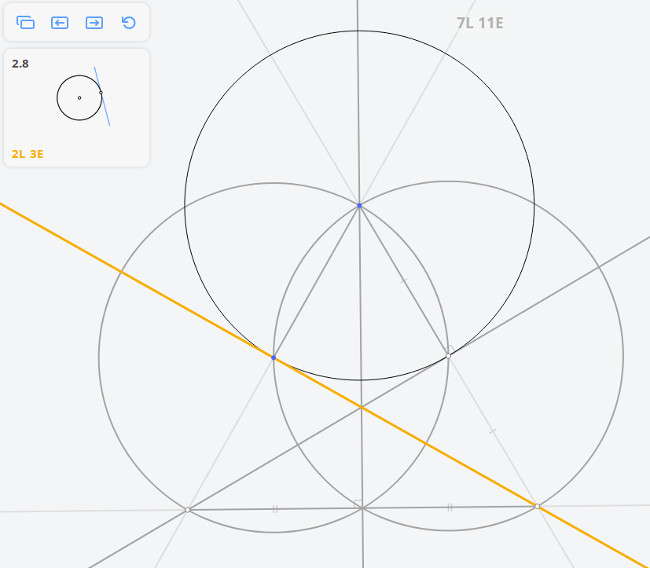
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
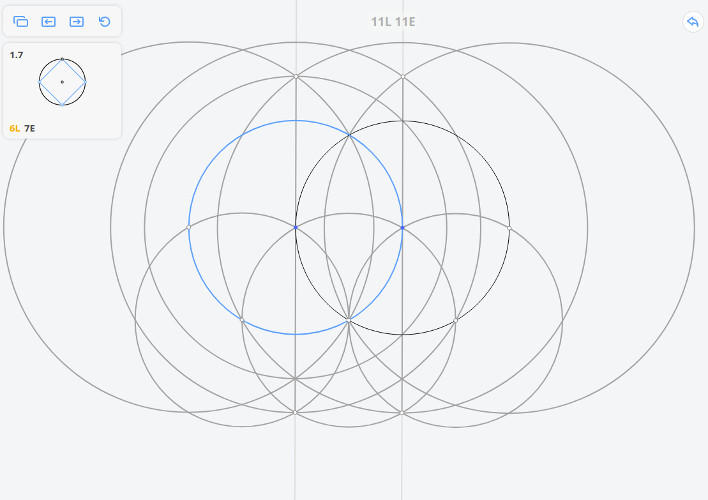
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/postroenie-s-pomoshchyu-tsirkulya-i-lineyki.html
http://habr.com/ru/post/478410/
[/spoiler]