Сдвиг фаз между током и напряжением в цепи переменного тока
Содержание
- 1 Определения и основные формулы
- 2 ПТ и активная нагрузка
- 3 Конденсатор в цепи ПТ
- 4 Индуктивность в цепи ПТ
- 5 Видео по теме
При транспортировке электрической энергии от мест её генерации (тепловые, атомные и гидроэлектростанции) до конечных потребителей необходимо неоднократно варьировать величину напряжения (понижать или повышать). С наибольшей эффективностью эти преобразования удаётся сделать, когда в линиях электропередачи используется переменное напряжение. При этом электрический ток, возникающий в результате действия переменного электрического поля, будет также переменным, изменяясь во времени периодически с такой же частотой. Если в сети присутствуют реактивные элементы (ёмкости, индуктивности), то возникает сдвиг фаз между переменным током и напряжением.
Определения и основные формулы
Переменным принято называть ток, изменяющийся с течением времени как по величине, так и по амплитуде. В английской технической литературе используется термин alternating current (AC). Он переводится как «чередующийся ток» или ток, изменяющий свою полярность.

Периодический переменный ток (ПТ) — это ток, который через идентичные интервалы времени принимает исходную величину, совершая таким образом циклический процесс, аналогичный гармоническому колебанию маятника. Гармонические колебания описываются с помощью синусоидальной функции:

Величина, которая определяется как произведение ω на t и имеет размерность угла (в радианах угол 90 градусов соответствует π/2 радиан), называется фазой синусоидальной переменной. В данном случае тока. Формула справедлива для случая, когда измерение тока стартует с точки отсчёта t = 0. В общем случае рабочая формула выглядит так:

Используя специальный измерительный прибор — осциллограф, можно наблюдать синусоиду напряжения на экране и определять её параметры.

ПТ и активная нагрузка
Если к источнику переменного тока подключено обычное сопротивление (резистор), то согласно закону Ома ток на резисторе, равен:

В приведенной выше формуле величина I0 = U0 / R — амплитуда ПТ. Видно, что ток в цепи с активным сопротивлением изменяется с течением времени абсолютно синхронно с напряжением.

Таким образом, на активной нагрузке угол сдвига фаз между током и напряжением равен нулю.
Конденсатор в цепи ПТ
Конструкция конденсатора препятствует протеканию постоянного тока, полностью его блокируя. Поочерёдно заряжаясь и разряжаясь конденсаторные пластины поддерживают ток в цепи, поскольку по определению ток I — это изменение заряда Q за единицу времени:

Ниже представлена картинка, объясняющая подключение конденсатора С к источнику переменного напряжения U.

Напряжение на конденсаторе в любой момент времени равно напряжению:

Тогда заряд Q(t) на обкладках конденсатора определим, используя выражение:

Пользуясь формулой для тока, получим первую производную от заряда по времени, которая равна ёмкостному току Ic(t):

Из графиков, представленных на картинке ниже, видно, что максимальная амплитуда тока наступает на четверть периода раньше, чем напряжения. Из этого следует, что фаза напряжения на π/2 радиан меньше фазы электротока. То есть, в цепи синусоидального тока существует отставание напряжения по фазе (фазовый сдвиг) на π/2.

Данное явление может быть объяснено по-другому. Из курса тригонометрии известно, что:

С помощью формул, приведенных выше, можно получить такое выражение:

Данное соотношение в явном виде показывает, что фазовый сдвиг равен π/2.
Индуктивность в цепи ПТ
Катушка индуктивности в цепях СПТ является реактивным элементом, поскольку ее активное сопротивление практически равно нулю. При подключении катушки также возникает фазовый сдвиг, но его причина несколько иная, чем в цепи с емкостью.

При практически нулевом омическом сопротивлении не может возникнуть короткое замыкание (резкий рост тока), поскольку переменный характер напряжения включает иной механизм сопротивления. Согласно закону, открытому британским учёным Майклом Фарадеем, в катушке появляется переменное магнитное поле, которое создает магнитный поток F, инициирующий появление электродвижущей силы (ЭДС самоиндукции) на концах катушки индуктивности:

В соответствии с законом Фарадея:

Откуда следует, что:

Используя данную формулу, находим определение для тока на индуктивности:

Как известно,

Следовательно, в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен π/2, причём ток отстаёт по фазе от напряжения.

Из графика видно, что максимум силы тока достигается на четверть периода позже, чем максимум напряжения, что соответствует отставанию по фазе на π/2.
От угла сдвига фаз зависит, какова будет реактивная мощность и, следовательно, коэффициент мощности, который выражается через cosφ и является очень важной характеристикой для оценки эффективности работы электрооборудования. Его значение может находиться в диапазоне от нуля до единицы. Если cosφ = 0, это означает, что в электроцепи присутствуют лишь реактивные токи. На практике такая ситуация невозможна, но чтобы потери мощности, связанные с реактивными токами, были меньше, используют компенсационные устройства.
Принцип действия таких устройств основывается на свойстве конденсаторов и катушек сдвигать фазу в противоположных направлениях. Компенсаторы зачастую используют в производственных цехах, где работает большое количество электрооборудования. Это приводит к ощутимым потерям электроэнергии и ухудшению качества электротока. Устройство компенсации решает подобные проблемы. Им успешно силу тока изменяют, если что-то сдвигают. Обычно такое устройство состоит из блоков конденсаторов довольно большой емкости, которые помещаются в отдельных шкафах.
Видео по теме
Угол сдвига фаз
Это разность
начальных фаз двух переменных.
![]()
1 Та переменная,
которая раньше достигает положительного
максимума опережает по фазе, которая
позже отстает по фазе
![]() –
–
опережает по фазе,![]() -отстает
-отстает
по фазе.

2 Если две переменные
одновременно проходят максимум и ноль,
то они совпадают по фазе.

Если угол сдвига
фаз равен 1800,
то переменные проходят в противофазе.

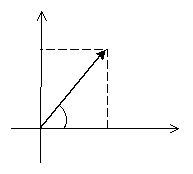
Временная и векторная диаграммы
Временная
диаграмма–
это зависимость переменной от времени
t
или от угла
![]() ,
,
если начальная фаза положительна, то
она откладывается влево от начала
координат, ели отрицательна- вправо.
Построим временную
диаграмму для двух переменных
![]()
![]()
Временная диаграмма

Угол сдвига фаз
равен
![]()
Любую синусоиду
можно изобразить вектором. Длина,
которого равна максимальному или
действующему значению и расположен он
под углом, равным начальной фазе к
положительному направлению горизонтальной
оси. Если начальная фаза положительна
она откладывается вверх, если отрицательна
– вниз.

Действующие
значения переменных
![]()
![]()
Угол между векторами
равен углу сдвига фаз между ними.
Тестовые задания:
|
Задание |
Временные |
Варианты |
|
3.Укажите |
|
а) U1
б) U1
в) U1 г) |
|
Задание |
Варианты |
|
|
1.Характеризует |
Да; Нет. |
|
|
Задание |
Математические |
Варианты |
|
2.Укажите |
а) в) |
1) угловая частота;
2) циклическая
3) угол сдвига |
Комплексные числа в применении к электрическим цепям
![]()
 -комплексное
-комплексное
обозначение электрических величин. В
некоторых учебниках (![]() )
)
![]() –
–
алгебраическая форма комплексного
числа
![]() –
–
показательная форма комплексного числа
Изобразим комплексное
число вектором ОМ.
Перевод комплексных
чисел из одной формы в другую осуществляется
следующим образом:
Дано число в
алгебраической форме
![]() .
.
Чтобы перевести его в показательную
форму используем выражения![]() и
и![]() .
.
Если мнимая часть «b»
отрицательна то угол «![]() »
»
также отрицательна.
Дано число в
показательной форме
![]() Чтобы перевести его в алгебраическую
Чтобы перевести его в алгебраическую
форму используем выражения![]() и
и![]() .
.
Если угол![]() отрицательный, то и мнимая часть будет
отрицательный, то и мнимая часть будет
отрицательной.
Пример перевода
комплексных чисел.
1)
![]()
![]()
![]()
2)
![]()
![]()
![]()
3)
![]()
![]()
![]()
Чтобы записать
ток в комплексной форме используют
показательную форму записи комплексных
чисел: модуль равен максимальному или
действующему значению, а аргумент
начальной фазе.
![]()
![]()
![]()
![]()
![]()
![]()
Например:
![]()
![]()
![]()
Запишем законы
Ома и Кирхгофа в комплексной форме
Первый закон
Кирхгофа:
![]()
Второй закон
Кирхгофа:
![]()
Цепь с резистором при гармоническом воздействии

Приложим к резистору
переменное напряжение
![]() .
.
По закону Ома для мгновенных значений
получим![]()
Вывод: в цепи с
резистором напряжение и ток совпадают
по фазе
![]()

![]()
Временная диаграмма
для
цепи с резистором.
Векторная диаграмма
для цепи
с резистором.
Угол сдвига фаз между током и напряжением

Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0 о до 360 о в некоторых случаях от -180 о С до +180 о С, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.

Рис. 2. коэффициент мощности
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Реактивная составляющая
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Рис. 3. Устройство компенсации
Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Рис. 4. Компенсация реактивной мощности с помощью конденсаторов
Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5 о . Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).

Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.

Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Источник
Измерение фазового сдвига
Фазовый сдвиг
Фазовым сдвигом называется модуль разности начальных фаз двух гармонических сигналов одной частоты и . Таким образом фазовый сдвиг равен . Он является постоянной величиной и не зависит от момента отсчёта.
Фазовый сдвиг можно выразить через разность моментов времени , в которых эти колебания имеют одинаковые фазы (рис. 11.1 а) рис. 11.1
Это определение распространяется на два периодических сигнала несинусоидальной формы (рис.11.1 б), если в момент перехода через ноль их напряжения изменяются в одну сторону (например, от положительных значений к отрицательным).

Рис. 11.1.
Необходимость измерения фазового сдвига возникает при исследованиях фазочастотных характеристик радиотехнических устройств, измерениях реактивной мощности, оценке свойств веществ.
Приборы для измерения разности фаз называют фазометрами или измерителями фазового сдвига и согласно ГОСТ15094 подразделяются на:
- Ф1 – установки и приборы для поверки измерителей фаз;
- Ф2 – измерители фаз;
- Ф3 – фазовращатели измерительные;
- Ф4 – измерители группового времени запаздывания.
Методы измерения фазового сдвига весьма разнообразны и зависят от диапазона частот, требуемой точности и от формы исследуемых сигналов. На практике нашли применение следующие методы:
- осциллографический;
- компенсационный;
- дискретного счета.
Осциллографический метод
Этот метод реализуется с помощью линейной, синусоидальной и круговой разверток.
Метод линейной развертки
Для этого используется двухлучевой или двухканальный осциллограф. На входы Y1 и Y2 подаются исследуемые сигналы. Частота развертки подбирается так, чтобы на экране наблюдалось 1-2 периода сигналов (рис.11.1 а). Измерив Т и по формуле определяют фазовый сдвиг, где ab и ac – измеренные на экране ЭЛТ длины отрезков.
Метод синусоидальной развертки
Метод может быть реализован с помощью однолучевого осциллографа. Один сигнал подается в канал Y, а второй – на канал Х (генератор развертки отключен). На экране осциллографа получается эллипс (рис. 11.2 рис. 11.2.), уравнение которого
где a, b – максимальные отклонения по горизонтали и вертикали соответственно.
Рис. 11.2.
Существует ряд методов определения фазового сдвига по полученной фигуре.
Метод 1.
Положив x=0 получим вертикальный отрезок . Если y=0, то горизонтальный отрезок . Следовательно , откуда можно определить
Метод неточен из-за трудности определения центра эллипса, но зато полученные формулы не зависят от соотношений Ux и Uy.
Метод 2.
Реализуется при условии a=b. В этом случае , где l1 — малая ось эллипса, l2 — его большая ось.
Метод 3.
При любых значениях a и b , где определяются по экрану ЭЛТ осциллографа.
Осциллографический метод прост, не требует дополнительных приборов, но не даёт однозначности (знак угла) и обладает большой субъективной погрешностью. Погрешность определения фазового сдвига составляет 5-10% из-за неточностей определения длин отрезков, искажений эллипса.
Метод круговой развертки
При использовании этого метода опорное напряжение с помощью фазовращателя ФВ расщепляется по фазе и в виде двух сдвинутых на 90o напряжений подается на вход усилителей У1 и У2 каналов X и Y (рис.11.3). Регулировкой коэффициентов усиления и установлением фазовой симметрии в обоих каналах добиваются получения круговой развертки.

Рис. 11.3.
Метод круговой развертки
Напряжение исследуемого сигнала подается на модулирующий электрод ЭЛТ (канал Z). На время отрицательного полупериода ЭЛТ запирается и на экране становится видимой только половина окружности. Для обеспечения необходимой точности измерений необходимо, чтобы трубка запиралась в моменты перехода сигнала через ноль, что обеспечивается применением усилителя-ограничителя УО.
В процессе измерения фазового сдвига на вход УО сначала подается опорное напряжение (положение 1) и по полуокружности на экране ЭЛТ отмечается положение диаметра mn, являющегося началом отсчета. Затем на УО подается измеряемый сигнал (положение 2) и отмечается положение pq. Измеряемый фазовый угол равен углу между прямыми mn и pq.
Источниками погрешности являются: непостоянство частоты круговой развертки, погрешность измерения угла между диаметрами, погрешность УО.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:
- электрочайник (Pf = 1);
- лампы накаливания (Pf = 1);
- электроплита (Pf = 1) и другие нагревательные приборы;
Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.

Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0о до 360о в некоторых случаях от -180оС до +180оС, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Как измеряется угол сдвига фаз осциллографом
Осциллографический способ можно отнести к самому простейшему с погрешностью в районе 5о. Определение сдвига осуществляется при помощи осциллограмм. Существует четыре осциллографических метода:
- Применение линейной развертки.
- Метод эллипса.
- Метод круговой развертки.
- Использование яркостных меток.
Определение угла сдвига фаз зависит от характера нагрузки. При определении фазного сдвига в первичной и вторичной цепях трансформатора, углы могут считаться равными и практически не отличаются друг от друга.
Угол сдвига фаз напряжений, измеряемый по эталонному источнику частоты и при использовании измерительного органа лает возможность обеспечить точность всех последующих измерений. Фазные напряжения и угол сдвига фаз зависят от нагрузки, так симметричная нагрузка обуславливает равенство фазного напряжения , токов нагрузки и угол фазного сдвига, также будет равна нагрузка по потребляемой мощности на всех фазах электроустановки.
Угол сдвига фаз между током и напряжением в несимметричных трехфазных цепях не равны друг другу. Для того чтобы вычислить угол сдвига фаз (угол φ) в цепь включают последовательно присоединенные сопротивления (резисторы), индуктивности и конденсаторы (емкости).
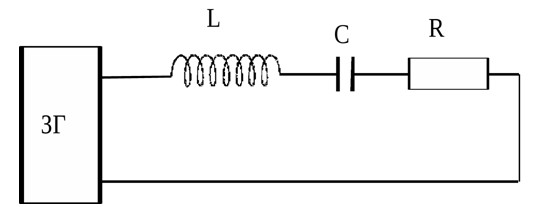
Рис. №1. Последовательное соединение сопротивления, индуктивности и емкости для вычисления угла сдвига фаз. В этом контуре протекает переменный ток, который способствует возникновению ЭДС.

Рис. №2. Схема проведения опыта по определению сдвига фаз между током и напряжением. Слева показаны схемы подключения конденсаторов, катушек индуктивности и резисторов, справа показаны результаты опыта.
Из результатов опыта можно определить, что сдвиг фаз между напряжением и током служит при определении нагрузки и не может зависеть от переменных величины тока и напряжения в электрической сети.
Как вывод, можно сказать, что:
- Составляющие элементы комплексного сопротивления, такие как резистор и емкость, а также проводимость не будут взаимообратными величинами.
- Отсутствие одного из элементов делает резистивные и реактивные значения, которые входят в состав комплексного сопротивления и проводимости и делают их величинами взаимообратными.
- Реактивные величины в комплексном сопротивлении и проводимости используются с противоположным знаком.
Угол сдвига фаз между напряжением и током всегда выражается, как главный аргументированный фактор комплексного сопротивления φ.
Дорогие друзья! Здравствуйте! Хочу рассказать, как же связаны между собой напряжения в трёхфазной сети в независимости какое в ней напряжение и частота. От напряжения и частоты и мощности зависят только габариты генераторов и промежуточных трансформаторов, но об этом можно побеседовать в другой публикации…
Как устроен трёхфазный генератор знают все – по кругу в статоре расположены три обмотки. И как Вы правильно заметили расположены они через 120 угловых градусов. Внутри ротора вращается роторная обмотка, образующая постоянное магнитное поле. Можно вместо обмотки вращать постоянный магнит, но возникает проблема регулировки выходного напряжения и это можно сделать только при помощи катушки, выводы которой через вращающиеся кольца подключены к регулятору, отвечающему за величину выходного генератора. А чтобы выходная частота генератора была равна 50 Гц – ротор должен вращаться со скоростью 3000 оборотов в минуту если в статоре стоят однополюсные обмотки или 1500 оборотов в минуту если обмотки двухполюсные, второй вариант предпочтительнее, так частота вращения ниже, что очень важно для механики.
Теперь и о самом угле между напряжениями: расположение обмоток и определяет угол сдвига и он, естественно, равен 120 градусов и даже думать не надо, 120 градусов и всё точка!!!
Но оказывается, что иногда для измерений или питания нестандартных устройств требуется угол отличный от 120 градусов, но четко привязанный к одной из фаз.
При одном из вариантов схемного решения устройства контроля потребовалось измерять амплитуду линейного напряжения между фазами «А» и «С» и через определенное время амплитуду между фазами «В» и «С». И как н странно контроллер через 120 градусов не обнаружил напряжения. Ошибка в схеме? Нет! Ошибка ( а может геометрию забыл) в программе! Оказалось, что амплитуду надо ожидать не через 120 градусов, а через 60!!! Перепрошил контроллер и все заработало. Между линейными напряжениями угол 60 градусов! На треугольнике это очень хорошо видно.
А как быть если нужен сдвиг 90 градусов? Задача решается при помощи трансформатора или дросселя с симметричным выводом от средней точки обмотки.
Мощность потребителя, подключаемого к точкам «A» – «D» должна соответствовать допустимой мощности дросселя или резисторам в сдвигающей цепочке.
Надеюсь, что эта информация полезна и кто-то применит её в своих конструкциях, А я в ближайшее время приведу схему конструкции, контролирующей качество трёхфазной сети, питающей ответственных потребителей.
Желаю всем успехов в творчестве!!! Здоровья в теле!!! И счастья в жизни!!! Берегите себя в столь трудное время!!!

