
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
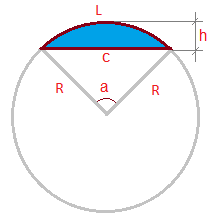
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
![]()
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
![]()
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
![]()
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
![]()
Круговой сегмент – все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Длина дуги сегмента круга рассчитывается также как и длина дуги сектора – умножением радиуса на центральный угол сектора:
P=αr
Если провести из центра окружности перпендикуляр к хорде, то мы получим прямоугольный треугольник внутри равнобедренного, образованного радиусами. Половина хорды в таком треугольнике является катетом, противолежащим половинному углу α. Зная радиус, можем найти хорду через синус половинного угла. (рис. 141)
c/2=r sin〖α/2〗
c=2r sin〖α/2〗
Высота сегмента круга равна разности радиуса и высоты равнобедренного треугольника, являющейся также катетом прямоугольного треугольника. Так как катет, выраженный через радиус, равен косинусу половинного угла, то найти высоту сегмента можно по следующей формуле. (рис.142)
h=r-H=r-r cos〖α/2〗=r(1-cos〖α/2〗 )
Площадь сегмента круга всегда равна разности площади сектора круга и площади равнобедренного треугольника, образованного радиусами и хордой. Так как площадь сектора круга равна полупроизведению квадрата радиуса на центральный угол, а площадь равнобедренного треугольника равна половине квадрата стороны, то есть радиуса, умноженной на синус угла между ними, то формула площади сегмента круга получает следующий вид.
S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
Информация по назначению калькулятора
Сегмент круга – это область, ограниченная дугой и хордой этого круга. Когда что-то делится на части, каждая часть называется сегментом. Точно так же сегмент является частью окружности. Но сегмент – это не какая-то случайная часть окружности, это определенная часть окружности, которая разрезана ее хордой.
Дуга – это часть окружности круга. Хорда – это отрезок прямой, соединяющий любые две точки на окружности круга.
Существует два типа сегментов: один – второстепенный сегмент, а другой – основной сегмент. Второстепенный сегмент образован малой дугой, а основной сегмент образован большой дугой окружности.
Далее представлены свойства сегмента круга:
⇒ Это область, которая окружена хордой и дугой.
⇒ Угол, уменьшенный на отрезок в центре окружности, совпадает с углом, уменьшенным на соответствующую дугу. Этот угол обычно известен как центральный угол.
⇒ Меньший сегмент получается путем удаления соответствующего большого сегмента из общей площади круга.
⇒ Большой сегмент получается путем удаления соответствующего меньшего сегмента из общей площади окружности.
⇒ Полукруг – это самый большой сегмент в любом круге, образованном диаметром и соответствующей дугой.
Онлайн калькулятор предназначен для нахождения параметров сегмента круга, таких как:
- Площадь
- Длина хорды
- Высота
- Длина дуги
- Периметр сегмента
- Центральный угол сегмента в градусах и радианах
– дуга и два радиуса окружности образуют сектор. Эти два радиуса и хорда сегмента вместе образуют треугольник. Таким образом, площадь сегмента окружности получается путем вычитания площади треугольника из площади сектора.
– находится через радиус и угол между радиусами (c = 2r * sin(α / 2))
– можно найти зная радиус и длину хорды (h = r – √(r2 – c2 / 4))
– находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)
– равен сумме длины дуги и длины хорды (Ps = L + c)
Сегмент круга
Данный калькулятор считает параметры сегмента круга, а именно:
- длину дуги (L),
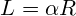
- длину хорды (C),
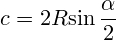
- площадь (S),
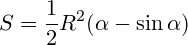
- высоту (h),
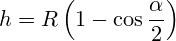
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Однако, как справедливо заметил наш пользователь:“на практике hourто случается, что как радиус дуги, так и угол неизвестны” (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Расчет на круговом сегменте. Круговой сегмент образован окружностью и одной из ее хорд. Введите значения радиуса окружности, высоты отрезка и его угла. Углы рассчитываются и отображаются в градусах.
.
Поделиться расчетом:
Круговой сегмент
Радиус(r)
Высота(h)
Угол(α)
Длина дуги(l)
Длина хорды(m)
Периметр(P)
Площадь(S)
Вычислить
Очистить
Формулы
 α = 2 * arccos ( 1 — h / r )
α = 2 * arccos ( 1 — h / r )
h = r * ( 1 — cos(α/2) )
l = r * α
m = 2 * √2 * r * h — h2
p = l + m
S = r * l / 2 — m * ( r — h ) / 2
