Как найти угол склонения звезды - Сайт, где вы сможете решить свои вопросы

Содержание

Как найти склонение звезды формула астрономия
Формула для вычисления склонения звезды
Как использовать склонение звезды
Итог
Как найти склонение звезды формула астрономия
Что такое склонение звезды?
Формула астрономии для нахождения склонения звезды
Шаги для использования формулы астрономии
Общий итог
Как найти склонение звезды
Используйте формулу для вычисления склонения
Как использовать формулу
Проверьте свои результаты
Заключение

Как найти склонение звезды формула астрономия

Астрономы изучают звезды уже много лет. Одним из методов, который они используют, является определение склонения звезды. Склонение звезды — это угол между плоскостью экватора и звездным меридианом точки, находящейся под звездой. Он обычно измеряется в градусах, минутах и секундах тропического года, и может использоваться для определения многих характеристик звезды, таких как ее положение на небе и ее движение.

Формула для вычисления склонения звезды

Формула для вычисления склонения звезды включает в себя несколько компонентов:

Склонение звезды = 180° — A — B

Где A — прямое восхождение звезды, а B — звездное время.

Прямое восхождение звезды — это аналог долготы звезды на небесной сфере. Он измеряется в часах, минутах и секундах прав ascension (RA). Звездное время — это угловое расстояние между точкой весеннего равноденствия и солнцем, которое измеряется в часах, минутах и секундах правого восхождения.

Чтобы вычислить склонение звезды, нужно сначала определить значения A и B, а затем использовать формулу. Это можно сделать с помощью специального математического программного обеспечения или с помощью таблиц и графиков, содержащих информацию об измерениях звезд.

Как использовать склонение звезды

Когда вы знаете склонение звезды, вы можете использовать его для ряда применений в астрономии:

Определение положения звезды на небесной сфере. Если вы знаете склонение звезды, вы можете найти ее точное положение на небе. Это особенно полезно для астрономов, которые хотят изучать связанные с ними явления, такие как затмения и планетарные соединения.
Определение движения звезды. Склонение звезды также может быть использовано для определения движения звезды в пространстве. Это может помочь астрономам понять, как звезды движутся и взаимодействуют друг с другом.
Определение принадлежности звезды к созвездию. Известные значения склонения звезд могут быть использованы для определения принадлежности звезды к определенному созвездию. Это особенно полезно для людей, которые хотят наблюдать звезды и планеты и хотят знать, в какую сторону неба искать.

Итог

Вычисление склонения звезды — это важный метод астрономического исследования, который может быть использован для определения различных характеристик звезды. Формула для вычисления склонения звезды включает в себя прямое восхождение звезды и звездное время. Знание склонения звезды можно использовать для определения положения звезды на небесной сфере, определения ее движения в пространстве и определения принадлежности к созвездию. Хотя вычисление склонения звезды может быть сложным, это очень важный инструмент для астрономов, и может помочь им лучше понять нашу вселенную.

Как найти склонение звезды формула астрономия

Звезды — это одни из самых важных объектов в космосе. Изучение звезд помогает нам лучше понимать устройство вселенной. Существует множество способов найти склонение звезды, но сегодня мы рассмотрим формулу астрономии, которая поможет найти склонение звезды с высокой точностью.

Что такое склонение звезды?

Склонение звезды — это угол между направлением к звезде и плоскостью экватора Земли. Склонение звезды измеряется в градусах и минутах и используется для нахождения местоположения звезды на небесной сфере.

Формула астрономии для нахождения склонения звезды

Формула астрономии для нахождения склонения звезды базируется на следующих данных:

Координаты звезды — прямое восхождение и склонение
Координаты наблюдателя на Земле — широта и долгота
Гринвичское звездное время

Формула выглядит следующим образом:

sin(склонение) = sin(широта) * sin(склонение_звезды) + cos(широта) * cos(склонение_звезды) * cos(часовой_угол_звезды)

Где:

склонение — искомый угол в градусах и минутах
широта — широта наблюдателя на Земле в градусах и минутах
склонение_звезды — склонение звезды в градусах и минутах
часовой_угол_звезды — разность между гринвичским звездным временем и прямым восхождением звезды в часах, минутах и секундах

Шаги для использования формулы астрономии

Для использования формулы астрономии для нахождения склонения звезды необходимо выполнить следующие шаги:

Найдите координаты звезды — прямое восхождение и склонение. Эту информацию можно найти в каталоге звезд или в Интернете.
Найдите координаты наблюдателя на Земле — широту и долготу. Эту информацию можно найти на карте или в Интернете.
Найдите гринвичское звездное время. Это время можно найти на Интернете.
Найдите часовой угол звезды, используя следующую формулу:

часовой_угол_звезды = гринвичское_звездное_время — прямое_восхождение_звезды

Подставьте значения в формулу астрономии для нахождения склонения звезды.
Вычислите значение склонения звезды, используя калькулятор или таблицу логарифмов.

Общий итог

Формула астрономии для нахождения склонения звезды — это один из множества способов для нахождения этого значения. Эта формула основывается на координатах звезды и наблюдателя на Земле и гринвичском звездном времени. Используя формулу и следуя вышеописанным шагам, можно найти склонение звезды с высокой точностью.

Как найти склонение звезды

Определение склонения звезды — это необходимое действие для астрономов, которые хотят найти точное место на небесной сфере. Склонение звезды выражается в градусах — это угол между плоскостью экватора и лучом, проведенным от наблюдателя к звезде. Это очень важный параметр, который используется во многих областях астрономии, таких как навигация в космосе, экспедиции на другие планеты и выполняемые научные исследования.

Используйте формулу для вычисления склонения

Формула для вычисления склонения звезды выглядит следующим образом:

Sin (δ) = Sin (φ) * Cos (H) * Cos (I) + Cos (φ) * Sin (I)

Где:

δ — склонение звезды
φ — широта наблюдателя
H — часовой угол
I — наклонение эклиптики

Часовой угол (H) представляет собой меру времени, прошедшего от местного полудня до момента наблюдения звезды. Наклонение эклиптики (I) показывает угол между экватором и эклиптикой — это плоскостью, которая определяет движение Солнца на небесной сфере.

Как использовать формулу

Для использования формулы вам понадобится определить точные значения параметров, которые в нее входят. Во-первых, вам нужно знать широту вашего местоположения. Широта определяется углом от экватора до места, где вы находитесь. Во-вторых, необходимо знать часовой угол наблюдателя. Он определяется как разность между местным временем и временем прохождения Солнца через часовой пояс. В-третьих, вам нужно знать наклонение эклиптики на момент наблюдения.

Как только вы знаете все эти параметры, вы можете вставить их в формулу, и она вычислит склонение звезды для вас.

Проверьте свои результаты

Кроме вычисления склонения звезды, вы также можете проверить свои результаты, используя различные астрономические инструменты, например, небесные карты или программное обеспечение для астрономии. Эти инструменты могут помочь вам определить, насколько точны ваше склонение звезды.

Заключение

Надеемся, что эта статья помогла вам понять, что такое склонение звезды, как его найти и использовать в астрономии. Формула для вычисления склонения может показаться сложной, но если вы знаете значения параметров, в нее входящих, то ее применение станет значительно проще.

Источник

Подвижная карта звездного неба позволяет определить вид звездного неба в любой момент суток произвольного дня года и быстро решать ряд практических задач на условия видимости небесных светил. На карте показаны созвездия, состоящие из ярких звезд до 3-ей звездной величины, а также некоторые более слабые звезды, дополняющие первичные очертания созвездий. Звезды изображены черными кружечками разных размеров. Основные звезды созвездий обозначены буквами греческого алфавита. Крупными тесно расположенных точек представлены яркие звездные скопления, а штриховой – яркие туманности. Полоса, выполненная в виде точек, изображает МЛЕЧНЫЙ ПУТЬ. В центре карты расположен Северный полюс мира и рядом с ним Полярная звезда (α Малой медведицы) . От Северного полюса мира расходятся радиусы, изображающие прямое восхождение (α), выраженное в часах. Начальный круг склонения, оцифрованный нулем (0)”, проходит через точку весеннего равноденствия, обозначенная знаком ¡. Диаметрально противоположный круг склонения с прямым восхождением α = 12 ч проходит через точку осеннего равнодействия . Концентрические окружности на карте изображают небесные параллели, а числа у точек их пересечения с нулевым (0 ч) и 12-ти часовым кругами склонения показывают их склонение (δ), выраженное в градусах. Третья по счету от Полюса мира окружность, оцифрованная 00, представляет собой небесный экватор, внутри которого расположена северная небесная полусфера, а вне его – пояс южной небесной полусферы до склонения δ = (-450). Так как в действительности диаметры небесных параллелей меньше диаметра небесного экватора, а на карте небесные параллели южной полусферы вынужденно изображены больших размеров, то вид созвездий южного неба несколько искажен, что следует иметь в виду при изучении звездного неба. Эклиптика изображена на карте эксцентрическим овалом, пересекающимся с небесным экватором в двух равнодействующих точках. На обрезе карты нанесены названия месяцев года и даты. Направление счета месяцев, дат и прямого восхождения – по вращению часовой стрелки. В этом же направлении следует изображать перемещение Солнца по эклиптике. В карте приложен накладной круг, внутри которого начерчены оцифрованные пересекающиеся овалы, а по обрезу нанесен часовой лимб, изображающий часы суток по среднему солнечному времени T l. Направление счета времени на этом лимбе – против часовой стрелки. Внутренний вырез в накладном круге делается по овалу, оцифрованному числом наиболее близким к географической широте местности, в которой карта будет использоваться. Контур овального выреза в наклонном круге изображает горизонт, и его основные точки обозначены буквами Ю (точка юга) , З (точка запада) , С (точка севера) и В (точка востока) . Между точками Ю и С необходимо натянуть темную нить, который изображают небесный меридиан. При работе с картой, накладной круг накладывается на карту всегда концентрично, причем нить (небесный меридиан) должна обязательно проходить через Северный полюс мира. Тогда отрезок нити, расположенный между Северным полюсом мира и точкой Ю, представит южную половину небесного меридиана, а остальной ее отрезок – северную ее половину. Наложив круг концентрично на карту, необходимо на нити отметить (хотя бы узелком) точку ее пересечения с небесной параллелью, склонение которой равно географической широте (или близко к ней) места наблюдений. Эта точка, лежащая вблизи центра накладного круга, изобразит зенит. Чтобы определить вид звездного неба на интересующий момент суток определенного дня года (даты) , достаточно наложить круг концентрично на карту (нить – меридиан проходит через Полюс мира) так, чтобы штрих момента времени совпадал со штрихом заданной карты, и тогда звезды, находящиеся в данный момент над горизонтом, окажутся расположенными внутри овального выреза.

Для определения склонения небесного светила необходимо месяц, число на звездной карте, совместить с часом наблюдения на накладной карте.

Источник

Обновлено: 17.05.2023

Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу от него.

* Объект на небесном экваторе имеет склонение 0°

* Склонение северного полюса небесной сферы равно +90°

Склонение южного полюса равно −90°У склонения всегда указывается знак, даже если оно положительно.

Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную со знаком −).

Связанные понятия

Прямое восхождение (α, R. A. — от англ. right ascension) — длина дуги небесного экватора от точки весеннего равноденствия до круга склонения светила. Прямое восхождение — одна из координат второй экваториальной системы (есть ещё и первая, в которой используется часовой угол). Вторая координата — склонение.

Небе́сный эква́тор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора. Небесный экватор делит небесную сферу на два полушария: северное полушарие, с вершиной в северном полюсе мира, и южное полушарие, с вершиной в южном полюсе мира. Созвездия, через которые проходит небесный экватор, называют экваториальными.

Небе́сная сфе́ра — воображаемая сфера произвольного радиуса, на которую проецируются небесные тела: служит для решения различных астрометрических задач. За центр небесной сферы принимают глаз наблюдателя; при этом наблюдатель может находиться как на поверхности Земли, так и в других точках пространства (например, он может быть отнесён к центру Земли). Для наземного наблюдателя вращение небесной сферы воспроизводит суточное движение светил на небе.

Полюс мира — точка на небесной сфере, вокруг которой происходит видимое суточное движение звёзд из-за вращения Земли вокруг своей оси. Направление на Северный полюс мира совпадает с направлением на географический север, а на Южный полюс мира — с направлением на географический юг. Северный полюс мира находится в созвездии Малой Медведицы с поляриссимой — Полярной звездой, южный — в созвездии Октант. В результате прецессии земной оси полюса мира смещаются примерно на 20 ” в год.

Упоминания в литературе

Экваториальную систему координат, которая строится на небесном экваторе, астрологи тоже применяют. Прямое восхождение (ά) и склонение (δ) – это две координаты, которые в данной системе определяют местонахождение небесного тела.

Вообще собственные движения звезд хоть и малы, но для ближайших звезд весьма заметны на больших промежутках времени. Например, нынешнее угловое склонение той же Альфы Центавра равно примерно минус 60°, то есть увидеть ее невозможно не только из средних, но и из субтропических северных широт. Однако древним египтянам эта звезда была хорошо знакома: в IV тысячелетии до н. э. она располагалась на небе всего в 30° южнее небесного экватора. Небесные объекты с таким склонением можно прекрасно наблюдать даже Крыму, не то что в Египте.

Локьер оставил достаточно практических советов для будущих астроархеологов. Он составил целый набор четких графиков для определения склонения звезды (для широт от 49° до 59°) от определенного азимута (рис. 11). Он справедливо отметил, какое значение имеет линия горизонта и как рефракция влияет на расчеты. По его мнению, линию горизонта можно примерно определить по контурным линиям на 1-дюймовых военно-топографических картах или их эквивалентах. Другими полезными цифрами являются изменения склонений самых ярких звезд, встречающиеся в расчетах древних жрецов-астрономов. Они показывают изменения склонения звезд (связанные с прецессией), рассчитанные на период от –2150 до –150. Изучение этих цифр подчеркивает одну из проблем, о которой уже упоминалось ранее (выше), то есть предварительно необходимо знать приблизительную дату(ы), когда именно проводилось какое-либо наблюдение за звездами. Например, если звезда № 26 (Спика, альфа Девы) и звезда № 25 (Бетельгейзе, альфа Ориона) находились на значительном расстоянии друг от друга в своем склонении в –2000, то примерно в –650 значения их склонения были такими же.

Связанные понятия (продолжение)

Галактическая система координат — это система небесных координат, имеющая начало отсчёта в Солнце и направление отсчёта от центра галактики Млечный Путь. Плоскость галактической системы координат совпадает с плоскостью галактического диска. Подобно географическим, галактические координаты имеют широту и долготу.

Экли́птика (от лат. (linea) ecliptica, от др.-греч. ἔκλειψις — затмение) — большой круг небесной сферы, по которому происходит видимое годичное движение Солнца. Соответственно плоскость эклиптики — плоскость обращения Земли вокруг Солнца (земной орбиты). Современное, более точное определение эклиптики — сечение небесной сферы плоскостью орбиты барицентра системы Земля — Луна.

Эклиптическая система координат, или эклиптикальные координаты:49 — это система небесных координат, в которой основной плоскостью является плоскость эклиптики, а полюсом — полюс эклиптики. Она применяется при наблюдениях за движением небесных тел Солнечной системы, плоскости орбит многих из которых, как известно, близки к плоскости эклиптики, а также при наблюдениях за видимым перемещением Солнца по небу за год:30.

Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.

Астрономи́ческая едини́ца (русское обозначение: а.е.; международное: с 2012 года — au; ранее использовалось обозначение ua) — исторически сложившаяся единица измерения расстояний в астрономии. Исходно принималась равной большой полуоси орбиты Земли, которая в астрономии считается средним расстоянием от Земли до Солнца:126.

Пятьдесят восемь навигационных звёзд имеют особый статус в области астрономической навигации. Из приблизительно 6000 звёзд, видимых невооруженным глазом в оптимальных условиях, выбранные звёзды являются одними из самых ярких и охватывают 38 созвездий на небесной сфере от склонения -70° до +89 °. Многие из навигационных звёзд были названы в древности вавилонянами, греками, римлянами и арабами.

Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.

Окта́нт (лат. Octans) — маленькое и очень тусклое созвездие южного полушария неба, включающее Южный полюс мира.

Предварение равноденствий (лат. praecessio aequinoctiorum) — историческое название для постепенного смещения точек весеннего и осеннего равноденствий (то есть точек пересечения небесного экватора с эклиптикой) навстречу видимому годичному движению Солнца. Другими словами, каждый год весеннее равноденствие наступает немного раньше, чем в предыдущем году — примерно на 20 минут 24 секунды. В угловых единицах смещение составляет сейчас примерно 50,3″ в год, или 1 градус каждые 71,6 года. Это смещение.

Радиа́нт (лат. radians, род. п. лат. radiantis — излучающий) — область небесной сферы, кажущаяся источником метеоров, которые наблюдаются при встрече Земли с роем метеорных тел, движущихся вокруг Солнца по общей орбите.

Покры́тие — это астрономическое явление, во время которого, с точки зрения наблюдателя из определённой точки, одно небесное тело проходит перед другим небесным телом, заслоняя его часть.

Кульминация (астрономия) — прохождение центра светила через небесный меридиан в процессе его суточного движения. Иначе — прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.

В списке приведены самые яркие звёзды, наблюдаемые с Земли, в оптическом диапазоне по видимой звёздной величине. Для кратных звёзд приведена суммарная звёздная величина.

Ма́сса Земли́ (в астрономии обозначается M⊕, где ⊕ — символ Земли) — масса планеты Земля, в астрономии используется как внесистемная единица массы. 1 M⊕ = (5,9722 ± 0,0006) × 1024 кг.

Фе́никс (лат. Phoenix, Phe) — созвездие южного полушария неба. Занимает на небе площадь в 469,3 квадратного градуса, содержит 68 звёзд, видимых невооружённым глазом.

Спектрально-двойной — называют систему двойных звёзд, если двойственность обнаруживается при помощи спектральных наблюдений. Обычно это системы, у которых скорости компонентов достаточно велики, а расположены они настолько близко, что увидеть их раздельно с использованием современных телескопов невозможно. В результате орбитального движения звёзд вокруг центра масс одна из них приближается к нам, а другая от нас удаляется, их лучевые скорости (вдоль направления на наблюдателя) неодинаковы и, как.

Науго́льник (лат. Norma) — созвездие южного полушария неба, лежит к юго-западу от Скорпиона, севернее Южного Треугольника, в контакте с Циркулем. Через него проходят обе ветви Млечного Пути, но эта область неба бедна яркими звёздами. Созвездие не содержит звёзд ярче 4,0 визуальной звёздной величины, 42 звезды, видимые невооружённым глазом, площадь на небе 165,3 квадратного градуса. Наилучшие условия для наблюдений в мае — июне, частично наблюдается в южных районах России (к югу от 48 С.Ш). В созвездии.

Же́ртвенник (лат. Ara) — созвездие южного полушария неба. Площадь 237,0 кв. градуса, 60 звёзд, видимых невооружённым глазом. На юге России (южнее широты 44° 30′) небольшая часть созвездия (но без ярких звёзд) восходит совсем низко над горизонтом в мае-июне. Звезда α Жертвенника (звёздная величина 2,95) в России не наблюдается, но при благоприятных условиях заметна вблизи линии горизонта в южных городах постсоветского пространства, расположенных южнее широты 40° 08′ (Бухаре, Самарканде, Нахичевани.

Золота́я Ры́ба (порт. Dorado от лат. Doradus) — созвездие южного полушария неба. Занимает на небе площадь в 179,2 квадратного градуса. Содержит 32 звезды, видимых невооружённым глазом.

В этот список ближайших к Земле звёзд, отсортированный в порядке увеличения расстояния, вошли звёзды, расположенные в радиусе 5 пк (16,308 св. года) от Земли. Включая Солнце, в настоящее время известны 57 звёздных систем, которые могут находиться в пределах этого расстояния. Эти системы содержат в общей сложности 64 звезды и 13 коричневых карликов.

Прохожде́ние, или астрономи́ческий транзи́т — это астрономическое явление, во время которого с точки зрения наблюдателя из определённой точки одно небесное тело проходит перед другим небесным телом, заслоняя его часть.

Возни́чий (лат. Auriga) — созвездие северного полушария неба. Самая яркая звезда — Капелла, 0,1 визуальной звёздной величины. Наиболее благоприятные условия видимости в декабре — январе. Видно на всей территории России.

Синоди́ческий пери́од обраще́ния (от греч. σύνοδος — соединение) — промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.

Микроско́п (лат. Microscopium) — небольшое созвездие южного полушария неба. Лежит к югу от Козерога, к северу от Индейца, восточнее Стрельца и западнее Южной Рыбы и Журавля.

Орёл (лат. Aquila) — экваториальное созвездие. Западная его часть лежит в восточной ветви Млечного Пути, южнее Стрелы. Площадь созвездия — 652,5 квадратного градуса, число звёзд ярче 6m — 70.

International Celestial Reference System (ICRS, Международная небесная система координат или Международная система астрономических координат) — с 1998 года стандартная небесная система координат. Принята на 23-м съезде МАС в 1997 году. Началом отсчёта является барицентр Солнечной системы. Координаты в этой системе максимально приближены к экваториальным эпохи J2000.0 (расхождение составляет доли секунды дуги).

Переменные звезды имеют специальные обозначения, если они ещё не были обозначены буквой греческого алфавита, в формате обозначения Байера, в сочетании с именем созвездия в родительном падеже, в котором эта звезда находится. (см. Список созвездий и их латинское название (родительный падеж)).

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Звёздные су́тки — период вращения какого-либо небесного тела вокруг собственной оси в инерциальной системе отсчёта, за которую обычно принимается система отсчёта, связанная с удалёнными звёздами. Для Земли это время, за которое Земля совершает один оборот вокруг своей оси по отношению к далёким звёздам.

Абсолютная звёздная величина — физическая величина, характеризующая светимость астрономического объекта. Для разных типов объектов используются разные определения абсолютной величины.

Живопи́сец (лат. Pictor) — маленькое созвездие южного полушария неба. Занимает на небе площадь в 247,7 квадратного градуса, содержит 49 звёзд, видимых невооружённым глазом. На юге России (южнее широты +47°) восходит небольшая часть созвездия (но без ярких звёзд). Первая относительно яркая звезда созвездия – β Живописца (её звёздная величина 3,85) восходит южнее широты +38°56′ (в пределах территории бывшего СССР она восходит в Душанбе, Астаре, Ашхабаде, Кушке). В созвездии Живописца находится звезда.

Се́тка (лат. Reticulum, Ret) — созвездие южного полушария неба. Занимает на небе площадь в 113,9 квадратного градуса, содержит 22 звезды, видимые невооружённым глазом.

Компас (лат. Pyxis, Pyx) — созвездие южного полушария неба. Занимает на небе площадь в 220,8 квадратного градуса, содержит 43 звёзды, видимые невооружённым глазом. На территории России полностью наблюдается в южных районах, а также на юге центральных. Лучшее время года для наблюдения — февраль-март.

Единоро́г (лат. Monoceros от греч. μονόκερως), экваториальное созвездие. Занимает на небе площадь в 481,6 квадратного градуса и содержит 146 звёзд, видимых невооружённым глазом. Лежит в Млечном пути, однако ярких звёзд не содержит. Местонахождение созвездия — внутри зимнего треугольника, образованного яркими звёздами — Сириусом, Проционом и Бетельгейзе, по которым его легко найти. Единорог — одно из 15 созвездий, через которые проходит линия небесного экватора. Видно в центральных и южных районах.

Тука́н (лат. Tucana, Tuc) — созвездие южного полушария неба. Занимает на небе площадь в 294,6 квадратного градуса, содержит 44 звезды, видимые невооружённым глазом.

Накло́н о́си враще́ния — угол отклонения оси вращения небесного тела от перпендикуляра к плоскости его орбиты. Другими словами — угол между плоскостями экватора небесного тела и его орбиты.

Упоминания в литературе (продолжение)

Для удобства описания границ созвездий их решено было проводить в виде ломаных линий, проходящих точно по сетке постоянных небесных координат – склонений и прямых восхождений. При этом созвездия стали напоминать некоторые африканские страны и американские штаты, границы которых проведены по параллелям и меридианам. Ну что же, это вполне рациональный способ, позволяющий легко закрепить границы в математической форме. Однако со временем в этой изящной идее стал проявляться один мелкий недостаток.

Род определяется по окончаниям им. п. ед. ч., свойственным определенному роду в пределах данного склонения. Следовательно, для того чтобы определить род любого существительного III склонения, надо учитывать три момента:

Существительные III склонения встречались крайне редко, например: os, corpus, caput, foramen, dens. Такой методический подход был абсолютно оправдан. III склонение – самое трудное для усвоения и имеет ряд особенностей, отличающих его от остальных склонений.

Часы, изготовленные человеком, измеряют пренебрежимо малые с эволюционной точки зрения доли – часы, минуты, секунды – и поэтому основаны на быстрых динамических процессах: качании маятника, раскручивании пружины, колебаниях кристаллов, горении свечи, вытекании воды из сосуда или высыпании песка, вращении Земли (определяемом по движению солнечной тени). Эти процессы протекают с известной постоянной скоростью. Маятник качается с известной частотой, определяемой, по крайней мере в теории, только его длиной, но не амплитудой колебаний и не массой груза на его конце. Напольные часы работают благодаря присоединению маятника к анкеру, передающему движение зубчатому колесу, которое при помощи системы шестеренок обеспечивает ход секундной, минутной и часовой стрелок. Пружинные часы работают почти так же. Кварцевые часы работают при помощи эквивалента маятника – колебаний кристаллов определенного вида под воздействием энергии, поставляемой батарейкой. Водяные и огненные часы обладают куда меньшей точностью, но ими широко пользовались до изобретения часов, основанных на постоянстве хода. Они основаны не на подсчете отрезков времени, как маятниковые или цифровые часы, а на измерении объема. Солнечные часы – неточный способ измерения времени. Однако вращение Земли позволяет создать более точные, хотя и медленные часы, которые мы называем календарем. Это происходит именно потому, что при таком масштабе часы становятся не измеряющими (как солнечные часы, измеряющие постоянно меняющееся склонение солнца), а счетными (подсчитывающими число циклов день/ночь).

Чем больше вы узнаете о звездах и их движениях, тем больший интерес будут представлять их наблюдения. Небесный глобус поможет вам найти объекты на небе, так же как земной глобус помогает отыскать нужные места на Земле.

Вспомните, как работают с картой Земли. Мы рисуем земную поверхность и наносим на ней воображаемую координатную сетку. Местоположения всех точек отсчитываются от двух основных нулевых линий. Одна из них – экватор – это большой круг на полпути между северным и южным полюсами, который делит глобус на два равных полушария. Другая – начальный меридиан – проходит от полюса до полюса через Гринвич (Англия).

Воображаемые линии, параллельные экватору, называются линиями равных широт или параллелями. Такие же линии, проходящие через полюса, называются линиями равных долгот или меридианами. Расстояния на земной сфере измеряются в градусах путем деления круга на 360 частей.

На Земле можно найти любой город, если известны его координаты (широта и долгота).

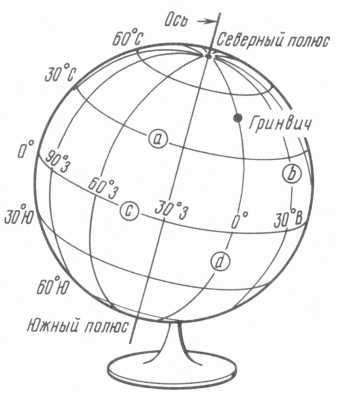
Глобус Земли

Подобно тому как наносят на земной глобус линии широт и долгот, астрономы наносят воображаемые вертикальные и горизонтальные линии на небесную сферу. Угловые расстояния вверх и вниз от небесного экватора называются склонениями (δ). Угловое расстояние от нулевой точки на небесном экваторе (точки весеннего равноденствия), отсчитываемое в восточном направлении, называется прямым восхождением (α). Прямое восхождение обычно измеряется в часах, причем 1 h = 15°.

Так же как на Земле любой город может быть найден по его земным координатам – широте и долготе, любой небесный объект может быть найден по его небесным координатам – прямому восхождению и склонению.

Небесный глобус

Каждая звезда занимает на небесной сфере вполне определенное место. Прямые восхождения и склонения звезд с течением времени изменяются очень мало и могут быть определены с помощью звездного глобуса или звездных атласов (см. таблицу: “Двадцать самых ярких звезд в порядке уменьшения блеска”).

Таблица – Двадцать самых ярких звезд в порядке уменьшения блеска

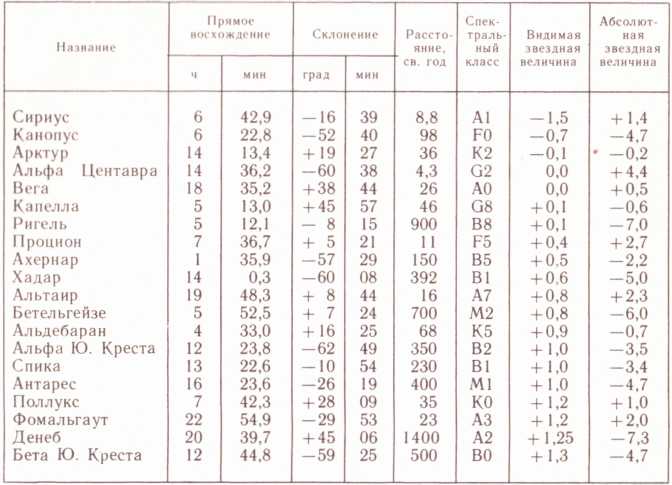
Положение Солнца, Луны и планет на небесной сфере постоянно изменяется. Их координаты приводятся в периодических астрономических изданиях.

Можете ли вы объяснить, почему на протяжении любого достаточно длительного промежутка времени звезды могут быть найдены на небесной сфере по тем же самым координатам, в то время как Солнце, Луна и планеты постоянно изменяют свое положение?

– Звезды слишком далеки от Земли, чтобы их движение было заметно невооруженным глазом, хотя они двигаются в различных направлениях со скоростями во много километров в секунду. Солнце же, Луна и планеты гораздо ближе к Земле. Мы видим их перемещение на фоне далеких звезд.

2. Видимое суточное движение звёзд. При наблюдении звёздного неба на протяжении одного-двух часов мы убеждаемся в том, что оно вращается как единое целое таким образом, что с одной стороны звёзды поднимаются, а с другой — опускаются. Для нас, жителей Северного полушария, звёзды поднимаются с восточной части горизонта и смещаются вправо. Далее они достигают наивысшего положения в южной части неба и затем опускаются в западной части горизонта. В течение суток звёздное небо со всеми находящимися на нём светилами совершает один оборот. Таким образом, видимое суточное вращение звёздного неба происходит с востока на запад, если стоять лицом к югу, т. е. по часовой стрелке.

В северной части неба можно отыскать Полярную звезду. Кажется, что всё небо вращается вокруг неё (рис. 10). На самом же деле вокруг своей оси вращается Земля с запада на восток, а весь небосвод вращается в обратном направлении с востока на запад. Полярная звезда для данной местности остаётся почти неподвижной и на одной и той же высоте над горизонтом. Очевидно, что суточное движение звёзд (светил) — наблюдаемое кажущееся явление вращения небесного свода — отражает действительное вращение земного шара вокруг оси.

Фильм. Небесная сфера, координаты.

3. Основные точки, линии и плоскости небесной сферы. Нам кажется, что все звёзды расположены на некоторой сферической поверхности неба и одинаково удалены от наблюдателя. На самом деле они находятся от нас на различных расстояниях. Поэтому воображаемую поверхность небосвода стали называть небесной сферой.
Небесная сфера — это воображаемая сфера произвольного радиуса, центр которой в зависимости от решаемой задачи совмещается с той или иной точкой пространства. Центр небесной сферы может быть выбран в месте наблюдения (глаз наблюдателя), в центре Земли или Солнца и т. д. Понятием небесной сферы пользуются для угловых измерений, для изучения взаимного расположения и движения космических объектов на небе.

Рис. 11. Схема проецирования звезд в созвездии Большой Медведицы на небесной сфере

Прямая, проходящая через центр небесной сферы (рис. 12) и совпадающая с направлением нити отвеса в месте наблюдения, называется отвесной или вертикальной линией . Она пересекает небесную сферу в точках зенита (верхняя точка пересечения отвесной линии с небесной сферой) и надира (точка небесной сферы, противоположная зениту). Плоскость, проходящая через центр небесной сферы и перпендикулярная отвесной линии, называется плоскостью истинного или математического горизонта.

Большой круг небесной сферы, проходящий через зенит, светило и надир, называется кругом высоты , вертикальным кругом или просто вертикалом светила .

Ось мира — прямая, проходящая через центр небесной сферы параллельно оси вращения Земли, пересекающая небесную сферу в двух диаметрально противоположных точках.

Рисунок 12 — Небесная сфера: О — центр небесной сферы (местонахождение наблюдателя); PN — Северный полюс мира; РS — Южный полюс мира; PNPS — ось мира; Z — зенит; Z’ — надир; E — восток; W — запад; N — север; S — юг; Q — верхняя точка небесного экватора; Q’ — нижняя точка небесного экватора; ZZ’ — вертикальная линия; PNMPS — круг склонения; NS — полуденная линия; M — светило на небесной сфере

Рисунок 13 — Эклиптика

Точка пересечения оси мира с небесной сферой, вблизи которой находится Полярная звезда, называется Северным полюсом мира, противоположная точка — Южным полюсом мира . Полярная звезда отстоит от Северного полюса мира на угловом расстоянии около 1° (точнее 44′).
Большой круг, проходящий через центр небесной сферы и перпендикулярный оси мира, называют небесным экватором. Он делит небесную сферу на две части: Северное полушарие с вершиной в Северном полюсе мира и Южное — с вершиной в Южном полюсе мира.

Круг склонения светила — большой круг небесной сферы, проходящий через полюсы мира и светило.

Суточная параллель — малый круг небесной сферы, плоскость которого перпендикулярна оси мира.

Большой круг небесной сферы, проходящий через точки зенита, надира и полюсы мира, называется небесным меридианом . Небесный меридиан пересекается с истинным горизонтом в двух диаметрально противоположных точках. Точка пересечения истинного горизонта и небесного меридиана, ближайшая к Северному полюсу мира, называется точкой севера . Точка пересечения истинного горизонта и небесного меридиана, ближайшая к Южному полюсу мира, называется точкой юга . Линия, соединяющая точки севера и юга, называется полуденной линией . Она лежит на плоскости истинного горизонта. По направлению полуденной линии падают тени от предметов в полдень.

С небесным экватором истинный горизонт также пересекается в двух диаметрально противоположных точках — точке востока и т очке запада . Для наблюдателя, стоящего в центре небесной сферы лицом к точке севера, точка востока будет расположена справа, а точка запада — слева. Помня это правило, легко ориентироваться на местности.

Видимый годовой путь Солнца среди звёзд называется эклиптикой. В плоскости эклиптики лежит путь Земли вокруг Солнца, т. е. её орбита. Она наклонена к небесному экватору под углом 23° 27′ и пересекает его в точках весеннего (ϒ, около 21 марта) и осеннего (Ω, около 23 сентября) равноденствия (рис. 13).

§ 3. Небесные координаты

1. Системы координат. Положение светил определяется по отношению к точкам и кругам небесной сферы (см. рис. 12). Для этого введены небесные координаты, подобные географическим координатам на поверхности Земли.

В астрономии применяется несколько систем координат. Отличаются они друг от друга тем, что строятся по отношению к разным кругам небесной сферы. Небесные координаты отсчитываются дугами больших кругов или центральными углами, охватывающими эти дуги.

Небесные координаты — центральные углы или дуги больших кругов небесной сферы, с помощью которых определяют положение светил по отношению к основным кругам и точкам небесной сферы.

Рисунок 14 — Горизонтальная система координат: h — высота светила й над горизонтом; z — зенитное расстояние; А — азимут

Горизонтальная система координат . При астрономических наблюдениях удобно определять положение светил по отношению к горизонту. Горизонтальная система координат использует в качестве основного круга истинный горизонт. В этой системе координатами являются высота (h) и азимут (А).

Высота светила — угловое расстояние светила М от истинного горизонта, измеренное вдоль вертикального круга (рис. 14). Высота определяется в градусах, минутах и секундах. Она отсчитывается в пределах от 0 до +90° к зениту, если светило находится в видимой части небесной сферы, и от 0 до -90° к надиру, если светило находится под горизонтом.

Для измерения азимутов за начало отсчёта принимается точка юга. Азимут светила — угловое расстояние, измеренное вдоль истинного горизонта, от точки юга до точки пересечения горизонта с вертикальным кругом, проходящим через светило М (см. рис. 14). Азимут отсчитывается к западу от точки юга в пределах от 0 до 360°.

Горизонтальная система координат используется при топографической съёмке, в навигации. Вследствие суточного вращения небесной сферы высота и азимут светила со временем изменяются. Следовательно горизонтальные координаты имеют определённое значение только для известного момента времени.

Угловое расстояние от зенита до светила, измеренное вдоль вертикального круга, называется зенитным расстоянием (z). Оно отсчитывается в пределах от 0 до +180° к надиру. Высота и зенитное расстояние связаны соотношением: z + h = 90°.

Рисунок 15 — Экваториальная система небесных координат: δ — склонение светила М; α — прямое восхождение; t — часовой угол

Экваториальная система координат. Для построения звёздных карт и составления звёздных каталогов за основной круг небесной сферы удобно принять круг небесного экватора (рис. 15). Небесные координаты, в системе которых основным кругом является небесный экватор, называются экваториальной системой координат. В этой системе координатами служат склонение ( δ ) и прямое восхождение ( α ).
Склонение светила — угловое расстояние светила М от небесного экватора, измеренное вдоль круга склонения. Склонение отсчитывается в пределах от 0 до +90° к Северному полюсу мира и от 0 до -90° к Южному полюсу мира.

За начальную точку отсчёта на небесном экваторе принимается точка весеннего равноденствия γ , где Солнце бывает около 21 марта.

Прямое восхождение светила — угловое расстояние, измеренное вдоль небесного экватора, от точки весеннего равноденствия до точки пересечения небесного экватора с кругом склонения светила. Прямое восхождение отсчитывается в сторону, противоположную суточному вращению небесной сферы, в пределах от 0 до 360° в градусной мере или от 0 до 24 ч в часовой мере.

Для некоторых астрономических задач (связанных с измерением времени) вместо прямого восхождения (а) вводится часовой угол (t) (см. рис. 15). Часовой угол — это угловое расстояние, измеренное вдоль небесного экватора, от верхней точки небесного экватора до круга склонения светила. Отсчитывается часовой угол по направлению видимого суточного вращения небесной сферы, т. е. к западу, в пределах от 0 до 24 ч в часовой мере.

Координаты звёзд (α, δ) в экваториальной системе координат не связаны с суточным движением небесной сферы и изменяются очень медленно. Поэтому они применяются для составления звёздных карт и каталогов. Звёздные карты представляют собой проекции небесной сферы на плоскость с нанесёнными на неё объектами в определённой системе координат. Онлайн карта звёздного неба. Набор звёздных карт смежных участков неба, покрывающих всё небо или некоторую его часть, называется звёздным атласом. В специальных списках звёзд, называемых звёздными каталогами, указываются координаты их места на небесной сфере, звёздная величина и другие параметры. Например, каталог Hubble Guide Star Catalog (GSC) содержит почти 19 млн объектов.

Рисунок 16 — Высота полюса мира над горизонтом

2. Лунно-солнечная прецессия. Ось вращения Земли наклонена к плоскости орбиты под углом 66°33′. Под воздействием притяжения Луны и Солнца из-за неоднородности распределения плотности массы внутри Земли ось описывает конус. Так как направление оси Земли изменяется, то перпендикулярная ей плоскость экватора также будет смещаться, что приводит к перемещению точки весеннего равноденствия. Это явление называется лунно-солнечной прецессией. Точка весеннего равноденствия перемещается навстречу видимому годичному движению Солнца на 50,3″ в год или на 1° в 71,6 года, совершая полный оборот по эклиптике за 25 770 лет. Полюса мира также перемещаются среди звёзд. В настоящее время Северный полюс мира находится возле Полярной звезды, а через 10 тыс. лет он переместится к Веге ( a Лиры).

3. Высота полюса мира над горизонтом. Мы уже знаем, что Полярная звезда, находящаяся вблизи Северного полюса мира, остаётся почти на одной высоте над горизонтом на данной широте при суточном вращении звёздного неба. При перемещении наблюдателя с севера на юг, где географическая широта меньше, Полярная звезда опускается к горизонту, т. е. существует зависимость между высотой полюса мира и географической широтой места наблюдения.

На рисунке 16 земной шар и небесная сфера изображены в сечении плоскостью небесного меридиана места наблюдения. Наблюдатель из точки О видит полюс мира на высоте Ð NOP = h_P. Направление оси мира ОР параллельно земной оси. Угол при центре Земли Ð OO’q соответствует географической широте места наблюдения ф. Так как радиус Земли в точке наблюдения перпендикулярен плоскости истинного горизонта, а ось мира перпендикулярна плоскости географического экватора, то Ð NOP и Ð OO’q равны между собой как углы с взаимно перпендикулярными сторонами. Таким образом, угловая высота полюса мира над горизонтом равна географической широте места наблюдения:

С другой стороны, из рисунка 16 следует, что Ð QOZ определяет собой величину склонения зенита d_Z. Поэтому можно записать, что

Равенство (2) характеризует зависимость между географической широтой места наблюдения и соответствующими горизонтальной и экваториальной координатами светила.

Суточное вращение звёздного неба на средних широтах

Суточное вращение звёздного неба на земном экваторе

По мере перемещения наблюдателя к Северному полюсу Земли Северный полюс мира поднимается над горизонтом. На полюсе Земли полюс мира будет находиться в зените. Звёзды здесь движутся по кругам, параллельным горизонту, который совпадает с небесным экватором. Становится неопределённым небесный меридиан, теряют смысл точки севера, юга, востока и запада.

На средних географических широтах ось мира и небесный экватор наклонены к горизонту, суточные пути звёзд также наклонены к горизонту. Поэтому наблюдаются восходящие и заходящие звёзды. Под восходом понимается явление пересечения светилом восточной части горизонта, а под заходом — западной части горизонта. В средних широтах, например на территории Республики Беларусь, наблюдаются звёзды северных околополярных созвездий, которые никогда не опускаются под горизонт. Они называются незаходящими . Звёзды, расположенные около Южного полюса мира, у нас никогда не восходят. Их называют невосходящими .

На экваторе Земли ось мира совпадает с полуденной линией, а полюсы мира — с точками севера и юга. Небесный экватор проходит через точки востока, запада, точки зенита и надира. Суточные пути всех звёзд перпендикулярны горизонту, и каждая из них половину суток находится над горизонтом.

Для определения склонения небесного светила необходимо месяц, число на звездной карте, совместить с часом наблюдения на накладной карте

Читайте также:

Оккультизм что это кратко

Почему важно чтобы каждый человек был ответственным кратко

Чем близок чацкому князь федор ответ кратко

Титульный лист календарного плана в доу по фгос

Отчет куратора о работе с курируемой школой участницей проекта 500

Источник

У этого термина существуют и другие значения, см. Склонение.

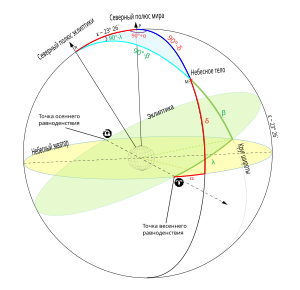
Экваториальные и эклиптические координаты небесных тел. Склонение обозначено delta

Склонение в астрономии (обозначается или dec — от англ. declination) — координата объекта на небесной сфере, которая не меняется при суточном вращении Земли. Склонение равно угловому расстоянию на небесной сфере от плоскости небесного экватора до светила, оно положительно для объектов в северном полушарии и отрицательно — в южном.

Описание[править | править код]

В экваториальной системе небесных координат одной из двух координат является склонение. Склонение светила — дуга круга склонений между ним и плоскостью экватора^[1]^[2], или, проще говоря, угловое расстояние между светилом и небесным экватором. Склонение считается положительным, если светило находится в северном полушарии небесной сферы, и отрицательным — если в южном. Таким образом, склонение может находиться в диапазоне от −90° до +90°^[3]^[4], причём эти значения достигаются, соответственно, на южном и на северном полюсах мира, а на небесном экваторе склонение равно нулю^[5].

Склонение принято обозначать delta или dec (от англ. declination)^[3]^[6]. В редких случаях его могут заменять полярным расстоянием , которое равно угловому расстоянию между светилом и северным полюсом мира, таким образом, ${displaystyle p=90^{circ }-delta }$ и эта величина меняется от 0 до 180°^[1].

В первой экваториальной системе координат дополнительно к склонению используется часовой угол светила , а во второй экваториальной — прямое восхождение alpha . Склонение, как и прямое восхождение не меняются из-за суточного вращения Земли, поэтому вторая экваториальная система используется наиболее широко^[7].

Суточное движение светил[править | править код]

Склонение светила связано с высотами его верхней и нижней кульминации ${displaystyle h_{text{в}}}$ и ${displaystyle h_{text{н}}}$ посредством географической широты места наблюдения varphi , причём широты в южном полушарии считаются отрицательными. Формулы для ${displaystyle h_{text{в}}}$ примут разный вид в зависимости от соотношения между varphi и delta ^[8]^[9]:

если

, то ${displaystyle h_{text{в}}=90^{circ }-varphi +delta }$

и верхняя кульминация происходит к югу от зенита;

если

, то ${displaystyle h_{text{в}}=90^{circ }+varphi -delta }$

и верхняя кульминация происходит к северу от зенита;

если

, то верхняя кульминация происходит точно в зените, на высоте ${displaystyle h_{text{в}}=90^{circ }}$

Высота нижней кульминации определяется формулой ${displaystyle h_{text{н}}=varphi +delta -90^{circ }}$ ^[10].

Если ${displaystyle h_{text{н}}>0}$ , то светило никогда не заходит под горизонт и называется незаходящим; если ${displaystyle h_{text{в}}<0}$ , то светило никогда не восходит из-за горизонта и называется невосходящим. Таким образом, если ${displaystyle |delta |<90^{circ }-|varphi |}$ , то в ходе суточного движения светило восходит и заходит. Для северного полушария, если ${displaystyle delta >90^{circ }-varphi }$ , то светило является незаходящим, если ${displaystyle delta <varphi -90^{circ }}$ — невосходящим^[11]^[12].

Положения восхода и захода светил, если они возможны, также зависят от склонения. Светила с нулевым склонением восходят на востоке и заходят на западе, тогда как при восход и заход происходят на северо-востоке и северо-западе соответственно, а при — на юго-востоке и на юго-западе^[11].

Со склонением светила и широтой места наблюдения можно также связать часовой угол и азимут точки , где происходит его восход и заход^[13]:

{displaystyle cos t=-tan delta tan varphi }

Если данное уравнение не имеет решений, то светило является незаходящим или невосходящим; если решение только одно, то светило касается горизонта в верхней либо в нижней кульминации, что возможно при ${displaystyle varphi -delta =90^{circ }}$ или ${displaystyle varphi +delta =90^{circ }}$ . В остальных случаях уравнение имеет два решения, $t_{r}$ и $t_{s}$ , причём ${displaystyle 180^{circ }<t_{r}<360^{circ }}$ и $t_{r}$ соответствует восходу, а ${displaystyle 0^{circ }<t_{s}<180^{circ }}$ и $t_{s}$ соответствует заходу. Азимут точек восхода и захода определяется из системы уравнений^[13]:

{displaystyle cos A=-sin delta cos varphi +cos delta sin varphi cos t}

Склонение Солнца[править | править код]

Склонение и прямое восхождение Солнца меняются в течение года из-за вращения Земли вокруг Солнца. В момент весеннего равноденствия Солнце находится в точке весеннего равноденствия, и его склонение и прямое восхождение равны нулю. После этого склонение Солнца начинает увеличиваться и доходит до максимального значения — 23°26′ — в момент летнего солнцестояния, и в этот момент его прямое восхождение равняется 6^h. После этого оно начинает уменьшаться: в момент осеннего равноденствия склонение снова равняется нулю, а прямое восхождение — 12^h. В момент зимнего солнцестояния склонение достигает своего минимума — −23°26′ (прямое восхождение равно 18^h), после чего снова начинает расти и доходит до нуля в момент весеннего равноденствия. Таким образом, в разные сезоны световой день длится по-разному, а в приполярных областях бывают полярные дни и полярные ночи^[14].

Влияние прецессии[править | править код]

Из-за прецессии оси Земли меняется положение полюсов мира и небесного экватора с периодом в 26000 лет, следовательно, даже у неподвижных объектов меняется склонение и прямое восхождение. Для точной записи координат необходимо учитывать момент времени, в который они были измерены, называемый эпохой. Координаты также можно пересчитать для другой эпохи, и в данный момент в основном используется эпоха J2000.0, которой соответствует момент полудня 1 января 2000 года^[15].

Примечания[править | править код]

↑ ¹ ² Жаров, 2006, с. 75—76.
↑ Склонение. Большая российская энциклопедия. Дата обращения: 25 января 2023.
↑ ¹ ² Karttunen et al., 2016, p. 17.
↑ Кононович, Мороз, 2004, с. 20—21.
↑ Declination (англ.). Encyclopedia Britannica. Дата обращения: 27 января 2023.
↑ Celestial Coordinates. spiff.rit.edu. Дата обращения: 25 января 2023.
↑ Кононович, Мороз, 2004, с. 21—22.
↑ Кононович, Мороз, 2004, с. 17, 25.
↑ Жаров, 2006, с. 94—95.
↑ Кононович, Мороз, 2004, с. 25.
↑ ¹ ² Кононович, Мороз, 2004, с. 23.
↑ Karttunen et al., 2016, pp. 19—20.
↑ ¹ ² Жаров, 2006, с. 96—97.
↑ Кононович, Мороз, 2004, с. 27—28.
↑ Karttunen et al., 2016, pp. 22—23.

Литература[править | править код]

Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
Жаров В. Е. Сферическая астрономия. — Фрязино: Век 2, 2006. — 480 с. — (Монографии и учебники). — 500 экз. — ISBN 5-85099-168-9.
Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 6th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2016. — 550 p. — ISBN 978-3-662-53045-0.

Источник

Величины
даются в принятых в таблицах МАЕ и на
бланке Ш8Б обозначениях.

Рассчитываем
приближённое время и дату на меридиане
Гринвича по формуле:

,
где

номер
часового пояса, рассчитывается с
точностью до 1м по формуле:

и округляется в
ближайшую сторону.

Смотрим, изменилась
ли дата.

По
известным Т_ХР
для каждого светила и U_ХР
рассчитываем точноеТ_ГРс точностью до 1^спо формуле:

В
ежедневных таблицахМАЕна
полученную датуипо целому количеству
часовТ_ГРв колонке
т.Овна выбираем значениеt_T(градусы минуты).
В
основных интерполяционных таблицахМАЕпо минутам и секундамгринвичского
времениТ_ГР,в таблице
минутпо количествусекунд в
колонке т.Овна выбираем поправку₁t(градусы минуты).
Суммированием
получаем гринвичский часовой угол t_ГР.
Выписываем
заданную (счислимую) долготу ,
прибавляем со своим знаком (+O^st
–W) кt_ГР.
Получаем местный часовой угол т.Овнаt_м^
Из
таблицы «Звёзды. Видимые места»с
левой стороны разворота по наименованию
звезды выбираем звёздное дополнение*.
Причём целое количество градусов
выбирается из колонки следующей за
названием светила, а минуты из колонки
по ближайшей дате.
В этой
же таблице с правой стороны выбирается
склонение .
Причём целое количество градусов и
наименование выбирается из колонки
следующей за собственным именем светила,
а минуты из колонки по ближайшей дате.
Суммируем
значения t_м^и*,
получаемвестовоезначение местного
часового углаt_Wв круговом счёте(если полученное
значение больше 360,
отбрасываем 360).
Получаем
часовой угол в полукруговом счёте. Если
полученное значение t_Wменее 180, то оно
остаётся без изменений, если более
180, то по формулеt_Ost
= 360– t_Wполучаем остовое значение часового
угла.

Расчёт
местного часового угла t_Ми
склонениязвезды.

Дано:
24/06 1993 _C= 0707,7NТхр = 00^ч17^м37^с

Тс=00^ч30^м_C= 8415,8WUхр
= +12^м33^с

Большой Медведицы.

Действие	Пример для бланка Ш8Б	Пояснения
		 Большой Медведицы
		1 линия
Рассчитываем приближённое Т_ГР(§ 9)	Приб. Т_С	18^ч 30^м	20^ч 18^м 30/04+10^ч=06^ч 18^м 01/05 Так как результат больше 24^ч, отбрасываем 24 и дату увеличиваем на 1 сутки
	+06
Приб. Т_ГР	00^ч 30^м
Дата	25/06
Рассчитываем точное Т_ГР(§ 9)	Т_ХР	0^ч 17^м 37^с	По приб. Т_ГР видим, что на Гринвиче первая половина дня. Следовательно, к точному Т_ГР 12^ч не прибавляем.
U_ХР	+ 12^ч 33^м
Т_ГР	0^ч 30^м 10^с
Рассчитываем гринвичское звёздное время (гринвичский часовой угол т. Овна t_ГР).	t_T	273º 08,7	Ежедневные Таблицы МАЕ. На гринвичскую дату по часам.
₁t	7 33,7	Основные Интерполяционные Таблицы
₂t		Для звёзд отсутствует.
t_ГР	280 42,4	Суммируем
Рассчитываем местный часовой угол т.		– 84 15.8	Долгота из условия +O^st -W
	196 26,6	Суммируем.Если результат больше 360º, 360 отбрасываем
Получаем местный часовой угол звезды		166 33,4	Звёздное дополнение. Таблица «Звёзды. Видимые места», левая сторона.
t_W	3º 00,0	Суммируем. Если результат меньше 180, оставляем в графе t_W, если больше – находим 360- t_W и заносим. в графу t_O.
t_O
Получаем склонение звезды.			Для звёзд не выбирается
_T

	55º 59,9 N	Склонение. Таблица «Звёзды. Видимые места», правая сторона

Источник

Как найти склонение звезды формула астрономия

Формула для вычисления склонения звезды

Как использовать склонение звезды

Итог

Как найти склонение звезды формула астрономия

Что такое склонение звезды?

Формула астрономии для нахождения склонения звезды

Шаги для использования формулы астрономии

Общий итог

Как найти склонение звезды

Используйте формулу для вычисления склонения

Как использовать формулу

Проверьте свои результаты

Заключение

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Упоминания в литературе (продолжение)

Описание[править | править код]

Суточное движение светил[править | править код]

Склонение Солнца[править | править код]

Влияние прецессии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как составить невербальный рассказ

Как найти кривую цена потребление

Как найти неизвестную координату точки

Добавить комментарий Отменить ответ