Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы
- Перпендикулярные прямые — определение и свойства
- Правила комбинаторики в задаче B6
- Метод координат в пространстве
- Четырехугольная пирамида: как найти координаты вершин
- Задача B4 про три дороги — стандартная задача на движение
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Геометрия
- Атанасян
- Задание 58
Условие
Найдите угол, смежный с углом ABC, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC= 15°.
Решение 1
Решение 2
Решение 3
Популярные решебники
-
Главная
-
ГДЗ
- 7 класс, 8 класс, 9 класс
- Геометрия
-
Атанасян учебник
- 58
Вернуться к содержанию учебника
Глава 1. Начальные геометрические сведения. Страница 24
53
54
55
56
57
58
59
60
61
62
63
Вопрос
Найдите угол, смежный с углом АВС, если: а) 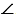
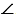
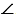
Подсказка
Вспомните:
- Что такое угол.
- Какие углы называются смежными и их свойство.
Ответ
53
54
55
56
57
58
59
60
61
62
63
53
54
55
56
57
58
59
60
61
62
63
Вернуться к содержанию учебника
Получи верный ответ на вопрос 🏆 «Найти Найдите угол смежный с углом ABC если угол ABC равен 111 градусам …» по предмету 📕 Геометрия, используя встроенную систему поиска. Наша обширная база готовых ответов поможет тебе получить необходимые сведения!
Найти готовые ответы
Главная » Геометрия » Найти Найдите угол смежный с углом ABC если угол ABC равен 111 градусам
Помогите решить задачу!!!!Очень надо,пожалуйста!!!!
Pa l Fos
Ученик
(141),
закрыт
14 лет назад
Как решить эту задачу????
Найдите угол смежный,с углом АВС если АВС=110 градусов.
Дополнен 14 лет назад
А то я ни фига не помню)))
Лучший ответ
Наталья
Гений
(63507)
14 лет назад
Смежными называются два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая) .
Т. е. смежный дополняет данный угол до 180 градусов, и равен 180-110=70 градусов
Остальные ответы
летающий кролик
Мастер
(1118)
14 лет назад
70 градусов
смежные углы в сумме дают 180 градусов – всё просто
Владимир Дмитриев
Ученик
(131)
14 лет назад
угол смежный с углом авс=180-110=70.
[LIEBER DEUTSCHE]
Знаток
(409)
14 лет назад
180-110=70градусов) ) элементарно))
Lena
Знаток
(331)
14 лет назад
это же легко!!!! сумма смежных углов равно 180градусов. 180-110=70градусов.




















