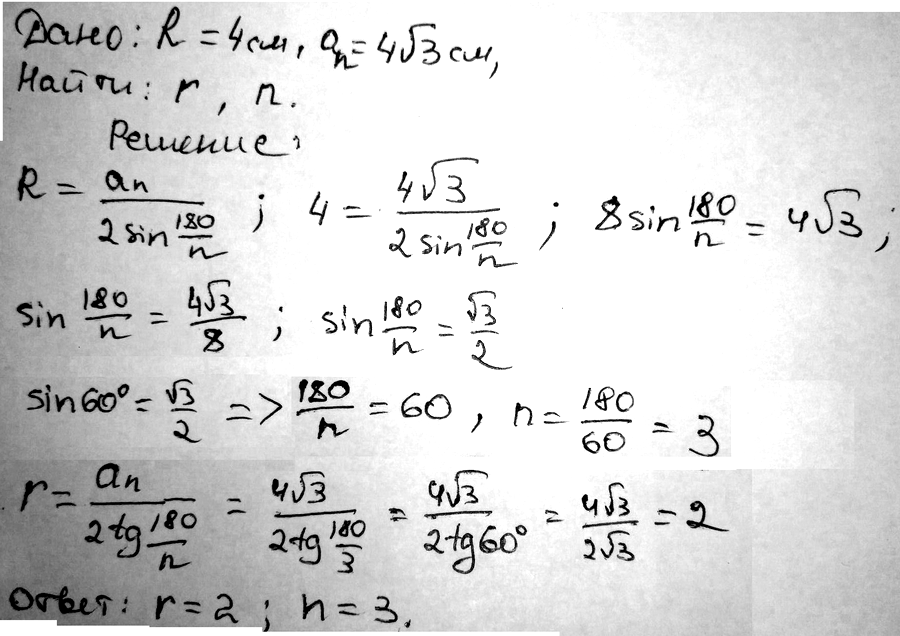Как найти угол сорокапятиугольника

Геометрия 9 Контрольная 2 (Мерзляк) с ответами. Контрольная работа по геометрии в 9 классе «Правильные многоугольники» для УМК Мерзляк, Полонский, Якир из 4-х вариантов. Методическое пособие для учителей и родителей.

Геометрия 9 класс (УМК Мерзляк)
Контрольная работа № 2

Тема: Правильные многоугольники

К-2 Вариант 1 (задания)

К-2 Вариант 2 (задания)

1. Найдите углы правильного сорокапятиугольника.
2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
3. Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата, вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника – 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 35° и 100°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.

К-2 Вариант 3 (задания)

1. Найдите углы правильного тридцатишестиугольника.
2. Найдите длину окружности, описанной около правильного треугольника со стороной 9 см.
3. В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности – 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.

К-2 Вариант 4 (задания)

1. Найдите углы правильного тридцатиугольника.
2. Найдите площадь круга, описанного около квадрата со стороной 16 см.
3. Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника, вписанного в эту окружность.
4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника – 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
5. Сторона треугольника равна 10√3 см, а прилежащие к ней углы равны 10° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
6. Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.

Ответы на контрольную работу № 2

ОТВЕТЫ на Вариант 1

№ 1. Найдите углы правильного сорокаугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 40 угол равен 180° × 38/40 = 171°.
ОТВЕТ: 171°.

№ 2. Найдите длину окружности, вписанной в правильный треугольник со стороной 12 см.
ОТВЕТ: 4π√3 см.

№ 3. В окружность вписан квадрат со стороной 8 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.
ОТВЕТ: (8√6)/3 см.

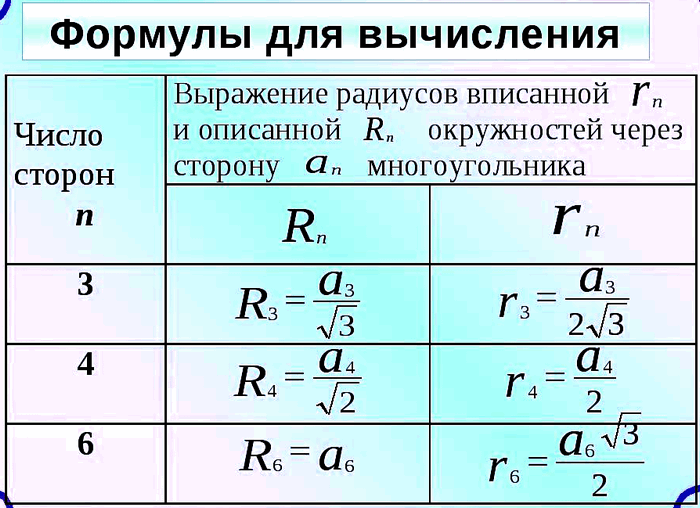
№ 4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника – 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.
ОТВЕТ: 1) 2 см;  2) 3 стороны.

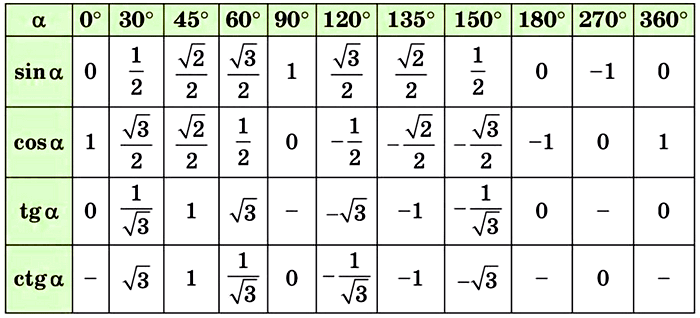
№ 5. Сторона треугольника равна 6√3 см, а прилежащие к ней углы равны 40° и 80°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 40 – 80 = 60⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 80⁰, 160⁰ и 120⁰.
Радиус описанной окр. R = (6√3) / (2 sin 60°) = (6√3) / (√3) = 6 см.
Длина всей окружности l = 2πR = 12π (см)
Дуги: (80/360)*12π = 8π/3 (см)
(160/360)*12π = 16π/3 (см)
(120/360)*12π = 4π (см) 
ОТВЕТ: 8π/3 см, 16π/3 см, 4π см.

№ 6. Углы правильного треугольника со стороной 6 см срезали так, что получили правильный шестиугольник. Найдите сторону образовавшегося шестиугольника.
ОТВЕТ:  2 см.
Подсказка: Так как отрезанные части углов — это тоже правильные треугольники, то их боковые стороны равны стороне правильного шестиугольника. Отсюда получаем, что сторона исходного треугольника разделена на 3 части. Следовательно, сторона образовавшегося шестиугольника равна 6/3 = 2 (см).

ОТВЕТЫ на Вариант 2

№ 1. Найдите углы правильного сорокапятиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 45 угол равен 180°×43/45 = 172°.
ОТВЕТ: 172°.

№ 2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.
ОТВЕТ: 75π см².

№ 3. Около окружности описан правильный треугольник со стороной 18 см. Найдите сторону квадрата, вписанного в эту окружность.
ОТВЕТ: 3√6 см.

№ 4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника – 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
Дано: r = 5 см; a_n = 10 см;
Найти: 1) R; 2) n – ?
Решение: 1) a_n = 2r tg (180°/n)
10 = 2 • 5 • tg (180°/n)  ⇒  1 = tg (180°/n).
По таблице находим 1 = tg 45°
==>  180°/n = 45°  ⇒  n = 4 (квадрат).
2) a_n = 2R sin (180°/n)
10 = 2R sin 45°  ⇒  R = 5/sin45° = 5•2/√2 = 5√2 (см).
ОТВЕТ: 1) 5√2 см;  2) 4 стороны.

№ 5. Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 35° и 100°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 100 – 35 = 45⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 90⁰, 70⁰ и 200⁰.
Радиус описанной окр. R = (8√2)/(2sin45⁰) = (8√2)/√2 = 8 (см)
Длина всей окружности l = 2πR = 16π (см)
Дуги: (90/360)*16π = 4π (см)
(70/360)*16π = 28π/9 (см)
(200/360)*16π = 80π/9 (см).
ОТВЕТ: 80π/9 см; 28π/9 см; 4π см.

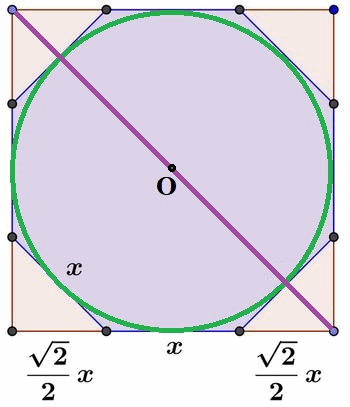
№ 6. Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону образовавшегося восьмиугольника.
ОТВЕТ: ≈ 3,3137 см.
Возможный вариант решения: Радиус вписанной окружности и для квадрата и для восьмиугольника = 4 см. Диагональ квадрата = 8√2 см. Половина диагонали квадрата (расстояние из центра вписанной окружности до угла квадрата) = 4√2 см. Срезанный уголок — это равнобедренный прямоугольный треугольник, высота которого = 4√2 — 4 (половина диагонали квадрата минус радиус окружности). Гипотенуза равнобедренного прямоугольного треугольника равна удвоенной высоте к гипотенузе, это и есть сторона образовавшегося восьмиугольника
х = 2 * (4√2 — 4) = 8√2 — 8 = 3,3137 (см)
Другой вариант решения: х = 8 / (√2 + 1) = 3,3137 (см) Смотри рисунок ниже.

ОТВЕТЫ на Вариант 3

№ 1. Найдите углы правильного тридцатишестиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 36 угол равен 180°×34/36 = 170°.
ОТВЕТ: 170°.

№ 2. Найдите длину окружности, описанной около правильного треугольника со стороной 9 см.
ОТВЕТ: 6π√3 см.

№ 3. В окружность вписан правильный шестиугольник со стороной 9 см. Найдите сторону правильного треугольника, описанного около этой окружности.
ОТВЕТ: 18√3 см.

№ 4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности – 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.
Дано: R = 8√2  см; r = 8 см;
Найти: 1) a_n; 2) n – ?
Решение: 1) r = R cos (180°/n)
8 = 8√2 cos (180°/n)  ⇒  cos (180°/n) = 8/8√2 = √2/2.
По таблице находим √2/2 = cos 45°
⇒  180°/n = 45°  ⇒  n = 4 (квадрат).
2) a_n = 2R sin (180°/n) = 2 • 8√2 • sin 45° = 16√2 • √2/2 = 16 (см).
ОТВЕТ: 1) 16 см;  2) 4 стороны.

№ 5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 45 – 105 = 30⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 90⁰, 210⁰ и 60⁰.
Радиус описанной окр. R = 5 / (2 sin 30°) = 5 / (2 • 1/2) = 5 см.
Длина всей окружности l = 2πR = 10π (см)
Дуги: (90/360)*10π = 2,5π (см)
(210/360)*10π = 35π/6 (см)
(60/360)*10π = 5π/3 (см)
ОТВЕТ: 2,5π см;  35π/6 см;  5π/3 см.

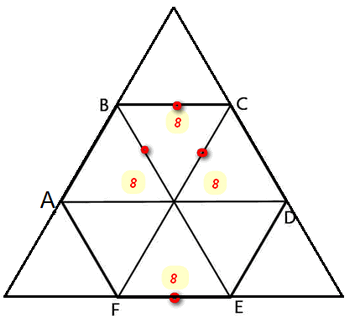
№ 6. Углы правильного треугольника срезали так, что получили правильный шестиугольник со стороной 8 см. Найдите сторону данного треугольника.
ОТВЕТ: 24 см.
Указание к решению: Проведем диагонали правильного шестиугольника ABCDEF, получим шесть РАВНОСТОРОННИХ треугольников (на чертеже отмечено). Диагональ правильного шестиугольника в два раза больше его стороны, т.е. 16 см. Срезанные углы треугольника тоже равносторонние треугольники. Следовательно сторона первоначального правильного треугольника равна 8 * 3 = 24 (см).

ОТВЕТЫ на Вариант 4

№ 1. Найдите углы правильного тридцатиугольника.
Решение: Сумма углов многоугольника равна 180°×(n-2). Так как у правильного многоугольника все углы равны, то величину угла можно вычислить как 180°×(n-2)/n. Для п = 30 угол равен 180°×28/30 = 168°.
ОТВЕТ: 168°.

№ 2. Найдите площадь круга, описанного около квадрата со стороной 16 см.
Решение: S = R²π. R = d/2 = a√2/2.
S = (16√2/2)²π = (8√2)²π = 8²*2π = 2*64π = 128π (см²)
ОТВЕТ: 128π см².

№ 3. Около окружности описан квадрат со стороной 36 см. Найдите сторону правильного треугольника, вписанного в эту окружность.
Решение: Радиус вписанной в квадрат окружности R = 36 : 2 = 18(см). Это же радиус описанной окружности около треугольника. Сторону правильного треугольника находим по формуле а = R√3 = 18√3 (см).

ОТВЕТ: 18√3 см.

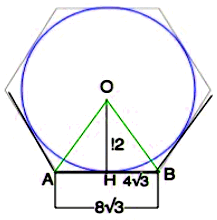
№ 4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника – 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.
Решение: Центр вписанной в угол окружности лежит на биссектрисе.
Окружности, вписанной в правильный многоугольник — в точке пересечения биссектрис его углов. На рисунке АВ — сторона, АО = ВО — биссектрисы углов правильного многоугольника. ОН — радиус вписанной окружности,
tg∠ОВН = ОН : ВН = √3.
Следовательно, ∠ОВН = 60°, угол многоугольника 120°, смежный с ним внешний угол равен 60°. Сумма внешних углов многоугольника 360°. Количество внешних углов, взятых по одному при вершинах, равно числу сторон многоугольника.
Число сторон 360° : 60° = 6.
Радиус описанной около правильного шестиугольника окружности равен его стороне R₆ = a₆ = 8√3.

ОТВЕТ: 1) 8√3 см;  2) 6 сторон.

№ 5. Сторона треугольника равна 10√3 см, а прилежащие к ней углы равны 10° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.
Решение: Третий угол = 180 – 10 – 50 = 120⁰. Вписанные углы равны половине дуг, на которые они опираются, т.е. 20⁰, 100⁰ и 240⁰.
Радиус описанной окр. R = 10√3 / (2 sin 120°) = 10√3 / √3 = 10 см.
Длина всей окружности l = 2πR = 20π (см)
Дуги: (20/360) • 20π = 10π/9 (см)
(100/360) • 20π = 50π/9 (см)
(240/360) • 20π = 40π/3 (см).
ОТВЕТ: 10π/9 см; 50π/9 см; 40π/3 см.

№ 6. Углы квадрата срезали так, что получили правильный восьмиугольник со стороной 4 см. Найдите сторону данного квадрата.
ОТВЕТ:  4 (√2 + 1) ≈ 9,67 см.

Вы смотрели: Геометрия 9 Контрольная 2 (Мерзляк). Контрольная работа по геометрии в 9 классе «Решение треугольников» для УМК Мерзляк, Полонский, Якир в 4-х вариантах. Методическое пособие.

Смотреть аналогичную контрольную № 2 с решениями (2 варианта)

Вернуться к Списку контрольных работ из Методички (по 4 варианта)

Цитаты из пособия «Геометрия 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.