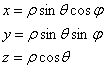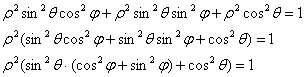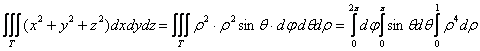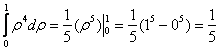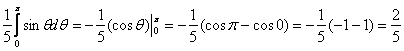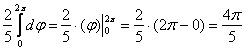Как найти угол тета

В математике изучение треугольников называется тригонометрией. Любые неизвестные значения углов и сторон могут быть обнаружены с использованием общих тригонометрических тождеств синуса, косинуса и тангенса. Эти тождества представляют собой простые вычисления, используемые для преобразования отношения сторон в градусы угла. Неизвестные углы обозначаются как угол тета и может быть рассчитан различными способами на основе известных сторон и углов.

Правые треугольники

Когда треугольник содержит угол 90 градусов, он известен как прямоугольный треугольник, а угол тета можно определить с помощью аббревиатуры SOHCAHTOA.

В разбивке это означает, что синус (S) равен длине стороны противоположного угла тета (O), деленной на длину гипотенузы (H), так что Sin (X) = Opp / Hyp. Точно так же косинус (C) равен длине смежной стороны (A), деленной на гипотенузу. (H) Cos (X) = Adj / Hyp. Касательная (T) равна противоположной (O), деленной на соседнюю (A). Желто-коричневый (X) = Opp / Adj.

Если длина противоположной стороны известна так же, как и гипотенуза – соответствует SOH в аббревиатуру – используйте функцию arcsin на калькуляторе, а затем введите две длины в дробном форма.

Например: если сторона, противоположная углу тета, имеет длину 4, а гипотенуза – 5, введите соотношение в калькулятор следующим образом:

SIN ^ -1 (4/5)

Это должно вывести значение примерно 53,13 градуса. Если нет, убедитесь, что калькулятор установлен в режим СТЕПЕНИ, а затем повторите попытку.

Закон синуса

Если в треугольнике нет углов в 90 градусов, SOHCAHTOA не имеет значения при вычислении углов. Однако, если известны угол и длина его противоположной стороны, Закон синуса может использоваться совместно с другой известной длиной стороны для поиска недостающих углов. Закон гласит, что sin A / a = sin B / b = sin C / c.

В разрезе это означает, что синус угла, деленный на длину его противоположной стороны, прямо пропорционален синусу другого угла, деленному на длину его противоположной стороны. Чтобы решить, выделите синус неизвестного угла, умножив обе части уравнения на длину противоположной стороны угла тета.

Например: sin A / a = sin B / b становится (b * sin A) / a = sin B

В калькуляторе для данной стороны a = 5, b = 7 и угла A = 45 градусов это отображается как SIN ^ -1 ((7 * SIN (45)) / 5). Это дает значение угла B приблизительно 81,87 градуса.

Закон косинусов

В Закон косинусов работает для всех треугольников, но в основном используется в тех случаях, когда известны длины всех сторон, но не известен ни один из углов. Формула аналогична формуле Теорема Пифагора (a ^ 2 + b ^ 2 = c ^ 2) и состояния c ^ 2 = a ^ 2 + b ^ 2 – 2ab * cos (C). Но для определения теты ее легче читать как cos (C) = (a ^ 2 + b ^ 2 – c ^ 2) / 2ab.

Например, если у треугольника есть три стороны размером 5, 7 и 10, введите эти значения в графический калькулятор как cos ^ -1 ((5 ^ 2 + 7 ^ 2-10 ^ 2) / (2_5_7)). Этот расчет дает значение приблизительно 111,80 градусов.

Практика для мастерства

Важно помнить, что все треугольники состоят из трех углов, общая сумма которых составляет 180 градусов. Практикуйте разные техники на разных треугольниках, пока процесс не станет привычным. Иногда открытие тэты – это то же самое, что открытие нового способа решения проблемы.

Содержание

• Образец вопроса
• Вопросы практики

Если вам заданы векторные компоненты, такие как (3, 4), вы можете легко преобразовать их в способ выражения векторов по амплитуде / углу, используя тригонометрию.

Например, взгляните на вектор на изображении.

Предположим, что вы дали координаты конца вектора и хотите найти его величину, vи угол тета. Из-за ваших знаний тригонометрии, вы знаете,

Где загар тетатангенс угла. Это означает, что

тета = загар^–1(Y/Икс)

Предположим, что координаты вектора (3, 4). Вы можете найти угол тета как загар^–1(4/3) = 53 градуса.

Вы можете использовать теорему Пифагора, чтобы найти гипотенуза – величина, v – треугольника, образованного х, у, и v:

Вставьте цифры для этого примера, чтобы получить

Поэтому, если у вас есть вектор, заданный координатами (3, 4), его величина равна 5, а угол составляет 53 градуса.

Образец вопроса

1. Преобразовать вектор, заданный координатами (1.0, 5.0), в формат величины / угла.

   Правильный ответ – величина 5,1, угол 79 градусов.

   1. Примените теорему Пифагора, чтобы найти величину. Вставьте цифры, чтобы получить 5.1.

   2. Применим уравнение тета = загар^–1(Y/Икс) чтобы найти угол. Вставьте цифры, чтобы получить загар^–1(5,0 / 1,0) = 79 градусов.

Вопросы практики

1. Преобразуйте вектор (5.0, 7.0) в форму величины / угла.

2. Преобразуйте вектор (13,0, 13,0) в форму величины / угла.

3. Преобразовать вектор (–1,0, 1,0) в форму величины / угла.

4. Преобразуйте вектор (–5,0, –7,0) в форму величины / угла.

Ниже приведены ответы на практические вопросы:

1. Величина 8,6, угол 54 градуса

   1. Применить уравнение

      

   найти величину, которая составляет 8,6.

   1. Применим уравнение тета = загар^–1(Y/Икс) чтобы найти угол: загар^–1(7,0 / 5,0) = 54 градуса.

2. Величина 18,4, угол 45 градусов

   1. Применить уравнение

      

      найти величину, которая составляет 18,4.

   2. Применим уравнение тета = загар^–1(Y/Икс) чтобы найти угол: загар^–1(13,0 / 13,0) = 45 градусов.

3. Величина 1,4, угол 135 градусов

   1. Применить уравнение

      

      найти величину, которая составляет 1,4.

   2. Применим уравнение тета = загар^–1(Y/Икс) чтобы найти угол: загар^–1(1,0 / –1,0) = –45 градусов.

      Тем не менее, обратите внимание, что угол действительно должен быть между 90 и 180 градусами, потому что первый компонент вектора отрицателен, а второй положителен. Это означает, что вы должны добавить 180 градусов к –45 градусам, что даст вам 135 градусов (тангенс 135 градусов также равен 1,0 / –1,0 = –1,0).

4. Величина 8,6, угол 234 градуса

   1. Применить уравнение

      

      найти величину, которая составляет 8,6.

   2. Примените уравнение theta = tan – 1 (y / x), чтобы найти угол: tan – 1 (–7,0 / –5,0) = 54 градуса.

      Тем не менее, обратите внимание, что угол действительно должен быть между 180 и 270 градусами, потому что оба компонента вектора отрицательны. Это означает, что вы должны добавить 180 градусов к 54 градусам, что дает вам 234 градуса (тангенс 234 градусов также равен –7.0 / –5.0 = 7.0 / 5.0).

В Углы Эйлера – это три угла, представленные Леонард Эйлер описать ориентация из жесткое тело относительно фиксированного система координат.^[1]

Они также могут отображать ориентацию мобильного точка зрения в физике или ориентация на общую основа в 3-х мерный линейная алгебра. Альтернативные формы были позже введены Питер Гатри Тейт и Джордж Х. Брайан предназначен для использования в авиастроении и технике.

Эквивалентность цепных вращений

Углы Эйлера могут быть определены элементарным геометрия или по составу вращений. Геометрическое определение показывает, что три составленных элементарные вращения (вращения вокруг осей система координат ) всегда достаточно для достижения любого целевого кадра.

Три вращения элементов могут быть внешний (вращения вокруг осей xyz исходной системы координат, которая предполагается неподвижной), или внутренний (вращения вокруг осей вращающейся системы координат XYZ, солидарен с движущимся телом, меняющим ориентацию после каждого элементарного вращения).

Углы Эйлера обычно обозначают как α, β, γ, или же ψ, θ, φ. Разные авторы могут использовать разные наборы осей вращения для определения углов Эйлера или разные имена для одних и тех же углов. Следовательно, любому обсуждению, использующему углы Эйлера, всегда должно предшествовать их определение.

Без учета возможности использования двух различных соглашений для определения осей вращения (внутренней или внешней) существует двенадцать возможных последовательностей осей вращения, разделенных на две группы:

• Правильные углы Эйлера (z–Икс–z, Икс–у–Икс, у–z–у, z–у–z, Икс–z–Икс, у–Икс–у)
• Углы Тейта – Брайана (Икс–у–z, у–z–Икс, z–Икс–у, Икс–z–у, z–у–Икс, у–Икс–z).

Углы Тейта – Брайана также называют Углы кардана; морские углы; Заголовок, высота и берег; или же рыскание, тангаж и крен. Иногда оба вида последовательностей называют «углами Эйлера». В этом случае последовательности первой группы называются правильный или же классический Углы Эйлера.

Правильные углы Эйлера

Геометрическое определение

Оси исходного кадра обозначены как Икс, у, z а оси повернутой рамы – как Икс, Y, Z. В геометрическое определение (иногда называемый статическим) начинается с определения линия узлов (N) как пересечение плоскостей ху и XY (его также можно определить как общий перпендикуляр к осям z и Z а затем записывается как векторное произведение N = z Z). Используя его, три Углы Эйлера можно определить следующим образом:

Углы Эйлера между двумя опорными кадрами определяются только в том случае, если оба кадра имеют одинаковые руки.

Соглашения по внутреннему вращению

Внутренние вращения – это элементарные вращения, которые происходят вокруг осей системы координат. XYZ прикреплен к движущемуся телу. Следовательно, они меняют свою ориентацию после каждого вращения элемента. В XYZ система вращается, а xyz фиксированный. Начиная с XYZ перекрытие xyz, композиция из трех собственных вращений может использоваться для достижения любой целевой ориентации для XYZ.

Углы Эйлера могут быть определены внутренними вращениями. Повернутая рама XYZ можно представить, что изначально он был согласован с xyz, прежде чем претерпеть три элементарных вращения, представленных углами Эйлера. Его последовательные ориентации можно обозначить следующим образом:

• Икс–у–z, или же Икс₀–у₀–z₀ (исходный)
• Икс′-у′-z‘, или же Икс₁–у₁–z₁ (после первого вращения)
• Икс″-у″-z“, или же Икс₂–у₂–z₂ (после второго вращения)
• Икс–Y–Z, или же Икс₃–у₃–z₃ (окончательный)

Для указанной выше последовательности поворотов линия узлов N можно просто определить как ориентацию Икс после первого вращения элементаля. Следовательно, N можно просто обозначить Икс′. Более того, поскольку третье вращение элемента происходит около Z, это не меняет ориентацию Z. Следовательно Z совпадает с z″. Это позволяет упростить определение углов Эйлера следующим образом:

Соглашения по внешнему вращению

Внешние вращения – это элементарные вращения, которые происходят вокруг осей фиксированной системы координат. xyz. В XYZ система вращается, а xyz фиксированный. Начиная с XYZ перекрытие xyz, композиция из трех внешних вращений может быть использована для достижения любой целевой ориентации для XYZ. Углы Эйлера или Тейта – Брайана (α, β, γ) – амплитуды этих вращений элементов. Например, целевая ориентация может быть достигнута следующим образом (обратите внимание на обратный порядок приложения угла Эйлера):

• В XYZ система вращается вокруг z ось γ. В Икс ось теперь под углом γ с уважением к Икс ось.
• В XYZ система снова вращается вокруг Икс ось β. В Z ось теперь под углом β с уважением к z ось.
• В XYZ система вращается в третий раз вокруг z ось α.

В общем, три вращения элементов происходят примерно на z, Икс и z. Действительно, эту последовательность часто обозначают z–Икс–z (или 3-1-3). Наборы осей вращения, связанные как с собственными углами Эйлера, так и с углами Тейта – Брайана, обычно называются с использованием этой нотации (подробности см. Выше).

Знаки, диапазоны и условные обозначения

Углы обычно определяются в соответствии с правило правой руки. А именно, они имеют положительные значения, когда они представляют собой вращение по часовой стрелке, если смотреть в положительном направлении оси, и отрицательные значения, когда вращение появляется против часовой стрелки. Противоположное соглашение (правило левой руки) применяется реже.

О диапазонах (используя обозначение интервалов ):

• за α и γ, диапазон определяется по модулю 2π радианы. Например, допустимый диапазон может быть [−π, π].
• за β, ассортимент охватывает π радианы (но нельзя сказать, что они по модулюπ). Например, это могло быть [0, π] или же [−π/2, π/2].

Углы α, β и γ определены однозначно, за исключением особого случая, когда ху и XY самолеты идентичны, т.е. когда z ось и Z оси имеют одинаковое или противоположное направление. Действительно, если z ось и Z оси такие же, β = 0 и только (α + γ) однозначно определено (а не отдельные значения), и, аналогично, если z ось и Z оси противоположны, β = π и только (α − γ) однозначно определено (а не отдельные значения). Эти двусмысленности известны как карданный замок в приложениях.

Есть шесть возможностей выбора осей вращения для собственных углов Эйлера. Во всех них первая и третья оси вращения совпадают. Шесть возможных последовательностей:

1. z₁–Икс′-z₂″ (Собственное вращение) или z₂–Икс–z₁ (внешние вращения)
2. Икс₁–у′-Икс₂″ (Собственное вращение) или Икс₂–у–Икс₁ (внешние вращения)
3. у₁–z′-у₂″ (Собственное вращение) или у₂–z–у₁ (внешние вращения)
4. z₁–у′-z₂″ (Собственное вращение) или z₂–у–z₁ (внешние вращения)
5. Икс₁–z′-Икс₂″ (Собственное вращение) или Икс₂–z–Икс₁ (внешние вращения)
6. у₁–Икс′-у₂″ (Собственное вращение) или у₂–Икс–у₁ (внешние вращения)

Прецессия, нутация и собственное вращение

Прецессия, нутация, и собственное вращение (вращение) определяются как движения, полученные путем изменения одного из углов Эйлера, оставляя два других постоянными. Эти движения выражаются не в терминах внешней рамы или в терминах совместно движущейся вращающейся рамы тела, а в виде смеси. Они составляют смешанные оси вращения система, в которой первый угол перемещает линию узлов вокруг внешней оси z, второй вращается вокруг линии узлов N а третий – внутреннее вращение вокруг Z, ось, закрепленная в движущемся теле.

Статическое определение подразумевает, что:

• α (прецессия) представляет собой вращение вокруг z ось,
• β (нутация) представляет собой вращение вокруг N или ось x ′,
• γ (внутреннее вращение) представляет собой вращение вокруг Z или ось z ″.

Если β равен нулю, вращения вокруг N. Как следствие, Z совпадает с z, α и γ представляют повороты вокруг одной оси (z), а окончательная ориентация может быть получена одним поворотом вокруг z, на угол, равный α + γ.

В качестве примера рассмотрим верх. Вершина вращается вокруг своей оси симметрии; это соответствует его собственному вращению. Он также вращается вокруг своей оси вращения, а его центр масс вращается вокруг оси вращения; это вращение – прецессия. Наконец, верх может раскачиваться вверх и вниз; угол наклона – это угол нутации. Тот же пример можно увидеть с движениями Земли.

Хотя все три движения могут быть представлены оператором вращения с постоянными коэффициентами в некоторой системе отсчета, они не могут быть представлены этими операторами одновременно. При заданной системе отсчета максимум одна из них будет без коэффициентов. Только прецессия может быть выражена в общем виде в виде матрицы в основе пространства без зависимостей других углов.

Эти движения также действуют как карданный подвес. Если мы предположим набор кадров, каждый из которых может перемещаться по отношению к предыдущему только под одним углом, как у подвеса, будет существовать внешний фиксированный кадр, один последний кадр и два кадра посередине, которые называются «промежуточными». кадры ». Два в середине работают как два карданных кольца, которые позволяют последней рамке достигать любой ориентации в пространстве.

Углы Тейта – Брайана

Второй тип формализма называется Углы Тейта – Брайана, после Питер Гатри Тейт и Джордж Х. Брайан. Это соглашение, обычно используемое для аэрокосмических приложений, так что нулевой угол места соответствует горизонтальному положению. Углы Тейта-Брайана представляют ориентацию самолета относительно мировой системы координат. При работе с другими транспортными средствами разные топоры соглашения возможны.

Определения

Определения и обозначения, используемые для углов Тейта – Брайана, аналогичны описанным выше для собственных углов Эйлера (геометрическое определение, определение внутреннего вращения, определение внешнего вращения ). Единственное отличие состоит в том, что углы Тейта – Брайана представляют собой вращения вокруг трех различных осей (например, Икс–у–z, или же Икс–у′-z″), В то время как правильные углы Эйлера используют одну и ту же ось как для первого, так и для третьего вращения элемента (например, z–Икс–z, или же z–Икс′-z″).

Отсюда следует другое определение линия узлов в геометрической конструкции. В случае собственных углов Эйлера это было определено как пересечение двух гомологичных декартовых плоскостей (параллельных, когда углы Эйлера равны нулю; например, ху и XY). В случае углов Тейта-Брайана он определяется как пересечение двух негомологических плоскостей (перпендикулярных, когда углы Эйлера равны нулю; например, ху и YZ).

Конвенции

Три вращения элемента могут происходить либо вокруг осей исходной системы координат, которая остается неподвижной (внешние вращения ), или вокруг осей вращающейся системы координат, которая меняет свою ориентацию после каждого элементарного вращения (собственное вращение ).

Есть шесть возможностей выбора осей вращения для углов Тейта – Брайана. Шесть возможных последовательностей:

• Икс–у′-z″ (Собственное вращение) или z–у–Икс (внешние вращения)
• у–z′-Икс″ (Собственное вращение) или Икс–z–у (внешние вращения)
• z–Икс’–у″ (Собственное вращение) или у–Икс–z (внешние вращения)
• Икс–z′-у″ (Собственное вращение) или у–z–Икс (внешние вращения)
• z–у′-Икс″ (Собственное вращение) или Икс–у–z (внешние вращения): внутренние вращения известны как рыскание, тангаж и крен
• у–Икс′-z″ (Собственное вращение) или z–Икс–у (внешние вращения)

Знаки и диапазоны

Соглашение Тейта – Брайана широко используется в инженерии с разными целями. Есть несколько топоры соглашения на практике для выбора подвижных и неподвижных осей, и эти условности определяют знаки углов. Поэтому знаки необходимо изучать в каждом конкретном случае внимательно.

Диапазон углов ψ и φ обложки 2π радианы. За θ ассортимент охватывает π радианы.

Альтернативные названия

Эти углы обычно принимаются равными единице во внешней системе отсчета (Заголовок, несущий ), одна в собственной подвижной системе отсчета (банк ) и один в средней рамке, представляющий высота или наклон по отношению к горизонтальной плоскости, что для этой цели эквивалентно линии узлов.

Для самолета их можно получить за три оборота вокруг своей оси. главные оси если все сделано в правильном порядке. А рыскание получит подшипник, подача даст высоту, а крен дает угол крена. Поэтому в авиакосмической сфере их иногда называют рыскание, тангаж и крен. Обратите внимание, что это не будет работать, если повороты применяются в любом другом порядке, или если оси самолета начать в любом положении, не эквивалентна системе отсчета.

Углы Тейта – Брайана, следующие z–у′-Икс″ (Внутреннее вращение), также известное как морские углы, потому что они могут использоваться для описания ориентации корабля или самолета, или Углы кардана, в честь итальянского математика и физика Джероламо Кардано, который впервые подробно описал Карданная подвеска и Карданный шарнир.

Углы данного кадра

Распространенная проблема – найти углы Эйлера заданного кадра. Самый быстрый способ получить их – записать три заданных вектора в виде столбцов матрицы и сравнить их с выражением теоретической матрицы (см. Таблицу матриц ниже). Следовательно, можно вычислить три угла Эйлера. Тем не менее, того же результата можно достичь, избегая матричной алгебры и используя только элементарную геометрию. Здесь мы представляем результаты для двух наиболее часто используемых соглашений: ZXZ для собственных углов Эйлера и ZYX для Tait – Bryan. Обратите внимание, что любое другое соглашение можно получить, просто изменив имя осей.

Правильные углы Эйлера

Предполагая кадр с единичные векторы (Икс, Y, Z), заданные их координатами, как на основной диаграмме, можно увидеть, что:

И с тех пор

за у нас есть

В качестве – двойная проекция унитарного вектора,

Аналогичная конструкция существует для , сначала проецируя его на плоскость, определяемую осью z и линия узлов. Поскольку угол между плоскостями равен и , это ведет к:

и наконец, используя обратный косинус функция

Углы Тейта – Брайана

Предполагая кадр с единичные векторы (Икс, Y, Z), заданные их координатами, как на этой новой диаграмме (обратите внимание, что угол тета отрицательный), можно увидеть, что:

Как прежде,

за у нас есть

аналогично предыдущему:

Ищем выражения, похожие на предыдущие:

Обратите внимание, что функции обратного синуса и косинуса дают два возможных значения аргумента. В этом геометрическом описании действительно только одно из решений. Когда углы Эйлера определены как последовательность поворотов, все решения могут быть действительными, но внутри диапазонов углов будет только одно. Это связано с тем, что последовательность поворотов для достижения целевого кадра не уникальна, если диапазоны не определены ранее.^[2]

Для вычислительных целей может быть полезно представить углы с помощью atan2 (у, Икс). Например, в случае правильных углов Эйлера:

Преобразование в другие представления ориентации

Углы Эйлера – это один из способов представления ориентации. Есть и другие, и их можно изменить на другие соглашения. Всегда требуются три параметра для описания ориентации в 3-х мерный Евклидово пространство. Их можно задавать несколькими способами, в том числе углы Эйлера; видеть графики на SO (3) для других.

Наиболее часто используемым представлением ориентации являются матрицы вращения, то ось-угол и кватернионы, также известный как Параметры Эйлера – Родригеса, которые обеспечивают другой механизм для представления трехмерных вращений. Это эквивалентно описанию специальной унитарной группы.

Выражение вращений в 3D в виде единичных кватернионов вместо матриц имеет некоторые преимущества:

• Объединение поворотов в вычислительном отношении быстрее и численно более стабильно.
• Выделить угол и ось вращения проще.
• Интерполяция более проста. См. Например Slerp.
• Кватернионы не страдают карданный замок как это делают углы Эйлера.

В любом случае вычисление матрицы вращения – это первый шаг для получения двух других представлений.

Матрица вращения

Любая ориентация может быть достигнута путем составления трех элементарных вращений, начиная с известной стандартной ориентации. Равнозначно любой матрица вращения р возможно разложенный как продукт трех элементарных матриц вращения. Например:

матрица вращения, которая может использоваться для представления композиции внешние вращения о топорах z, у, Икс, (в таком порядке), или состав собственное вращение о топорах Икс–у′-z” (в этой последовательности). Однако оба определения матриц вращения элементов Икс, Y, Z, и порядок их умножения зависят от выбора, сделанного пользователем в отношении определения как матриц вращения, так и углов Эйлера (см., например, Неоднозначности в определении матриц вращения ). К сожалению, разные наборы соглашений принимаются пользователями в разных контекстах. Следующая таблица была построена в соответствии с этим набором соглашений:

1. Каждая матрица предназначена для работы путем предварительного умножения вектор-столбец (видеть Неоднозначности в определении матриц вращения )
2. Каждая матрица предназначена для представления активное вращение (составляющая и составная матрицы должны воздействовать на координаты векторов, определенных в исходной фиксированной системе отсчета, и давать в результате координаты повернутого вектора, определенного в той же системе отсчета).
3. Каждая матрица предназначена для представления, в первую очередь, состава внешние вращения (что соответствует конструктивной оценке матрицы R путем умножения трех истинно элементарных матриц) и, во-вторых, составу трех неэлементных матриц, представляющих глобально собственное вращение (вокруг осей вращающейся системы отсчета в обратном порядке).
4. Правша системы отсчета принимаются, и правило правой руки используется для определения знака углов α, β, γ.

Для простоты в следующей таблице матричных продуктов используется следующая номенклатура:

1. 1, 2, 3 обозначают углы α, β и γ, то есть углы, соответствующие поворотам первого, второго и третьего элемента соответственно.
2. Икс, Y, Z матрицы, представляющие вращения элементов вокруг осей Икс, у, z фиксированной рамы (например, Икс₁ представляет собой вращение вокруг Икс под углом α).
3. s и c представляют синус и косинус (например, s₁ представляет собой синус α).

Правильные углы Эйлера	Углы Тейта – Брайана

^[3]

Чтобы изменить формулы для пассивные вращения (или найти обратное активное вращение), транспонировать матрицы (затем каждая матрица преобразует начальные координаты вектора, остающегося фиксированным, в координаты того же вектора, измеренного в повернутой системе отсчета; та же ось вращения, те же углы, но теперь система координат вращается, а не вектор).

Характеристики

Углы Эйлера образуют Диаграмма на всех ТАК (3), то специальная ортогональная группа вращений в трехмерном пространстве. График гладкий, за исключением сингулярности в стиле полярных координат вдоль β = 0. Видеть графики на SO (3) для более полного лечения.

Пространство вращений в общем называется “The Гиперсфера вращений “, хотя это неправильное название: группа Отжим (3) является изометрический в гиперсферу S³, но пространство вращения SO (3) вместо этого изометрично реальное проективное пространство RP³ что является 2-кратным факторное пространство гиперсферы. Эта двусмысленность 2 к 1 является математическим происхождением вращение в физике.

Аналогичное разложение по трем углам применяется к SU (2), то особая унитарная группа вращений в сложном 2D-пространстве, с той разницей, что β варьируется от 0 до & nsbp2π. Их также называют углами Эйлера.

В Мера Хаара для SO (3) в углах Эйлера задается параметризацией углов Хопфа для SO (3), ,^[4] куда параметриз , пространство осей вращения.

Например, чтобы генерировать равномерно рандомизированные ориентации, пусть α и γ быть равномерным от 0 до 2π, позволять z равномерно от −1 до 1, и пусть β = arccos (z).

Геометрическая алгебра

Другие свойства углов Эйлера и поворотов в целом можно найти из геометрическая алгебра, абстракция более высокого уровня, в которой кватернионы являются четной подалгеброй. Основным инструментом геометрической алгебры является ротор куда угол поворота, ось вращения (унитарный вектор) и псевдоскалярный (тривектор в )

Высшие измерения

Можно определить параметры, аналогичные углам Эйлера, в размерностях больше трех.^[5]

Число степеней свободы матрицы вращения всегда меньше квадрата размерности матрицы. То есть не все элементы матрицы вращения полностью независимы. Например, матрица вращения в размерности 2 имеет только одну степень свободы, поскольку все четыре ее элемента зависят от одного угла поворота. Матрица вращения в размерности 3 (которая имеет девять элементов) имеет три степени свободы, соответствующие каждому независимому вращению, например, по ее трем углам Эйлера или кватерниону величиной один (единичный).

В ТАК (4) матрица вращения определяется двумя кватернионами, и поэтому является 6-параметрическим (три степени свободы для каждого кватерниона). В 4×4 Таким образом, матрицы вращения имеют 6 из 16 независимых компонентов.

Любой набор из 6 параметров, определяющих матрицу вращения, можно рассматривать как расширение углов Эйлера до измерения 4.

В общем, количество углов Эйлера в размерности D квадратично по D; поскольку любое вращение состоит из выбора двух измерений для вращения, общее количество поворотов, доступных в измерении является , который для дает .

Приложения

Транспортные средства и движущиеся рамы

Их главное преимущество перед другими описаниями ориентации состоит в том, что их можно напрямую измерить с подвеса, установленного в транспортном средстве. Поскольку гироскопы поддерживают постоянную ось вращения, углы, измеренные в корпусе гироскопа, эквивалентны углам, измеренным в лабораторном корпусе. Следовательно, гироскопы используются для определения фактической ориентации движущегося космического корабля, а углы Эйлера можно измерить напрямую. Собственный угол поворота невозможно определить с одного подвеса, поэтому в космическом корабле должно быть более одного подвеса. Обычно для резервирования используется как минимум три. Также есть отношение к хорошо известным карданный замок проблема машиностроение ^[6] .

Изучая твердые тела в целом, мы называем xyz система космические координаты, а XYZ система координаты тела. Пространственные координаты считаются неподвижными, в то время как координаты тела считаются вложенными в движущееся тело. Расчеты с участием ускорение, угловое ускорение, угловая скорость, угловой момент, и кинетическая энергия часто проще всего в телесных координатах, потому что тогда тензор момента инерции не меняется во времени. Если также диагонализовать тензор момента инерции твердого тела (с девятью компонентами, шесть из которых независимы), то получится набор координат (называемых главными осями), в котором тензор момента инерции имеет только три компонента.

Угловая скорость твердого тела равна простая форма с использованием углов Эйлера в подвижной системе отсчета. Так же Уравнения твердого тела Эйлера проще, потому что тензор инерции постоянен в этой системе отсчета.

Кристаллографическая текстура

В материаловедении, кристаллографическом текстура (или предпочтительную ориентацию) можно описать с помощью углов Эйлера. В текстурном анализе углы Эйлера обеспечивают математическое описание ориентации отдельных кристаллитов в поликристаллическом материале, что позволяет количественно описать макроскопический материал.^[8] Наиболее распространенное определение углов принадлежит Бунге и соответствует ZXZ соглашение. Однако важно отметить, что приложение обычно включает в себя преобразования осей тензорных величин, то есть пассивные вращения. Таким образом, матрица, соответствующая углам Бунге-Эйлера, является транспонированной матрицей, показанной в таблице выше.^[9]

Другие

Углы Эйлера, обычно в соглашении Тейта – Брайана, также используются в робототехника за то, что говорят о степенях свободы запястье. Они также используются в электронный контроль устойчивости Аналогичным образом.

Системы управления огнем орудия требуют корректировки углов расположения орудий (пеленг и возвышение), чтобы компенсировать наклон палубы (тангаж и крен). В традиционных системах стабилизирующий гироскоп с вертикальной осью вращения корректирует наклон палубы и стабилизирует оптические прицелы и антенну радара. Однако стволы орудия указывают в направлении, отличном от линии визирования цели, чтобы предвидеть движение цели и падение снаряда под действием силы тяжести, среди других факторов. Артиллерийские установки катятся и наклоняются вместе с плоскостью палубы, но также требуют стабилизации. Порядок пушки включает углы, вычисленные из данных вертикального гироскопа, и эти вычисления включают углы Эйлера.

Углы Эйлера также широко используются в квантовой механике углового момента. В квантовой механике явное описание представлений SO (3) очень важно для вычислений, и почти вся работа была проделана с использованием углов Эйлера. В ранней истории квантовой механики, когда физики и химики резко отрицательно относились к абстрактным теоретико-групповым методам (так называемым Группенпест), опора на углы Эйлера также была необходима для фундаментальной теоретической работы.

Многие мобильные вычислительные устройства содержат акселерометры которые могут определять углы Эйлера этих устройств относительно гравитационного притяжения Земли. Они используются в таких приложениях, как игры, пузырьковый уровень симуляции и калейдоскопы.^{[нужна цитата ]}

Смотрите также

• 3D проекция
• Ось-угол представления
• Преобразование кватернионов в углы Эйлера
• Цепные вращения Давенпорта
• Теорема Эйлера вращения
• Карданный замок
• Кватернион
• Кватернионы и пространственное вращение
• Формализмы вращения в трех измерениях
• Сферическая система координат

Рекомендации

Библиография

• Biedenharn, L.C .; Лук, Дж. Д. (1981), Угловой момент в квантовой физике, Ридинг, Массачусетс: Эддисон – Уэсли, ISBN  978-0-201-13507-7
• Гольдштейн, Герберт (1980), Классическая механика (2-е изд.), Рединг, Массачусетс: Аддисон – Уэсли, ISBN  978-0-201-02918-5
• Грей, Эндрю (1918), Трактат о гиростатике и вращательном движении, Лондон: Macmillan (опубликовано в 2007 г.), ISBN  978-1-4212-5592-7
• Роуз, М. Э. (1957), Элементарная теория углового момента, Нью-Йорк, Нью-Йорк: Джон Уайли и сыновья (опубликовано в 1995 г.), ISBN  978-0-486-68480-2
• Саймон, Кейт (1971), Механика, Ридинг, Массачусетс: Эддисон-Уэсли, ISBN  978-0-201-07392-8
• Ландау, Л.; Лифшиц, Э. (1996), Механика (3-е изд.), Оксфорд: Баттерворт-Хайнеманн, ISBN  978-0-7506-2896-9

внешняя ссылка

• «Углы Эйлера», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Углы Эйлера». MathWorld.
• Дэвид Эберли. Формулы угла Эйлера, Геометрические инструменты
• Интерактивное руководство по углам Эйлера доступно на https://www.mecademic.com/resources/Euler-angles/Euler-angles
• ЭйлераУглы – приложение для iOS для трехмерной визуализации трех вращений, связанных с углами Эйлера.
• Библиотека ориентации – «orilib», набор процедур для управления вращением / ориентацией, включая специальные инструменты для ориентации кристаллов
• Онлайн-инструмент для преобразования матриц вращения доступен на преобразователь вращения (числовое преобразование)
• Онлайн-инструмент для преобразования символьных матриц вращения (мертв, но все еще доступен из Wayback Machine ) преобразователь символьного вращения
• Вращение, отражение и смена кадра: ортогональные тензоры в вычислительной инженерной механике, IOP Publishing



2.5. Тройной интеграл в сферических координатах

До сих пор мы использовали цилиндрическую систему координат, которая, по технической

сути, представляет собой «плоскую» полярную систему + дополнительную координату «зет». Но есть задачи, где невероятно

удобны сферические координаты.

В данной системе координат точка  пространства определяется её расстоянием   («ро») от начала координат и двумя углами:
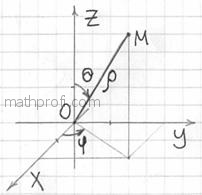
Угол  («тета») называется зенитным и отсчитывается

от положительной полуоси .

Данный угол изменяется в пределах  и

крайнему значению  соответствуют точки,

лежащие на нижней полуоси .
Угол  называется азимутальным и

отсчитывается в плоскости  против часовой стрелки. Он изменяется в пределах , иными словами, «ведёт» себя точно так же, как

полярный угол.
Таким образом, с помощью трёх координат «ро», «тета» и «фи» можно однозначно определить любую точку  пространства.  

Где используется сферическая система координат? Ну, конечно, в астрономии. Однако своё скромное применения она нашла и при

вычислении тройных интегралов:

Пример 48

Вычислить интеграл  по шару .

Решение: тот редкий случай, когда можно обойтись без чертежа. Однако я всё же втайне мечтаю, что потомки

оценят художественную ценность моих сканов:)
Тройной интеграл

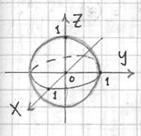
вычислим с помощью сферической системы координат. Формулы перехода к ней таковы:

При этом произведение трёх дифференциалов превращается в следующую вещь:
, где «добавка»  – это «плата» за переход.

Определим порядок обхода тела. Для этого нужно найти уравнение сферы  в сферических координатах. По формулам перехода:

, откуда следует элементарное

уравнение

Теперь смотрИте на чертёж выше и представляйте это в динамике:

– луч радара исходит из начала координат и выходит из тела через сферу :
, при этом зенитный угол

проходит все свои значения:  и

получившийся полукруг с диаметром на оси  совершает полный оборот вокруг этой оси:

В результате мы учли все точки шара, т.е. полностью обошли тело интегрирования.

Преобразуем подынтегральную функцию  и

осуществим переход к сферической системе:

Остальное дело техники:
1)
2)
3)

Ответ:

Этот тройной интеграл можно было взять и через цилиндрические координаты, но вычисления

получились бы заметно труднее. 

Когда целесообразно использовать сферическую систему координат?

Прежде всего, когда нет проблем с определением зенитного угла. Как правило, это шар и его части, шар, вложенный в

другой шар и т.п. конструкции. Кстати, шаровой сектор из Примера 46 – там этот угол прям конфетка, и я предлагаю вам

самостоятельно решить данный интеграл вторым способом:

Пример 49

Вычислить тройной интеграл  по

области, ограниченной поверхностями , с помощью сферической системы координат.

Ответы, разумеется, должны совпасть.

Следует однако заметить, что само по себе использование сферических координат ещё не означает, что решение

получится проще.

Но самое интересное только начинается:

2.6. Физические приложения тройного интеграла

2.4. Как вычислить произвольный тройной интеграл?

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин